基于遗传算法的BP神经网络的变压器故障预测

于莹++袁萍++刘晓龙

摘 要：本文是基于遗传算法的BP 神经网络对变压器的运做状况进行在线评估。实时监测变压器的运行状态以便于检修和处理。创立一个三层的神经网络，以电气试验，油色谱分析，绝缘油特性三部分對应的数据为输入层，以变压器的4种评估状态“正常状态”、“注意状态”、“异常状态”、“严重状态”作为输出层。由于变压器内部结构复杂，故障现象具有不确定性，传统分析方法有不足，通过遗传算法可以得到更好的权值和阙值，在使用BP神经网络模型对变压器的故障进行判断，该方法使判断结果更精确。

关键词：变压器；遗传算法；神经网络；状态分析

DOI：10.16640/j.cnki.37-1222/t.2017.24.186

1 变压器的重要性

变压器是电力系统中重要的设备之一，主要起到变换电压的作用，以利于功率的传输，减少电能的损失。随着电力系统传输的距离越来越长，电压等级越来越高，电网规模越来越大，电力变压器的故障率随也呈现出上升的趋势。如果电压器发生故障，会影响使电力系统运行的安全性和稳定性。甚至可能造成停电事故，而且一旦电压器损坏，购买新的变压器不仅昂贵，而且运输过程中需要等待大量的时间，运输到现场还要安装等都要消耗时间，停电的时间越久就对电力系统的威胁越严重。为使变压器运行的稳定性进一步提高，对变压器的运行状态实时监测非常重要。

2 基于遗传算法的BP神经网络的设备故障预测

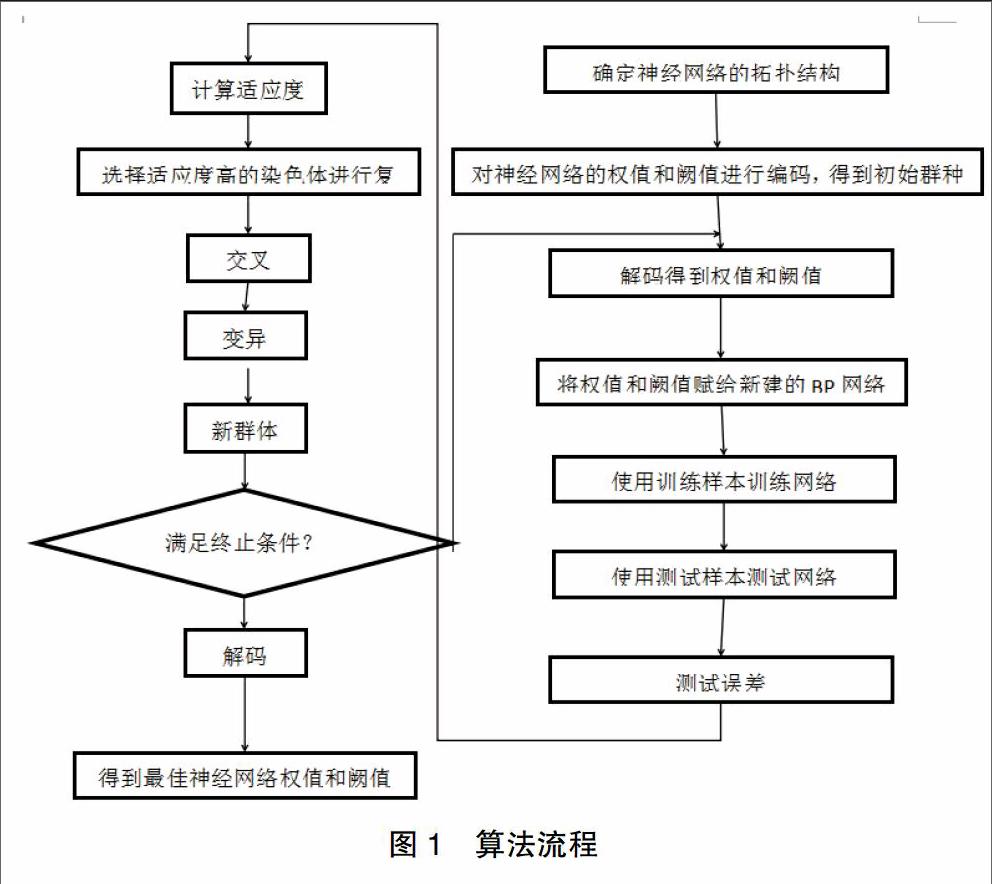
遗传算法优化BP神经网络分为：BP神经网络结构、遗传算法优化权值和阙值、BP神经网络训练及预测。神经网络的权值和阙值通过随机初始化为[-0.5，0.5]区间的随机数，这个初始化参数对网络训练的意义很大，但是又无法准确获得，对于相同的初始权重值和阙值，网络的训练结果是一样的，引入遗传算法就是为了优化最佳的权值和阙值[1]。图1是算法流程：

2.1 BP神经网络的实现

利用BP神经网络对电力变压器进行故障判断，建立三层的神经网络，以电气试验的绝缘电阻，吸收比，泄露电流，介损植，绕组直流电阻，铁芯接地电流，油色谱分析中的H2，CH4，C2H2，C2H4，C2H6，CO，CO2和绝缘油特性中的油中微水，油介质，击穿电压一共16个元素的数据为输入层。以变压器的4种评估状态“正常状态”、“注意状态”，“异常状态”，“严重状态”对应的状态数据作为输出层。同时，在神经网络为三层时，已知输入层神经元个数，可利用公式求出隐含层的神经元的个数：

n2= 2 * n1+1；

从三个大方面中采集变压器16个数据作为输入参数，变压器的4个运行状态作为输出参数。所以，n1取值为16，即输入层有16个节点，经计算隐含层有33个节点，输出层有4个节点，预测共有528个权值，132个阙值，遗传算法优化参数的个数为660。

2.2 遗传算法的实现

遗传算法优化BP神经网络使用遗传算法来优化BP神经网络的初始权值和阈值，优化后的神经网络能够更好的进行样本预测，他的实现流程是初始化群种，计算种群适应度值，从中找出最优个体，选择操作，交叉操作，变异操作，判断进化是否结束，没有结束在进行计算种群适应度值在进行一次操作[2]。

2.3 MATLAB程序实现

遗传算法和MATLAB软件的神经网络理论，遗传算法优化的谢菲尔德法变压器部分采用MATLAB编程。（神经网络算法是过程的一部分）。

网络训练是一个不断修正权值和阙值的过程，给定训练次数为1000次，训练目标为0.01，学习率为0.1。基于MATLAB具体训练代码如下：

Function err=Bpfun（x，P，T，hiddennum，P_test，T_text）

Inputnum=size（P，1）

Outputnum=size（T，1）

net=feedforwardnet（hiddenum）；

net=configure（net，P，T）

net.layers{2}.transferFcn=logsig；

net.trainParam.epochs=1000；

net.trainParam.goal=0.01；

net.trainParam.lr=0.1；

net.trainParam.show=NaN；

w1num=inputnum*hiddennum；

w2num=outputnum*hiddennum；

w1=x（1：w1num）；

B1=x（w1num+1：w1num+hiddennum）；

W2=x（w1num+hiddennum+1：w1num+hiddennum+w2num）；

B2=x（w1num+hiddennum+w2num+1：w1num+hiddennum+w2num+outputnum）；

Net.iw{1，1}=reshape（w1，hiddenum，inputnum）；

Net.iw{2，1}=reshape（w2，outputnum，hiddennum）；

（下转第208页）

（上接第203页）

Net.b{1}=reshape（B1，hiddennum，1）；

Net.b{2}=reshape（B2，outputnum，1）；

Net=train（net，P，T）；

Y=sin（net，P_test）；

err=（Y-T_test）；

此中x为一个个体的初始权值和阙值，P训练样本的输入，T训练样本的输出，P_test测试样本的输入，T_test测试样本输入，hiddennum隐含层神经元的个数，T_test测试样本的期望的输出，err预测样本的预测偏差范数。整体思想就是根据对变压器采集回来的数据为输入层，通过train进行对网络的训练，训练过程中输入的权值和阙值要是经过遗传算法进行优化过的权值和阙值，使输出结果更精确。这样，把网络训练完毕后，再输入变压器的运行时的一些数据，就可以通过神经网络的自学习功能得到想要的结果。

3 结论

采用遗传算法优化BP神经网络对变压器的运行状态进行评估，实时监控变压器的运行状态，使用遗传算法优化权值和阙值后可以对变压器评估的误差降低，该方式能精确判定变压器目前工作的4种运行状态“正常状态：设备正常温度，个状态量均在标准限值内”、“注意状态：可正常运行”，“异常状态：状态量略微超过限值，严密监测运行状态”，“严重状态：状态量严重超过标准值，应派人马上检修”。为巡检工作部署提供了良好的操作依据。

参考文献：

[1]朱瑶野.基于油中溶解气体的变压器故障预测研究[D].

[2]郁磊.MATLAB智能算法30个案例分析[D].北京：北京航空航天出版社，2015（08）.

作者简介：于莹（1982-），吉林长春人，硕士，研究方向：变电站智能化运行、新能源并网技术研究与应用。