转差频率控制的异步电动机矢量控制系统仿真
2017-12-29陈庆胜
陈庆胜
摘 要:目前矢量控制是交流电动机的先进控制方式,含有矢量变换的交流电机控制一般都称为矢量控制。异步电动机的矢量控制是交流调速的发展方向之一, 针对基于转差频率的矢量控制,设计出一种控制模型,并利用MATLA仿真软件进行了分析。结果表明,转差频率的矢量控制方式具有良好的动静态性能,有良好的实用价值。
关键词:异步电动机;转差频率;矢量控制
DOI:10.16640/j.cnki.37-1222/t.2017.24.122
1 引言
近年来,现代变流调速技术发展迅速,其动态特性已经显著的改善,在实际工业现场,交流电动机调速已经得到广泛的应用。常用的电动机机变频调速控制方法有电压频率协调控制 (即u/f比为常数)、转差频率控制、矢量控制以及直接转矩控制等[1]。其中转差频率控制技术具有结构简单、方法简便、精度高等特点。基于此,本文对转差频率矢量控制进行研究分析和仿真,并对仿真结果进行分析。
2 转差频率控制的异步电动机矢量控制的基本原理
转差频率矢量控制,如果能够保持转子磁链不变,设法改造交流电动机,对其产生转矩的规律进行改变,相当于在交流电动机上模拟直流电动机控制转矩的方法。
控制的基本方程式如下:
(2.1)
(2.2)
(2.3)
(2.4)
式中,Te为电磁转矩;P为微分算子;Lm、Lr为定子和转子的自感;Ψr为转子总磁链;ωs为转差角频率;
基本转矩方程为:
(2.5)
由公式2.4可知,控制转速的变化率,就可以提高调速的动态特性。Te作为变量,改变它的值就可以控制dω/dt。通过改变转差角频率ωs来控制Te,最终完成对电动机的转速控制,这就是转差频率矢量控制。
3 控制系统构建
矢量控制调速系统的结构模型如下图3.1。主电路采用的是SPWM电压型逆变器[2]。从图中可以看出,ω1=ωs+ω,即定子角频率=转差频率+转子角频率。转子转速发生变化是,定子的电流频率能随着一起升降,整个调速过程更为平滑。工业用的变频器通常会使用这个方案。
根据系统原理图和式(2.1)至式(2.4)进行分析,转子磁链保持不变的情况下,定子电流i1t决定电机转矩的大小(2.1),通过i1t可以计算出ωs的大小(2.4),转子总磁链Ψr可由i1m可以计算出。通过公式间的转换,在磁通大小不变的前提下,最终可以得到
4 调速系统仿真
4.1 建立仿真模型
根据系统原理图,构建本次仿真模型,分别由转速调节模块、函数运算模块、坐标变化模块等构成。通过三相交流电拖动三相异步电动机,主电路采用交-直-交电路。下面分模块进行模块构建说明。
4.2 函数运算模块
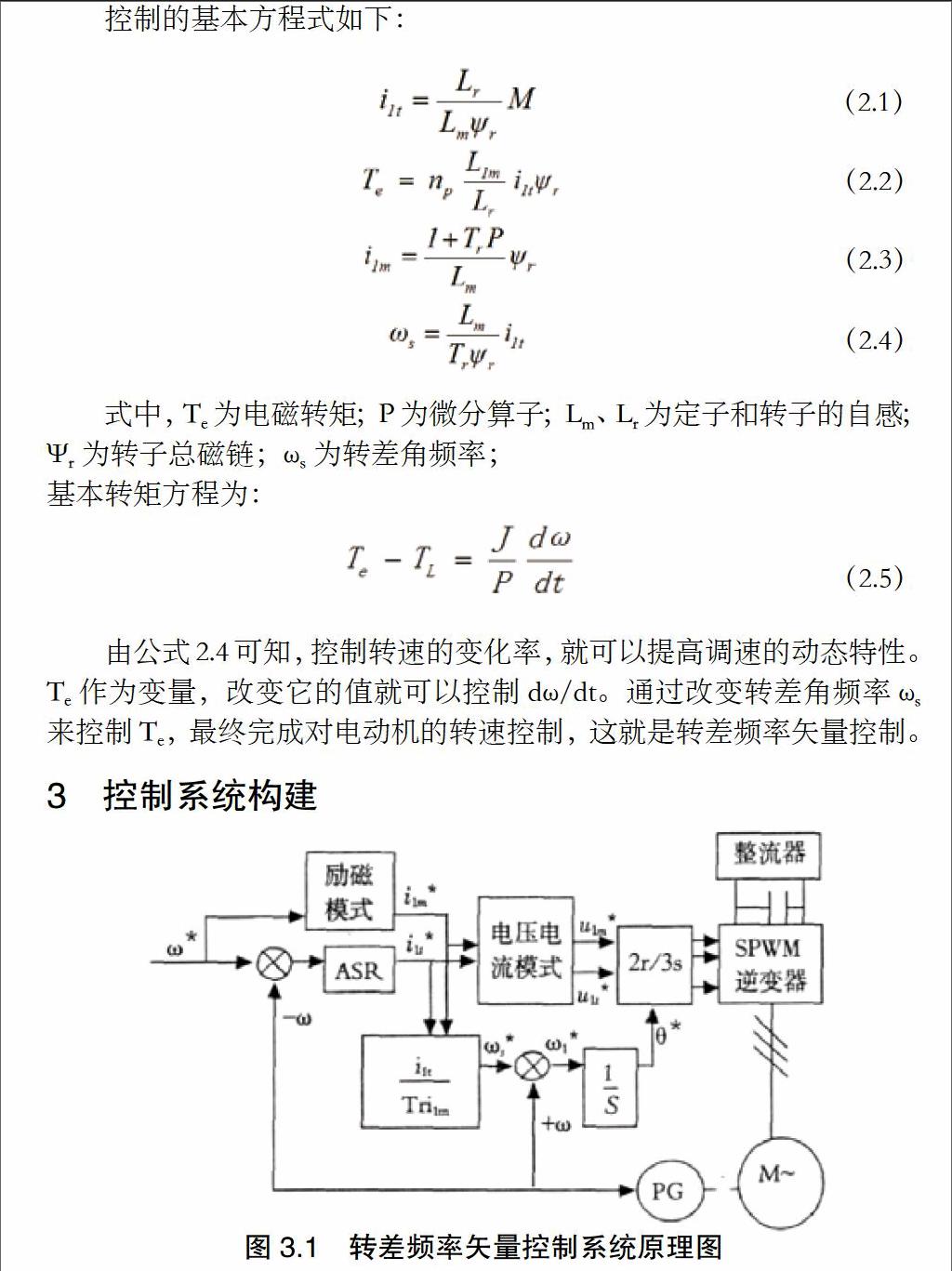
如图4.1所示,函数f(u)对电流的励磁分量进行计算得到转差角频率ωs,累加转子频率后得到算出定子频率ω1,最后根据公式转关对结果进行积分运算,得到定子电压矢量转角θ,完成函数运算。
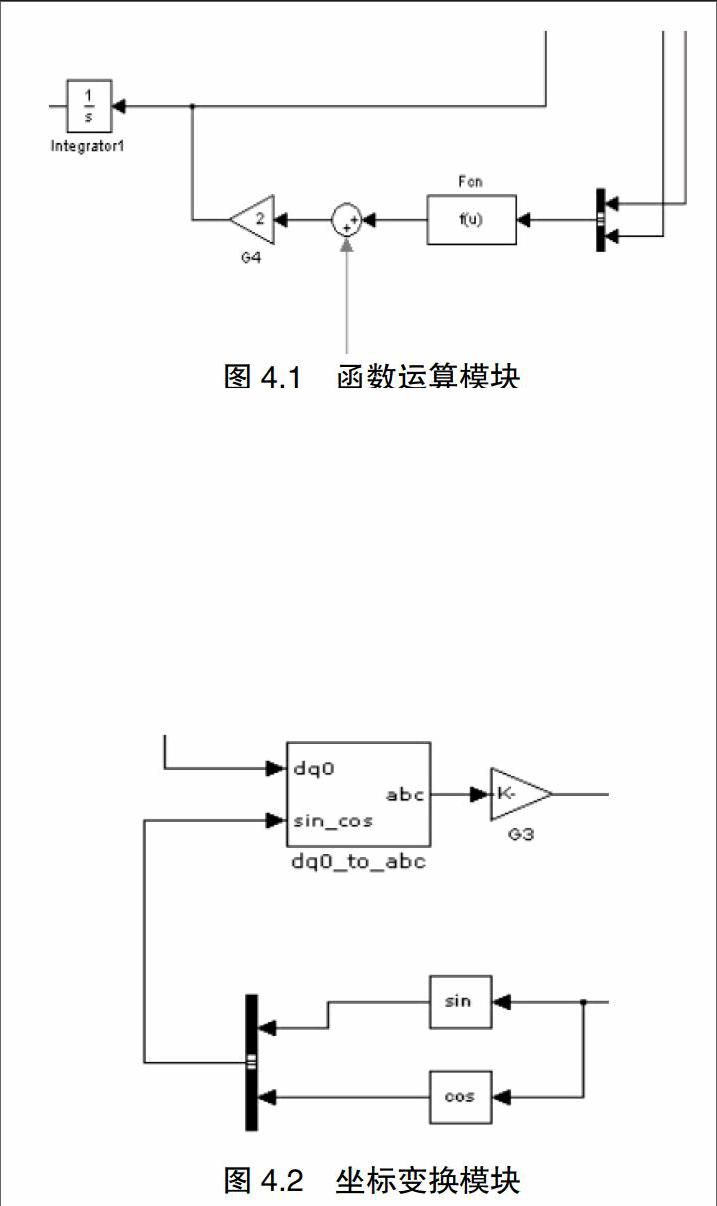
4.3 坐标变换模块
如图4.2所示,模块由G3、dq0-to-abc、sin、cos模块等构成,主要是利用Simulink中的函数公式,搭建数学变换模型。实现二相旋转坐标系到三相静止坐标的转换,dq0-to-abc的输出是PMW的三相调制信号,G3对输出信号进行衰减,使其的幅值小于1,满足输出信号的要求。衰减系数可在调试时,先断开输出,根据信号的大小计算衰减系数。
4.4 转速调节器模块
如图4.3所示,模块由放大器G1、G2、积分器和ASR构成,G2通过积分后和G1输出累加通过ASR得到,转矩电流的给定值,完成转速调节模块的作用。
系统图中的其他模块,在Simulink 模型库里都有现成模型,所以PWM模块、三相异步电动机模块、整流模块、测量模块等就不一一例举,通过将上述模块整合到一起,可建立对转差频率矢量控制系统原理图的仿真模型,完成仿真。如图5.1所示。仿真的参数表5.1所示。
5 仿真结果
在Simulink中建立仿真模型后,对系统进行仿真。在启动0.35s时加载TL=65N*m,给定环节有励磁分量im*和转子速度n*。仿真原理图如图5.1所示。
5.1 仿真过程
5.1.1 只加入比例环节
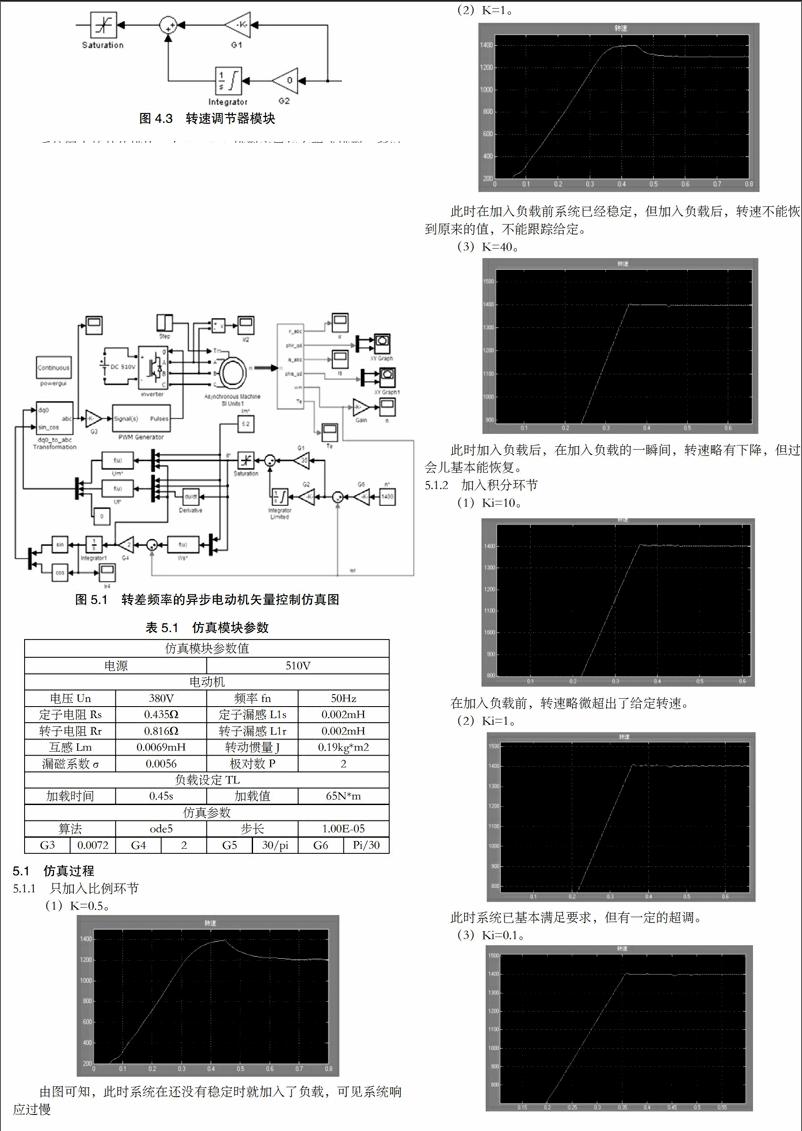
(1)K=0.5。
由图可知,此时系统在还没有稳定时就加入了负载,可见系统响应过慢
(2)K=1。
此時在加入负载前系统已经稳定,但加入负载后,转速不能恢复到原来的值,不能跟踪给定。
(3)K=40。
此时加入负载后,在加入负载的一瞬间,转速略有下降,但过一会儿基本能恢复。
5.1.2 加入积分环节
(1)Ki=10。
在加入负载前,转速略微超出了给定转速。
(2)Ki=1。
此时系统已基本满足要求,但有一定的超调。
(3)Ki=0.1。
相比于Ki=1,系统的超调量减小,且在加入负载 后输出更为平稳。可见,以满足设计要求。
从上面的调节中可以看出,比例系数K越大,系统响应速度越快,而Ki越小,超调量越小,PI调节器最终参数为K=40,Ki=0.1。
5.2 仿真结果
仿真实验最后得到了转速波形图、转矩输出波形图、输出定子三相电流波形图、输出转子三相电流波形图、转子磁链轨迹图和定子磁链轨迹图。从仿真图上可以看出,当外部转矩加载时,转矩、电流经有约1秒钟的调整,期间电流、电压均短暂下降,短暂调整后随之增加,转矩也跟着调整并恢复不变。期间转速波动的最大值约为10r/min。
另外,也图中也可以看出,电动机在刚启动时,绕组的旋转磁场的建立是不规则的,转矩的波动变化也较大,约0.2秒后,磁场、转矩、转速趋于平稳,磁场呈现规律的变化。
6 总结
本文试图通过建立转差频率矢量控制调速系统的仿真模型,对转差频率矢量控制调速系统进行仿真,仿真过程中,对比例积分环节不同的值也进行了尝试,得出了较为满意的结果。结果表明转差频率控制的矢量控制系统具有良好的静、动态控制性能。
参考文献:
[1]洪乃刚.电力电子、电机控制系统的建模和仿真[M].北京:机械工业出版社,2006.
[2]邹桂平,曾鑫.异步电动机转差频率的矢量控制仿真[J].机电工程技术,2009,38(11):19-20.
[3]陈伯时.电力拖动自动控制系统(第四版)[M].北京:机械工业出版社,2009.
[4]王会涛,钱希森,王吉校,王永民.转差频率控制的异步电动机矢量控制调速系统的研究和仿真[J].电气应用,2007,26(11):80-83.