紧扣“三个维度”有效拓展开放题的解题思路

随着素质教育和创新教育的纵深推进，数学开放题的教育价值已被越来越多的数学教师认同。开放题冲破了传统的限制，以它的开放性、灵活性、多变性给学生思维创设了更广阔的空间，有助于激发学生的创新意识，养成创新习惯，发展思维的创造性，提高学生的分析问题、解决问题的能力。

怎样提高学生解决数学开放题的能力呢？结合自己的实践经验，我认为拓展开放题的解题思路是解决开放题的金钥匙。

一、借助假设法，拓展开放题的解题思路

二、张扬学生个性，拓展开放题的解题思路

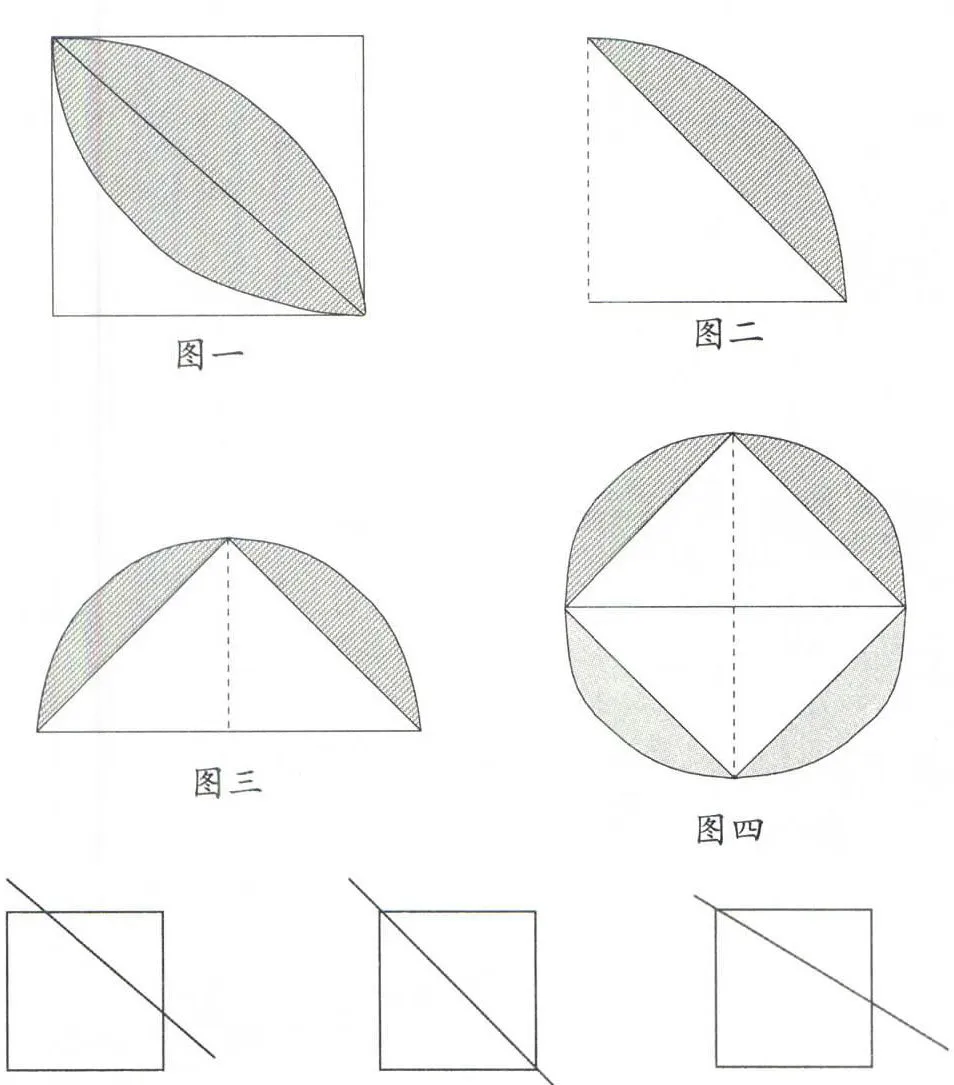
弗来登认为，每个人都有自己的数学现实，即每个人都有自己的生活、工作和思考的特定客观世界以及反映这个世界的各种数学观点、运算方法和有关知识结构。开放题教学就为孩子们提供了一个这样充分自由的环境。在一个班级里，孩子们的原有知识基础、学习习惯、学习方法、理解与感受等能力各不相同。许多孩子喜欢按自己特定的方式发展自我。这种独特的思维方式有时候是拓展开放题解题思路的金钥匙。如：六年级学完“圆的面积”之后，整理复习中有一道求阴影部分面积的图形题（见图一）。大部分学生都想到用四分之一圆的面积减掉一个直角三角形的面积后再乘2。（见图二）另一个学生则提出了这样的做法：阴影部分的面积可以看做是一个半圆的面积减去一个大三角形的面积。（见图三）我马上表扬她不仅善于观察而且善于思考。同时，鼓励同学们继续探究，看看还有什么好方法。一阵短暂地沉默后，学生们有了惊喜地发现。一位学生说：可以看做是一个大圆里画一个最大的正方形，用大圆的面积减掉正方形的面积，再除以2（见图四）；还有的想到，可以看做一个大的正方形里面画一个最大的圆。先用正方形的面积减掉圆的面积，得到空白处的面积除以2，然后用图上小正方形的面积减掉刚才求出的空白处面积……“问渠那得清如许，为有源头活水来”，就是这独特思维的源头活水焕发了强大的生命力，让我们看到了个性思维绽放的智慧火花。

三、强化动手实践，拓展开放题的解题思路

小学生心理发展的重要特点是，对新鲜的具体事物感兴趣，善于记忆具体的事实，而不善于记忆抽象的内容。大教育家陶行知提出“知行合一”的教育理念，杜威也倡导“做中学”。可见，动手实践活动正是数学知识的抽象性和学生思维的形象性之间架起的一座“桥梁”，是解决数学问题的有效途径。如：一个正方形沿着一条直线切去一个角，还剩几个角？这个问题刚出现时，孩子们会异口同声地说：“还剩三个角”。这时候不急于告知孩子们答案，可以让他们动手操作，拿出正方形剪一剪、在本上画一画。通过操作就会出现不同的答案。（如下图）原来画的方法不同得到的结果也不同。在小学数学教学过程中，教师要适当、充分地让学生亲自动手实践，调动学生的积极性，使他们体验到学习数学的快乐。同时在掌握知识的过程中，使学生的创新意识和创新潜能得到有效的发展。

四、有效利用封闭题的變式延伸，拓展开放题的解题思路

开放题的设计本身意在开发学生的解题思路，开发学生潜在的学习能力，开放性数学问题给不同层次的学生学好数学创设了机会，如果长此下去，拓展学生开放题的解题思路，会有力地发展学生的创新思维，培养学生的创新技能，提高学生的创新能力，也会让学生的个性得到自由发展。

（作者单位：抚顺市新宾满族自治县平顶山中心小学）

（责任编辑：杨强）