基于“困惑”细化设计

课堂教学是师生双边的互动过程，没有学生的积极参与，就不会有饱含生命力的课堂教学。因此，要想引导学生积极参与学习，就一定要深入研究学生，细化教学预设。

纵观小学数学教与学的过程，会发现从一年级到六年级，学生在学习的过程中会存在许许多多的思维困惑。通常的教学策略是，针对学生的思维困惑，教师反复讲解时常强调，但往往事倍功半收效甚微。因此，基于学生的思维困惑，我们努力研究如何细化教学设计，激活学生的思维和情感，创建优质、高效的课堂教学。

一、研究“差异”，巧用资源

《义务教育数学课程标准（2011年版）》要求教师要有强烈的资源意识，要努力去开发利用资源。从宏观课程的观点看，课堂中的各种因素，教学中的各种信息，都可看作是宝贵的教学资源。

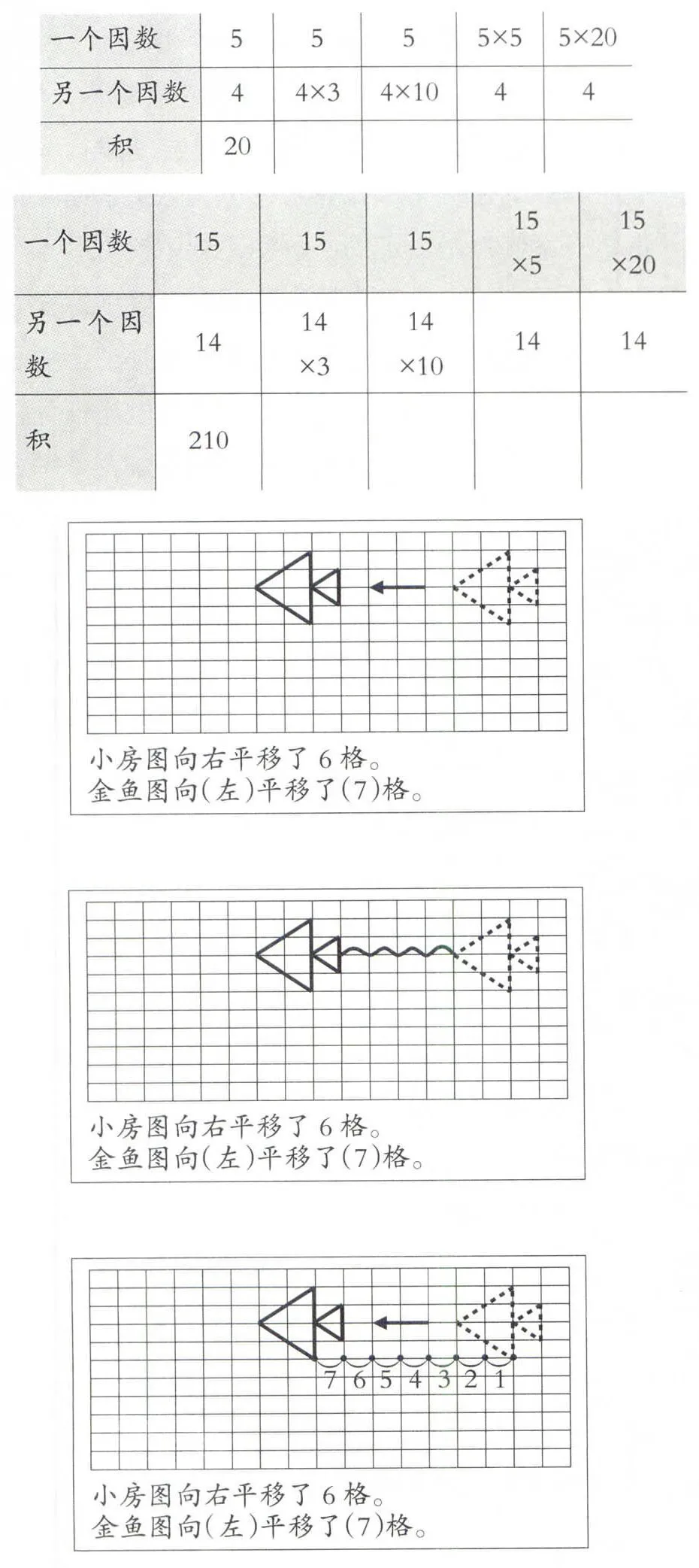
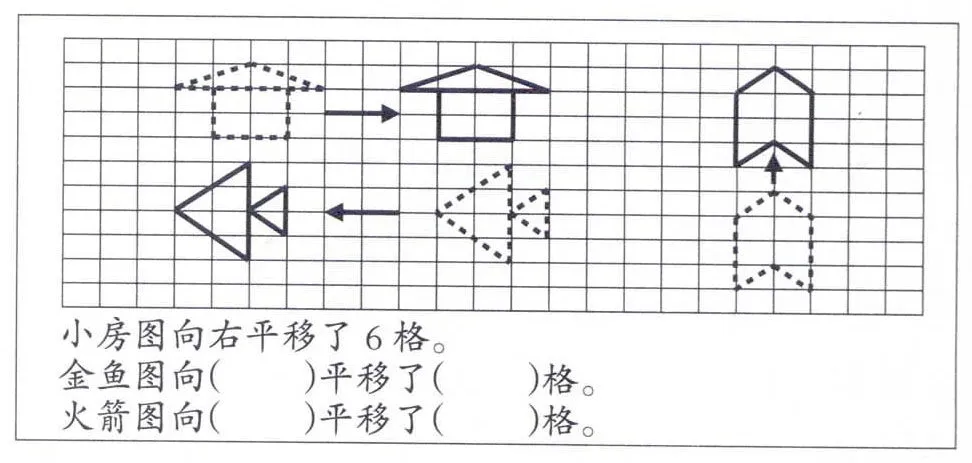
苏教版《义务教育教科书·数学》三年级教学“平移”时，平移的方向学生很容易理解，但是“1格”和“对应点”的建立则是学生学习过程中的两块“绊脚石”。特别是“1格”的建立，经老师反复讲解强调后，依然会有一部分学生数的是“点”而不是“格” ，甚至到了四年级也还会存在这样的现象。这说明，这部分学生的思维中还是没有“格”。但是，换个角度想想，大部分的孩子不是已经能够正确数格了吗，既然老师的讲解效果不好，那就让这些会数格的孩子来解释他们的数格过程，岂不是更贴近孩子们的思维。

教材例2图，金鱼图向（左）平移了（ ）格。正确答案是7格，少部分学生填8格。

师：你是怎样数出8格的，能上来数给同学们看看吗？（生1指着点数数，其余观察）

师：谁愿意来评价一下他数格的过程？

生2：老师，他数得不对，刚开始那一个点不能数，应该从后面一个点开始数1。

生3：刚开始那个点也能数，但是要数0，因为还没有开始平移。

师：那你能上来把数格的过程展示给大家看看吗？

（生上去边指边数）

师：为了让同学们看得更清楚，大家能把数格的过程表示在图上吗？

孩子们独立在图上数格，出现了不同的表示方法，有标注数字“1、2、3、……”，也有标注数字“0、1、2……”，还有标注“波浪线”的。如下图：

标注数字、画波浪线数格等方法，这些都是优生的思维成果，借助这些资源，可以生动形象地帮助其他学生建立了“一格”的概念，也使部分学生对“起点为0”有了更深层的本质的理解，同时还能让部分思维浮躁不能认真数格的孩子静下心来扎实做题，可谓是一箭三雕。再来完成火箭图，全班同学竟然没有一个数错平移格子的，效果非常显著。

二、研究“过程”，巧改数字

教材中的有些内容，表面上看，学生似乎已经掌握，其实，洞察学生的真实想法，才会发现，真正的教学目标并没有实现。因此，教师要学会深挖学生的思维过程，重组学生发出的各种信息，合理调整，扬沙捡金。

苏教版《义务教育教科书·数学》四年级下册“用计算器探索规律”，通过例1 的教学，学生探索出积的变化规律后，完成“想想做做第1题”，如下图：

本题原意是明确要求学生应用例题中发现的规律填空，以使学生进一步熟悉积的变化规律。如果完成后只是让学生交流答案，则无一出错；如果让学生说一说是怎样得到答案的，就会发现学生思维的原态大都是直接口算。

师：看最后一题，你是怎样得到400的？

生：看最后一栏，5乘20等于100，直接口算100乘4等于400就行了。

师：同他想法一样的举手。（小手如林）

师：刚刚是要求你们应用积的变化规律来思考，你们怎么没用呢？

生：老师，这题很简单，直接口算就知道结果了，根本不需要去考虑积的变化规律。

师：那你们认为，这题可以怎样改动，就能让你们想用“积的变化规律”来思考呢？

生陷入思考，几秒后，争先恐后举手：老师，我知道了，把数字改大点，比如改成15乘14，就不好口算了。

顺应学生的思维，教师改题如下：

这时，学生再来交流思维过程，就已经是自觉运用积的变化规律了。

趁热打铁，教师又抛出一题：666×667= 你能很快说出结果吗？生无语，表示不能。

教师问：如果告诉你333×667=222111，你能很快说出结果吗？学生立刻沸腾了：“老师，是4442222，第一个因数乘2，另一个因数不变，积也乘2，所以是444222！”这时，无需老师多说什么，学生已经自觉体验到积的变化规律的应用价值了。

最初完成想想做做第1題，因为数字简单，学生借助原来口算的思维水平就可知道得数，那时，学生的思维是静止的；学生积极动脑，改题再练，这时，学生的思维泛起了涟漪，对积的变化规律才开始有了兴趣；再到突遇666×667，学生表面上看似平静，其实脑中已经是暗潮汹涌，正在积极搜索题目的答案，这时，老师给出了333×667=222111，学生有了拐杖，脑中灵光一闪，立刻找到了得数。经历了这段灵动的思维体验，积的变化规律的应用价值就会在不知不觉中根植于学生的头脑里。

三、研究“症结”，巧借体验

教材中的有些题目，学生不会，无从思考。这些来自学生思维的困难就是教学研究的着力点。

苏教版《义务教育教科书·数学》四年级上册升和毫升单元里有一道题。一个洗菜池的容量，大部分学生会选择“10升”，还有部分学生无所适从，不知道如何思考。分析学生思维的症结，不难发现，之前的学习，学生只是初步建立了1升的实际意义，只是初步形成了正确估计容量比1升多些或少些的能力。如果以“1升”为参照量去判断和推测，这个参照量显然太小，学生没有将其累加至一个比较大的量的想象能力和推测能力。

学生思维的症结，仅仅看着图片听教师讲解就能解开吗，答案显然是否定的。解铃还须系铃人，孩子们只有在动手实验中自己去探究和体会，才能深刻建立“若干升”的直观感受和表象积累。于是，面对孩子们出现的不同答案和无所适从，我没有做出任何评价，而是要求他们自己想办法寻找正确答案，下节课交流。

第二天课上交流时，孩子们的发言非常真实、有趣。

生1：课本上的选择答案有5升、10升、30升。我想5升太少了，30升太多了，我就选10升，有的同学在30升上打了勾，究竟是哪个对呢，老师没说，我回家问爸爸妈妈，他们也不知道，于是我就用一个2升的瓶子装满水往池里倒，一共是13次就满了，所以大约是26升。通过测量才知道选30升更合适。

生2：我是和爸爸一起做的实验，我倒了5升水，量了一下水深3厘米，又量了水池深大约是17厘米，我推算结果大约是30升。我感觉这个实验真好玩。

生3：我用一个能装3升水的大瓶子往洗菜池里倒水，第一次倒进去，刚盖个底，我吓坏了，就这样一瓶一瓶地往里面倒，倒完第9瓶的时候，水满了，还溢出来一点，我得出洗菜池大约能装27升水。这次学习可真有趣。

生4：老师，我也认真实验了，可是我家的洗菜池容量大约是10升。

师：哦，你家的洗菜池是什么样的？

生：4是一个大的带一个小的，我测量的是那个小的，大约10升。

师：测出10升的同学举手。（约有七、八个同学）

师：结果10升，大家认为可能吗？那我们应该选择哪一个答案呢？

生：各家的洗菜池不一样，有大有小，都有可能。不过好像是大约30升的洗菜池比较多，我们就选30升吧。

只有体验过了，才会真正理解。其实，计量单位的教学，还有空间观念的形成等等都需要学生自身的操作体验和想象来支撑。这样的实验活动，无论是活动本身的强度，还是学生参与的深度都远远超过教师的讲解和示范。在这里，答案究竟是10升还是30升，已经不重要了，关键是孩子们在活动中体验，在反思中感悟，通过估计和操作结果的不断比较，逐步建立了一些比较大的量的空间感。之后再来完成一个浴缸的容量选择，孩子们通过交流、思考和想象，初步发展了借助熟悉的参照物去进行合情推理与分析的能力。

四、研究“错误”，巧设问题

错误能反映出学生认识上存在的偏差，反映出学生的学习困难所在，以及行为习惯、情感态度等状态。所以，教师要做有心人，要及时收集、整理一些典型错误。当学习相关内容时，这些宝贵的错误资源就可以帮助教师更好地从学生实际出发进行教学。

在刚刚学习“三位数除以整十数”时，部分学生出错率特别高，因为之前学习的都是除数是一位数的除法，现在除数变成了两位数，学生不適应。如700÷50=95，借助除法竖式帮助学生分析错误原因：在十位商9是因为错把除数50当成了5。针对这部分思维还不够清晰的学生，教师可以设计如下思考题，帮助学生理清思路、提升能力。

它的商可能是几位数？是怎样想的？

什么情况商是一位数？什么情况商是两位数？

这题的商最大是几？最小呢？

如果商是9，被除数最大是几？最小呢？如果商是12呢？

计算除数是整十数的除法，你认为要注意什么？

实践表明，这种激活思维、展开过程的提升练习，能帮助学生反思问题、明晰思路，能更好地促进学生数学理解的深度建构。

（作者单位：江苏省运河师范附属小学北校）

（责任编辑：杨强）