基于多周期多品种多目标的生产分布式布局遗传算法研究

李道国，徐益标

（1.杭州电子科技大学 信息工程学院；2.杭州电子科技大学 管理学院，浙江 杭州 310018）

基于多周期多品种多目标的生产分布式布局遗传算法研究

李道国1，徐益标2

（1.杭州电子科技大学 信息工程学院；2.杭州电子科技大学 管理学院，浙江 杭州 310018）

市场需求逐渐从小品种、大批量向多品种、变批量转变，现有的工艺原则布局以及成组原则布局的柔性不够，不能适应多变的生产需求，针对不足，文章提出以各种机器能力之间距离最小的分布式布局模型和以物料搬运成本最小为目标的分布式布局模型，并结合两者的特点，对两个目标函数进行标准化处理，构建了一个满足多周期、多变生产需求的多目标分布式布局模型。设计了相应的遗传算法，通过一个示例验证了模型及算法的可行性。

遗传算法；分布式布局；多目标优化

一、引言

现在制造业市场需求变化快，产品种类多样化、生命周期短，制造企业的生产方式逐渐从少品种、大批量向多品种、变批量转变。在这种情况下，传统适合大批量、多品种的车间布局形式比如：工艺原则布局、产品原则布局等，不能很好的应对不断变化的生产需求[1]。

分布式布局如图1（b），是由Montreuil等人于1991年提出[2]，通过将原本集群的具有相同功能的机器，战略性的分布于整个生产车间，从而缩短了不同功能的机器之间的距离，有利于快速高效的构造新的制造单元，降低物料处理成本，从而应对不断变化的生产需求。Benjafaar等人研究表明这种分解与分配确实能大大提高在多变生产环境下车间作业的工作效率[3]。分布式布局如图1所示。

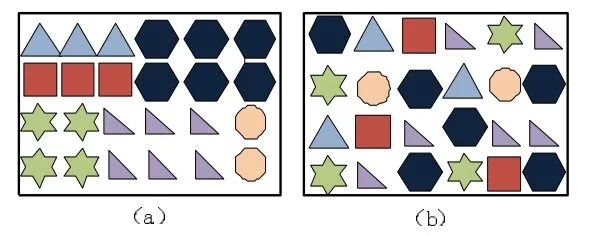
图1 布局对比图

目前国内对于分布式布局的研究不是很多，对于车间分布式布局的研究主要集中在国外。montreuil等人研究了基于机器的分布式布局[4]，baykasoglu提出了基于设备加工能力的分布式布局[5]，并通过模拟仿真对基于能力的分布式布局方式进行验证，证明了其可行性[6]。但是大部分分布式布局一般都是基于已知的产品种类、工艺以及产量从而确定布局。但是现实情况是未来的需求难以预测[7]，只考虑当前周期的需求则需要不断重构布局以适应下一周期的生产需求[8]。本文针对现有研究的不足，以最小化搬运距离以及成本为目标，提出了一种基于设备加工能力的分布式布局的方案，适应多个周期不同的生产需求，并与传统的分布式布局以及每期重构布。

二、问题描述及模型构建

基于加工能力的分布式布局是将m台机器分布于车间中，所有机器总计拥有r种加工能力，每一种机器都拥有若干种加工能力，在布局过程中不单单需要考虑机器在车间内的分布，而且需要考虑各种加工能力如何分布，产品如何选择适合的机器来加工，对此本文考虑，以各个不存在加工能力Rj的位置到存在加工能力Rj的距离最小为目标，以适应多变的生产需求[9]，同时考虑当前周期的生产需求，以物流成本最小为目标，构建一个多目标模型，使得多个周期总物流费用最小。

本文研究的问题是各个机器在车间内的分布，一般只考虑机器相对位置距离和物料搬运费用，根据问题本文做出如下假设：①车间整体空间形状规则，为矩形空间，开始点为左上角，结束点为右下角。②机器设备的形状，大小尺寸等进行简化，均考虑成大小相同的矩形。③机器分布于车间，车间规划为如图2所示的样子，每个机器占据一个固定的区域位置。④为了简化模型，不考虑物料在每一块区域内部的运输问题。⑤不考虑物料流通路径，各个相邻位置之间的距离设定为1。

（一）以距离最短为目标的布局模型

由于每个周期内产品的种类、批量和加工工艺都会发生变化，不能预测之后几个周期的产品需求。所以本文考虑产品生产过程中无论下一工序需要何种加工能力，该加工能力都能在其附近。

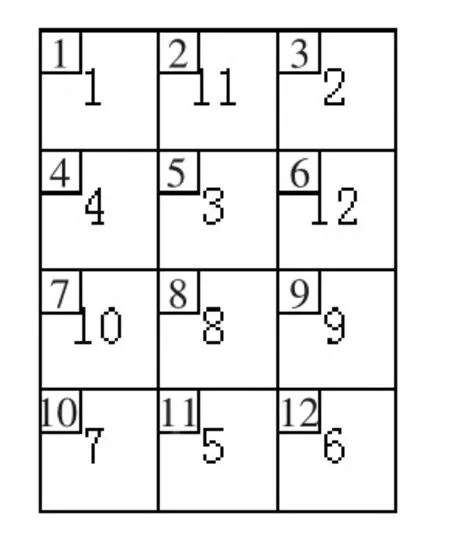
图2 车间设备布图

图3 加工能力1的分布图

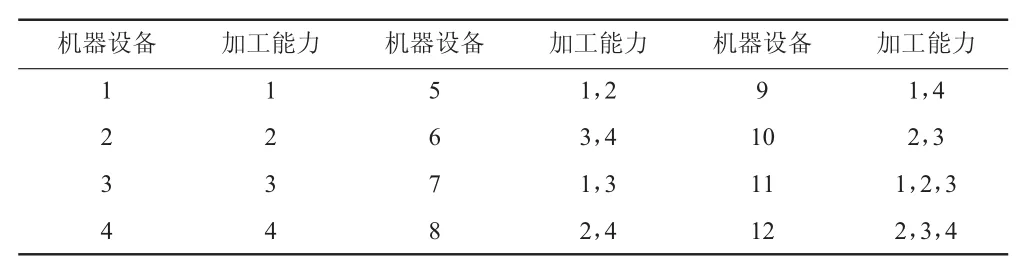
表1 机器加工能力表

表1是机器与加工能力的对应表，图2是车间布局图，左上角位置的数字表示位置编号，中间的数字表示机器编号。图3表示加工能力1在车间中的分布情况，1表示该位置存在该种加工能力，0表示不存在该种加工能力 ，由图可知加工能力 1分布于位置 1、2、9、10、11，加工能力不存在的位置为 3、4、5、6、7、8、12。各个不存在能力 1的位置到存在能力1的位置的最小距离即1+1+1+1+1+1+1=7。因此模型的目标函数设定为：

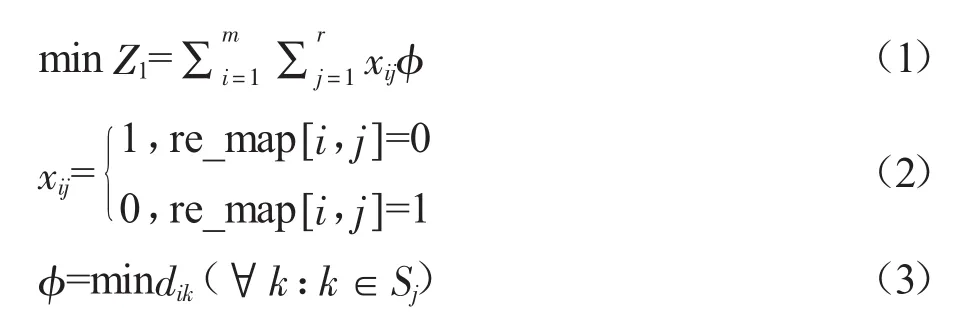
其中各个符号的意义如下：re_map[i，j]表示加工能力j是否存在于位置i，如果存在则等于1，不存在则等于 0，dik表示位置i到位置k的距离，Sj表示存在加工能力j的位置的集合。

（二）以成本为目标函数的布局模型

以距离为目标的布局模型，可以适应多变的生产需求，在每个周期的生产过程中都不会产生较高的物流费用，但也不是每个周期中最优的布局，因此以当前周期的物流成本最小也是本文所考虑的目标之一，模型如下：

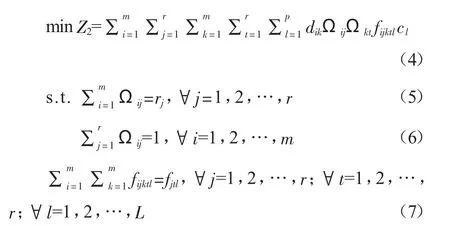
其中Ωij表示加工能力j是否存在于位置i，如果存在则等于1，不存在则等于0；dik表示位置i到位置k的距离；fijktl表示产品l的加工工艺中是否有从加工能力j到加工能力t的过程，并且该过程是否选择设备i以及设备k，如果是则为该过程的物流量，不是则为0；cl表示产品l的单位物流成本；rj表示表示拥有加工能力j的机器的数量；L表示表示产品种类数。

约束（5）和（6）保证了每个机器只能被分配在一个位置上并且每个位置也只能被一个机器占据，一旦位置数超过子部门的个数在保证最优的情况下将利用零物流量和零重新布置费用的虚拟部门来解决两者间数量上的差异。约束（7）保证产品l在具有加工能力j，t的机器i，k之间的物流量和其总的物流量相等。

（三）标准化处理

因为本文构建的目标函数有两个，属于多目标优化问题，求解多目标优化其实就是求解帕累托最优解的问题，根据实际情况求出一个令人满意的解，由于两个目标函数具有不同的量纲，所以需要对其进行标准化处理[10]，采用min-max标准化处理，也称为离差标准化，是对原始数据的线性变换，使结果值映射到[0-1]之间。转换函数如下：

最终目标函数模型为：

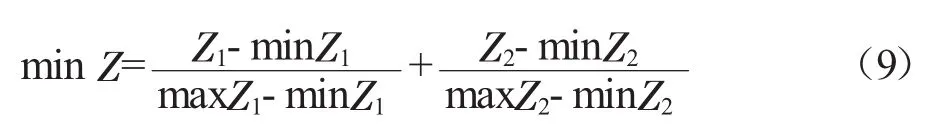
三、模型求解

本文选择使用遗传算法来对分布式布局问题进行求解，通过合理的参数设置更好的求得满意的解。基本步骤如下：

步骤1：初始化种群，采用随机生成的方式生成初始种群。

步骤2：染色体编码，编码是遗传算法成功的首要问题，排序问题一般使用符号编码，对机器进行编号，表示如下：[M1，M2，M5，M4，M3]。M1 在 1 位置，M2在 2位置，M5在 3位置，M4在 4 位置，M3在5位置。

步骤3：选择，本文采用顺序选择的方法，其将选择概率固定化。首先按适应值大小对个体进行排序，接着定义最好的个体的选择概率为q，排序后的第j个个体的选择概率为：

其中NP为种群个数，对于最小化问题来说，最好的个体也就是适应值最小的个体，目标函数可以直接作为适应值进行计算，保证了优秀个体的选择概率。

步骤4：染色体交叉，采用部分交叉策略，由于在交叉过程中会产生非法编码，所以需要化解冲突，具体如图4所示，染色体A，B交叉之后，染色体A中3，2，0发生重复，染色体B中 5，6，7重复，因此需要将染色体A中未交叉部分中的重复的基因进行替换，分别为3换成7，2换成6，0换成5。

步骤5：变异、变异是为了避免算法早熟，陷入局部最优解，本文变异方法为随机选择染色体中的一个基因，并且随机插入到染色体中的某一个位置。

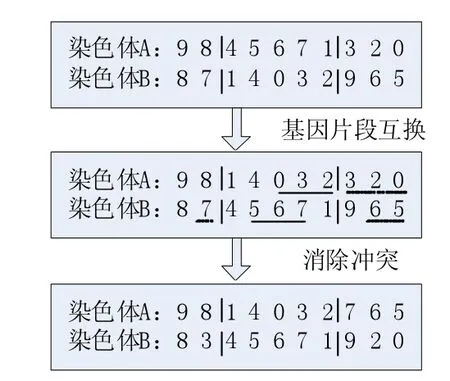
图4 交叉过程示意图

步骤6：终止，算法合理的终止条件可以提升算法的性能，本文采用两个终止条件，一是当算法达到指定的迭代次数之后终止，二是当算法结果在指定代数之后未曾优化停止算法。

四、实例分析

车间现有24台机器，整个车间的布局为4*6的结构，已知本周期的需要生产的产品种类，相应的工艺路线和各个产品的单位物流成本，如表2所示，以及各个机器设备所具备的加工能力如表3所示。假定之后四个周期的生产需求随机生成，并且每个周期的重构费用为500。

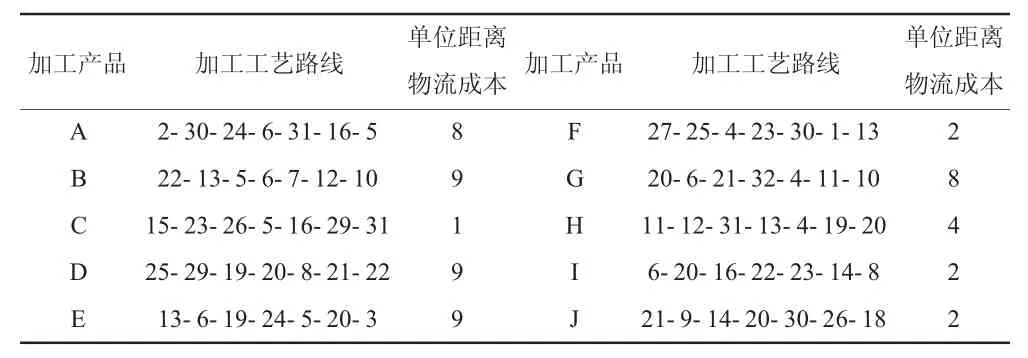
表2 生产信息表

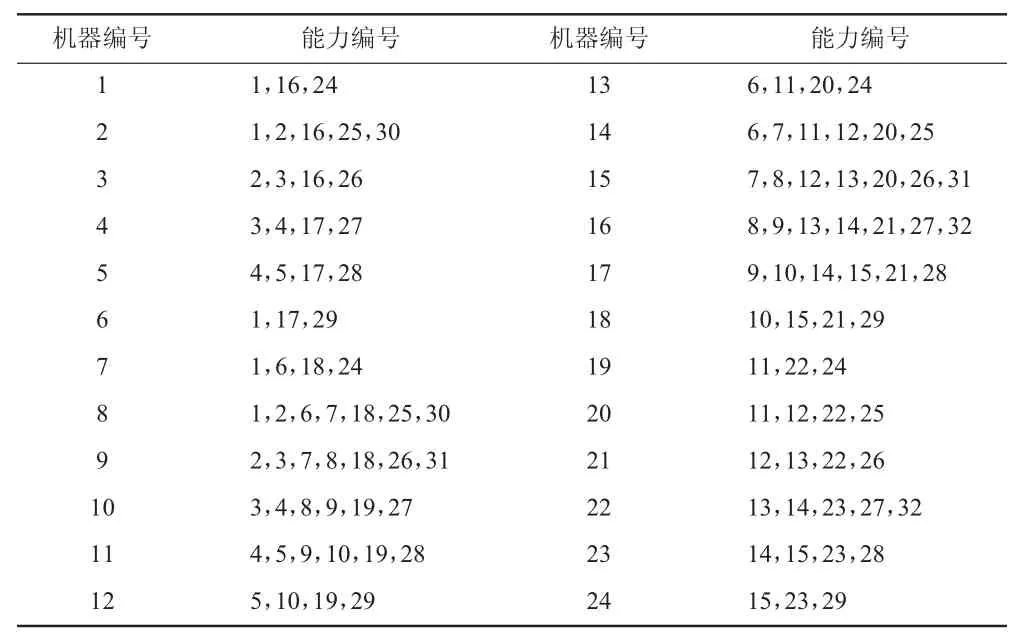
表3 机器能力对应表

为证明本文提出的分布式布局方法的正确性，将本文与传统的分布式布局的方法（模型1）以及重构的分布式（模型2）进行比较。通过算法得到的结果如表4所示。从数据中可以得知，以根据功能之间总的距离最短为目标的分布式布局方法与本文的多目标方法相比，只是在第一周期的物流费用有明显差距，其余4个周期的数据相差不大，总物流费用传统分布式模型略高于本文模型。虽然重构式布局每个周期的物料搬运成本均低于本文模型，但是每个周期都重构而会产生大量的重构费用，导致总费用远远大于本文模型。

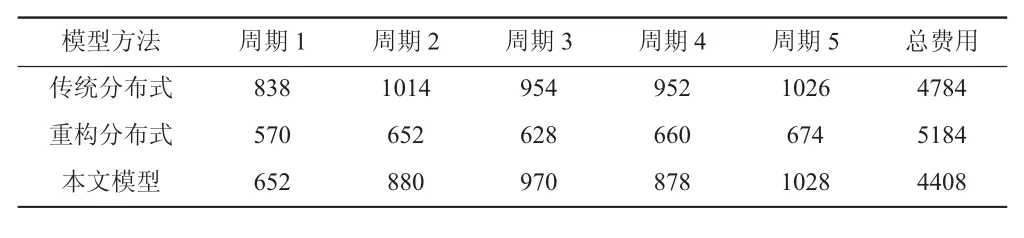
表4 不同方法的比较

最终结果证明将模型1与模型2进行合并，形成多目标函数的合理性。模型保留了传统分布式布局方法应对多变的生产需求的能力，使每个周期的物流成本不会因需求的变动而大幅波动，也避免了重构布局时产生的大量的重构费用。

五、结束语

本文针对生产需求变化过快导致的生产车间布局不能及时响应的问题，实现了以机器各能力之间距离最短以及物流成本最小化为目标函数的多目标优化问题的遗传算法，希望为多品种、变批量的制造企业的车间布局提供一种解决方案。研究还有许多不足之处，例如只考虑了各个机器之间的相对位置关系，而忽略了具体车间以及机器的尺寸，以及未充分考虑机器设备之间的相互关系等，这都有待于进一步研究。

[1]锁小红，刘战强，2007.制造系统设备布局的建模理论与求解方法[J].计算机集成制造系统（10）：1941-1951.

[2]Montreuil B，Venkatadri U，Lefranc-ois P.Holographic layout of manufacturing systems.In：19th IIE systems integration conference，October（1991）.

[3]Benjafaar S.，Sheikhzadeh M.Design of flexible plant layouts.IIE Transactions，2000，32：309-322.

[4]Montreuil B.，Venkatadri U.，Lefrancois P.（1991）Holographic layout of manufacturing systems.In 19th IIE Systems Integration Conference，Orlando，Florida，USA，pp.1-13.

[7]李聪波，马辉杰，李玲玲，等，2015.面向不确定性的再制造车间设施动态布局方法[J].计算机集成制造系统（11）：2901-2011.

[8]陶俐言，聂清，王志锋，等，2014.面向变批量生产的制造单元构建方法[J].计算机集成制造系统（10）：2411-2418.

[10]余世根，鲁建厦，2010.基于GA的固定约束条件下多目标车间设备布局问题研究[J].浙江工业大学学报（4）：401-405.

F273

A

1004-2768（2017）11-0115-04

2017-09-05

李道国（1965-），男，浙江杭州人，杭州电子科技大学信息工程学院教授，研究方向：电子商务、模式识别与人工智能；徐益标（1992-），男，浙江绍兴人，杭州电子科技大学管理学院硕士研究生，研究方向:生产计划与控制。徐益标为通讯作者。

M 校对：R）