基于最小熵解卷积-变分模态分解和优化支持向量机的滚动轴承故障诊断方法

姚成玉 来博文 陈东宁 孙 飞 吕世君

1.燕山大学河北省工业计算机控制工程重点实验室，秦皇岛，0660042.燕山大学河北省重型机械流体动力传输与控制重点实验室，秦皇岛，0660043.先进锻压成形技术与科学教育部重点实验室(燕山大学)，秦皇岛，066004

基于最小熵解卷积-变分模态分解和优化支持向量机的滚动轴承故障诊断方法

姚成玉1来博文1陈东宁2，3孙 飞2,3吕世君2,3

1.燕山大学河北省工业计算机控制工程重点实验室，秦皇岛，0660042.燕山大学河北省重型机械流体动力传输与控制重点实验室，秦皇岛，0660043.先进锻压成形技术与科学教育部重点实验室(燕山大学)，秦皇岛，066004

提出了一种基于最小熵解卷积和变分模态分解以及模糊近似熵的故障特征提取方法，并采用优化支持向量机对故障进行识别分类。首先利用最小熵解卷积方法降低噪声干扰并增强故障信号中故障特征信息，进而对降噪后的信号进行变分模态分解，并利用模糊近似熵量化变分模态分解后包含故障特征信息的模态分量以构建特征向量，之后通过采用扩展粒子群算法优化惩罚因子和核函数参数的支持向量机，对故障样本训练并完成故障识别分类。将所提方法应用于滚动轴承不同损伤程度、不同故障部位的实验数据，验证了该方法的有效性。与基于局部均值分解的特征提取方法相对比，结果表明所提方法可以更精确地提取出滚动轴承故障特征，并能够更准确地完成不同故障的识别；通过与基于网格寻优算法优化的支持向量机方法和基于扩展粒子群优化的最小二乘支持向量机方法相对比，结果表明所提方法具有更好的分类性能，能达到更好的诊断效果。

故障诊断；变分模态分解；最小熵解卷积；模糊近似熵；支持向量机

0 引言

机械故障诊断技术是现代化机械系统能够安全和高效稳定运转的关键。机械故障诊断技术主要包括信号预处理、特征提取和状态模式识别等步骤[1-2]。

故障特征提取是机械故障诊断技术的核心部分，它对整个诊断过程的计算效率和整个诊断系统的精确度都有很大影响。机械振动信号具有非线性、非平稳的特性，相对于时域分析法和频域分析法，时频域分析法更加适用于机械设备中产生的非平稳复杂信号，是故障诊断领域一种应用最广泛的方法，常用的时频域分析法有小波变换[3]、经验模式分解(empirical mode decomposition, EMD)[4]和局部均值分解(local mean decomposition, LMD)[5]等。但是，小波分解有一定局限性；EMD和LMD具有端点效应以及不同模态之间存在混叠的不足，这会导致分解结果中有虚假分量产生，从而影响到特征提取的效果。DRAGOMIRETSKIY等[6]提出了变分模态分解(variational mode decomposition, VMD)方法，这一种新的信号估计方法与EMD和LMD的递归模式不同，它是一种非递归信号分解方法，预先假设每个模态分量都存在一个中心频率以此来确定每个分量。VMD方法相比于传统递归模式分解方法具有坚实的理论基础，并且抗噪性更好，VMD方法的端点效应和模态混叠现象要远小于EMD和LMD的端点效应和模态混叠现象，从而可以更好地提取出机械振动信号不同频带下的故障特征。然而，机械设备正常运转时其工况具有复杂多变的特点，产生的振动信号容易受到强背景噪声、采集设备以及采集信号传输设备的影响，故障信息会因此而不容易被观察到，当对采集的机械故障振动信号直接采用VMD分解时，得到的结果会受到噪声的影响而导致某些分量的故障特征不明显。因此，为了增强所采集原始振动信号的有效信噪比并突出故障特征信息，对原始信号进行降噪是一个不可或缺的过程[7]。对机械信号降噪通常采用非线性降噪方法，主要有小波降噪、卡尔曼滤波、形态学去噪[8]等。但是，这些降噪方法虽然能降低噪声的干扰，但不能明显地增强机械信号中故障冲击信息。最小熵解卷积(minimum entropy deconvolution, MED)[9-10]方法通过搜索出一组最佳的滤波器系数，使经过逆滤波器输出信号的峭度最大化、熵值最小，突出信号中的脉冲特性[11]，由于故障信号中故障信息主要以脉冲形式存在，所以最小熵解卷积的特性更适用于增强机械信号中的故障信息。SAWALHI等[12]首次将MED方法应用于机械故障诊断中，使用MED对振动信号进行降噪并突出信号中的振动冲击成分，以突出故障特征信息；BARSZCZ等[13]把MED应用在检测和诊断风力涡轮机滚动轴承缺陷性的故障中。本文提出采用MED方法对采集到的机械故障信号进行预处理，降低噪声影响并增强故障特征信息，并结合VMD分解将信号分解为多个分量，从而更有效地提取出机械故障信号中各个频带中的故障特征。

支持向量机(support vector machine, SVM)是建立在统计学习理论的VC维理论和结构风险最小原理基础上的一种模式识别方法[14]，它拥有非常优秀的非线性分类能力，所以，SVM在小样本、非线性及高维模式识别中都具有不错的效果。文献[15]采用非线性流形学习，提取机电系统中存在故障的特征，利用SVM识别机电系统的故障类型。文献[16]用双树复小波变换，提取能量熵作为特征向量，利用SVM实现滚动轴承故障诊断。文献[17]利用峭度因子、方差、波形因子作为特征参量提取故障信息，应用SVM算法进行故障诊断。由于SVM需要严格的核函数及其参数调整，其分类结果会受到核函数及其参数的影响，然而传统SVM参数寻优方法、网格参数寻优法存在效率较低、搜索能力较差并且难以准确找到最优参数的不足，基于此，本文提出采用扩展粒子群优化(extended particle swarm optimization, EPSO)算法[18-19]对SVM参数进行寻优，该方法具有更佳的寻优性能，从而能够更准确地搜索到SVM最佳参数。

综上，本文拟从特征提取方面，采用MED和VMD分解相结合的方法提取机械故障信号的特征，然后利用优化支持向量机进行故障识别，最后，通过不同故障部位、故障损伤程度的滚动轴承故障信号数据验证本文方法的有效性。

1 基于MED-VMD的故障特征提取方法

1.1 最小熵解卷积方法

如果一个系统的输入x(k)是一个较为离散的尖脉冲序列，则可认为x(k)系统中结构性信息较多，由于x(k)是脉冲序列，所以其秩序性较好，熵值比较小。当输入x(k)经过一个线性系统h(n)后，其输出s(k)以卷积的形式表达为

s(k)=x(k)*h(n)

(1)

x(k)在经过h(n)后，其系统信息较之前会变得混乱，结构性特征会减少，因而其熵值会变大。解卷积其实就是设定一个合适的L阶的逆滤波器g(l)，s(k)经这个逆滤波器滤波后，使其输出y(k)尽可能地还原出x(k)，数学表达式可写作：

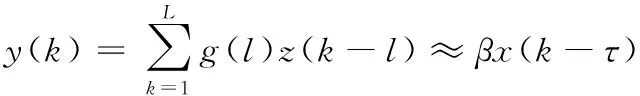
(2)

经过逆滤波器后使输出y(k)的峭度最大化，即结构性的脉冲信息增多，信息成分更有秩序，从而使熵值最小，这也是该方法被称为最小熵解卷积的原因。以目标函数法(objective function method,OFM)作为实现最小熵解卷积的基本方法，以k阶累积量作为盲解卷积过程的目标函数，表达式为

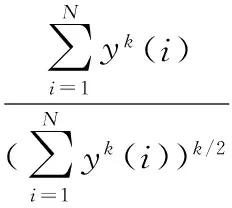
(3)

一般情况下k>2，在大多数实际应用中，k=4最为常用。由于设计的最优逆滤波器g(l)需要使滤波后的信号熵值尽可能地小，故对目标函数求导令其为零，通过式(2)可求得

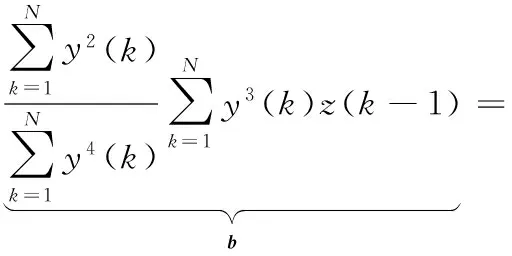
(4)

式(4)用矩阵的形式可以写为

b=Ag

(5)

式中，b为逆滤波器输入信号与输出信号之间的互相关矩阵；A为输入信号的Toeplitz自相关矩阵，g为逆滤波器必要参数组成的列向量。

可以看出，MED方法可以说是一个搜寻最优滤波器的过程，其算法流程如下：

(1)对FIR滤波器参数g(0)进行初始化设置，通常情况下设置为时延滤波器，即[0 1 0 … 0]，求出输入信号的Toeplitz自相关矩阵。

(2)根据式(2)，通过已有信号z(l)与g(k)计算输出信号y(k)，k为循环次数。求出式(4)中的b(k+1)，通过公式g(k+1)=A-1b(k+1)求解滤波器参数，更新g(k+1)。

(3)计算循环误差：

(6)

(4)将求得的误差与设定好的阈值相对比，如果得到的误差大于设定的阈值，则返回步骤(2)，循环直到误差小于设定的阈值结束，最终得到滤波器参数ge。

(5)根据式(2)，通过已有信号z(l)和步骤(4)求得FIR滤波器参数ge求ye。ye为原系统的输入x(k)的近似。

根据MED原理可知：MED方法通过不断搜索，得到一组最佳的滤波器系数，使经过逆滤波器输出信号的峭度最大化，熵值最小。在上述算法流程中，通过比较输入输出信号的目标函数大小即式(6)计算循环误差，并与预设阈值比较，作为循环终止的条件。因此，滤波器初始参数设置、循环次数和设定的误差阈值影响着MED方法的效果。

1.2 变分模态分解

变分模态分解的目的是将输入信号f(t)分解成多个模态分量信号uk，每一个模态具有有限带宽，并且都紧密地围绕在其中心频率ωk周围，要准确估计每个IMF分量的带宽，计算过程如下。

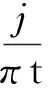
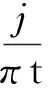
通过计算解调信号梯度的二范数的平方来估计带宽，受约束的变分问题如下：

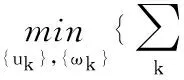
(7)

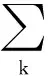
引入二次惩罚项α和拉格朗日函数λ来解决重构无约束问题。引入α能够增强重构保真度，尤其是在有高斯噪声的信号中，拉格朗日乘数能够增强约束条件的严格性，引入α和λ后的拉格朗日表达式如下：

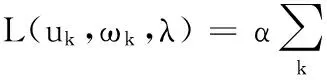
(8)

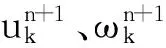
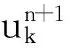
(9)

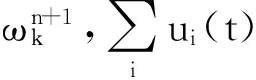
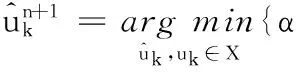
(10)

在式(10)中，将第一项中的变量ω替换为ω-ωk，最后可求二次优化问题的解为

(11)

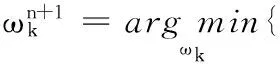
(12)

同理将最小值取值问题转换到频域得

(13)

通过式(13)求得中心频率为

(14)

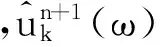
1.3 基于模糊近似熵构建特征向量

将模糊近似熵(fuzzy approximate entropy, fApEn)引入Zadeh的模糊集概念中，采用模糊函数界定向量间的相似性，克服了近似熵和样本熵算法中存在的不足。本文采用模糊近似熵量化提取故障特征，流程如图1所示，算法过程如下。

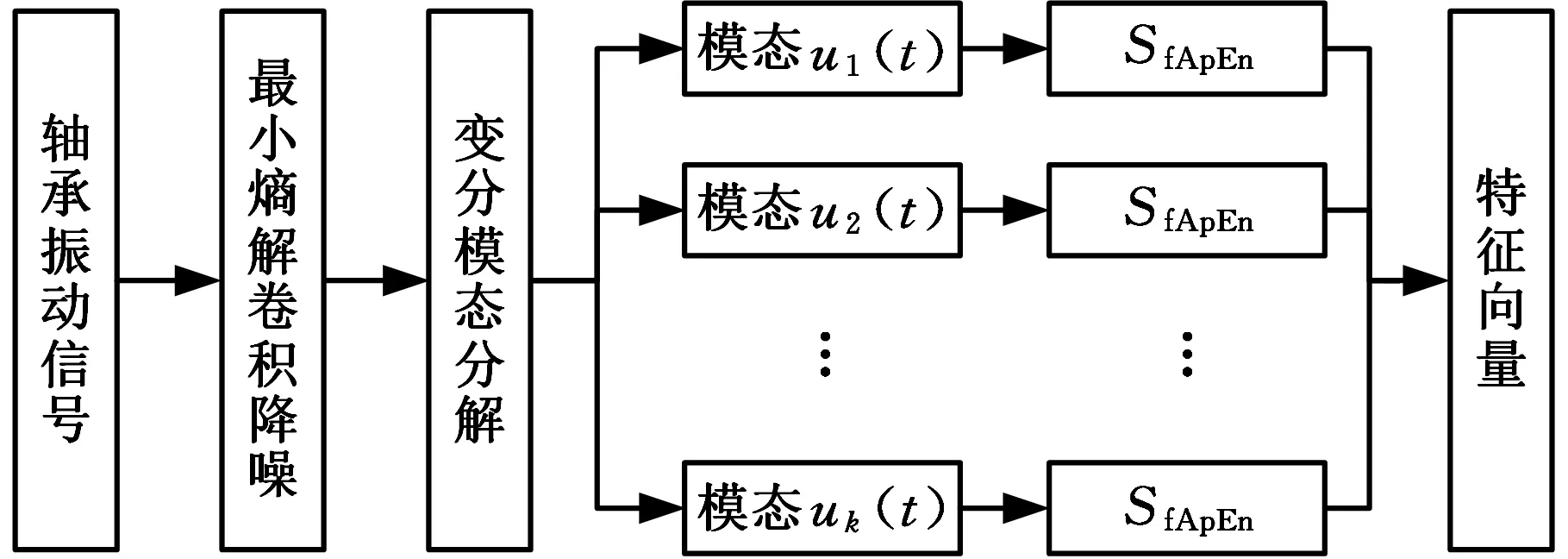
图1 构建特征向量流程图Fig.1 Flow chart of construction of feature vectors

已知一个时间序列x(i)，其中i=1,2，…，N，x(i)为x(i)第i点数据值，N为数据长度，模糊近似熵算法步骤如下：

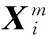
(15)

(16)

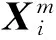
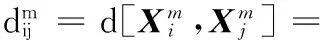
(17)

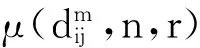
(18)

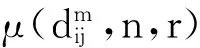
(19)

定义φm为

(20)

同样，定义m+1维φm+1为

(21)

最后，定义时间序列x(i)的模糊近似熵为

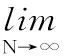
(22)

对于有限长的时间序列，SfApEn(m,n,r)可通过其统计值SfApEn(m,n,r,N)估计得到：

SfApEn(m,n,r,N)=lnφm(n,r)-lnφm+1(n,r)

(23)

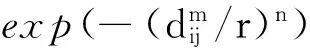
2 基于优化支持向量机的故障识别方法

故障识别方法关系到故障识别的准确率，上文研究了特征提取的方法，并以模糊近似熵构建了特征向量，需要采用一个有效的故障识别方法对其进行分类识别。支持向量机是一种优秀的机器学习方法，通过采用合适的核函数可以将非线性分类空间的数据投射到高维线性分类空间之中，具有强大的非线性分类能力，为此本文采用支持向量机对故障特征向量进行处理，从而完成不同故障类型的识别。但是支持向量机的惩罚因子和核函数参数选择关系到识别正确率，传统的网格寻优方法效率较低、搜索能力较差并且难以准确找到最优参数。为此，本文采用扩展粒子群优化(EPSO)算法对参数进行寻优，EPSO算法是为了克服标准粒子群算法的早熟问题而提出的一种改进粒子群算法，相较于广泛使用的标准粒子群算法，该算法具有更佳的寻优性能，能够准确地搜索到影响支持向量机效果的最优参数。

2.1 支持向量机

假设存在两种线性可分的数据集：(xi,yi),i=1,2，…,n,xi∈Rd,yi∈{1,-1}，线性判别函数的表达式写作f(x)=w·x+b，最优分类面H可以通过转化成约束优化问题进行求取：

(24)

为此，定义如下拉格朗日函数：

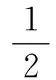
(25)

式中，w为最优分类面H的法向量；αi为拉格朗日乘子，αi≥0；ξ为松弛因子。

为求式(25)的最小值，分别对w、b求偏导，并令其等于零，得

(26)

利用拉格朗日优化方法，依据沃尔夫(Wolfe)的对偶理论可以把上述分类问题表示为如下凸二次规划寻优的对偶问题：

(27)

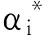
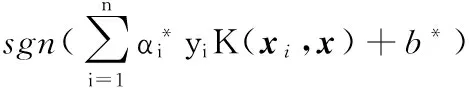
(28)

本文选用径向基函数作为支持向量机的核函数，构造的SVM判别函数为

(29)

其中，n个支持向量xi可以确定RBF核函数的中心位置，n为中心的数目，σ为尺度参数。

本文选用LIBSVM(library for support vector machines)工具箱对样本进行训练并分类，LIBSVM采用序列最小优化算法(sequential minimal optimization, SMO)对SVM模型中凸二次规划寻优的对偶问题进行求解，并且LIBSVM采用了收缩和缓存技术，在计算速度和性能上都有不错的表现。

2.2 扩展粒子群算法

扩展粒子群算法是为了克服粒子群算法的早熟问题而提出的一种改进粒子群算法。扩展粒子群算法把标准粒子群算法中粒子只受到其他粒子吸引的形式，扩展为粒子会被比自身适应值优的粒子所吸引，并且被比自身适应值劣的粒子所排斥，在引力和斥力合力的作用下对速度和位置更新。粒子间引斥力规则定义如下。

如果第j个粒子的适应度比第i个粒子的适应度好，则粒子j对粒子i引力为pjk(t)-xik(t)。

如果粒子B(i)={j|f(Pj)≤f(Xi),∀j∈S}，j∈B(i)，则B(i)集合存放历史最优适应值比粒子i适应值优的粒子。

如果第j个粒子的适应度比第i个粒子的适应度差，则粒子j对粒子i斥力为-(pjk(t)-xik(t))。

如果粒子W(i)={j|f(Pj)>f(Xi),∀j∈S}，j∈W(i)，则W(i)集合存放历史最优适应值比粒子i适应值劣的粒子。

其中，集合B(i)和W(i)的元素个数分别以|B(i)|和|W(i)|来表示。

EPSO的速度和位置更新方程为

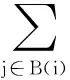
(30)

xid(t+1)=xid(t)+vid(t+1)

(31)

式中，vid(t)为第t代粒子i第d维速度；xid(t)为第t代粒子i的第d维位置；pjd(t)为第t代粒子j的个体最优解的第d维位置；w为惯性权重；c1、c2为加速常数；r1、r2为(0, 1)区间互相独立的随机数。

2.3 基于EPSO优化的支持向量机

本文LIBSVM方法选用径向基函数作为核函数，径向基函数的参数σ和SVM中惩罚因子C的选取直接影响SVM的分类精度，参数σ即式(29)中的σ，参数C即式(27)中的C。LIBSVM自带传统网格搜索法对参数C和σ寻优，对网格内所有的参数组合进行尝试，筛选出最优参数，但是该方法效率不高。由于网格搜索法中C、σ需要预设范围，只能取有限离散值组合，所以搜索到的结果极可能不是最优，如果先用粗粒度搜索然后再用细粒度搜索，搜索出的值也很可能是局部最优解，有可能较单次的网格搜索稍好，但最终结果仍不是全局最优解。EPSO算法作为一种高效的搜索算法，可以克服以上网格搜索算法的不足，基于此，本文采用EPSO算法对LIBSVM的参数C、σ寻优。

在EPSO算法对LIBSVM参数寻优过程中，一种参数组合训练一组数据集所得的训练模型，由于无测试集，需要交叉验证评估此训练模型的预测正确率，正确率最高的参数组合即为寻优结果。

EPSO优化LIBSVM参数的步骤如下：

(1)初始化种群。在搜索空间中随机初始化代表参数C、σ粒子的速度向量和位置向量，及空间中每个粒子在[vmin,vmax]和[xmin,xmax]区间内随机产生的每一维速度和位置分量；计算粒子的适应值即交叉验证的结果，在开始时粒子历史最优位置pi(0)等于各粒子的初始位置，进化代数t=0。

(2)根据式(30)计算粒子的下一代速度。

(3)根据式(31)计算粒子的下一代位置。

(4)计算粒子适应值并更新每一粒子的历史最优位置pi。

(5)判断是否达到终止条件，如果达到，即运算终止，输出寻优结果；若不满足，进化代数t←t+1，返回步骤(2)。

(6)输出最优参数C、σ组合。

3 实例分析

本文采用美国凯斯西储(Case Western Reserve)大学所采集的滚动轴承故障数据作为故障诊断实验数据。采取驱动端滚动轴承实验数据进行分析，该滚动轴承型号是SKF6205-2RS，有9个滚动体，采样频率为12 kHz。

3.1 特征提取

选用电机转速为1797 r/min、损伤点直径为0.1778 mm的内圈故障信号数据进行分析，数据长度为2048，采用LMD方法对此内圈故障信号进行分解，并对分解后的分量做包络分析，结果如图2所示。

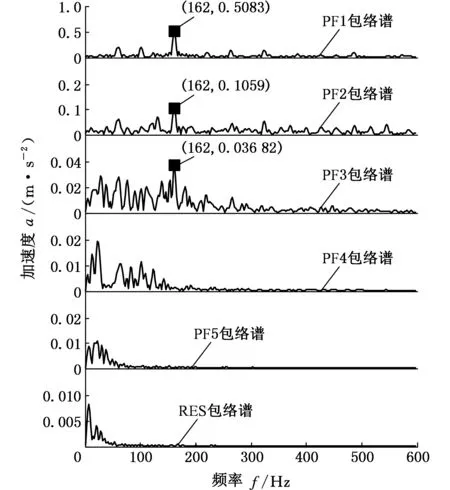
图2 内圈故障信号LMD分解包络图Fig.2 Envelop diagrams of fault signals of inner ring decomposed by LMD

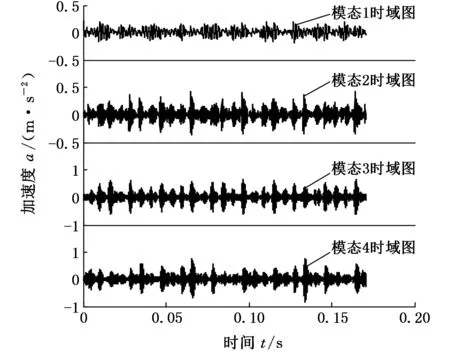
图3 内圈故障信号VMD分解时域图Fig.3 Time domain diagrams of fault signals of inner ing decomposed by VMD

对内圈故障信号进行VMD分解。VMD算法中，模态个数选择K=4，参数α选择默认值2000，为了保证信号分解的保真度，τ选择0.3。内圈故障信号分解后的时域图见图3。对分解的每个模态进行包络分析，得到VMD分解后各模态的包络谱，结果如图4所示。

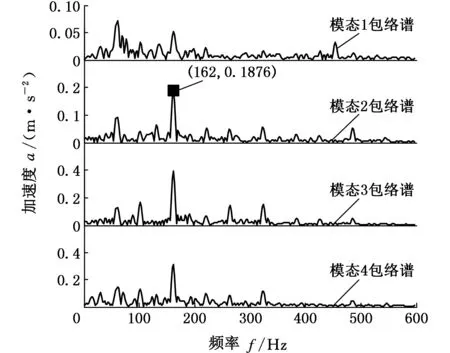
图4 内圈故障信号VMD分解包络图Fig.4 Envelop diagrams of fault signals of inner ring decomposed by VMD

从图2和图4中可以看出，内圈故障信号经LMD自适应分解为5个PF分量和一个残留分量，只有前3个分量包含内圈故障特征频率162 Hz，而VMD分解后虽然第1个模态中包含的故障特征频率不是很明显，但是4个模态全部包含内圈故障特征频率162 Hz，由此可以看出VMD分解后的每个模态携带的故障特征信息要优于LMD分解后各分量携带的特征信息。

虽然对故障信号直接使用VMD方法分解后，每个模态分量都包含故障特征频率，然而，一些模态分量的故障特征频率处谱线幅值没有最突出，这是由于滚动轴承在运行过程中会存在噪声和低频信息的影响，使故障特征信息不能很明显地突出。最小熵解卷积方法使经过逆滤波器输出信号的峭度最大化、熵值最小，突出信号中的脉冲特性。由于滚动轴承故障信号中故障信息主要以脉冲形式存在，所以最小熵解卷积的特性很适用于增强滚动轴承信号中的故障信息。对相同内圈故障信号采用MED方法处理，MED的滤波器点数设为40，最大循环次数为30，误差为0.01。滤波前后的内圈故障信号的时域波形如图5、图6所示。

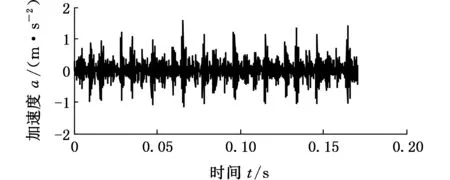
图5 内圈故障原始时域波形Fig.5 Time domain waveforms of original fault signals of inner ring

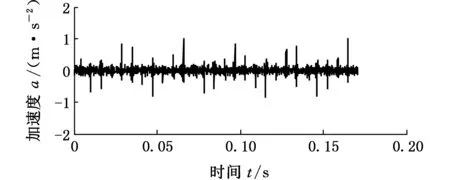
图6 内圈故障信号MED降噪后时域波形Fig.6 Time domain waveforms of fault signals of inner ring after MED denoising

从图5和图6可以看出，内圈故障信号经过MED降噪后，其低频噪声少了许多，信号中的振动冲击成分更加凸显，而这些冲击成分即为故障特征信息。对经过MED方法滤波后的信号进行VMD分解，对分解的每个模态进行包络分析，得到VMD分解后各模态的包络谱，结果如图7所示。

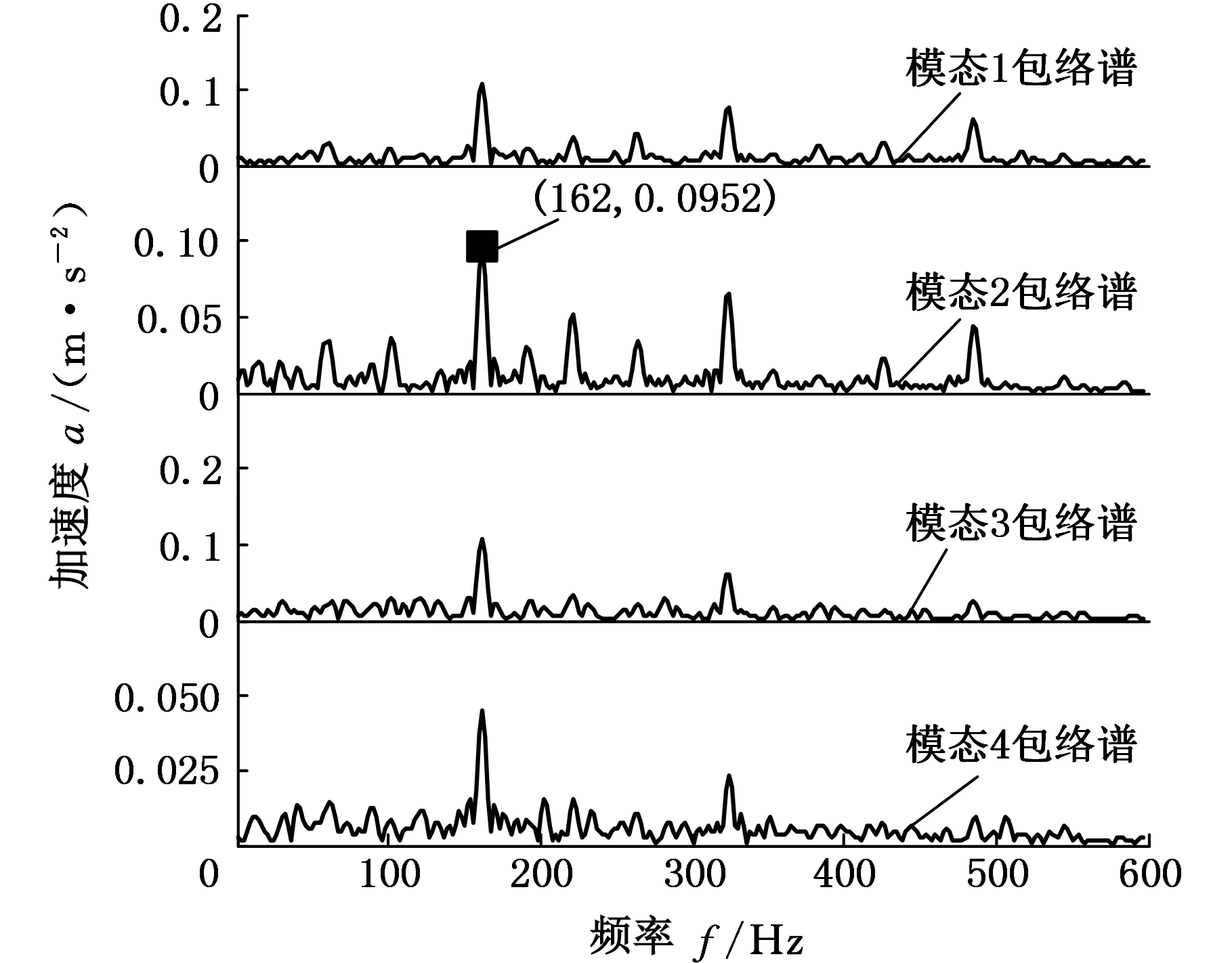
图7 内圈故障MED降噪后VMD分解的包络谱Fig.7 Envelop spectrum of inner ring fault after MED denoising decomposed by VMD

由图4和图7对比可以看出，在经过MED降噪后，模态1的特征频率谱线由之前不太凸显变得明显，所有4个模态的低频成分都要减少很多，内圈故障特征频率可以很清晰地观察到，表明故障信号在经过MED降噪后，再通过VMD分解进行特征提取的方法要更为有效。

3.2 不同故障部位故障诊断

选择正常滚动轴承与故障点直径为0.3556 mm的不同故障类型数据进行分析，随机选取1750 r/min转速下，正常状态、内圈故障、外圈故障和滚动体故障各60组数据，其中随机选取40组作为已知故障样本，20组作为待诊断样本，采样点个数均取1024。对信号采用MED-VMD分解，求取4个分量的模糊近似熵，构造的特征向量为T=(SfApEn1,SfApEn2,SfApEn3,SfApEn4)，由训练样本构成的特征向量如表1所示，其中类型1、2、3、4分别代表滚动轴承正常状态、内圈故障、外圈故障和滚动体故障。剩下20组作为测试样本。

将上述40组训练样本输入基于EPSO参数优化的LIBSVM中进行训练，将剩下20组数据作为待识别故障样本输入训练好的模型中进行识别，EPSO初始参数c1、c2为1.5、1.7，种群大小为20，迭代次数为200次，寻得最优参数C=11.05、σ=1.52，诊断结果如图8、图9所示。

为了对比分析，采用传统的网格参数寻优方法对LIBSVM的参数进行优化，为了更好地进行网格寻优搜索，设置C的范围为[-30,30]，σ的范围为[-10,10]，寻得最优参数C=1，σ=1.6，网格寻优过程的三维图和诊断结果如图10和图11所示。

为了对比分析LIBSVM分类的性能，下面使用EPSO优化最小二乘支持向量机(least squares support vector machine, LSSVM)惩罚因子C和RBF核函数参数σ，数据与上述一致，寻得最优参数C=0.1、σ=0.01，分类结果如图12所示。

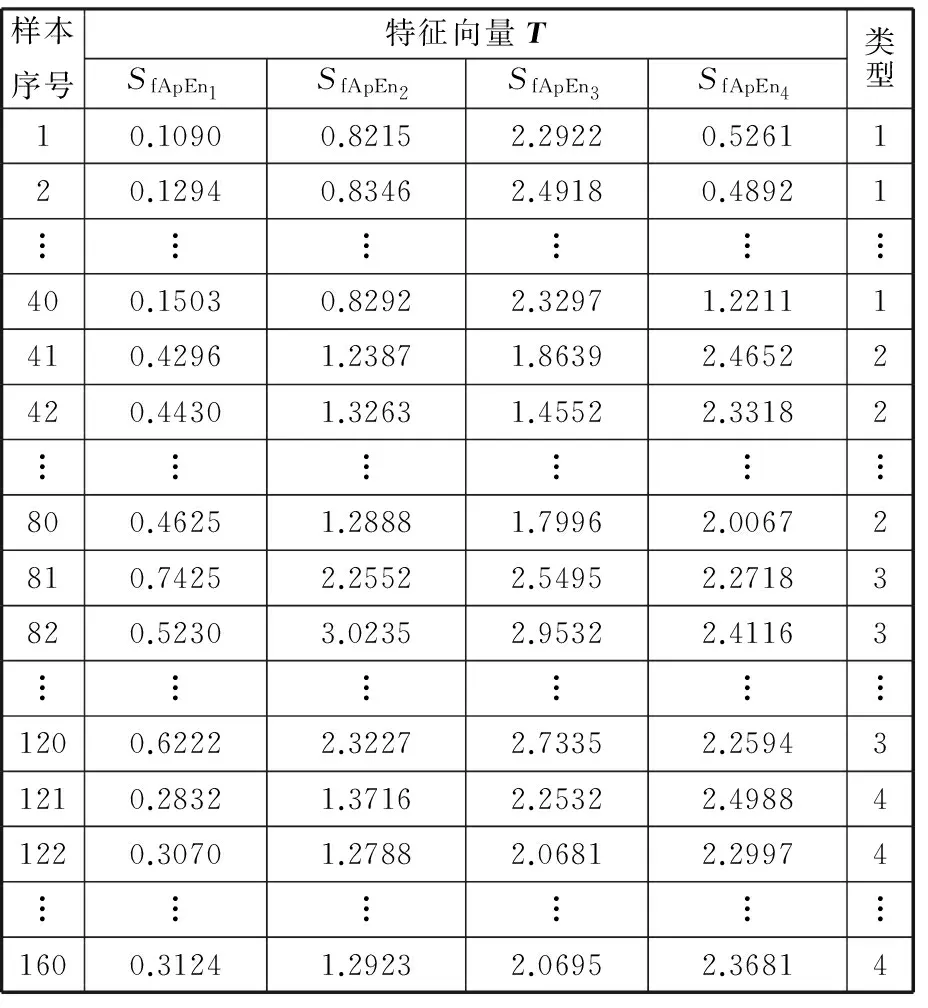
表1 由训练样本构成的特征向量

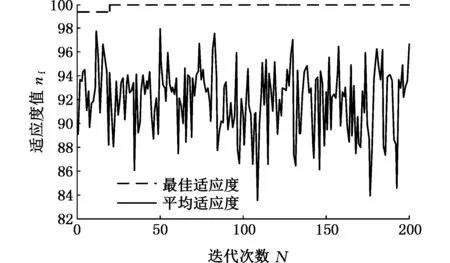
图8 EPSO优化LIBSVM适应度图Fig.8 Fitness diagram of LIBSVM optimized by EPSO

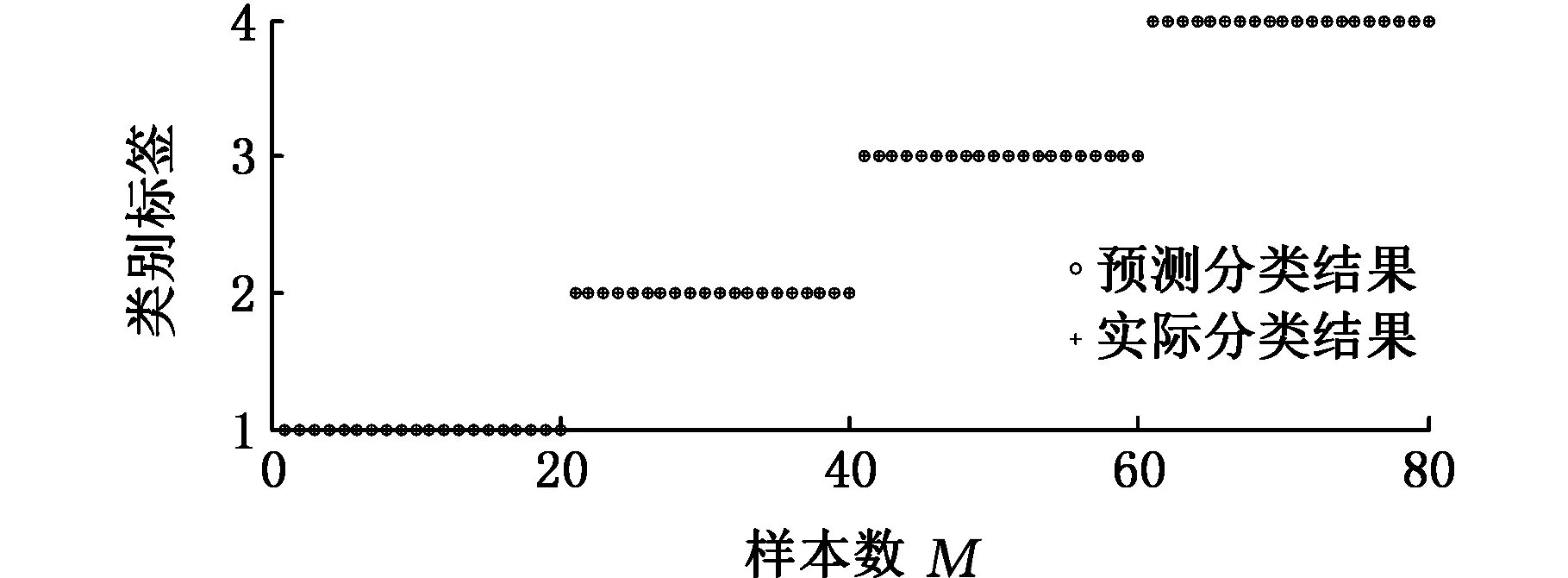
图9 EPSO优化LIBSVM参数故障诊断结果Fig.9 Fault diagnosis results of LIBVM parameters optimized by EPSO

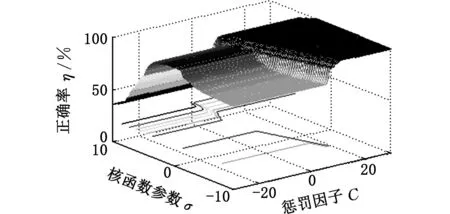
图10 网格参数寻优三维视图Fig.10 The 3D view of parameters optimized by grid search

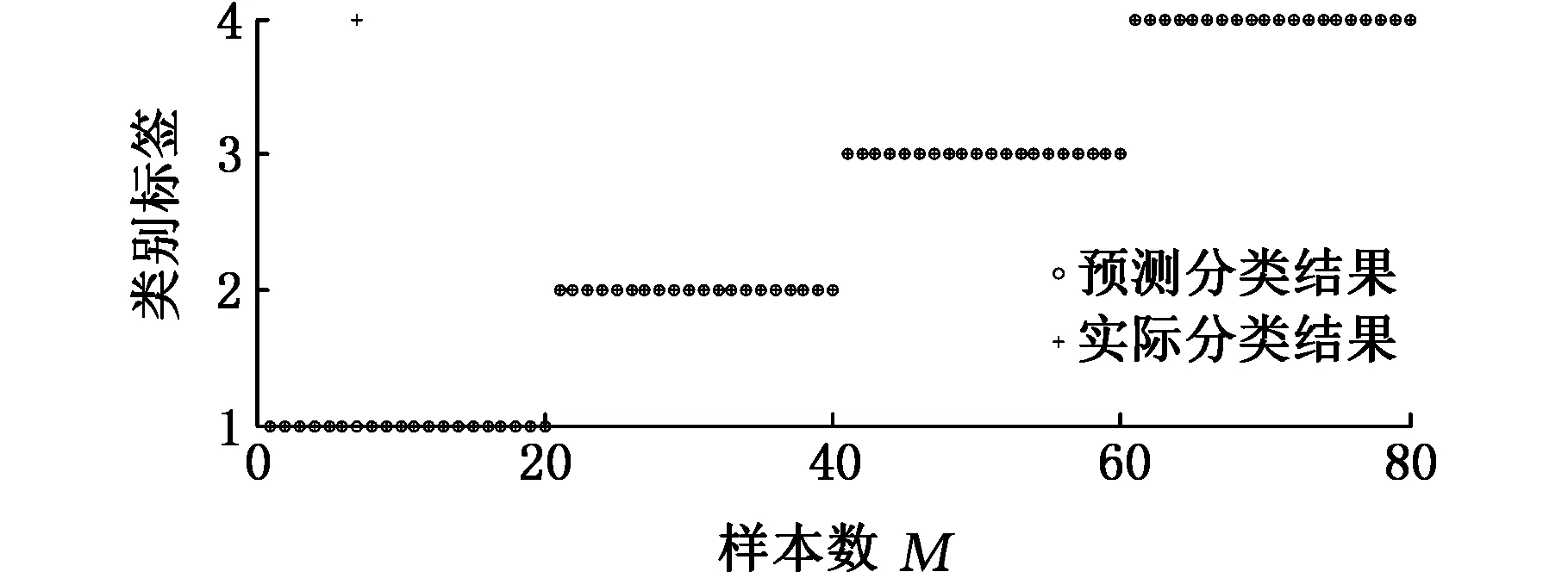
图11 网格参数寻优故障诊断结果Fig.11 Fault diagnosis results of parameters optimized by grid search

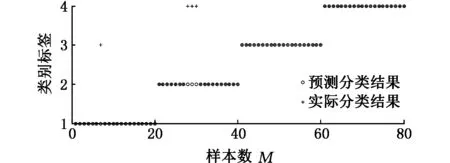
图12 EPSO优化LSSVM参数故障诊断结果Fig.12 Fault diagnosis results of LSSVM parameters optimized by EPSO

表2为三种识别方法诊断的结果，通过表2可以看到，网格寻优和EPSO寻优的结果对比，网格寻优得到的分类结果比EPSO寻优的结果正确率稍低，并且网格寻优的运行时间要比EPSO寻优的时间多出很多，从而说明了，网格寻优方法效率较低、运算量较大、寻得的参数不一定为最优值，EPSO相对于网格寻优在搜寻LIBSVM参数方面效率更高，寻得的参数更佳。EPSO-LSSVM相较于EPSO-LIBSVM正确率要低，原因可能由于在LSSVM中，平方损失函数没有经过正则化，这会导致支持向量的误判，从而会在模型上产生一定误差，因此会导致LSSVM的预测准确率比LIBSVM的预测准确率低。另外，由于LIBSVM选用SMO算法作为求解的最优模型，而LSSVM选用最小二乘算法作为求解的最优模型，所以LIBSVM运算时间要比LSSVM运算时间少很多。从而可以验证EPSO优化LIBSVM参数的故障识别方法是一种更有效的故障诊断方法。

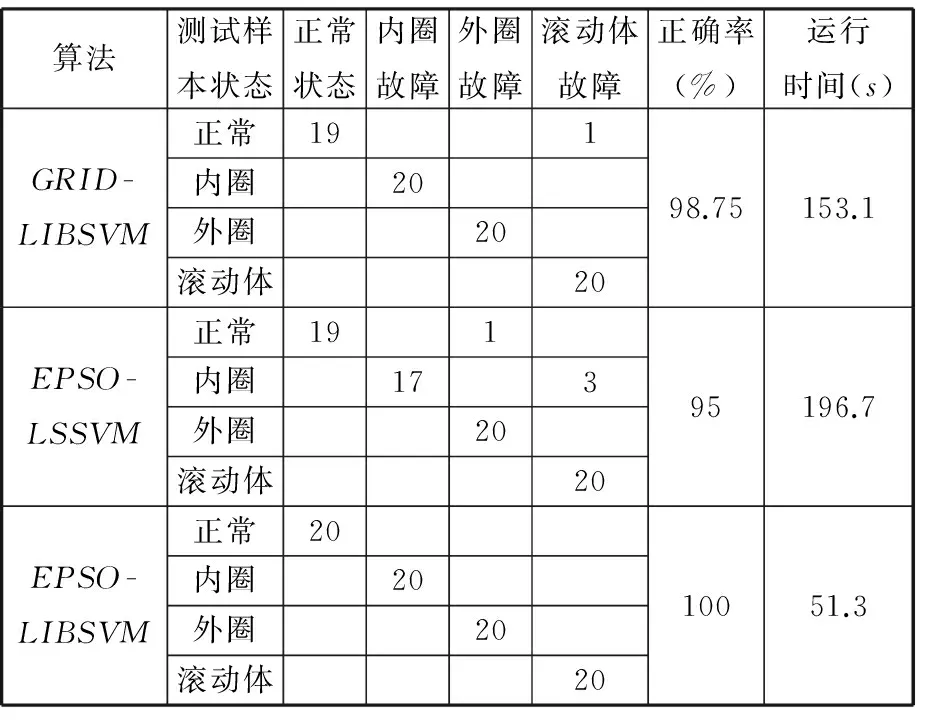
表2 三种识别算法故障诊断结果对比

在电机负载即转速1797 r/min下，选取滚动轴承不同部位，损伤点直径为0.1778 mm的振动数据，从正常状态、内圈故障、外圈故障和滚动体故障中分别选取80组数据，采样频率为12 kHz，采样点数为1024。对正常状态、内圈故障、外圈故障、滚动体故障四种不同故障部位的信号通过MED处理后，再经过VMD分解为4个分量，分别求每个分量的模糊近似熵值以完成对每个分量特征值的量化。将求得的模糊近似熵值构成特征向量TVMD=(SfApEn1,SfApEn2，SfApEn3，SfApEn4)，随机选取40组作为训练样本如表3所示，剩下40组为测试样本。为对比分析，对同样信号通过MED处理后，采用LMD分解，根据特征筛选准则对PF分量进行筛选，选取前4个PF分量，计算其模糊近似熵值构成特征向量TLMD=(SfApEn1,SfApEn2，SfApEn3，SfApEn4)，如表4所示。其中类型1、2、3、4分别代表滚动轴承正常状态、内圈故障、外圈故障和滚动体故障。

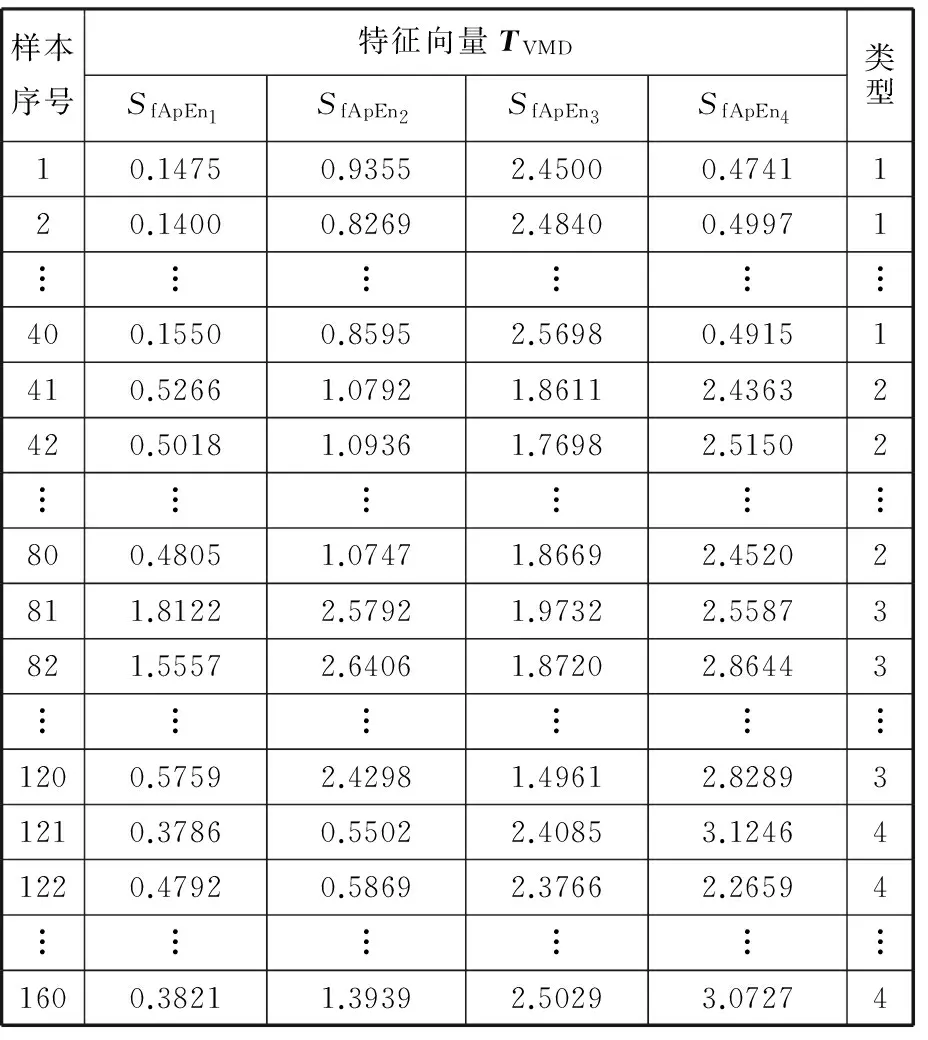
表3 由VMD各模态模糊近似熵构成的特征向量

将上述基于LMD和VMD方法进行特征提取所求得的特征向量，分别输入EPSO-LIBSVM中进行训练，并对测试样本进行识别，EPSO初始参数c1、c2为1.5、1.7，种群大小为20，迭代次数为200。基于LMD方法特征提取和基于VMD方法特征提取的识别结果分别如图13和图14所示，结果对比如表5所示。

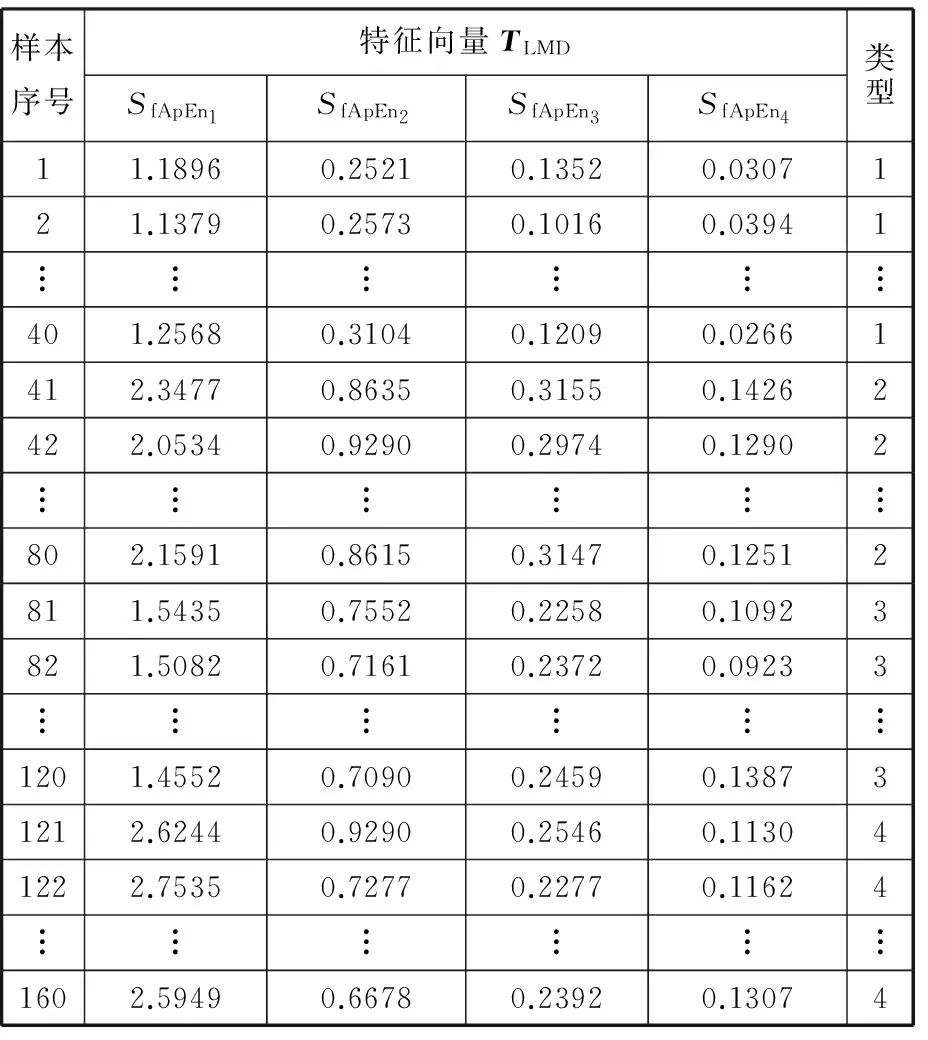
表4 由LMD各模态模糊近似熵构成的特征向量

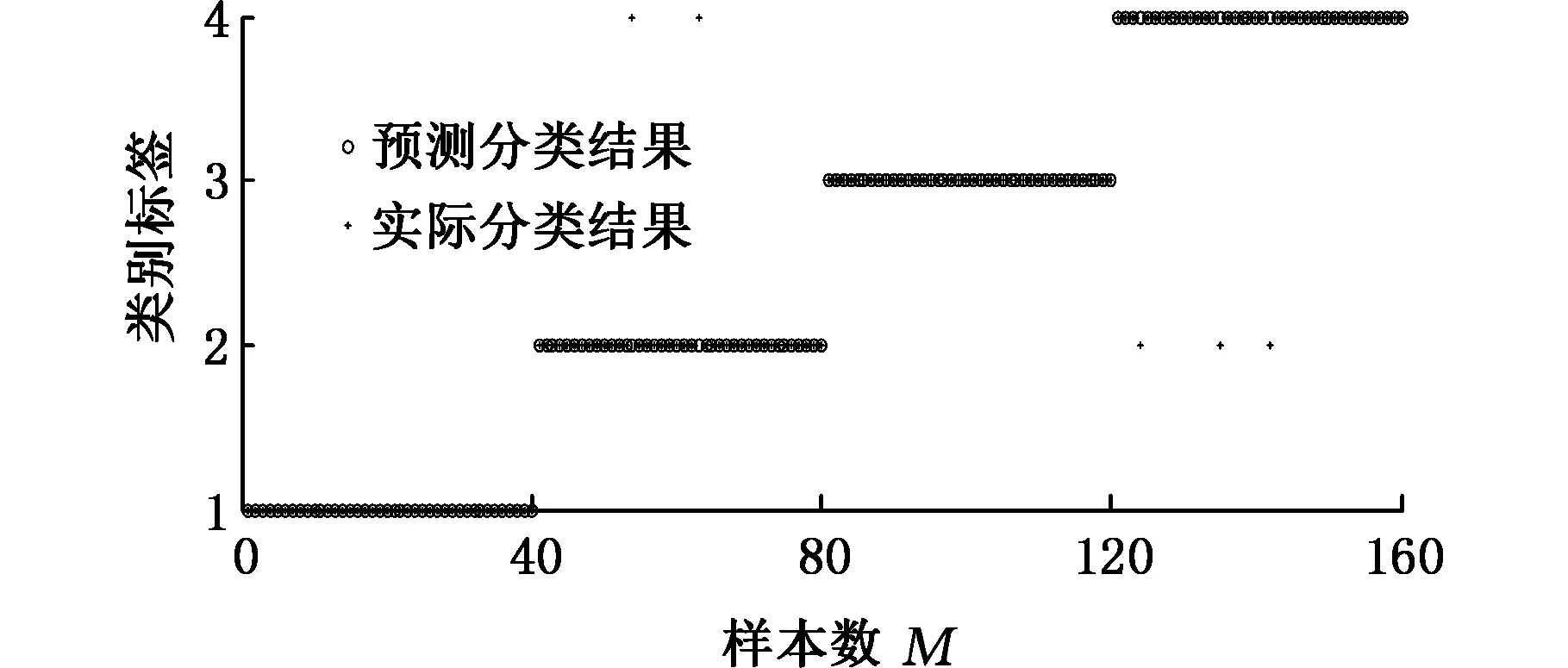
图13 基于LMD方法识别结果Fig.13 Recognition results based on LMD

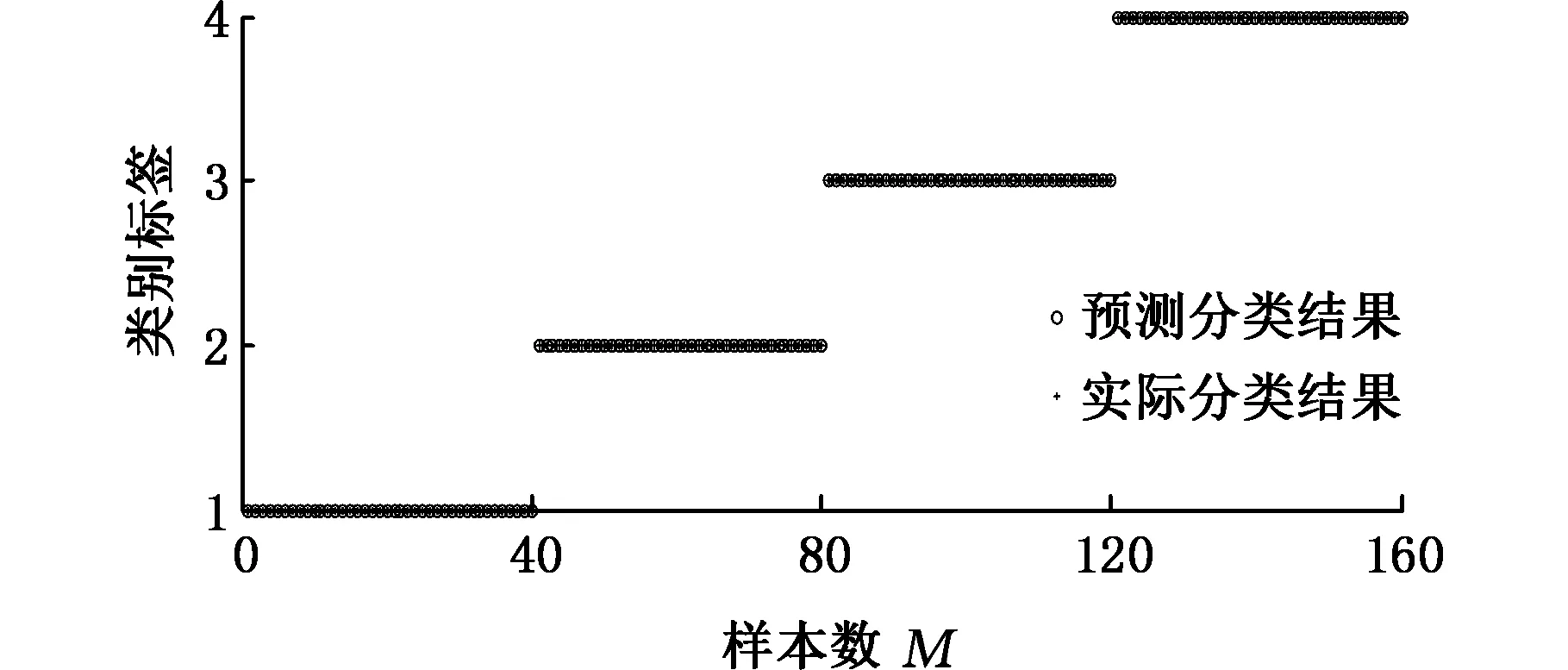
图14 基于VMD方法识别结果Fig.14 Recognition results based on VMD

通过表5可以看到，基于VMD方法可以正确识别出轻微损伤下滚动轴承不同故障部位，这有助于更好地发现滚动轴承早期故障，而基于LMD方法在内圈故障和滚动体故障之间出现了错分，从表4中可以看出，内圈故障所构成的特征向量与滚动体故障所构成的特征向量相似度较高，这即为内圈故障和滚动体故障之间出现错分的原因，有可能是因为LMD分解中存在模态混叠现象，这样会导致出现一些虚假成分，从而影响构建的特征向量。此结果表明，VMD方法相较于LMD方法可以更有效地提取出各频带的信息，从而更精确地提取出滚动轴承故障特征，并能够更准确地完成不同故障位置的识别。

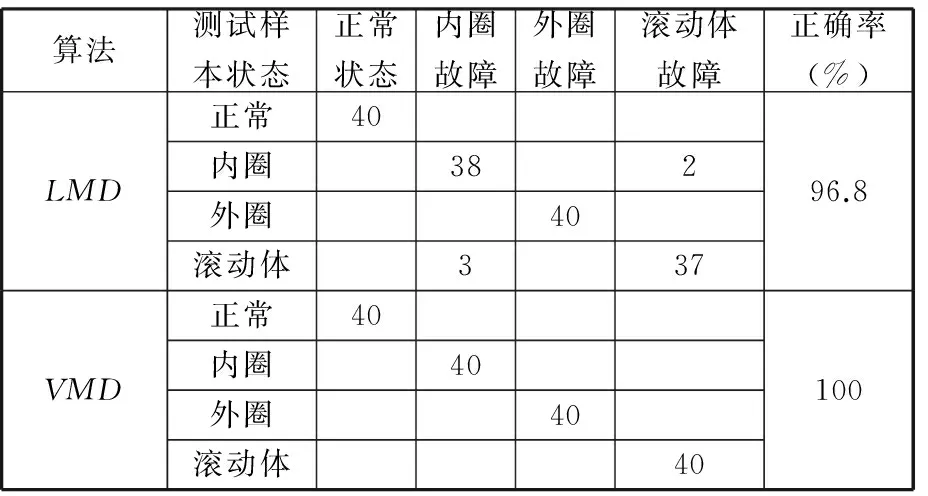
表5 不同特征提取方法结果对比

3.3 不同损伤程度故障诊断

采用驱动端下滚动轴承不同损伤程度的内圈故障信号进行分析，电机转速为1797 r/min，采样频率为12 kHz，将损伤程度分为轻微、中度和重度三种损伤程度，其损伤点直径分别为0.1778、0.3556、0.5334 mm，损伤点深度为0.2695 mm。

取电机转速1797 r/min下，正常状态、轻微损伤、中度损伤和重度损伤每种类型30组数据，数据长度为1024。在VMD分解后得到4个分量，由式(23)求每个分量的模糊近似熵值以完成对每个分量特征值量化。将求得的模糊近似熵值构成特征向量T=(SfApEn1,SfApEn2，SfApEn3，SfApEn4)。每种状态随机取20组为训练样本，剩下10组为测试样本。将80组训练样本的特征向量绘制成三维图，如图15所示，其中1、2、3、4分别代表不同分量的模糊近似熵值。通过三维图可以清晰地看到，滚动轴承不同损伤程度其特征向量之间具有明显差别，这验证了本文特征提取方法的有效性，也是之后对滚动轴承不同损伤程度识别正确率的保证。

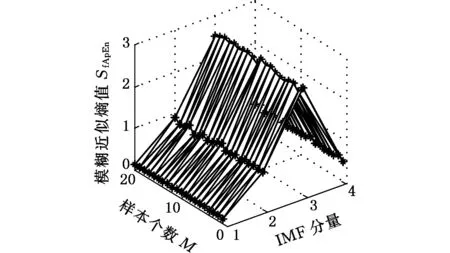
(a)正常状态特征向量

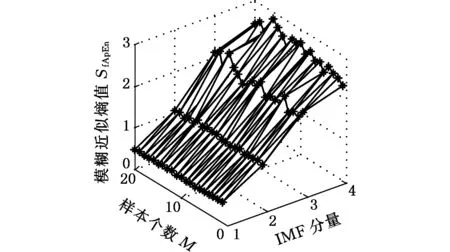
(b)轻微损伤特征向量

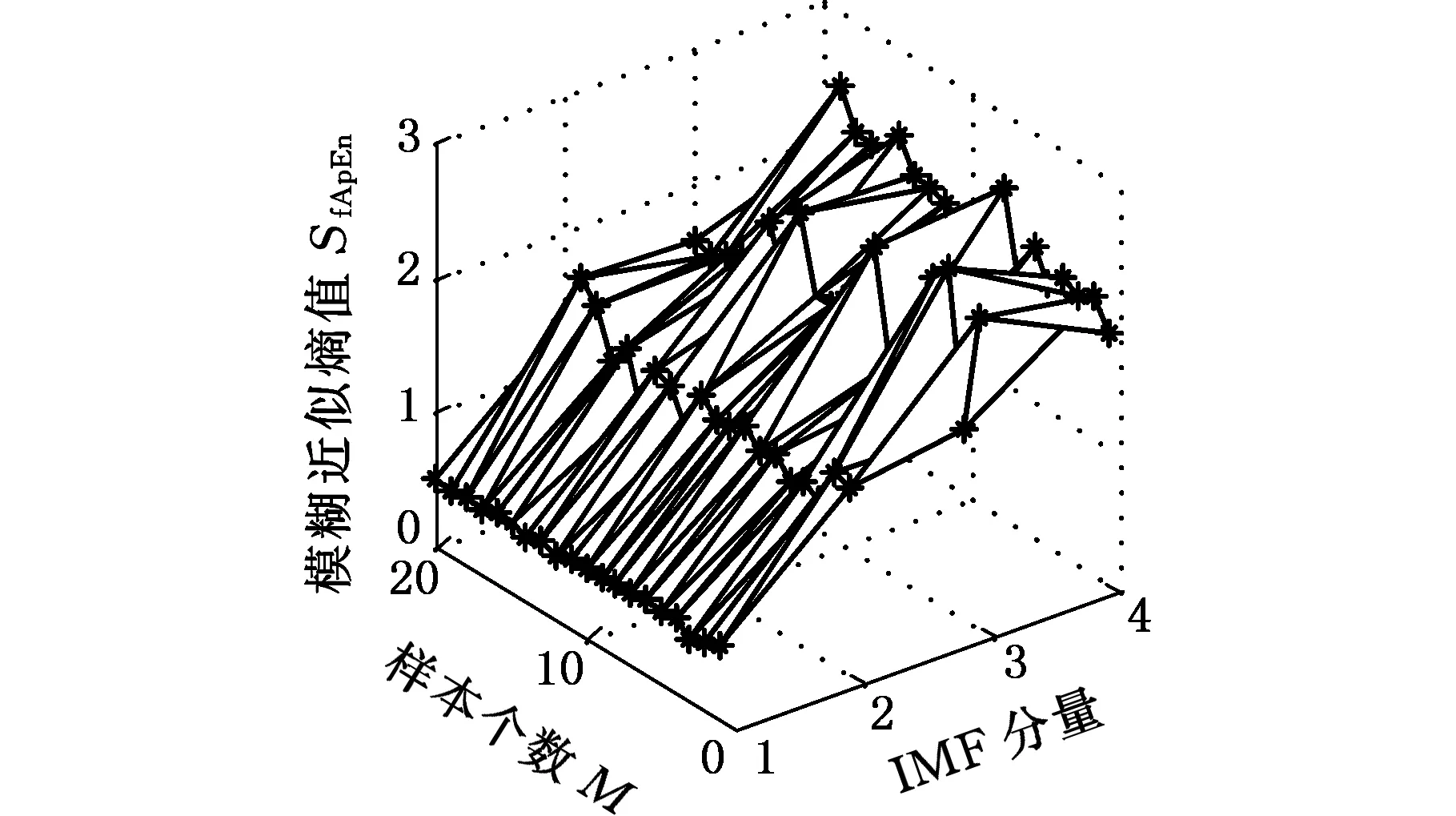
(c)中度损伤特征向量

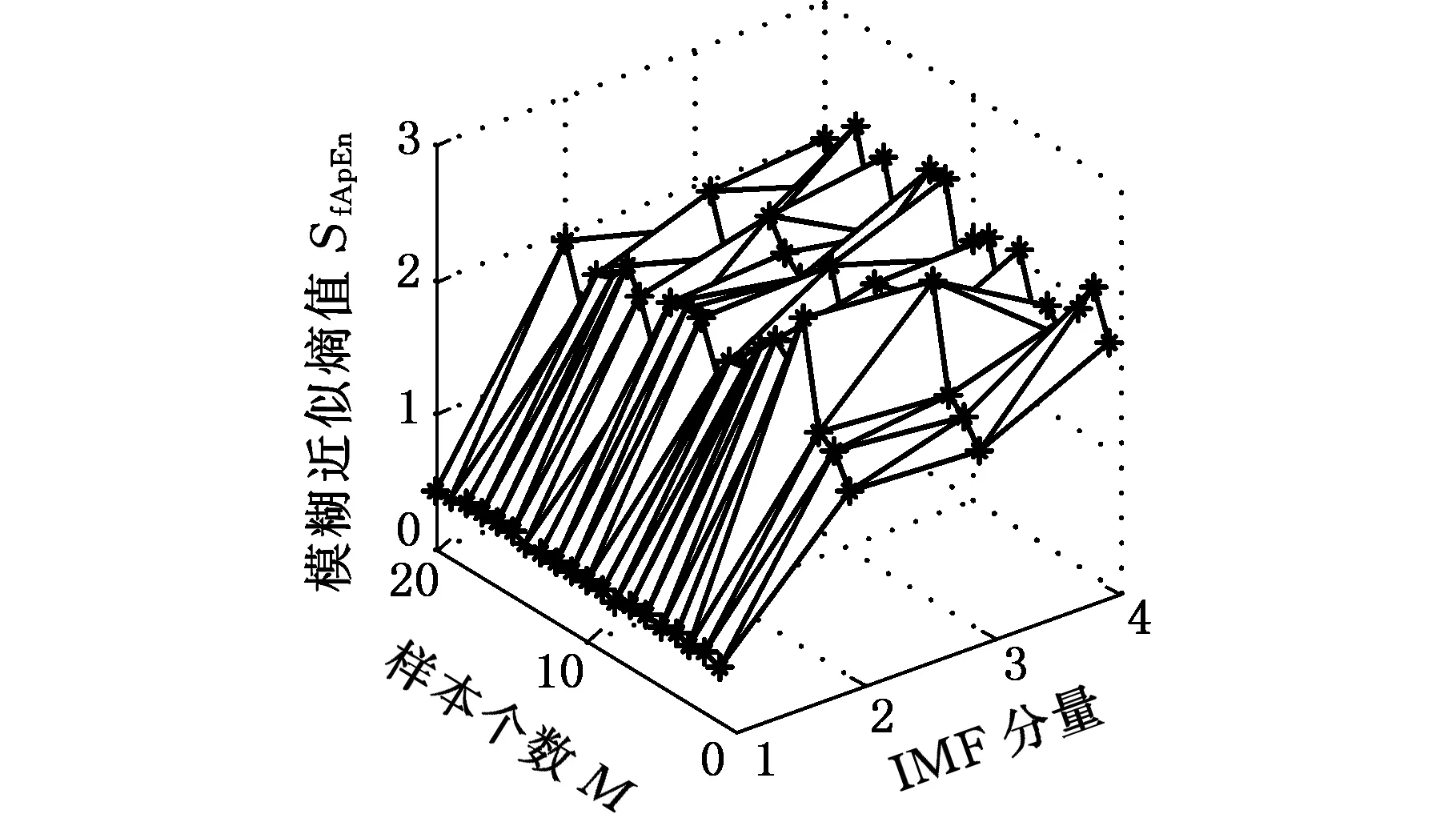
(d)重度损伤特征向量图15 不同损伤程度特征向量三维视图Fig.15 The 3D view of feature vectors in different damage degrees

将已知故障样本输入基于EPSO优化的LIBSVM中进行训练(图16)，EPSO初始参数c1、c2为1.5、1.7，种群大小为20，迭代次数为200次，得到最优LIBSVM参数C=19.53、σ=0.92。将待识别故障样本输入支持向量机模型进行识别，识别结果如图17和表6所示。

从图17和表6中可以看出，本文方法对40组待识别不同损伤程度样本均做出了正确的判断，从而可以验证，本文方法可以准确识别出滚动轴承不同损伤程度。

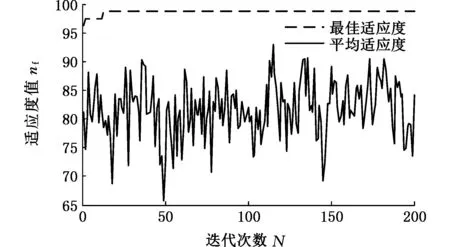
图16 EPSO优化LIBSVM适应度图Fig.16 Fitness diagram of LIBSVM optimized by EPSO

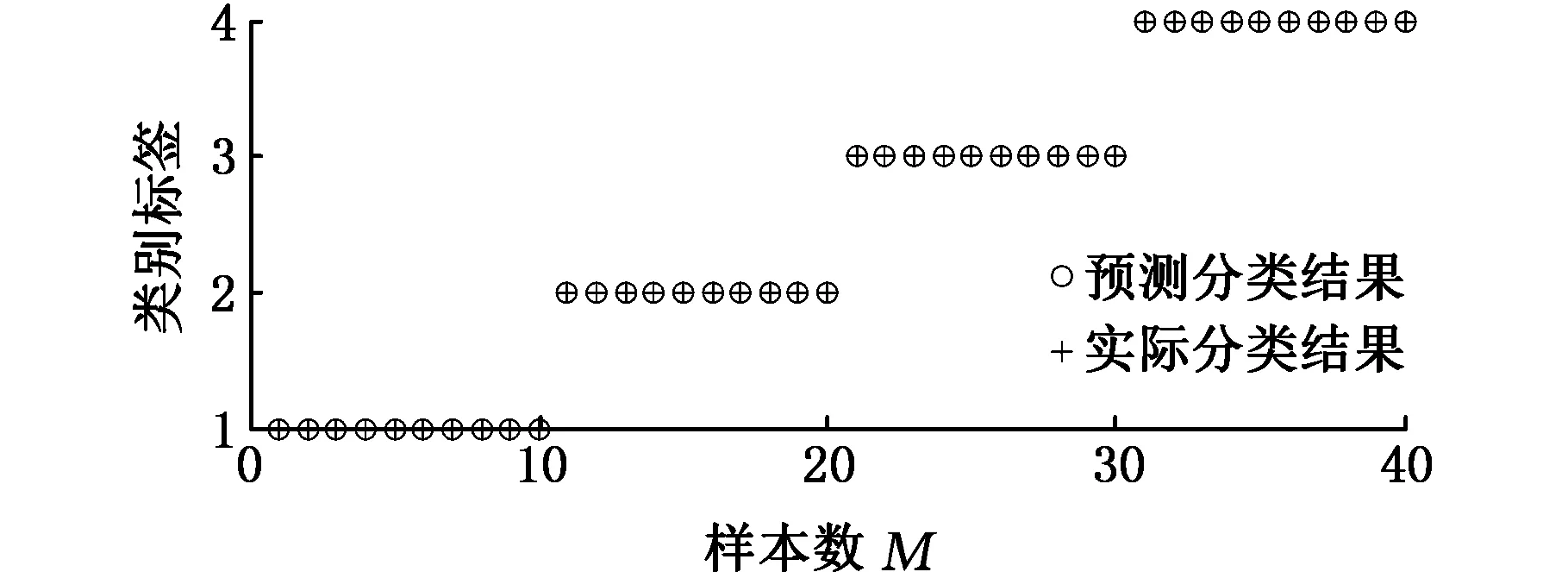
图17 滚动轴承不同损伤程度识别结果Fig.17 Recognition results of rolling bearing in different damage degrees

4 结论

(1) 针对滚动轴承振动信号非线性、非平稳特性以及故障特征信息易被噪声淹没的问题，提出最小熵解卷积和变分模态分解结合并以模糊近似熵构建特征向量的特征提取方法，通过最小熵解卷积方法对故障信号进行预处理，之后采用变分模态分解方法对其分解，最后使用模糊近似熵构建特征向量，该方法不但可有效降低噪声干扰，增强故障特征信息，避免传统信号分解导致的端点效应和模态混叠现象，而且使不同故障类型特征向量之间具有较大的区分度。实验结果表明，该方法可以有效地提取到故障特征信息。

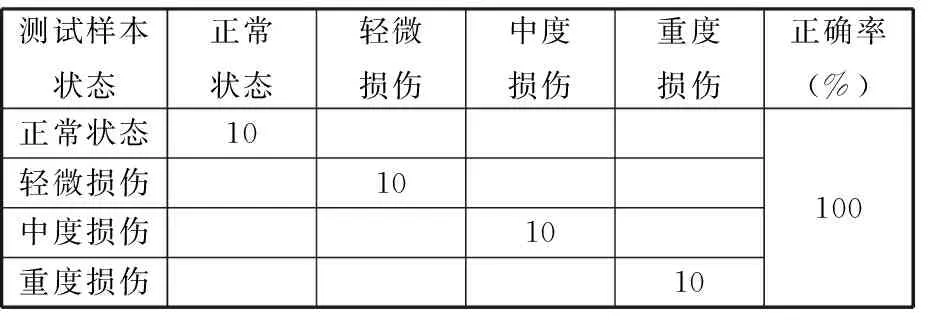
表6 不同损伤程度的识别

(2)针对支持向量机传统网格参数寻优方法效率低、难以搜索到最优参数的问题，提出基于扩展粒子群算法优化支持向量机的故障识别方法，利用扩展粒子群算法对支持向量机惩罚因子和核函数参数进行寻优搜索，实验结果表明，相对于基于网格参数寻优方法的支持向量机，基于扩展粒子群优化的支持向量机方法不但能以较短时间高效搜索出最优参数，而且该方法也具有更好的识别效果和识别准确率。

[1] 罗颂荣,程军圣,杨宇.基于本征时间尺度分解和变量预测模型模式识别的机械故障诊断[J].振动与冲击,2013,32(13):43-48.

LUO Songrong. CHENG Junsheng, YANG Yu. Machine Fault Diagnosis Method Using ITD and Variable Predictive Model-based Class Discrimination[J]. Journal of Vibration and Shock, 2013, 32(13): 43-48.

[2] 郑近德,潘海洋,戚晓利,等.复合层次模糊熵及其在滚动轴承故障诊断中的应用[J].中国机械工程,2016,27(15):2048-2055.

ZHENG Jinde, PAN Haiyang, QI Xiaoli, et al. Composite Hierarchical Fuzzy Entropy and Its Applications to Rolling Bearing Fault Diagnosis[J]. China Mechanical Engineering, 2016, 27(15): 2048-2055.

[3] BANERJEE S, MITRA M. Application of Cross Wavelet Transform for ECG Pattern Analysis and Classification[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(2): 326-333.

[4] 丁建明,王晗,林建辉,等.基于EMD-Hankel-SVD的高速列车万向轴动不平衡检测[J].振动与冲击,2015,34(9):164-170.

DING Jianming, WANG Han, LIN Jianhui, et al. Detection of Dynamic Imbalance Due to Cardan Shaft in High-speed Train Based on EMD-Hankel-SVD Method[J]. Journal of Vibration and Shock, 2015, 34(9): 164-170.

[5] 卞家磊,朱春梅,蒋章雷,等.LMD-ICA联合降噪方法在滚动轴承故障诊断中的应用[J].中国机械工程,2016,27(7):904-910.

BIAN Jialei, ZHU Chunmei, JIANG Zhanglei, et al. Application of LMD-ICA to Fault Diagnosis of Rolling Bearings[J]. China Mechanical Engineering, 2016, 27(7): 904-910.

[6] DRAGOMIRETSKIY K, ZOSSO D. Variational Mode Decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.

[7] 王建国,吴林峰,秦绪华.基于自相关分析和LMD的滚动轴承振动信号故障特征提取[J].中国机械工程,2014,25(2):186-191.

WANG Jianguo, WU Linfeng, QIN Xuhua. Rolling Bearing Vibration Signal Fault Feature Extraction Based on Autocorrelation Analysis and LMD[J]. China Mechanical Engineering, 2014, 25(2): 186-191.

[8] 臧怀刚,刘子豪,李玉奎.基于形态滤波和Laplace小波的轴承故障诊断[J].中国机械工程,2016,27(9):1198-1203.

ZANG Huaigang, LIU Zihao, LI Yukui. Fault Diagnosis of Bearings Based on Morphological Filter and Laplace Wavelet[J]. China Mechanical Engineering, 2016, 27(9): 1198-1203.

[9] KIM T, LEE K K. Estimation of Relative Recharge Sequence to Groundwater with Minimum Entropy Deconvolution[J]. Journal of Hydrology, 2005, 311: 8-19.

[10] HE D, WANG X, LI S, et al. Identification of Multiple Faults in Rotating Machinery Based on Minimum Entropy Deconvolution Combined with Spectral Kurtosis[J]. Mechanical Systems and Signal Processing, 2016, 81: 235-249.

[11] SAWALHI N, RANDALL R B, ENDO H. The Enhancement of Fault Detection and Diagnosis in Rolling Element Bearings Using Minimum Entropy Deconvolution Combined with Spectral Kurtosis[J]. Mechanical Systems and Signal Processing, 2007, 21(6): 2616-2633.

[12] 龚廷恺,袁晓辉,王细洋.最小熵反褶积的数学形态法在滚动轴承故障特征提取中的应用[J].中国机械工程,2016,27(18):2467-2471.

GONG Tingkai, YUAN Xiaohui, WANG Xiyang. Applications of Mathematical Morphology Method to Fault Feature Extraction of Rolling Bearings Based on Minimum Entropy Deconvolution[J]. China Mechanical Engineering, 2016, 27(18): 2467-2471.

[13] BARSZCZ T, SAWALHI N. Fault Detection Enhancement in Rolling Element Bearings Using the Minimum Entropy Deconvolution[J]. Archives of Acoustics, 2012, 37(2): 131-141.

[14] GUO H, WANG W. An Active Learning-based SVM Multi-class Classification Model[J]. Pattern Recognition, 2015, 48(5): 1577-1597.

[15] 万鹏, 王红军, 徐小力. 局部切空间排列和支持向量机的故障诊断模型[J]. 仪器仪表学报, 2012, 33(12): 2789-2795.

WAN Peng, WANG Hongjun, XU Xiaoli. Fault Diagnosis Model Based on Local Tangent Space Alignment and Support Vector Machine[J]. Chinese Journal of Scientific Instrument, 2012, 33(12): 2789-2795.

[16] 张淑清,胡永涛,姜安琦,等.基于双树复小波和自适应权重和时间因子的粒子群优化支持向量机的轴承故障诊断[J].中国机械工程,2017,28(3):327-333.

ZHANG Shuqing, HU Yongtao, JANG Anqi, et al. Bearing Fault Diagnosis Based on DTCWT and AWTFPSO-optimized SVM[J]. China Mechanical Engineering, 2017, 28(3): 327-333.

[17] 孟宗,李晶,龙海峰,等.基于压缩信息特征提取的滚动轴承故障诊断方法[J].中国机械工程,2017,28(7):806-812.

MENG Zong, LI Jing, LONG Haifeng, et al. Fault Diagnosis Method for Rolling Bearings Based on Compression Information Feature Extractions[J]. China Mechanical Engineering, 2017, 28(7): 806-812.

[18] 莫思敏,曾建潮,谢丽萍.扩展的微粒群算法[J].控制理论与应用,2012,29(6):811-816.

MO Simin, ZENG Jianchao, XIE Liping. Extended Particle-swarm Optimization Algorithm[J]. Control Theory and Applications, 2012, 29(6): 811-816.

[19] YAO Chengyu, WANG Bin, CHEN Dongning. Reliability Optimization of Multi-State Hydraulic System Based on T-S Fault Tree and Extended PSO Algorithm[C]//Proceeding of the 6th IFAC Symposium on Mechatronic Systems(IFAC MECH2013). Hangzhou, 2013: 463-468.

FaultDiagnosisMethodBasedonMED-VMDandOptimizedSVMforRollingBearings

YAO Chengyu1LAI Bowen1CHEN Dongning2,3SUN Fei2,3LYU Shijun2,3

1.Key Laboratory of Industrial Computer Control Engineering of Hebei Province,Yanshan University,Qinhuangdao,Hebei,066004 2.Hebei Provincial Key Laboratory of Heavy Machinery Fluid Power Transmission and Control,Yanshan University,Qinhuangdao，Hebei,066004 3.Key Laboratory of Advanced Forging & Stamping Technology and Science(Yanshan University), Ministry of Education of China,Qinhuangdao，Hebei,066004

A method of fault feature extraction was proposed based on MED, VMD and fuzzy approximate entropy, and the optimized SVM was used to identify faults. The MED method was used to reduce the noise interferences and to enhance the fault feature informations in the fault signals, and the signals after noise reduction by VMD were decomposed, then, the fuzzy approximation entropy was used to quantify the modal components of fault feature informations after VMD, and the feature vectors were constructed, Finally, the extended particle swarm optimization(EPSO) algorithm was used to optimize the penalty factors and the kernel function parameters of SVM to complete the fault recognition classification. The proposed method was applied to the experimental data of rolling bearings, and the effectiveness of the method was verified. Compared with the feature extraction method based on local mean decomposition(LMD), it is shown that the proposed method may extract the features of rolling bearing faults more accurately and may identify different faults more accurately. Compared with SVM based on grid search algorithm and the least square support vector machines(LSSVM) based on EPSO algorithm, the proposed method has better classification performance and better diagnosis performance.

fault diagnosis; variational mode decomposition(VMD); minimum entropy deconvolution(MED); fuzzy approximate entropy; support vector machine(SVM)

2017-06-06

国家自然科学基金资助项目(51675460，51405426)；河北省自然科学基金资助项目(E2016203306)；中国博士后科学基金资助项目(2017M621101)

TH165.3；TH133.33

10.3969/j.issn.1004-132X.2017.24.017

(编辑王艳丽)

姚成玉，男，1975年生。燕山大学电气工程学院教授、博士。主要研究方向为系统可靠性与故障诊断。获省部级科技二、三等奖共3项。出版著作3部，发表论文90余篇。E-mail: chyyao@ysu.edu.cn。来博文，男，1991年生。燕山大学电气工程学院硕士研究生。陈东宁，女，1978年生。燕山大学机械工程学院副教授、博士后研究人员。孙飞，男，1991年生。燕山大学机械工程学院硕士研究生。吕世君，男，1975年生。燕山大学机械工程学院讲师、博士研究生。