基于弧长参数的Akima刀位轨迹拟合算法研究

周 鹏 吴继春 周会成 杨世平 刘金刚 马秋成

1.湘潭大学复杂轨迹加工工艺及装备教育部工程中心，湘潭，4111052.华中科技大学国家数控系统工程技术研究中心,武汉，430074

基于弧长参数的Akima刀位轨迹拟合算法研究

周 鹏1吴继春1周会成2杨世平1刘金刚1马秋成1

1.湘潭大学复杂轨迹加工工艺及装备教育部工程中心，湘潭，4111052.华中科技大学国家数控系统工程技术研究中心,武汉，430074

在数控加工中，通常用小线段表达刀位轨迹，往往会导致刀位点庞大且轨迹不平滑。基于Akima曲线具有光顺连接且端点连接处保证G1以上连续等特点，将刀位点拟合成Akima样条曲线，提出了基于弧长参数的保凸Akima拟合刀位轨迹算法。该算法分为刀位点搜索和拟合两个阶段：首先利用拟合刀位轨迹的误差测试(双弦误差测试和弦切误差测试)约束，获得该段的首末刀位点；然后在该段内根据首末刀位点计算切线矢量，用弧长信息对刀位点参数化，生成一段Akima样条。利用UG软件生成了内含75个刀位点的鞋底模型，通过MATLAB编程和仿真实验，设置不同测试阈值，对比了弧长参数化Akima曲线与节点参数化Akima曲线、NURBS曲线之间的拟合效果，验证了算法的有效性。

小线段；Akima算法；弧长参数；双弦误差测试法；弦切误差测试法

0 引言

随着数控技术的日臻完善以及人们对加工产品要求的日趋多样化，以简单的直线插补和圆弧插补见长的传统数控插补技术,用于自由曲线或曲面加工已经不能达到理想的效果。自由曲线、曲面是一种复杂的几何形状，如飞机机翼、发动机的叶片、凸轮曲面轮廓以及复杂模具的型腔等，其解析表达式一般难以求得，且对于复杂轮廓，根据加工精度和加工余量等约束条件生成的刀位文件过大，能达到十几兆甚至几百兆。NURBS方法具有将刀位点拟合成高阶连续的效果且使刀位文件减小[1-5]，但是段与段之间只是C0连续，且实时计算量大。针对实际刀位点分布不均的特点，用NURBS曲线拟合可能出现曲线扭曲等现象，因此既要保证段内与段间有较好的连续性，也要降低拟合曲线的失真度，采用Akima算法拟合刀位点不失为一种好的选择。来燕菁等[6]比较了Akima插值曲线的累加弦长参数化法与修正弦长参数化法，并通过仿真得出后者生成的曲线更接近理想曲线的结论。ALEXANDRU[7]针对Akima曲线的端点提出了误差估计优化算法。袁维涛等[8]利用Akima插值算法在数控系统中以高级宏程序实现了凸轮的数控编程加工。由于Akima插值算法自身具有G1连续和较小的节点影响因子的优势，尤其是其中一个节点改变影响其周围6个节点的特征[9]，这对于约束数据量大的刀位点是十分有利的。TAO等[10]将双Akima样条曲线插值用于连接数控加工中的刀位点，比传统三维弦长法更为有效地减少数据点，从而获得更加光滑的加工/拟合表面。刘俊等[11]提出了对CAD模型的B样条曲线曲面密集控制点进行压缩编码的二阶预测编码算法。本文提出基于弧长参数的约束刀位点Akima拟合算法，在测试约束(双弦测试法和弦高测试法)的条件下，搜索不满足测试阈值的相邻刀位点并进行分段拟合，在不同阈值下对Akima曲线的相关误差进行分析，并在MATLAB实验中验证算法的有效性。

1 Akima算法的基本原理

Akima算法是Hiroshi Akima于1970年提出的一种曲线拟合算法，它是一种在已知数据点间建立一阶导数连续的三次多项式算法[12]。在每两个数据点间建立一条三次拟合曲线，整条曲线保证一阶导数连续，该算法也被称为五点拟合算法。

已知n个数据点pi(xi,yi)(i=0,1,…,n-1),在两相邻数据点pi(xi,yi)和pi+1(xi+1,yi+1)间确定一个三次多项式：

r(u)=Ai+Bi(u-ui)+Ci(u-ui)2+
Di(u-ui)3

(1)

u∈[ui-1,ui]

(2)

k=1,2,…,n-1

式中，uk为刀位点的节点参数;Ai、Bi、Ci、Di均为系数向量。

式(1)称为“节点参数化”的Akima曲线多项式，该Akima曲线称作“节点参数化Akima曲线”。

为了得到式(1)的三次多项式，需要确定其中的系数向量Ai、Bi、Ci和Di，计算表达式为

(3)

k=1,2,…，n-1i=1,2,…,n-1

式中，mk为pi(xi,yi)和pi+1(xi+1,yi+1)两数据点间线段的斜率向量；s(ui)为pi(xi,yi)和pi+1(xi+1,yi+1)两数据点间线段的切线向量。

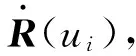
2 基于弧长参数的约束刀位点Akima拟合算法

2.1 基于测试约束的刀位点分段

在数控加工中，不同的曲线或曲面轮廓对应不同的刀位点分布，根据加工件轮廓的复杂程度，生成的刀位点大多数是疏密不一的，平坦的局部轮廓曲线的刀位点比较分散，有曲率的轮廓处的刀位点则相对密集，而且曲率越大，刀位点密集度越大。

针对刀位点的疏密程度，考虑利用Akima曲线误差测试约束对刀位点进行分段的预处理。Akima曲线误差测试包括双弦误差测试和弦切误差测试。如图1所示，给定任意依次连接的3个刀位点Pi-1、Pi和Pi+1，ai-1和ai是相邻刀位点之间的连线长度，R是通过Pi-1、Pi和Pi+1的圆半径，δ1和δ2是双弦误差。如果弦误差δ1和δ2同时都小于设定的最大轮廓误差δmax,那么相邻两条小线段Pi-1Pi和PiPi+1就可以看成一条符合Akima曲线拟合条件的连续小线段。

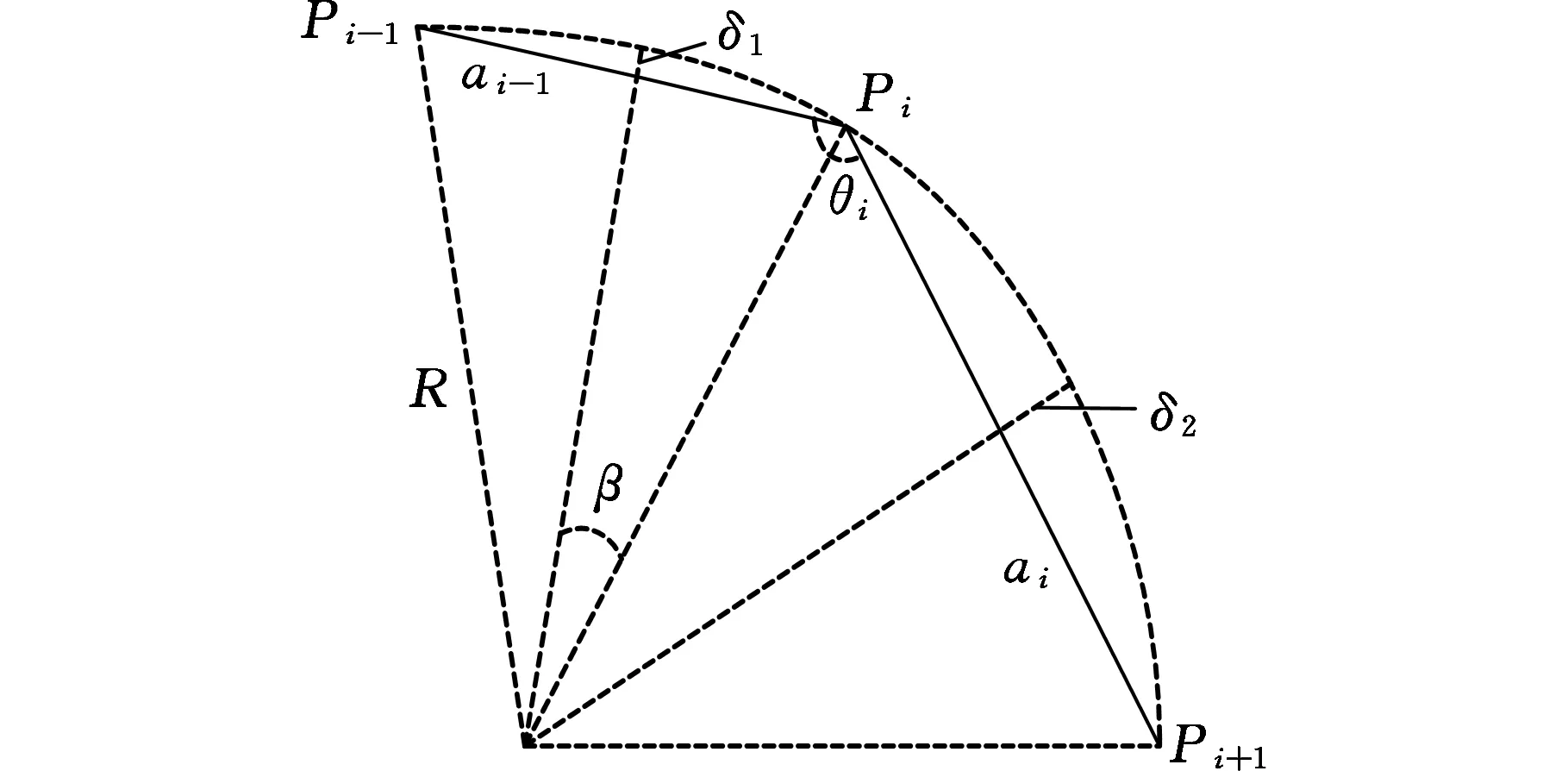
图1 双弦误差Fig.1 The bi-chord error

在满足上述双弦误差条件的前提下，对于任意两个刀位点Pi和Pi+1，必须符合弦切误差标准，如图2所示，点M是分别过点Pi和Pi+1的两条切线的交点，d是交点M到直线PiPi+1的距离，PiM和Pi+1M分别是点Pi和Pi+1处的弦切值。

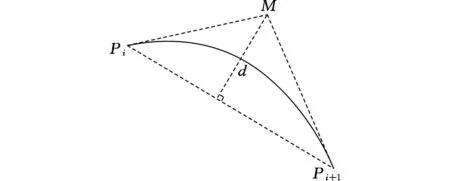
图2 弦切误差Fig.2 The tangent-chord error

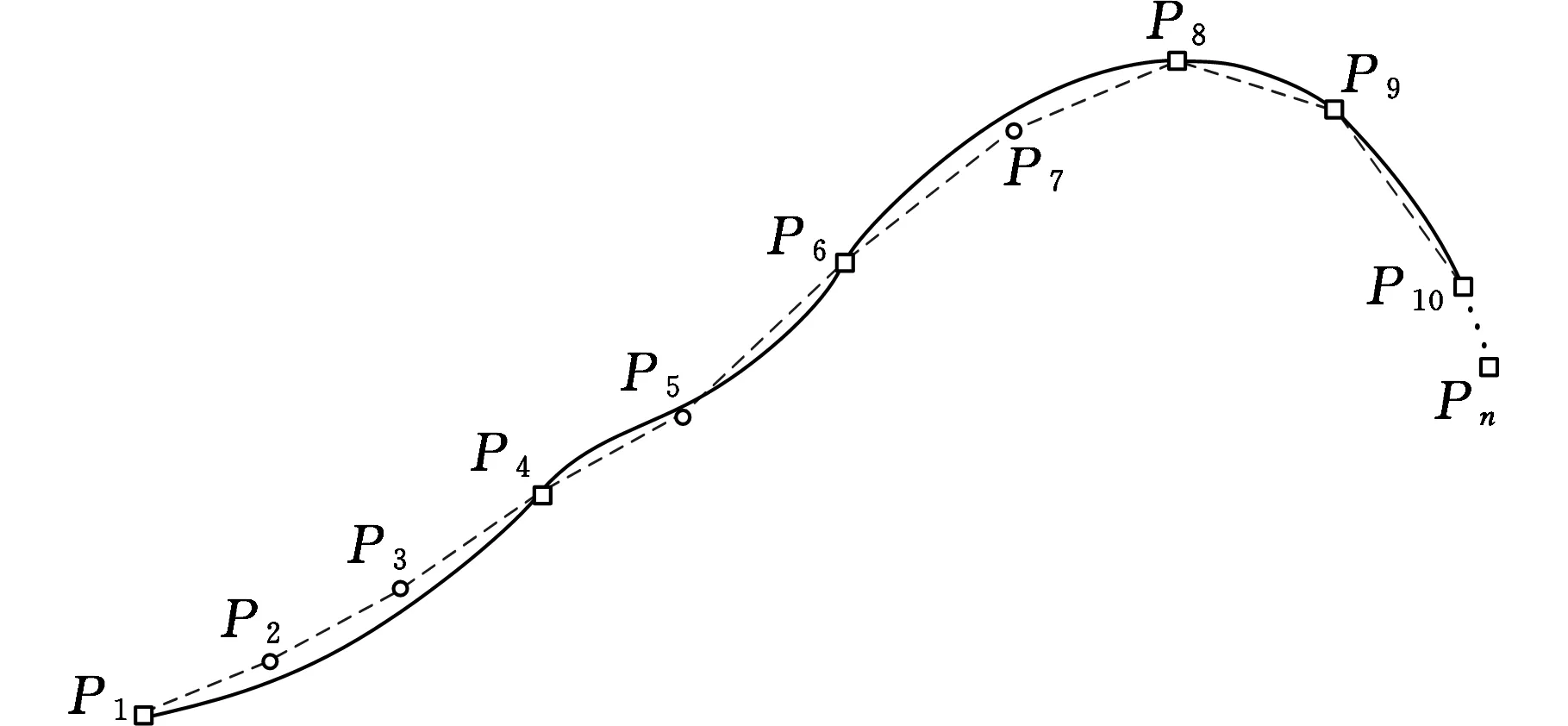
图3 刀位点约束分段拟合示意图Fig.3 The segmented fitting with CL points

2.2 刀位点的弧长参数化

针对刀位点的Akima分段拟合，在进行刀位点搜索时，随着搜索持续和中止的交替进行，拟合分段数不断发生变化，而节点参数ui与刀位点分段有关，根据刀位点的累计弦长计算每个刀位点的节点参数，因此可将刀位点弧长参数化，实现Akima刀位轨迹拟合方法。

计算斜率向量(mix,miy]，其表达式为

(4)

i=1,2,…,n-1

其中，li表示相邻刀位点的弧长，考虑刀位点距离不均和计算方便，用双弦误差测试方法中的圆弧[9]近似代替弧长：

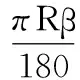
(5)

式中，R为弧长li所在的半径；β为li对应圆心角。

R与β的计算如下：

(6)

式中，θi为相邻弦长之间的夹角。

于是,弧长参数化Akima曲线为

ri(l)=Ai+Bi(l-li)+Ci(l-li)2+
Di(l-li)3

(7)

l∈[0,li]

i=1,2,…，n-1

由于计算需要，在首末刀位点处补充4个辅助斜率向量，计算如下：

(8)

s(li)=

(9)

i=1,2,…,n-1

依次由式(6)、式(7)、式(4)、式(8)和式(9)联立得出式(5)的系数向量Ai、Bi、Ci和Di，计算表达式为

(10)

i=1,2,…,n-1

在拟合中，前一段的末点已计算的切线向量保留为下一段起点切线向量，以保证拟合曲线的G1连续性，下一段末点切线向量，根据弧长参数化，依此递推方式计算。

如图4所示，点Pi,Pi+1,…,Pi+5分别是2.1节中搜索中止的部分刀位点，ai,ai+1,…，ai+4分别是搜索中止的相邻刀位点之间的距离，li,li+1,…,li+4分别是3个相邻刀位点之间的圆弧长度，近似为相邻刀位点的曲线弧长。按图中箭头的方向，保留Pi点的切线向量s(li)，在未知全部刀位点的前提下，搜索下一个刀位点Pi+1，通过弧长参数化，计算Pi+1点的切线向量s(li+1)，然后计算Pi与Pi+1段的Akima曲线r(l)(0≤l≤li)。同样保留该点的切线向量s(li+1)，继续向下搜索如图中的Pi+2、Pi+3、Pi+4、Pi+5时，在相邻刀位点之间依次利用弧长参数进行Akima曲线的递推式拟合，直至结束。

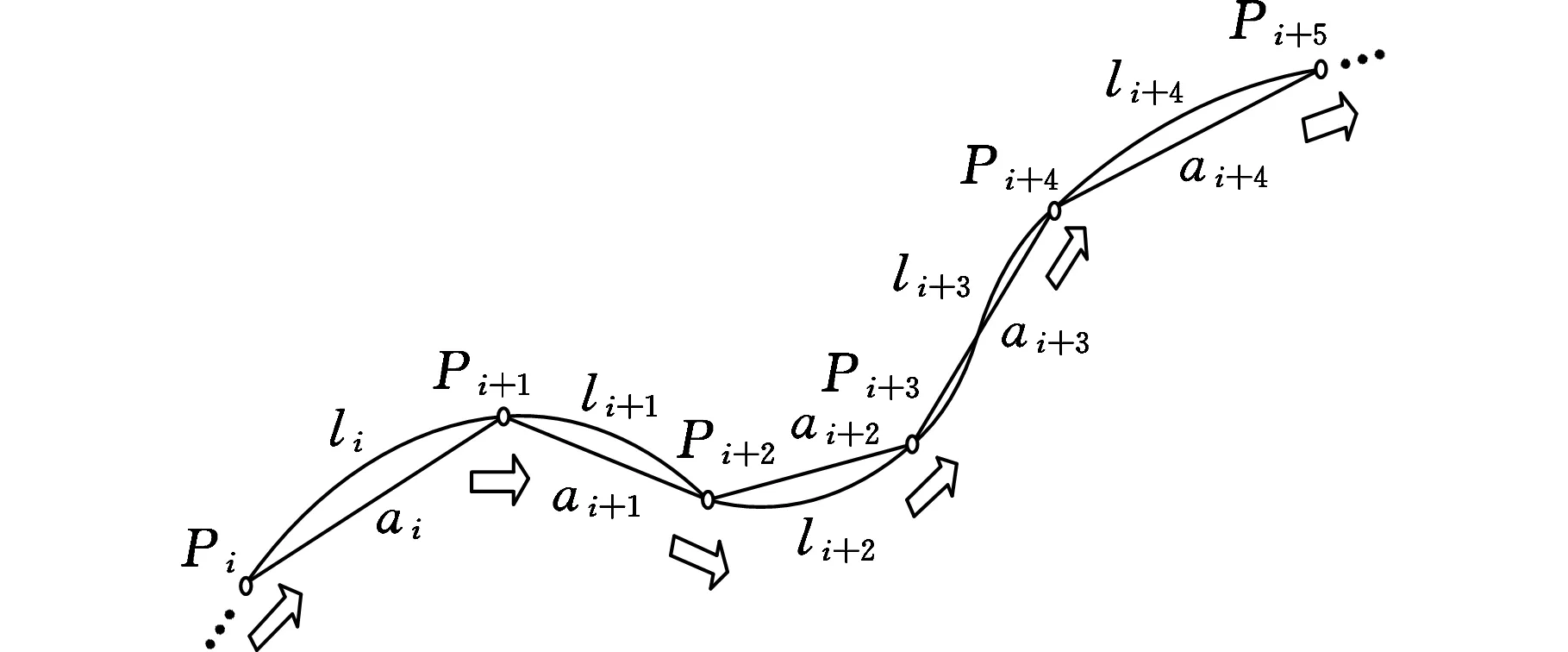
图4 刀位点弧长参数化递推示意图Fig.4 The recursive schematic of arc length parameterization

2.3 刀位点的约束算法流程

利用UG10.0软件, 以鼠标模型为加工实例，在选择好刀具、加工余量、加工方法等参数后，生成的刀位点云图见图5，图6是它的局部放大图。

图5 鼠标刀位点云图Fig.5 The Cl points with mouse map

图6 鼠标局部刀位点放大图Fig.6 Local CL points enlargement with mouse

采用基于弧长参数的Akima刀位轨迹拟合方法进行拟合，如图7所示。首先依据测试约束依次搜索要拟合段的终点刀位点 ，然后计算刀位点切线向量等几何信息，拟合Akima曲线。将搜索到的刀位点作为下一段Akima曲线的起点，继续搜索不满足阈值的刀位点，并作为下一段终点，且拟合该段Akima曲线。

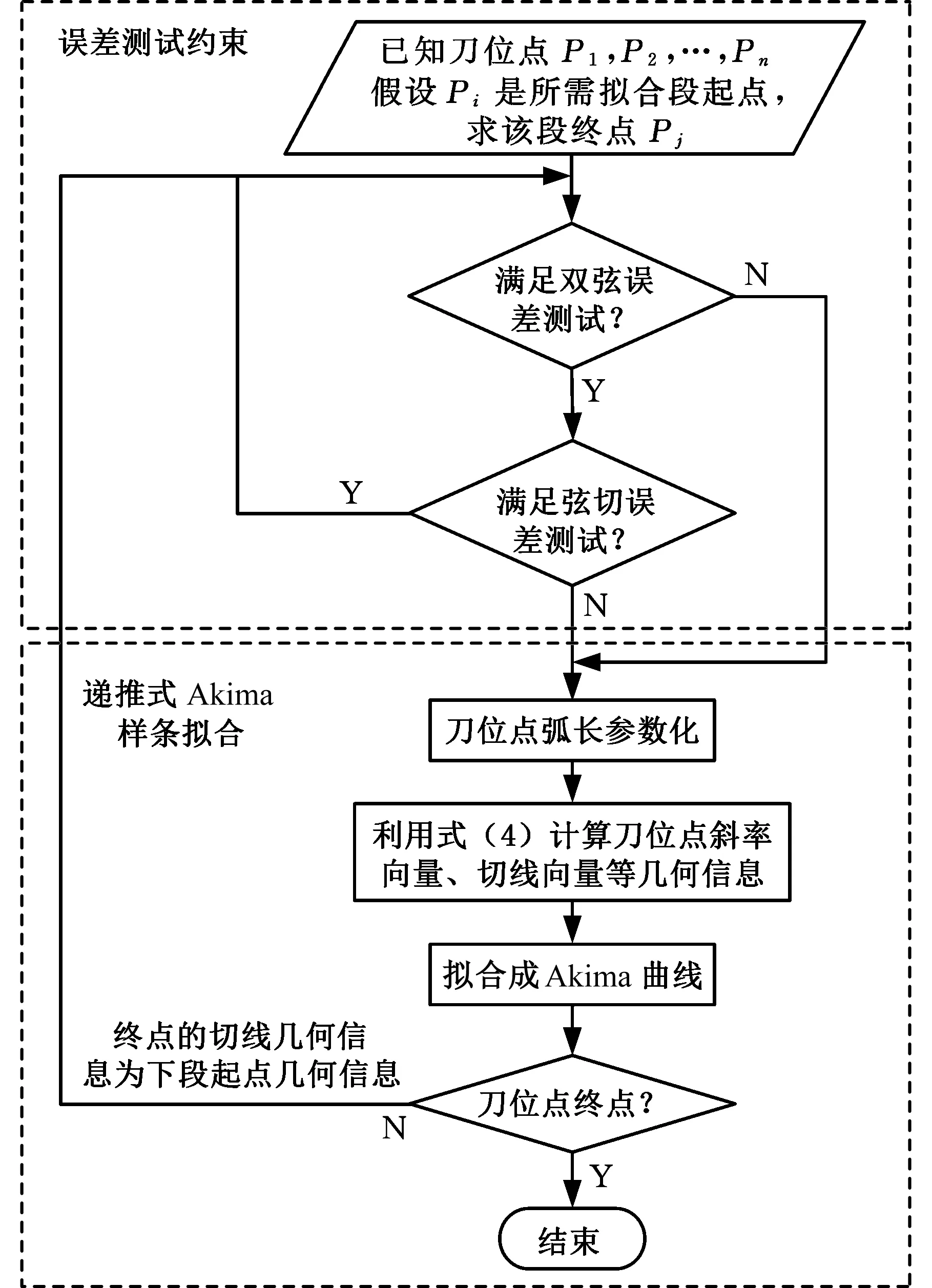
图7 弧长参数化的Akima拟合流程图Fig.7 Akima fitting flow chart with arc length parameterization

3 实例分析

为了验证本文提出的弧长参数化Akima曲线拟合方法，利用UG建立鞋底模型，生成75个刀位点NC文件。具体验证步骤是通过文献[9]中的节点参数化Akima曲线与本文方法进行同种曲线的“内部对比”，再与NURBS曲线进行曲线之间的“外部比较”，具体对比情况如图8与表1所示。

(a)Akima曲线与NURBS曲线对比图

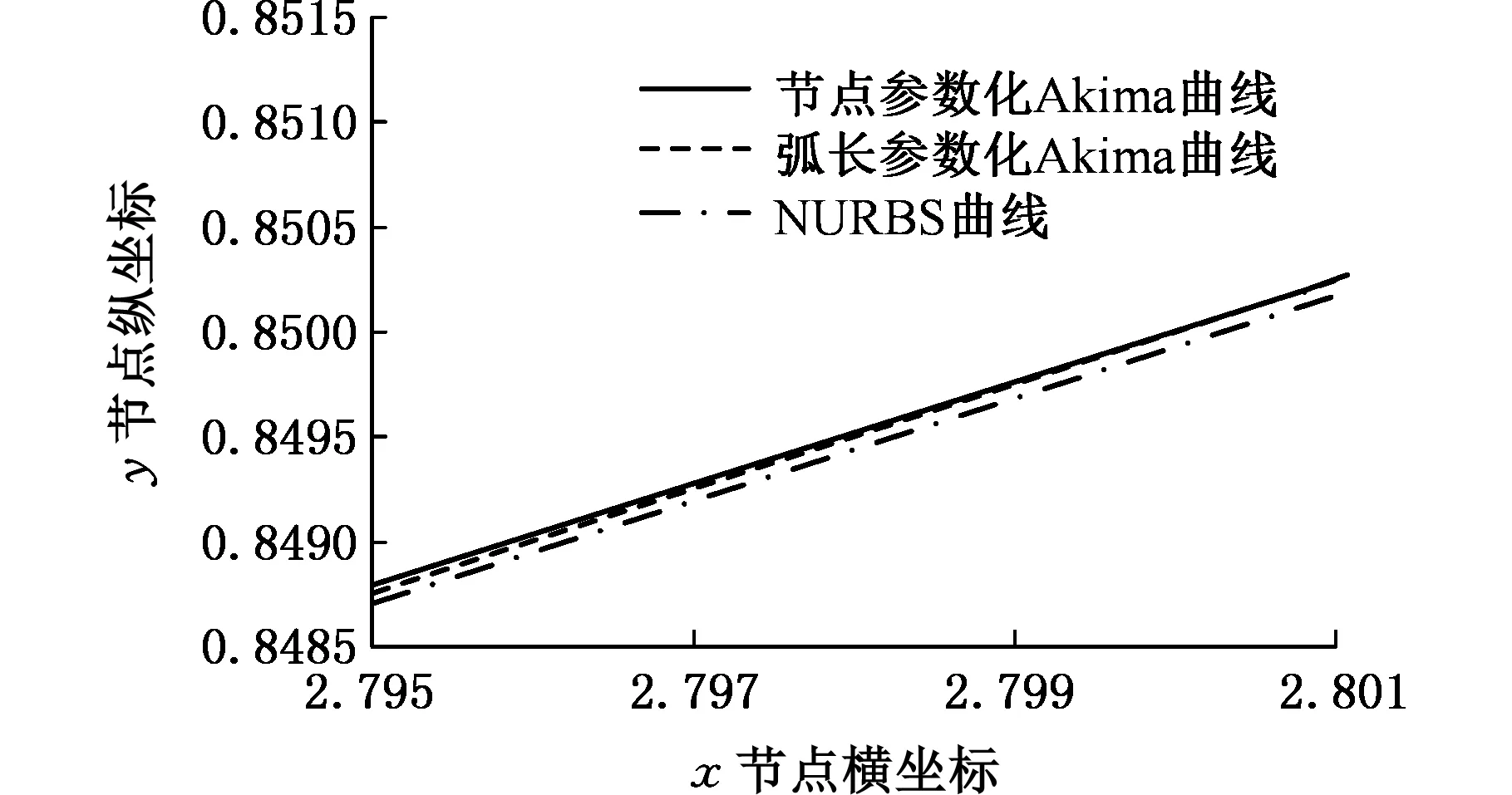
(b)1处的局部放大图

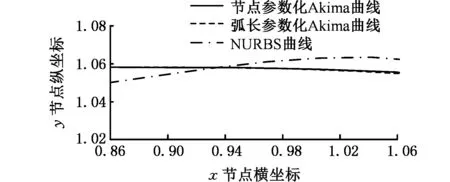
(c)2处局部放大图图8 三种曲线拟合方法对比Fig.8 Comparison of three curve fitting methods

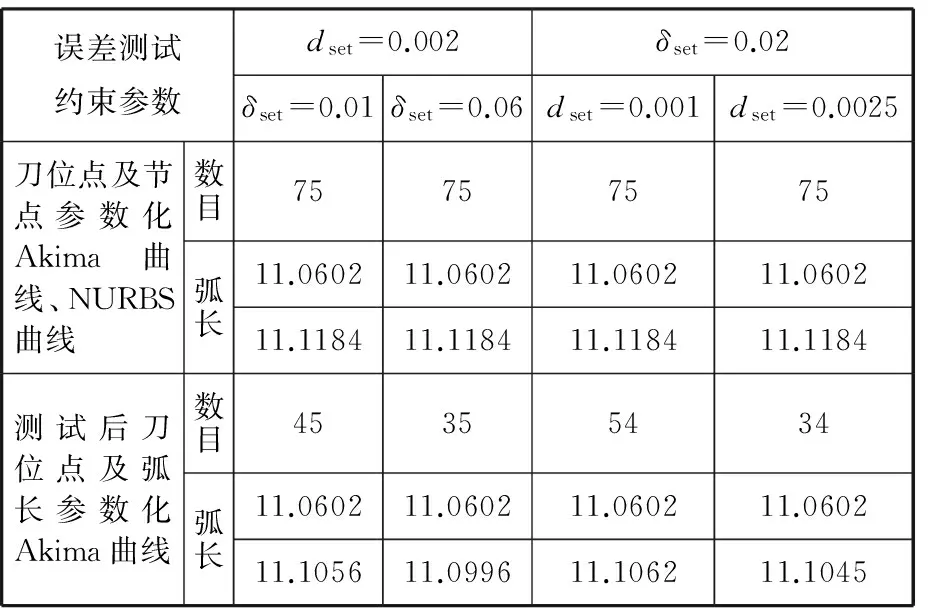
误差测试约束参数dset=0.002δset=0.02δset=0.01δset=0.06dset=0.001dset=0.0025刀位点及节点参数化Akima曲线、NURBS曲线数目75757575弧长11.060211.060211.060211.060211.118411.118411.118411.1184测试后刀位点及弧长参数化Akima曲线数目45355434弧长11.060211.060211.060211.060211.105611.099611.106211.1045

图8a是三种曲线拟合方法对比图，实线表示节点参数化曲线，虚线表示弧长参数化Akima曲线，点画线表示NURBS曲线。通过误差测试约束的弧长参数化Akima曲线与节点参数化Akima曲线、NURBS曲线从整体上看吻合程度较好，如图8b所示。图8c中两种Akima拟合方法逼近效果较好，而与NURBS 拟合曲线吻合效果不好，究其原因,NURBS没有通过刀位点,与Akima曲线有较大偏差，无论NURBS是逼近还是插值，所拟合曲线均是全局拟合且由控制点个数决定，同时与刀位点均匀分布紧密相关，当刀位点分布不均匀时，可能导致NURBS 曲线有扭曲现象。而弧长参数化Akima曲线是递推进行、局部拟合的，且具有弧长信息，为后续插补提供方便。

综上所述，在Akima曲线的“内部对比”方面，经误差测试约束的刀位点数与原始刀位点相比，数量有了很大减少，表明后续的拟合Akima曲线段数会有明显减少。设置不同参数，拟合Akima曲线的弧长与原始刀位点的弧长接近，表明曲线能够重构出原始的几何形状，且能保证曲线的凸凹性。设置不同误差测试约束参数，得到不同的测试后保留的刀位点；在曲线之间的“外部对比”方面，尽管NURBS曲线与Akima曲线的整体拟合效果比较接近，但在局部效果上，由于NURBS的曲线全局拟合性质，呈现出与Akima曲线有所偏差的拟合状态，且从拟合曲线弧长看，以节点参数化Akima曲线弧长为参考，NURBS曲线弧长比弧长参数化Akima曲线弧长略大(表1)。因此，基于鞋底模型的Akima与NURBS插值拟合刀位点约束算法的拟合效果相对较好的条件是：δset=0.02、dset=0.0025，约束后刀位点34个。

4 结论

为了将刀位点拟合成Akima样条曲线，本文提出了基于弧长参数的Akima刀位轨迹拟合算法。首先利用误差测试约束方法来选取拟合曲线的起止刀位点，然后对选取的刀位点进行弧长参数化，实现递推式拟合过程，即实现 “加入刀位点—对其进行弧长参数化—拟合Akima曲线”这种递推式拟合模式，且上一段终点刀位点切线向量等几何信息也是下一段起点的几何信息，不需要重复计算从而提高计算效率。利用UG生成的鞋底模型，通过误差测试约束刀位点，对比了弧长参数化Akima曲线与节点参数化Akima曲线、NURBS曲线之间的拟合，验证了提出方法的有效性。

[1] 周凯，谭仲毅.STEP-NC数控系统的NURBS曲面插补方法[J].制造技术与机床，2006(12):67-70.

ZHOU Kai, TAN Zhongyi. Interpolation Method of NURBS Curved Surface for STEP-NC Control System[J]. Manufacturing Technology & Machine Tool,2006(12):67-70.

[2] 杨群.基于UG的自由曲面设计及数控加工模拟[D].西安：西安理工大学，2002.

YANG Qun. Design of Free Surface Based on UG and Simulation of NC Machining[D]. Xi’an: Xi’an University of Technology, 2002.

[3] 温云龙.基于NURBS曲线的数控算法研究与设计[D].广州：华南理工大学，2011.

WEN Yunlong. Research and Design of NC Algorithm Based on NURBS Curve[D].Guangzhou: South China University of Technology, 2011.

[4] 王国勋，王宛山，王军，等.实时快速NURBS直接插补技术[J].中国机械工程，2013,24(5):617-622.

WANG Guoxun, WANG Wanshan, WANG Jun， et al. Real-time Fast NURBS Direct Interpolation Technology[J].China Mechanical Engineering, 2013,24(5):617-622.

[5] 杨萍，杨明泰，张阳阳.高速加工中NURBS曲线拟合及插补技术的研究[J].中国机械工程，2015,26(12):1630-1634.

YANG Pin, YANG Mingtai， ZHANG Yangyang. Research on NURBS Curve Fitting and Interpolation Technology in High Speed Machining[J]. China Mechanical Engineering, 2015,26(12):1630-1634.

[6] 来燕菁，张为民，齐党进，等.Akima曲线插补中的空间曲线多项式生成方法研究[J].制造技术与机床，2013(2):56-60.

LAI Yanqin, ZHANG Weimin, QI Dangjin， et al. Research on Generating Method of Space Curve Polynomial in Akima Curve Interpolation[J]. Manufacturing Technology & Machine Tool, 2013(2):56-60.

[7] ALEXANDRU M B. Optimizing at the End-points the Akima’s Interpolation Method of Smooth Curve Fitiing[J].Computer Aided Geometric Design,2014,31(5):245-257.

[8] 袁维涛，刘仁春.Akima插值法在凸轮加工中的应用[J].金属加工：冷加工，2015(5):71-73.

YUAN Weitao, LIU Renchun. Application of Akima Interpolation Method in Cam Machining[J]. Metalworking: Cold Working, 2015(5):71-73.

[9] WANG Yunsen, YANG Dongsheng, LIU Yinzhong. A Real-time Look-ahead Interpolation Algorithm Based on Akima Curve Fitting[J].International Journal of Machine Tools & Manufacture,2014,85(5):122-130.

[10] TAO Ye, WANG Yongqing, LIU Haibo, et al. On-line Three-dimensional Point Cloud Data Extraction Method for Scan-tracking Measurement of Irregular Surface Using Bi-Akima Spline[J].Measurement,2016,92:382-390.

[11] 刘俊，王启富，陈立平，等.B样条曲线曲面的二阶预测压缩算法[J].中国机械工程，2008，19(3):304-307.

LIU Jun, WANG Qifu, Chen Liping. Second-Order Predictive Compression Algorithm for B-Spline Curves and Surfaces[J]. China Mechanical Engineering, 2008，19(3):304-307.

[12] HIROSHI A. A New Method of Interpolation and Smooth Curve Fitting Based on Local Procedures[J].Journal of the Association for Computing Machinery,1970,17(4):589-602.

StudyonAkimaCurve-fittingAlgorithmwithTool-pathBasedonArc-lengthParameters

ZHOU Peng1WU Jichun1ZHOU Huicheng2YANG Shiping1LIU Jingang1MA Qiucheng1

1.The Engineering Center of Ministry of Education of Complex Trajectory Processing Technology and Equipment,Xiangtan University,Xiangtan,Hunan,411105 2.National NC System Engineering Research Center,Huazhong University of Science and Technology,Wuhan,430074

In NC machining, tool-path was usually expressed by micro-line shocks, which might result in the magnitude of the cutter location(CL)points whose trajectory was unsmooth. The CL points were fitted into Akima spline curve with its advantages of smooth junction and the node points for over G1-continuity,thus the Akima curve-fitting algorithm preserving convexity for tool-path was proposed based on arc-length parameters. The algorithm was divided into two stages including CL points’ searching and curve fitting. Firstly the features of CL points, the error testing constraints including bi-chord error tests and tangent error tests for fitting the tool trajectory were used to judge the adjacent CL points by the threshold of the testing constraints, if they were satisfied with the threshold continue to search the next tool location point(TLP), otherwise, CL points’ searching might be suspended and the first and end points of the segment were attained, then the tangent vectors were calculated according to the first and end points in this segment to ensure the concavity and convexity of the fitted curves, and the arc-length was used to parameterize the CL points ,so that a section of Akima spline between the adjoining CL points which had paused to searching were generated. When this segment of Akima curve fitting was accomplished, then the end point of the section was regarded as the first point of the next section, as the circle to the end. The model of the shoe sole(consists of 75 CL points) were generated by ultilizing UG software. The different testing thresholds were set up to compare the Akima curves whose arc-length was parameterized with the Akima curves whose knots were parameterized and NURBS curves based on MATLAB programming and simulation experiments were used to validate effectiveness of the algorithm.

micro-line shock; Akima algorithm; arc-length parameter; bi-chord error test; tangent error test

2016-08-25

国家自然科学基金资助项目(51375419，51575466，51575210)；湖南省自然科学联合基金资助项目(2017JJ4053)；湖南省教育厅创新平台资助项目(17K091)

TH-39

10.3969/j.issn.1004-132X.2017.24.005

(编辑华中平)

周鹏，男，1991年生。湘潭大学复杂轨迹加工工艺及装备教育部工程中心硕士研究生。主要研究方向为样条拟合、三维造型。吴继春(通信作者),男,1979年生。湘潭大学复杂轨迹加工工艺及装备教育部工程中心博士、副教授。E-mail:xlzy888@163.com。周会成,男,1974年生。华中科技大学国家数控系统工程技术研究中心副教授。杨世平,男,1970年生。湘潭大学复杂轨迹加工工艺及装备教育部工程中心副教授。刘金刚，男，1979年生。湘潭大学复杂轨迹加工工艺及装备教育部工程中心副教授。马秋成，男，1964年生。湘潭大学复杂轨迹加工工艺及装备教育部工程中心教授。