森林景观斑块耦合网络节点数与网络结构稳定性之间的关系

李 锐 ，李际平 ，高 宇 ，陈 磊 ，张利利

（1.国家林业局 中南林业调查规划设计院，湖南 长沙 410014；2.中南林业科技大学 林业系统工程实验室，湖南 长沙 410004；3.中国林业科学研究院 亚热带林业实验中心，江西 分宜 336600）

森林景观斑块耦合网络节点数与网络结构稳定性之间的关系

李 锐1，2，李际平2，高 宇2，陈 磊2，张利利3

（1.国家林业局 中南林业调查规划设计院，湖南 长沙 410014；2.中南林业科技大学 林业系统工程实验室，湖南 长沙 410004；3.中国林业科学研究院 亚热带林业实验中心，江西 分宜 336600）

以森林景观斑块耦合体为研究对象，利用复杂网络将之抽象化为森林景观斑块耦合网络。选择节点数不同的10个网络，依次对网络进行攻击，利用最大子网节点数与移除比例做回归分析，得每个网络的崩溃阈值。利用网络节点数与网络的崩溃阈值构建与节点数相关的森林景观斑块耦合网络结构稳定性模型，并对模型进行分析。结果表明：从巨型网络-1到微型网络-2的崩溃阈值依次为0.325 9，0.310 1，0.283 4，0.273 0，0.248 4，0.215 9，0.194 5，0.196 2，0.158 3，0.157 4，呈递减趋势，说明森林景观斑块耦合体中斑块数越多，其结构越稳定，并通过模型验证这一结论；随着网络节点数的增加，其崩溃阈值增加的速率逐渐减小的，说明当斑块数增加到一定程度时，耦合体的结构稳定性不再变化。根据复杂网络结构特征，用网络的节点数来衡量网络的结构稳定性，进而从新的角度探究森林景观结构的稳定性。

森林景观；耦合网络；节点数；结构稳定性

当前对于森林系统稳定性的研究主要以森林景观稳定性的研究为主，森林景观作为介于区域和生态系统之间的尺度，具有明显的时空区域[1-2]。由于在对斑块演化的研究中还没有较为系统的方法，到目前为止，大部分的研究都局限于提出多样的景观模型来对景观进行定性的研究[3]，这些研究往往只能判定景观的现状或是表象，并无法深入探究景观演变的机理。在景观系统中，森林景观是景观生态学研究的重点，现有森林景观研究主要偏重于景观格局的分析，一般从时间或空间上分析森林景观系统的稳定性[4]，鲜有从系统的角度考虑森林稳定性的。而从定量的角度研究森林稳定性往往限于局部范围内研究单一林分的稳定性[5-9]。

森林景观的组分具有耦合关系，并表现出高度的复杂性，现已更多地被作为一个整体系统来考虑，构成对研究森林可持续发展与管理的最适宜空间尺度[10-11]。目前对森林的经营一般是采取大范围集约经营，提出以森林景观斑块为单元的经营方式正是这样环境下的结果。赵春燕等[12]利用边缘效应来评价斑块之间的差异，李际平、袁晓红等[13]利用复杂网络将森林景观抽象化为网络，利用网络的特性来判定森林系统的稳定性，发现森林景观斑块耦合网络具有较强的鲁棒性但脆弱性也较高。本研究利用湖南省桃源县森林资源二类调查成果构建森林景观斑块耦合网络10个，分别对其节点进行攻击，构建与节点数相关的网络稳定性模型，并对模型进行分析，揭示网络稳定性与节点数之间的关系，旨在为今后研究大区域的森林系统稳定性提供一种新的思路。

1 数据来源

1.1 构建森林景观斑块耦合体的条件

耦合体是由斑块组成，内部具有连续性同时外部具有阻隔性的较为封闭的系统。构建的条件有：（1）内部的斑块具有连续性，每个斑块至少有一个斑块与之相连；（2）耦合体的外部具有阻隔性，即耦合体与耦合体之间必定没有斑块相连；（3）在耦合体内部允许“空洞”的出现，即耦合体内部可以出现斑块的缺失。在研究区内将现有的景观类型重新可以划分为阔叶林景观、松木林景观、杉木林景观、经济林景观、竹林景观和灌木林景观，将龄组分为幼龄林、中龄林和成熟林，竹林，经济林和灌木林不作划分，划分结果见表1。

1.2 基于邻接关系构建森林景观斑块耦合体

以湖南省桃源县森林资源二类调查成果为基础，在林相图中利用地理信息系统软件Arcgis10.0将非林地、道路、采伐迹地等小班删除，按照表1的划分规则将小班重新划分为松木幼龄林、松木中龄林、松木成熟林、杉木幼龄林、杉木中龄林、杉木成熟林、阔叶幼林林、阔叶中龄林、阔叶成熟林、竹林，灌木林和经济林。对相同的小班进行合并，得到新的斑块。如图1所示，小班②③（图中粗黑线所示）均代表阔叶中龄林，④⑤（图中黑色间隔线所示）则代表杉木幼龄林，小班合并之后分别得到图2中新斑块A和B，这些由新斑块构成并相互连续，形成闭合区域的斑块集合即为森林景观斑块耦合体。本研究遵循先易后难的原则，对于斑块与斑块之间的边缘效应暂不考虑，先默认相邻斑块之间的边缘效应都极显著。

表1 景观类型分类Table 1 Classification of landscape types

1.3 耦合体抽象化为耦合网络

图1 小班融合前Fig.1 Not merged sub-compartment

图2 小班融合后Fig.2 Merged sub-compartment

从构建的耦合体中选取斑块数不同，且外形大致相同的耦合体10个。针对所选的森林景观斑块耦合体如图3，利用地理信息系统软件Arcgis10.0和复杂网络软件Pajek，将之抽象化为森林景观斑块耦合网络如图4。在耦合网络中，每一个节点都对应斑块的几何中心，每一条边表示斑块之间相互连接，斑块之间的边缘效应都极显著，默认为节点之间的边权都为1，这样能很好地表示斑块与斑块之间的空间位置关系，也便于计算。

图3 森林景观斑块耦合体Fig.3 Forest landscape patch coupling system

2 研究方法

2.1 对网络进行攻击，判断网络崩溃范围

图4 森林景观斑块耦合网络Fig.4 Forest landscape patch coupling network

森林景观类型越丰富，斑块数越多，越有利于生态系统内的植物生长与动物的迁徙，加速生境内的能量流动，其生态系统也会更加稳定[14-15]。对于森林景观斑块耦合网络，在确定景观类型不变的情况下，其网络的节点数越多，网络结构越稳定，因此将网络节点的规模作为评判网络的结构稳定性的一方面标准。

（1）节点数

在森林景观耦合网络G=（N，E），N为网络中的节点数，E为点与点之间的边缘效应。本研究中网络均为无标度的无权网络，所以点与点之间的权重全部为1，利用网络节点数N作为评判网络稳定性的标准。

（2）最大子网

在对网络节点攻击后，会产生很多孤立的节点和凝聚子群，在每次攻击后剩下包含最多节点数的凝聚子群称为最大子网，其最大子网节点数公式（1）为：

式（1）中：Nn为第n次移除节点后最大子网剩下的节点数，m为n+1次移除节点后剩下凝聚子群的个数，Li为凝聚子群中节点数，G为n+1次移除节点后剩下的孤立节点个数。

（3）网络崩溃阈值

在一个网络G中，随机的移除k比例的点，即Nk个节点，当移除的比例达到k=kn时，网络临界崩溃，称k为网络崩溃阈值。本研究中当最大子网的节点数小于或等于原网络节点数的一半时认为网络崩溃。

选择巨型（节点数大于等于1 000）、大型（节点数小于1 000且大于等于200）、中型（节点数小于200且大于等于100）、小型（节点数小于100且大于等于50）和微型（节点数小于50）[16]耦合网络各2个，对10个网络按原网络节点数的5%递推移除，每个网络攻击3次，攻击流程如图5。分析网络节点数在不同攻击水平下的变化情况，判断各类型网络在何种水平的攻击下容易崩溃。

图5 网络攻击流程Fig.5 Flow chart of attacks

2.2 判断最大子网节点数与移除比例之间的关系

利用统计学软件SPSS对最大子网节点数与移除比例做回归分析，选择拟合效果最好的模型，得到最大子网节点数与移除比例的回归方程组，令网络崩溃节点数等于最大子网节点数，以此求得10个网络的崩溃阈值，并分析节点数对网络结构稳定性的影响。

2.3 构建与节点数相关的网络结构稳定性模型及验证

将网络节点数与网络崩溃阈值做回归分析，通过判定系数R2选择拟合效果最好的模型，构建与节点数相关的网络结构稳定性模型，并对模型进行分析。选择一个中型耦合体，在原有斑块数的基础上每次增加20%的斑块数，连续增加3次，通过构建的与节点数相关结构稳定性模型分别计算相应的崩溃阈值，通过分析比较验证模型的正确性。

3 结果与分析

3.1 网络节点数在不同水平攻击下的变化情况

在实验中选择10个森林景观斑块耦合网络，对每个网络逐步移除原有网络5%的节点，每个样本攻击3次，最大子网节点数的变化情况如表2所示。

表2 攻击后最大子网节点数的变化Table 2 The change of the largest subnet vertices after attacking

续表2Continuation of table 2

由表2可以看出巨型耦合网络的崩溃阈值在30%～35%之间，大型耦合网络的崩溃阈值在25%～30%之间，中型耦合网络的崩溃阈值在20%～25%之间，小、微型耦合网络的崩溃阈值在15%～20%之间，说明网络的崩溃阈值与网络的节点数呈现正相关。

在网络崩溃后，继续对其进行攻击，网络崩溃的速率会大大加快。例如图6中型网络-1在对其移除30%的节点后，剩余节点为53，在对其移除35%的节点后如图7，剩余节点数为22，这一过程中产生了4个凝聚子网（蓝色）和15个孤立的节点（绿色）。其原因是在网络崩溃后，最大子网破碎化程度很高，部分节点的介数极高，这类节点往往成为连接子网和凝聚子群的关键节点，如图中6中的17、19和50号节点（黄色）。随着子网的节点数的减少，在相同移除比例的情况下，会大大增加移除这类节点的概率。当随机移除这类节点时，子网与凝聚子网之间的“桥梁”发生断裂，此时网络的节点数会急剧下降。在森林经营过程中，尤其针对是人工用材林，当木材成熟后，会对成熟林进行大面积的采伐，随着采伐的进行，部分幼龄林和中龄林就会成为关键节点对应的斑块，此时若这些斑块发生大面积的病虫害或冻害，使得这些关键斑块中的林木活力降低，从而影响耦合体内的能量、物质的循环，耦合体会迅速崩溃，甚至导致耦合体消失，对森林系统的稳定产生巨大的影响。

图6 中型网络-1移除30%节点后Fig.6 After removing 30% vertices of the medium network-1

图7 中型网络-1移除35%节点后Fig.7 After removing 35% vertices of the medium network-1

3.2 节点数对网络结构稳定性的影响

由3.1已知网络的结构稳定性与节点数呈正相关，因此利用统计学软件SPSS对最大子网节点数与移除比例做回归分析，通过对判定系数R2的比较选择回归效果最好的三次回归模型。对所选择的十个网络的最大子网节点数与移除比例分别做三次回归，得到方程组（2）。

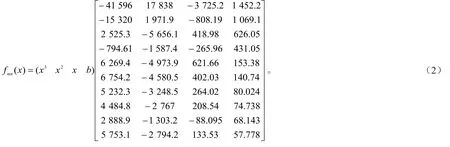
式（2）中，fmn(x)为最大子网的节点数，m为不同网络类型，n为同一类型中的不同网络，x为整个网络移除节点的比例，b为方程的常数项，且b=1。利用Matlab对10个方程进行绘图，得到最大子网节点数与移除比例的方程曲线图8。

图8 最大子网节点数与移除比例方程曲线Fig.8 The graph of equation between the largest subnet vertices number and removed scale

由图8可以看出对于任意一网络来说，其最大子网的节点数与移除比例呈负相关。对于不同的网络来说，当最大子网的节点数等于网络崩溃节点数时，其相对应的移除比例也不同，此移除比例即为网络的崩溃阈值。将上述网络的崩溃节点数带入上述最大子网络节点数与移除比例的三次方程中计算，得到网络崩溃阈值依 次 为 0.325 9，0.310 1，0.283 4，0.273 0，0.248 4，0.215 9，0.194 5，0.196 2，0.158 3，0.157 4，呈递减趋势，说明网络的崩溃阈值随着网络节点数的增大而逐渐增大。

3.3 构建网络结构稳定性模型及验证

（1）构建与节点数相关的网络结构稳定性模型

将节点数与网络崩溃阈值做回归分析，发现指数回归模型的拟合效果最好，其R2=0.991 2。得到节点数与网络崩溃阈值之间的方程（3）即为与网络节点数相关的结构稳定性模型，利用Matlab作方程曲线如图9。

式（3）中：g(x)为网络的崩溃阈值，x为网络的节点数，此函数为递增函数，根据本研究所取样本设定x的取值范围，即50≤x≤1 385，在此范围内研究森林景观斑块耦合网络的崩溃阈值。

由图9结合方程（3）可知网络崩溃阈值与节点数呈正相关，主要原因是在研究节点数与网络结构稳定性的关系时，所选耦合体都为外形规整，大多是方形或圆形，这样其网络节点呈散状均匀分布，节点介数分布也较为均匀。当网络受到一定程度攻击时，耦合体的外形不再是规整的形态，部分节点的介数极高，此时若随机移除这些节点时，网络会迅速崩溃。网络节点数越多所对应的斑块数也越多，实际上是包含了更多的斑块，会使得巨、大型耦合体中的斑块相互之间“接触”更多，对应节点之间的“桥梁”也越多，其结构越稳定。

图9 与节点数相关的网络结构稳定性模型曲线Fig.9 The model curve of related the number of vertices tostructure stability of network

方程（3）为递增函数，其导函数为递减函数，说明随着节点数的增加，崩溃阈值虽然在增加，但其增加的速率却是逐渐减小的。在x的取值范围内任取以值a，令x=a，当x在50～a之间时，g(x)增加较快，x在a～1 385之间时，g(x)增加缓慢。对一个节点数为N耦合网络进行攻击，若网络节点数较多，则该网络中节点成为关键节点的概率会较小，若网络节点数较少，则该网络中节点成为关键节点的概率会大大增加，在相同移除比例k下，节点数少的网络包含更多的关键节点，往往会先崩溃。因此随着节点数的增加，网络崩溃阈值增加的速率会逐渐降低。对于森林系统来说，在对某些斑块中林木进行一定强度采伐后，导致各斑块不再相邻，进而影响了斑块之间物种、基因交流，使得动植物的迁徙受阻，导致降低森林中物种多样性，整个森林能量、物质流动缓慢，活力不高。此时若继续对森林中关键斑块中的林木进行采伐，整个森林的恢复力会有急剧的下降，森林系统很快就会崩溃。

（2）验证网络结构稳定性模型

根据上述与节点数相关的网络结构稳定性模型，在森林景观斑块耦合网络中增加外部节点数实际上就是增加与之相邻的斑块数。如图10所示，在一个斑块数为100的森林景观斑块耦合体中，将林缘荒地重新种植幼树，每年增加原有斑块数20%的斑块，连续增加3年，最后斑块数为160，并保证增加的过程中始终是增加林缘相邻的斑块。根据网络节点数相关的结构稳定性模型（3）可知当斑块数为100时，网络的崩溃阈值为0.193 2，当斑块数连续增加时，相应的崩溃阈值为0.202 4、0.210 2和0.217 0，经过优化后其崩溃阈值提高了0.023 8，增强了耦合体的抗毁能力，说明对于一个外形规整的森林景观斑块耦合体，增加其林缘斑块数可以提高森林系统的稳定性。

图10 增加斑块数的森林景观斑块耦合体Fig.10 Increased the number of patches of forest landscape patch coupling system

4 结论与讨论

对森林景观斑块耦合网络节点进行移除，当最大子网节点数等于网络崩溃节点数时，通过最大子网节点数与移除比例的方程组可以计算各网络的崩溃阈值，发现网络的崩溃阈值与网络节点数呈正相关，说明增加森林景观耦合体的斑块数可使其结构越稳定。通过与节点数相关的网络结构稳定性模型可看出，随着节点数的增加，其网络崩溃阈值的增加的速率却是逐渐减小的。说明当耦合体的斑块数增加到一定程度后，其结构稳定性保持不变。因此在现实森林中对耦合体进行经营时，应根据地形地貌选择合适的耦合体斑块数，既做到斑块数最大化的集约经营从而保证耦合体的结构稳定性，又做到耦合体的分散保证不必要浪费人力物力，使得森林稳定性达到最优化。

在研究节点数与网络结构稳定性之间的关系时，所选用的最大网络的节点数为1 385，因此方程（3）中x的取值最大也为1 385，方程（3）为连续递增函数，但是显然网络的崩溃阈值不会随着节点数x的增加而无穷增加，因此可以推断当节点数增加到某一范围时，崩溃阈值是不会再增加的，但节点数究竟增加到何种程度最佳，还需要节点数更多的样本。因此在下一步的研究中应该选取更大范围内的森林资源二类调查数据，构建节点数更多的网络，以完善与节点数相关的网络结构稳定性模型。

[1] 郭江泓,柴立和. 景观斑块演化的动力学机理和数值模拟[J].科技导报,2008,26(11):65-69.

[2] 宋 涛. 基于GIS的森林景观格局适宜粒度研究[D]. 长沙:中南林业科技大学,2009.

[3] 杨珍珍, 白淼源. 基于GIS的大兴安岭呼中森林景观格局分析[J]. 东北林业大学学报, 2010, 38(9):40-43.

[4] 赵华萍,戴少伟,鄢 蓉. 景观生态学在城市园林建设中的应用进展[J]. 绿色科技,2014(9):144-146.

[5] 刘 彦, 余新晓, 岳永杰,等. 北京密云水库集水区刺槐人工林空间结构分析[J]. 北京林业大学学报, 2009, 31(5):25-28.

[6] 赵洋毅, 王克勤, 陈奇伯,等. 西南亚热带典型天然常绿阔叶林的空间结构特征[J]. 西北植物学报, 2012, 32:187-192.

[7] 陈端吕,李际平,林 辉. 森林景观研究的3S技术应用[J].长江大学学报(自科版),2006,3(3):131-134.

[8] 郭晋平,张芸香. 中国森林景观生态研究的进展与展望[J].世界林业研究,2003,5(16):46-49.

[9] 巫志龙, 周成军, 周新年,等. 杉阔混交人工林林分空间结构分析[J]. 林业科学研究, 2013(5):609-615.

[10] 陈端吕, 李际平, 陈哲夫. 森林景观“斑块耦合网络”视角下森林经营的思考[J]. 西北林学院学报, 2015,30(5):268-272.

[11] 赵春燕, 李际平, 郑 柳.“森林景观斑块耦合体”的构建研究[J]. 中南林业科技大学学报, 2014, 34(7):41-44.

[12] 赵春燕. 森林景观斑块边缘效应和耦合机理研究[D]. 中南林业科技大学, 2012.

[13] 袁晓红. 森林景观斑块耦合网络及动力学研究——以西洞庭湖区为例[D]. 长沙:中南林业科技大学, 2012.

[14] 陈端吕,李际平. 共生竞争、功能匹配与协调稳定：森林景观斑块耦合网络的形成演化[J]. 中南林业科技大学学报,2014,34(7):32-35.

[15] 丁惠萍,张社奇,钱克红,等. 森林生态系统稳定性研究的现状分析[J]. 西北林学院学报, 2006, 21(4):28-30.

[16] 李 锐,李际平,袁晓红,等.森林景观斑块耦合体的筛选及特征分析研究[J].林业资源管理, 2015,5(10):88-94.

Relationship between number of vertices in forest landscape patch coupling network and stability of network structure

LI Rui1,2, LI Jiping2, GAO Yu2, CHEN Lei2, ZHANG Lili3
(1. Central South Forest Inventory and Planning Institute of State Forestry Administration, Changsha 410014, Hunan, China; 2. Laboratory of Forestry Systems Engineering, Central South University of Forestry & Technology, Changsha 410004, Hunan, China; 3. Subtropical Experimental Center, Chinese Academy of Forestry, Fenyi 336600, Jiangxi, China)

Taking forest landscape patch coupling systems as the research objects, which were abstracted into forest landscape patch coupling networks. Choose 10 networks with different number of vertices, ordinal attacked on networks, when used the largest subnet number of vertices and removed ratio to do regression analysis, each network breakdown threshold would get. Using the number of vertices in the network and the network breakdown threshold build related to the number of vertices of forest landscape plaque stability coupling network structure model, and analyze the model. Results showed that: From the giant network -1 to tiny network-2, values of breakdown threshold were 0.325 9, 0.310 1, 0.283 4, 0.273 0, 0.248 4, 0.215 9, 0.194 5, 0.196 2, 0.158 3 and 0.157 4, showed a trend of decline, the more plaques in the forest landscape patches coupling, the more stable its structure was, and this conclusion was validated by model; With increased of the number of network vertices, increased rate of the breakdown threshold value was decreased gradually,when plaque numbers increased to a certain extent, the structure stability of the coupling system no longer changed. According to the characters of complex network structure, number of vertices in the network was used to measure the structural stability of the network,and then from a new perspective to explore the forest landscape structure stability.

forest landscape; coupling network; number of vertices; structural stability

S718.5

A

1673-923X(2017)08-0034-08

10.14067/j.cnki.1673-923x.2017.08.007

2016-12-22

国家自然科学基金面上项目“森林景观斑块耦合网络特性与结构优化机理研究”（31470642）

李 锐，助理工程师

李际平，教授，博士生导师；E-mail：lijiping@vip.163.com

李 锐，李际平，高 宇，等.森林景观斑块耦合网络节点数与网络结构稳定性之间的关系[J].中南林业科技大学学报，2017, 37(8): 34-41.

[本文编校：文凤鸣]