明渠非恒定流的一维浅水波与三维VOF耦合模拟*
2017-12-28张晓曦张春泽陈秋华
张晓曦,张春泽,陈秋华
(1. 厦门理工学院 环境科学与工程学院,福建 厦门 361024; 2. 重庆交通大学 重庆西南水运工程科学研究所,重庆 400074;3. 厦门理工学院 土木工程与建筑学院,福建 厦门 361024)
明渠非恒定流的一维浅水波与三维VOF耦合模拟*
张晓曦1,张春泽2,陈秋华3
(1. 厦门理工学院 环境科学与工程学院,福建 厦门 361024; 2. 重庆交通大学 重庆西南水运工程科学研究所,重庆 400074;3. 厦门理工学院 土木工程与建筑学院,福建 厦门 361024)
提出了一种一维浅水波与三维VOF模型耦合的明渠非恒定流数值计算方法。此方法通过建立两个计算模型间变量的数学关系,实现由三维区域为一维区域提供流量,一维区域为三维区域提供压强和水体体积分数分布。用耦合方法模拟了矩形断面渠道增、甩负荷两种典型非恒定工况,将结果与一维浅水波模型计算结果对比,表明本方法在定性上正确,在定量上准确度也较高。最后利用这一方法模拟了某水电站带引水渠压力前池的非恒定流现象,获得了最大溢流量、最高和最低水位等重要参数。耦合方法同时结合了一维模型计算较细长明渠渐变流的效率和三维方法模拟局部明渠急变流的准确性,可为分析工程中复杂的明渠流动问题提供更优选择。
水利工程;明渠非恒定流;数值模拟;一维与三维耦合
0 引 言
明渠内任意一点的水位和流量随时间变化的流动被称为明渠非恒定流,如水电站工况调节在引水渠中激发的涌浪。这类涌浪对水电站的运行一般是有害的,如降水幅度过大可能导致与明渠衔接的压力管道进气,涌水幅度过大可能引起管道压力超标,而水位和流量的交替变化则可能激发拦污栅和闸门等水力设施的振动等。因此,准确计算明渠非恒定流对水电站的设计和安全性评估具有重要意义。
到目前为止,一维和二维浅水波模型是计算明渠非恒定流的主要模型,也是研究水电站无压引水系统涌浪的重要工具。例如:崔伟杰等[1]利用一维浅水波模型计算了某水电站长引水明渠的水力过渡过程并探讨了压力前池的数值计算方法;王明疆等[2]将这一模型线性化并计算了某水电站尾水明渠的小波动过渡过程;ZHANG Chuhze等[3]利用二维浅水波模型求解了梯级电站的衔接明渠段在电站工况转换时的非恒定流现象,分析了部分机组甩负荷对其他机组的水力干扰。综上,浅水波模型的应用形式多样,计算效率高,基本可满足大部分工程设计的需要。但这一类模型在推导过程中用到了一系列的简化和假设,如只能用于渠道底坡接近于水平的情况、假设流速沿水深均匀分布以及压力沿水深为静压分布等渐变流条件[4],而不适用于诸如大底坡、急转弯以及存在垂向流动等急变流情况。
为了研究明渠非恒定急变流,近年有学者开始尝试用三维计算流体力学方法中能模拟自由水面的VOF(volume of fluid,流体体积分数)模型模拟此类问题。例如:CHENG Yongguang等[5]模拟了某变顶高尾水洞明满流非恒定过程,探索了明满流界面处滞留气团生成、发展及溃灭机制;杨建东等[6]模拟了某水电站尾水洞与导流洞结合段的流动,分析了非恒定过程中尾水洞内水流中断机理;朱方磊等[7]模拟了明渠衔接竖井的水电站的明渠非恒定流现象,探讨了明渠断流和明满流发生的条件。综上,三维方法适用于各种复杂流动条件且可获得较准确的流场细节,应用潜力较传统一维方法大。但此类方法的短板同样显著,即所耗费的计算机资源(内存容量和CPU计算时间)较大,目前尚难以全面应用于解决工程问题。
笔者旨在提出一种将一维浅水波与三维VOF模型耦合的明渠非恒定流计算方法,充分结合一维方法模拟细长渠道渐变流的效率和三维方法模拟局部急变流的准确性,为解决工程问题提供更优选择。
1 数学模型及验证
1.1 计算区域划分
用耦合方法模拟明渠非恒定流的基本思路是将计算区域按流态分为两部分,渐变流区域(如棱柱形渠道、无压管道或隧洞等)采用一维方法求解,急变流区域(如压力前池、进/出水口和渠道分岔口等区域)采用三维方法求解,两个计算区域通过耦合边界实时传递数据,如图1。这里三维区域采用VOF模型,一维区域采用浅水波模型,下面具体介绍这两个模型和耦合格式。

图1 一维与三维耦合计算区域示意Fig.1 Schematic diagram of 1D and 3D coupling computational domain
1.2 三维VOF模型
VOF(volume of fluid)模型[8]是一种模拟多种互不穿透流体界面的方法。对于水气两相流而言,其基本思想是定义函数α表示计算网格内水流所占的比例,若α=1表示该网格完全被水充满,α=0表示该网格完全被气充满,0<α<1则表示该网格内存在水气界面。其连续性方程为

(1)
式中:u为流速;t为时间;x为坐标。在这一模型中,水相和气相有相同的速度场和压力场,动量方程为

(2)
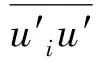
以上即为VOF模型的基本控制方程,通过现有的算法(如SIMPLE、SIMPLEC或PISO算法等),再结合模拟雷诺应力项的湍流模型(如k-ε、k-ω或LES模型等),即可方便求解。
至于边界条件,这里假设上游边界流量(流速u)变化已知,下游(耦合边界)则由耦合格式给出压力p和水体体积分数α的分布规律。
1.3 一维浅水波模型
一维浅水波模型是描述一维明渠非恒定流的基本模型,包括连续性方程和动量方程[4]:

(3)
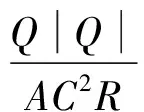
(4)
式中:Z为水位;Q为流量;B为渠道水面宽度;s为渠道长度坐标;A为过流断面面积;g为重力加速度;C为谢才系数;R为水力半径。
笔者采用显格式有限差分法求解,差分网格如图2。对于内节点,空间项采用二阶中心差分格式,时间项采用一阶差分格式,可将式(3)和式(4)转化为差分方程式(5)和式(6)。
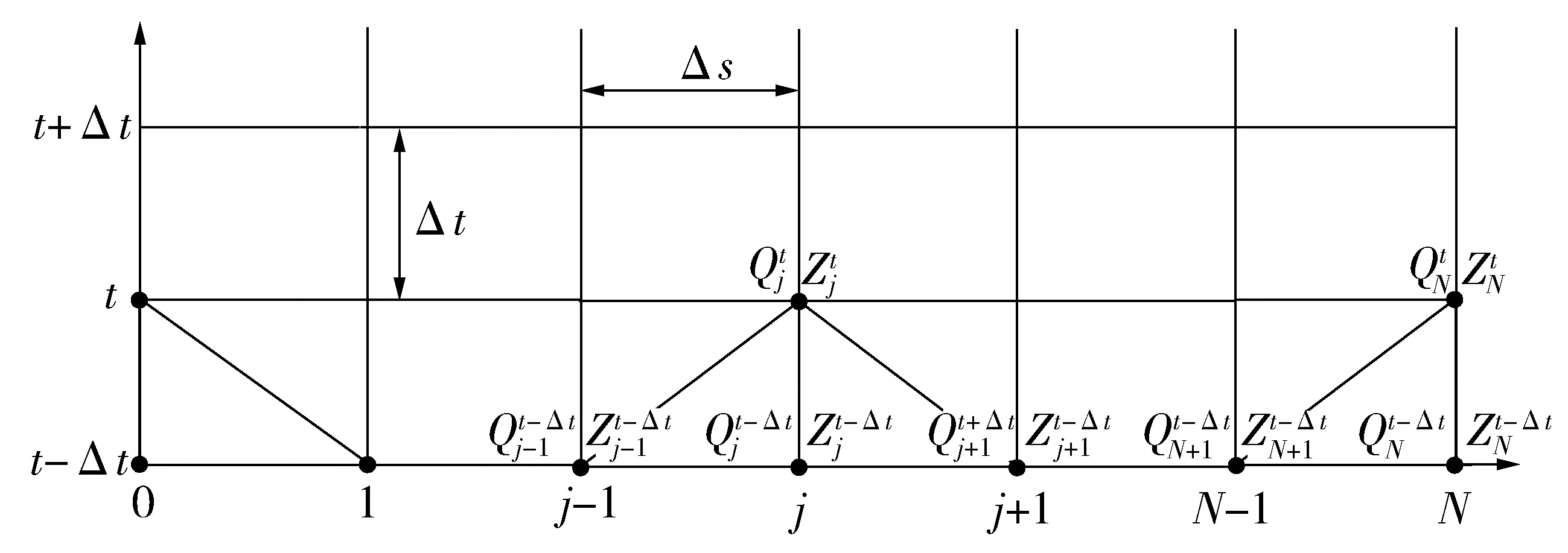
图2 一维有限差分网格示意Fig.2 Schematic of 1D finite difference mesh
(5)
(6)
式中:α为权重系数(这里取为0.33);Δt表示时间步长;Δs表示空间步长;is表示渠道坡度,变量的上标表示时间,下标表示差分网格节点编号。
这里假设下游边界(节点N)水位条件已知,空间项采用一阶向后差分得流量的差分格式如式(7),上游(耦合边界)边界由耦合格式给出水位Z0和流量Q0的表达式。
(7)
1.4 耦合格式
通过以上对一维和三维区域的模型和算法分析可知,耦合边界需实时给出三维区域下游压强p和水体体积分数α的分布,以及一维区域上游水位Z0和流量Q0。笔者给出一种计算格式,流程图如图3。此格式基本思想是三维区域为一维区域提供流量,一维区域为三维区域提供压强和水体体积分数分布。需要注意的是,耦合边界必须同时满足一维与三维的流动特点,即耦合边界为渐变流态。

注:变量上标表示时间,下标表示边界(三维区域)或节点编号(一维区域)图3 耦合格式流程Fig.3 Flow chart of the coupling scheme
1.5 数值验证
为了验证上述耦合格式,这里采用耦合方法模拟图1所示细长渠道的非恒定流,并将结果与一维浅水波模型的计算结果对比。计算区域总长100 m,断面为宽4 m的矩形,底坡为平坡,其中上游侧50 m用三维VOF模型模拟,下游侧50 m用一维浅水波模型计算。渠道初始为恒定流,流量为10 m3/s,水位为5 m。这里模拟两个工况,甩负荷和增负荷工况:甩负荷工况时,上游闸门逐渐关闭,流量在10 s内线性降到0;增负荷工况时,上游阀门逐渐开启,流量在10 s内线性增加到20 m3/s,在这两个过程中下游水位始终保持5 m不变。
结果表明文中一维浅水波与三维VOF耦合方法可以较为准确的模拟明渠涌浪。图4为甩负荷和增负荷工况渠道中点(耦合边界)流量和水位变化过程,其中实线为一维计算结果,虚线为耦合计算结果,两者吻合较好。表1对比了两种方法所得的涌浪周期、第一周期内水位极值和流量极值,可见除了甩负荷过程最大流量误差稍大外(相对误差为14.32%),其他关键数据的相对误差均小于5%。另外,以上结果也显示出耦合方法所得波动的衰减要稍强于一维方法,这种现象一方面是由于三维方法在离散时引入的数值耗散要高于一维方法,另一方面则是因为一维水流在简化过程中忽略了竖向和横向能量耗散,阻尼稍小。综上,文中耦合方法模拟细长渠道非恒定流的结果在定性上与一维方法一致,定量上与一维方法的差别也不大。考虑到一维方法已经过大量的工程实践检验,这里认为本耦合方法也是正确且较准确的。
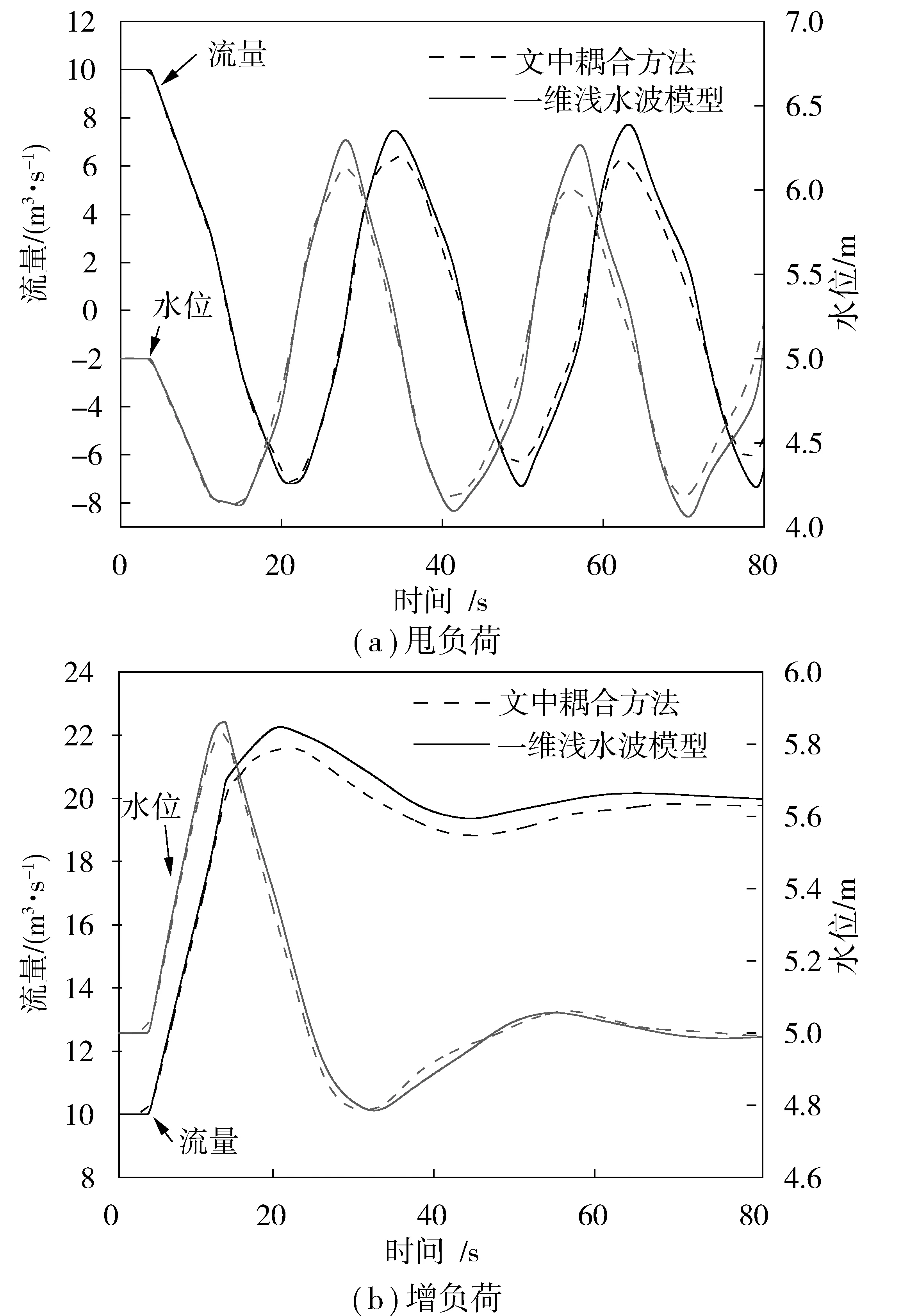
图4 两种计算方法所得明渠流量和水位随时间变化过程对比Fig.4 Comparison of the flow and water level of open-channelobtained by two calculation methods changing with time

T/sZmax/mZmin/mQmax/(m3·s-1)Qmin(m3·s-1)一维浅水波29.1/41.06.30/5.864.13/4.797.47/22.26-7.20/19.37耦合方法27.8/42.86.13/5.834.14/4.796.40/21.60-7.15/18.83绝对误差-1.3/1.8-0.17/-0.030.01/0-1.07/-0.660.05/-0.54相对误差/%4.68/4.212.70/0.510.24/014.32/2.960.69/2.79
注:表中T表示涌浪周期,Zmax和Zmin分别表示第一周期内最高和最低水位,Qmax和Qmin分别表示第一周期内最大和最小流量,绝对误差是耦合算法与一维方法结果的差值,相对误差为绝对误差的绝对值与相应一维结果的比值。
2 水电站带引水渠的压力前池非恒定流模拟
压力前池是引水式水电站引水明渠与压力钢管结合处加宽、加深的水池,在池壁上还设置有溢流堰。这一结构一方面可以降低拦污栅处的水流流速,起到减小水头损失和沉淀来流杂质的作用,更重要的是在电站发生过渡过程时可以宣泄多余水流,控制压力钢管的最大压力。图5为某电站的压力前池及其附属结构示意图,这里由引水渠从上游水库引水,来水经弯道扩散段进入压力前池内,在池壁设有WES型溢流堰。其中引水渠长81 m,上游水库额定水位为7.5 m,溢流堰顶高程为8.5 m。这里需要计算在最不利的双机同时甩负荷的情况下压力前池的水位波动过程,以判断在最高水位时侧堰溢流量是否满足设计要求,压力钢管强度是否达标,以及最低水位是否会导致压力钢管进气等。
这里采用一维与三维耦合的方法模拟压力前池在全甩负荷工况下的非恒定流。一维计算区域包括上游水库边界和约51 m长引水渠。三维计算区域包括压力前池、扩散段和部分引水渠(为保证一维与三维耦合边界为渐变流态,三维计算区域保留约30 m长引水渠,以尽量减弱扩散段对耦合边界流态的影响),如图5。
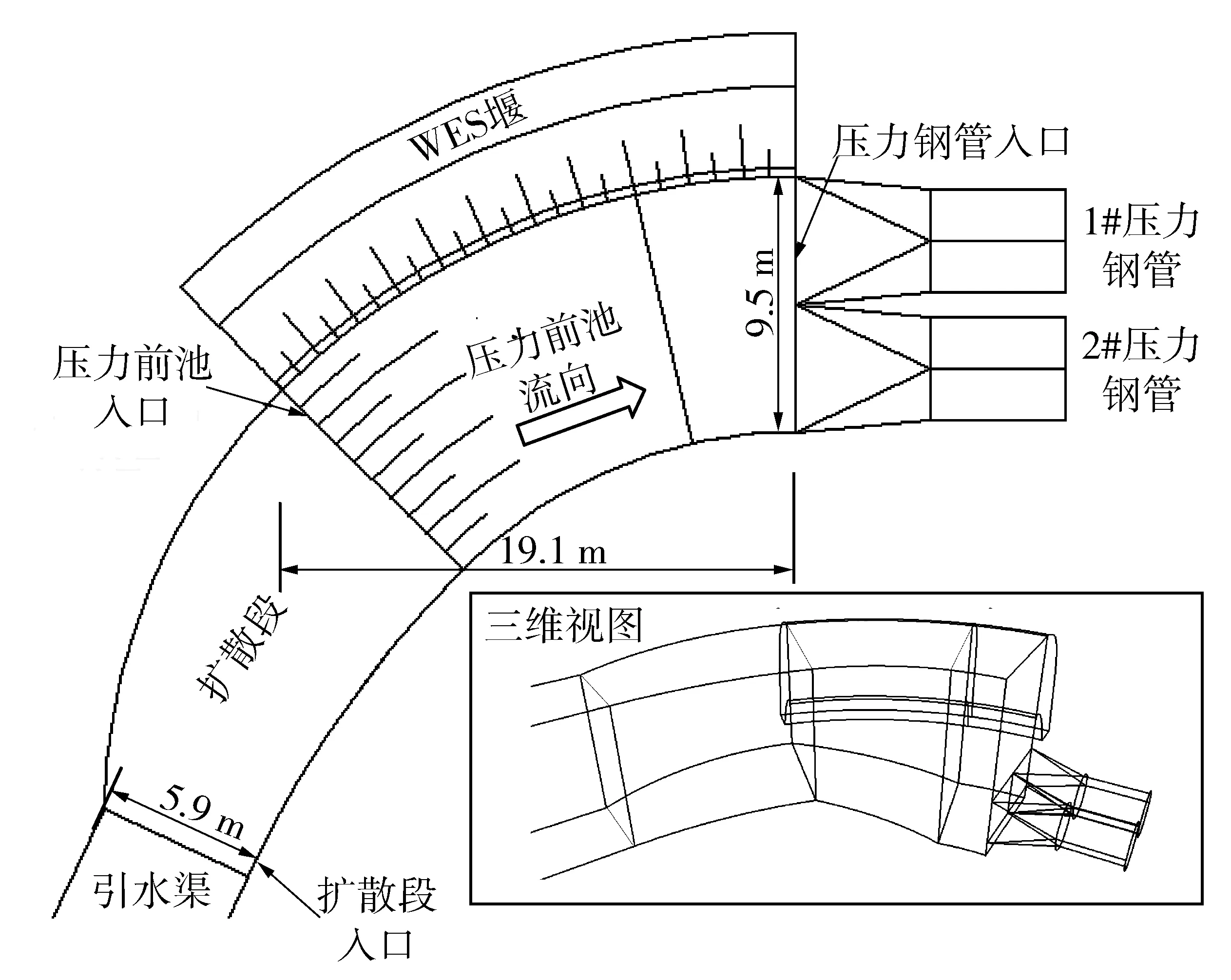
图5 某水电站压力前池体型示意Fig.5 Schematic diagram of the pressure fore bayof a hydropower station
全计算区域采用六面体和棱柱体混合非结构化网格离散,通过恒定流条件下的网格敏感性分析确定最终计算网格数约为110 000个。计算中用显格式VOF模型模拟自由水面,湍流模拟采用RNGk-ε双方程模型,计算格式采用模拟非恒定流较有优势的PISO格式,时间步长按照库朗稳定条件选为0.005 s。这里模拟两机全甩负荷这一最不利工况,即1#和2#压力钢管流量在5 s内由54 m3/s线性降低到0,在此过程中上游水库水位保持7.5 m不变。
甩负荷发生时,压力管道流量减小并在前池出现向上游传播的雍水波。在此过程中若池内水位高于溢流堰顶高程,则会发生溢流,以减缓池内水位上升。同时,由于过流断面在横向和纵向的扩散,池内流动的三维特性显著。图6为最高水位时前池内流线分布,可以看出此时前池内出现多个大范围回流区,这种流动用三维方法模拟显然比用传统一维方法更为准确。图7为甩负荷过程压力前池及其附属结构3个特征断面处水位和WES堰溢流量随时间变化过程,从中可以看出压力前池在恒定及非恒定工况下的流动特征。恒定流时,由于流动断面逐渐扩大,扩散段入口、前池入口和压力钢管入口的水位也逐渐升高,此时压力前池内的水位约为7.6 m。甩负荷后,压力钢管入口的水位首先上升并在池内形成雍水波。随着雍水波向上游传播,压力前池入口和扩算段入口的水位依次上升,在此过程中当池内水位高于堰顶高程时(约第16 s时刻)开始溢流(这里溢流量由溢流堰下部统计得出,因此变化略晚于池内水位)。之后在上游水库反射波到达前池后,在池内形成降水波,并向上游传播,出现周期性涌浪。通过本次模拟得出,在最不利甩负荷工况下压力钢管入口最大动水压力水头约为5.6 m(以钢管轴线高程为基准),最小淹没水深约为1.6 m(以进水口顶板高程为基准),溢流堰最大溢流量约为24 m3/s,均符合设计要求。
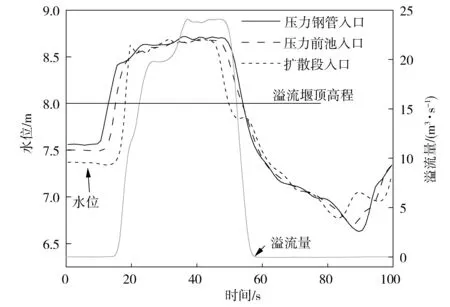
图7 压力前池特征断面水位和溢流量随时间变化过程Fig.7 Time history of water level and dischargein characteristic section of pressure fore bay
综上,由于压力前池体型特殊,内部水流流态,尤其是非恒定流态呈典型三维特征,用传统一维或二维方法无法准确模拟其水动力特性。笔者提出的一维浅水波与三维VOF模型耦合的方法既可准确考虑非恒定过程中压力前池内局部扩散、回流和溢流等复杂三维流态,又可计入引水渠中的水流惯性对局部流动的影响,所得特征参数的可信度更高。同时这一方法所消耗计算机资源和时间远小于全三维模拟,特别适用于解决实际工程问题,具有广阔的应用前景。
3 结 语
提出了一种一维浅水波与三维VOF模型耦合的明渠非恒定流数值计算方法,并在验证了其准确性的基础上模拟了某电站压力前池甩负荷涌浪过程。
这一方法可以充分结合传统一维模型计算较细长型明渠中渐变流的效率和三维方法模拟局部带自由水面急变流的准确性,为分析工程中复杂的明渠流动问题提供了新的途径。但笔者使用经过简化的数值解验证所提出的方法,不够精确,后续应通过更符合实际情况的高精度水力学模型试验对其进行更全面的验证。
[1] 崔伟杰,张健,陈胜. 某水电站压力前池不同模型过渡过程的计算对比[J]. 三峡大学学报(自然科学版),2016,38(4):36-39.
CUI Weijie,ZHANG Jian,CHEN Sheng. Calculation and comparison of transients of forebay with different models for a hydropower station[J].JournalofChinaThreeGorgesUniversity(NaturalSciences),2016,38(4):36-39.
[2] 王明疆,杨建东,王煌. 含明渠尾水系统小波动调节稳定性分析[J]. 水力发电学报,2015,34(1):161-168.
WANG Mingjiang,YANG Jiandong,WANG Huang. Analysis of stability of tailrace open channel in small fluctuation governing system[J].JournalofHydroelectricEngineering,2015,34(1):161-168.
[3] ZHANG Chunze,CHENG Yongguang,WU Jiayang,et al. Lattice boltzmann simulation of the open channel flow connecting two cascaded hydropower stations[J].JournalofHydrodynamicsSer.B,2016,28(3):400-410.
[4] 程永光,杨建东,赖旭,等. 实用水力瞬变过程[M]. 3版.北京:中国水利水电出版社,2015.
CHENG Yongguang, YANG Jiandong, LAI Xu, et al.AppliedHydraulicTransients,ThirdEdition[M]. 3th ed. Beijing:China Water Power Press,2015.
[5] CHENG Yongguang,LI Jinping,YANG Jiandong. Free surface-pressurized flow in ceiling-sloping tailrace tunnel of hydropower plant:Simulation by VOF model[J].JournalofHydraulicResearch,2007,45(1):88-99.
[6] 杨建东,李玲,周俊杰,等. 尾导结合的尾水系统水流中断的机理分析[J]. 水动力学研究与进展A辑,2012,27(4):394-400.
YANG Jiandong,LI Ling,ZHOU Junjie,et al. Study on the water flow disruption in the system of tailrace tunnel combined with diversion tunnel[J].ChineseJournalofHydrodynamics,2012,27(4):394-400.
[7] 朱方磊,程永光. 明渠接竖井水电站引水系统的瞬变流规律[J]. 武汉大学学报(工学版),2015,48(6):744-750.
ZHU Fanglei,CHENG Yongguang. Transient flows in headrace system combining open channel and shaft for hydropower stations[J].EngineeringJournalofWuhanUniversity,2015,48(6):744-750.
[8] HIRT C W,NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J].JournalofComputationalPhysics,1981,39(1):201-225.
1D Shallow Water Wave and 3D VOF Coupling Simulationof Transient Open-Channel Flow
ZHANG Xiaoxi1,ZHANG Chunze2,CHEN Qiuhua3
(1. School of Environmental Science and Engineering,Xiamen University of Technology,Xiamen 361024,Fujian,P. R. China; 2. Chongqing Southwest Scientific Research Institute for Water Transportation Engineering,Chongqing Jiaotong University,Chongqing 400074,P. R. China; 3. School of Civil Engineering and Architecture,Xiamen University of Technology,Xiamen 361024,Fujian,P. R. China)
A numerical method for simulating the transient open-channel flow by coupling 1D shallow water wave and 3D VOF models was proposed. Firstly,by establishing the mathematical relationship between the variables of the two calculation models,the proposed method realized that 3D region provided flow for 1D region and 1D region provided the pressure and volume fraction distribution of water for 3D region. Then,two typical transient conditions of rectangular cross-section channel during load rejection and increase were simulated by coupling method. Comparing the above results with the calculation results obtained by 1D shallow water wave model,it shows that the proposed method is qualitatively correct,and the accuracy is high in quantitative. Finally,the transient open-channel flow in a pressure fore bay of a hydropower station with inlet pipes was simulated by the proposed method,and the critical parameters,such as the maximal overflow discharge,the maximal and minimal water levels were obtained. The coupling method combines the efficiency of 1D model in the calculation of a fine long canal and the accuracy of 3D model in the simulation of local open-channel blast flow,which can provide a better choice for analyzing complex open-channel flow problems in engineering.
hydraulic engineering; transient open-channel flow; numerical simulation; 1D and 3D coupling
10.3969/j.issn.1674-0696.2017.12.10
2016-10-12;
2016-12-02
厦门市科技计划项目(3502Z20150051);厦门理工学院高层次人才项目(YKJ15042R,YKJ14025R);福建省中青年教师教育科研项目(JA15384);重庆市科委自然科学基金计划资助项目(cstc2016jcyjA1935);重庆市教委自然科学基金计划资助项目(KJ1600514)
张晓曦(1986—),男,湖北襄阳人,讲师,博士,主要从事水力学方面的研究。
张春泽(1986—),男,宁夏中卫人,助理研究员,博士,主要从事计算流体力学方面的研究。E-mail: zhangchunze@whu.edu.cn。
TV131.2
A
1674-0696(2017)12-053-05
朱汉容)
