一种改进的桥梁裂缝图像滤波算法*

王 楹

(交通运输部路网监测与应急处置中心，北京 100088)

一种改进的桥梁裂缝图像滤波算法*

王 楹

(交通运输部路网监测与应急处置中心，北京 100088)

针对桥梁裂缝周边复杂的噪声信息，传统的滤波方法在处理此类噪声时虽然能在某方面取得去噪效果，但也往往存在着各自较大的缺陷。对此，在传统的形态学滤波器滤波的基础上，提出了一种基于多角度多结构元素形态学滤波器的算法。通过结合数学形态学，将多种结构元素结合使用，避免了单一结构元素对图像处理时单一的作用，不仅能对图像全区域进行分析，而且保留了图像的细节信息。实验数据对比分析表明，此滤波算法取得了明显的效果。

桥梁工程；形态学；滤波器；桥梁图像；图像去噪

0 引 言

桥梁裂缝在桥梁的建造和使用中都是一种常见病害现象，然而此类病害的相关检测仍旧停滞在人工作业阶段，不仅相关人员的工作强度大、相关检测费用昂贵且检测工作具有一定的危险性[1]。随着近些年来的计算机科学技术发展，基于数字图像技术的桥梁裂缝检测方法越来越受到广泛的应用[2]。对图像部分的处理工作直接影响后期分析结果，因此，对图像的前期处理是数字图像技术的关键。其中，图像去噪效果对图像最后的处理结果显得尤为重要。由于桥梁受自然环境及车辆人员因素的影响，在形成裂缝部分周边有着较为复杂的噪声信息，这对传统的数字图像去噪造成了障碍。传统的均值滤波、中值滤波及形态学滤波器滤波都只能对图像部分噪声具有一定的去噪效果，然并不能很好地解决桥梁裂缝复杂的噪声因素[3]。

针对桥梁裂缝噪声信息来源复杂的现象，在传统的形态学滤波器滤波的基础上，提出一种基于多角度多结构元素形态学滤波器的算法。通过对比传统滤波方法，笔者提出的形态学滤波算法在图像去噪和保留图像细节方面效果显著[4]。

1 图像灰度化

将RGB图像转化为灰色图像的过程称之为图像灰度化。灰色图像与RGB图像相比，灰度值只含有亮度信息而无色彩信息，因此在保持图像色度和亮度等特征不变的情况下，能够显著地减少计算机的运算量，达到简化效果。因此，笔者采用加权平均值法，将3个分量依据其各自的重要性和其他指标以不同的权值加权平均[5]。其转化公式如式(1)：

F(i，j)=0.299R(i，j)+0.587G(i，j)+0.114N(i，j)

(1)

对相应的桥梁裂缝图像进行灰度化处理，结果如图1。

图1 图像灰度化效果Fig.1 Image grayscale effect

2 常见的滤波方法

在将图像进行灰度变换后，与原图像进行对比可以发现，灰度图像中存在细微的像素噪点及周围环境颜色的不协调。此外，桥梁裂缝图像本身在桥梁建造时就因材料或设备的影响而在图像中产生噪声。以上被认为是图像的非本源信息，因此，在进行深入的图像处理前通常会采取一些常见的滤波方法对图像进行去噪处理，通常有如下几种滤波方法。

2.1 均值滤波

均值滤波的原理是采用领域像素模版的像素均值代替目标图像的像素值。通常情况下领域像素模版采用3×3、5×5、7×7这3种尺寸。

采用均值滤波器模版，公式如式(2)：

(2)

笔者采用通常情况下3×3、5×5、7×7这3种大小的模板对桥梁裂缝图像的灰度图像进行均值滤波，仿真结果如图2。

图2 不同模版均值滤波示意Fig.2 Schematic diagram of average filtering of different templates

均值滤波虽然在处理高斯噪声上具有良好的效果，但将其运用在处理桥梁裂缝图像中噪声时却有着十分明显的缺陷，主要表现在将噪声方差缩小若干倍的同时，也把关键信息模型缩小了若干倍。因此它虽然将噪声进行了一定的平滑，却也同时将图像中关键信息模糊了，不能很好地处理桥梁裂缝图像中复杂的噪声信息。

2.2 中值滤波

中值滤波是一种非线性滤波方法，与均值滤波不同的是，中值滤波用排序在中间部分的灰度值来替换相应处理部分的像素值。因此，中值滤波更适用于去除椒盐噪声。

中值滤波处理的原理如图3。

同样采用3×3、5×5、7×7这3种像素尺寸进行中值滤波，仿真结果如图4。

图4 不同模版中值滤波示意Fig.4 Schematic diagram of median filtering of different templates

对比上述图像可看出中值滤波器具有更好的噪声去除效果，同时也很好地保留了桥梁裂缝图中的边缘信息。然而，当我们选取越大的尺寸模版时会发现其丢失的信息也越多，这对桥梁裂缝复杂的图像处理而言是极为不利的，其弊端较为明显。

2.3 形态学滤波器滤波

由数学形态学的基本运算构成的滤波器叫做形态学滤波器。形态学滤波器相对于均值滤波器和中值滤波器的最明显的优点是其选择性地抑制图像的结构，既可以抑制图像中的噪声，也可以抑制图像中与关键信息不相关的图像目标信息[6-7]。

将开启运算和闭合运算进行不同顺序的级联，可以得到两种不同形态的滤波器：开闭滤波器(opening-closing filter)和闭开滤波器(opening-closing filter)[8]。这两种滤波器对于图像中的正负脉冲信号均有着良好的抑制作用。

令f(x)，(x∈zn)表示输入的图像，B表示结构元素，且B⊂Zn那么可以对OC滤波器和CO滤波器作如下定义：

OC[f(x)]=(foB·B)(x)

(3)

CO[f(x)]=(f·BoB)(x)

(4)

形态学滤波器仿真结果如图5。

图5 形态学滤波器示意Fig.5 Schematic diagram of the morphological filter

与线性滤波相比，非线性滤波可以在消除图像中噪声的同时更好地保留图像中的关键信息，因此形态学滤波器在去噪和保留图像关键信息方面具有更好的效果。

3 形态学滤波器的算法的改进

针对桥梁裂缝图像关键信息及噪声信息来源的双重复杂性情况，形态学滤波算法具有更好的处理效果[9-10]。然而，一般情况下形态学滤波只选用一种结构元素对图像进行分析处理，这不仅处理效果单一，更可能会同中值滤波一样对图像细节造成破坏。基于此，笔者结合数学形态学，将多种结构元素结合使用，提出了一种基于多个角度、多种结构元素的形态学滤波算法。

令X表示待处理图像，{Bi}={B1，B2，L，Bn}表示一种有限结构元素序列，X、{Bi}⊂E2或Z2，则对使用多结构元素的膨胀运算和腐蚀运算的定义如下：

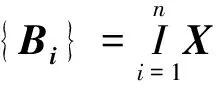
(5)

(6)

对使用多结构元素的开启运算和闭合运算作如下定义：

(7)

(8)

当形态学变换使用多结构元素的时候具有如下特性。

1) 对偶性

X⊕{Bi}=(XcΘ{Bi})c

(9)

XΘ{Bi}=(Xc⊕{Bi})c

(10)

X∘{Bi}=(Xc·{Bi})c

(11)

X·{Bi}=(Xc°{Bi})c

(12)

2) 单调性

X⊆Y⟹X⊕{Bi}⊆Y⊕{Bi}，XΘ{Bi}⊆YΘ{Bi}

(13)

X⊆Y⟹X∘{Bi}⊆Y°{Bi}，X·{Bi}⊆Y·{Bi}

(14)

3) 扩展、收缩性

O∈Bi⟹X⊕{Bi}⊇A，XΘ{Bi}⊆A

(15)

X∘{Bi}⊆XX·{Bi}⊇X

(16)

4) 幂等性

(X∘{Bi})°{Bi}=X∘{Bi}

(17)

(X·{Bi})·{Bi}=X·{Bi}

(18)

5) 如果满足X、{Bi}⊂E2或Z2，同时{Bi}={B1，B2，L，Bn}表示的是一种结构元素序列，而且是有限的，则有如下情况成立：

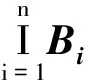
(19)

(20)

6) 如果满足X、{Bi}⊂E2或Z2，同时{Bi}={B1，B2，L，Bn}表示的是一种结构元素序列，而且是有限的，则有如下情况成立：

X∘{Bi}⊇XΘ{Bi}

(21)

X·{Bi}⊆X⊕{Bi}

(22)

当开启运算和闭合运算使用多结构元素的时候，它们的基分解表达式如下：

(23)

(24)

Bij表示{Bi}中的各个子结构元素，其位置由{Bi}的位移决定。假设{Bi}={B1，B2}，则多结构元素的开启运算可表示为：

(25)

根据以上6点特性，通过以下设计得到一种改进的形态学滤波器——多角度多结构元素形态学滤波器。文中的目标滤波器意在获取桥梁裂缝图像中的裂缝信息，过滤与其无关的噪声信息的同时尽量减少对裂缝信息的干扰。考虑到桥梁裂缝图像中裂缝信息一般是线性，因此选用直线元素作为本次实验中的结构元素。选取不同大小的直线元素A、B，角度分别为0、45、90、135。利用不同尺寸在不同角度下的结构元素对待分析图像，先进行形态学开启运算。在开启运算的基础上进行相同尺寸角度的形态学闭合运算[11]。最后将各个尺寸的结构元素在不同角度下的结果图像进行加权计算，获取最终滤波结果图像。根据相关实验数据表明，A、B值大于5时检测裂缝信息会出现丢失，因此A、B的取值暂定为A=1，B=5。

选定4种形状的结构体，根据其形状和模版大小分为4类，分别对对桥梁裂缝图像进行形态学开启和闭合串联滤波。对得到的4张结果图像乘以合适的权数然后进行加权，得到平滑处理的新图像。其中，结构体权数的值由结构体被插入到图像中的次数与总次数的比率确定。

选取直线元素A=1，B=2，4个角度分别选取0、45、90、135，在上述条件下对桥梁裂缝图像进行滤波，再进行加权获得最终滤波结果。滤波效果如图6。

图6 多角度多结构元素形态学滤波器示意Fig.6 Schematic diagram of multi-angle multi-structure element morphology filter

4 实验数据对比与分析

通常情况采用峰值信噪比(peak signal to noise ratio)和均方误差(mean squared error)从客观来评价图像质量好坏。其中，峰值信噪比PSNR的值越大，表示图像失真的越少；均方误差MSE的值越小，表明实验数据越精确。笔者选用的桥梁裂缝图像经过不同滤波方法处理过后的PSNR及MSE值具体如表1。

表1 不同滤波方法的PSNR、MSE值Table 1 PSNR，MSE values of different filtering methods

对表1中的PSNR值及MSE值进行比较可以发现，笔者提出的多角度多结构元素形态学滤波器的PSNR值最大，失真最小，且其MSE值最小，数据最精确。可见，笔者提出的改进的形态学滤波器在PSNR及MSE两个评价指标上明显均优于其他传统滤波器，具有更好的滤波去噪效果。

5 结 语

笔者在传统形态学滤波算法的基础上，根据桥梁裂缝图像中噪声信息的特点，结合数学形态学，将多种结构元素结合使用，提出了一种多角度多结构元素形态学滤波器。仿真实验数据表明，与常用的滤波方法相比较，在同等的技术水平条件下，笔者提出的多角度多结构元素形态学滤波器能够更好地去除桥梁裂缝图像中的噪声而保留有效信息。作为图像预处理环节中的重要一环，去噪的效果将直接影响图像最后的成像，进一步对桥梁裂缝的检测评估工作造成影响。良好的去噪效果可以形成清晰的桥梁裂缝图，因此可以快速高效地检测出桥梁裂缝，及早发现桥梁病害，预防灾难的发生。因此，鉴于笔者提出的多角度多结构元素形态学滤波器在处理桥梁裂缝图像噪声时的独特优势，可以想象，该算法在桥梁检测领域一定有着广阔的应用前景。

[1] 罗忠宝. 在役桥梁裂缝识别分析与防治研究[J]. 武汉理工大学学报，2008，4-35.

LUO Zhongbao. Study on identification and prevention of cracks in existing bridges[J].JournalofWuhanUniversityofTechnology，2008，4 -35.

[2] 许薛军，张肖宁. 基于数字图像的混凝土桥梁裂缝检测技术[J]. 湖南大学学报(自然科学版)，2013，40(7)：34-40.

XU Xuejun，ZHANG Xiaoning. Crack detection technology of concrete bridge based on digital image[J].JournalofHunanUniversity(NaturalSciences)，2013，40(7)：34-40.

[3] IKHLAS A Q，SARA P R，OSAMA A，et al. PCA-Based algorithm for unsupervised bridge crack detection[J].AdvancesinEngineeringSoftware，2006，37(12)：771-778.

[4] 张维峰，刘萌，杨明慧，等. 基于数字图像处理的桥梁裂缝检测技术[J]. 现代交通技术，2008，5(5)：34-36.

ZHANG Weifeng，LIU Meng，YANG Minghui，et al. Bridge crack detection technology based on digital image processing[J].ModernTransportationTechnology，2008，5(5)：34-36.

[5] 付永庆，王咏胜. 一种基于数学形态学的灰度图像边缘检测算法[J]. 哈尔滨工程大学学报，2005，26(5)：685-687.

FU Yongqing，WANG Yongsheng. An edge detection algorithm based on mathematical morphology for gray image[J].JournalofHarbinEngineeringUniversity，2005，26(5)：685-687.

[6] 程军，张桂林. 用于目标检测的灰度形态学滤波器FPGA实现[J]. 计算机工程与设计，2007，28(3)：622-624.

CHENG Jun，ZHANG Guilin. Implementation of Gray-scale morphological filter for target detection[J].ComputerEngineeringandDesign，2007，28 (3)：622-624.

[7] 姜涌，曹杰，谢求成，等. 一种基于形态学梯度矢量和自适应模糊的目标边缘提取算法[J]. 武汉大学学报(信息科学版)，2006，31(6)：484-488.

JIANG Yong，CAO Jie，XIE Qiucheng，et al. An algorithm of object edge extraction based on morphological gradient vector and adaptive[J].JournalofWuhanUniversity(InformationScienceEdition)，2006，31 (6)：484-488.

[8] XU L，LU H. Automatic morphological measurement of the quantum dots based on marker-controlled watershed algorithm[J].IEEETransactionsonNanotechnology，2013，12(1)：51-56.

[9] 张雯，葛玉荣. 基于形态学与不完全树形小波分解的图像纹理特征提取算法[J]. 计算机应用，2011，31(6)：1592-1594.

ZHANG Wen，GE Yurong. An image texture feature extraction algorithm based on morphology and incomplete tree wavelet decomposition[J].JournalofComputerApplications，2011，31 (6)：1592-1594.

[10] 黄豪杰，李榕，常鸿森，等. 基于自适应灰度形态学滤波的车牌图像分割[J]. 微电子学与计算机，2007，24(4)：95-98.

HUANG Haojie，LI Rong，CHANG Hongsen，et al. License plate image segmentation based on adaptive gray morphological filtering[J].MicroelectronicsandComputer，2007，24 (4)：95-98.

[11] 赵春江. 数字图像处理算法典型实例[M]. 北京：人民邮电出版社，2009.

ZHAO Chunjiang.DigitalImageProcessingAlgorithmsTypicalExamples[M]. Beijing：People’s Posts and Telecommunications Press，2009.

An Improved Filtering Algorithm for Bridge Crack Image

WANG Ying

(Ministry of Transport Road Network Monitoring and Emergency Response Center，Beijing 100088，P. R. China)

For the complicated noise information around the bridge crack，the traditional filtering method can get the denoising effect in some aspects when dealing with such noises，but they often have their own big defects. Therefore，based on the traditional morphological filter，an algorithm based on multi-angle multi-structure element morphological filter was proposed. By combining mathematical morphology，a variety of structural elements were combined to avoid the single effect of single structural element on image processing，which could not only analyze the whole region of the image，but also retain the detail information of the image. The comparison analysis on the experimental data shows that the proposed filtering algorithm has achieved remarkable results.

bridge engineering; morphology; filter; bridge image; image denoising

10.3969/j.issn.1674-0696.2017.12.03

2016-11-28；

2017-02-11

国家自然科学基金项目(51479102)

王 楹(1982—)，男，天津人，博士，助理研究员，主要从事路桥研究方面的工作。E-mail：212844665@qq.com。

U447

A

1674-0696(2017)12-013-05

朱汉容)