利用学生函数计算器快速计算缓和曲线的方法

郭有宝

(包头铁道职业技术学院，内蒙古 包头 014060)

利用学生函数计算器快速计算缓和曲线的方法

郭有宝

(包头铁道职业技术学院，内蒙古 包头 014060)

缓和曲线道路中桩坐标计算是学生比较难于学习的知识点，缓和曲线公式多、计算复杂，因此研究缓和曲线很有必要。所以应该研究一个适于学生的算法，本算法抛弃了复杂的坐标平移转换公式，阐述了如何利用普通函数计算器快速计算缓和要素、缓和曲线常数、缓和曲线主点里程及其坐标、缓和曲线逐桩坐标，在日常教学及技能大赛中，得到广泛的应用。

缓和曲线;函数计算器;快速计算;技能大赛

已知起点坐标(XQD,YQD)及里程(KQD)、交点坐标(XJD,YJD)、终点坐标(XZD,YZD)、圆曲线半径(R)、缓和曲线长(l0)，求缓和曲线常数、缓和曲线要素、缓和曲线主点里程及坐标、指定里程的坐标已经成为学习的终点，甚至进入相关技能大赛的科目中。鉴于以上原因，将计算公式优化并结合普通函数计算器的使用，学生可以迅速快捷的将逐桩坐标计算出来，目前在我校教学中得到广泛应用。

为了便于大家学习交流，将该计算的思路与方法整理出来。

缓和曲线示意图如图1所示。

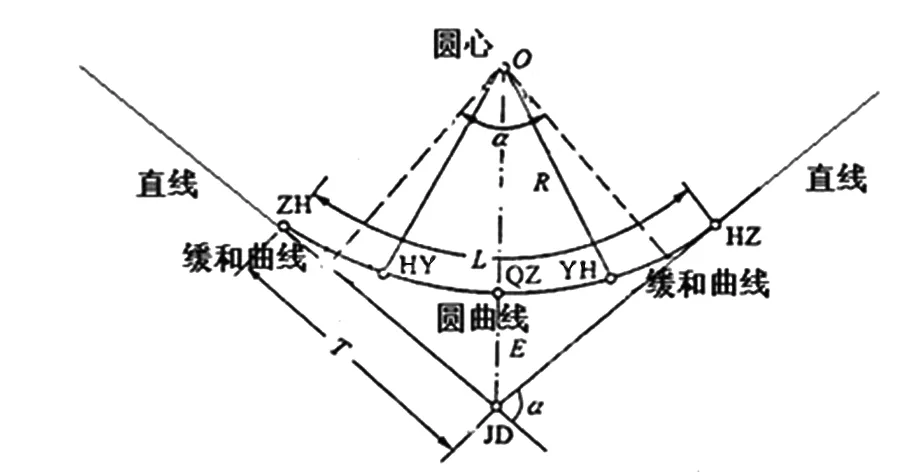
图1 缓和曲线示意图

1 简单介绍计算普通函数计算器的使用过程

以学生正在使用的众成JS-82TL-A计算器为例。

1.1 存储的步骤如下

“STO”+“A”，按键上显示“(-)”，个别计算器需要先使用“SHIFT”键才能激活存储功能。

1.2 调用的步骤如下

“ALPHA”键然后在按“A”键，按键上显示“(-)”，屏幕上显示的内容是“A”。

1.3 坐标正算快捷方法

将边长、方位角变换为坐标增量的方法。

“SHIFT”键+“Pol”键+“ALPHA”键+“A”键+“，”键+“ALPHA”键+“D”键+“)”键+“=”键

坐标增量ΔX，ΔY，分别存储于“E”和“F”中。

1.4 坐标反算快捷方法

将坐标增量变换边长、方位角为的方法。

“Pol”键+“ALPHA”键+“A”键+“，”键+“ALPHA”键+“D”键+“)”键+“=”键

边长D，方位角α，分别存储于“E”和“F”中。

后文公式中出现的A、B、C、D、E、F、X、Y、M分别代表九个独立存储器，分别存储后续步骤相关数据，在使用过程中可能覆盖，一定要按要求存储，否则影响计算结果。

2 缓和曲线计算步骤

2.1 计算缓和曲线常数

Pol(XZD-XJD,YZD-YJD)算出交点和终点方位角α1存储在A中。

Pol(XJD-XQD,YJD-YQD)算出起点和交点方位角α2存储在B中，交点到起点的距离D存储于E中。

调用A-B得到偏角α(若α为正代表右偏，若α为负代表左偏)，记录在草稿纸上并将│α÷2│存储于C上。

β0=90°×l0÷π÷R不需要存储，直接记录在草稿纸上。

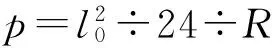
2.2 计算缓和曲线要素

切线长：Th=(R+M)×TanC+D记录并存储于D

曲线长：Lh=π×R×C÷90°+l0记录并存储于F

外矢距：Eh=(R+M)÷CosC-R记录并存储于M

切曲差：Dh=2×D-F记录不用存储

2.3 计算缓和曲线主点里程

缓和曲线主点里程，计算公式如下：

交点里程：KJD=KQD+E

直缓点里程：KZH=KJD-D记录并存储于E

缓圆点里程：KHY=E+l0记录

曲中点里程：KQZ=F÷2+E记录

圆缓点里程：KYH=E+F-l0记录

缓直点里程：KHZ=E+F记录

2.4 计算主点坐标

将交点坐标(XJD,YJD)分别存入X和Y以便后续调用。

REC(D,A)前面的E、F分别被替代

缓直点坐标：XHZ=E+X

YHZ=F+Y记录

REC(M,B±(90°+C))

(注：右偏为正、左偏为负)

曲中点坐标：XQZ=E+X记录

YQZ=F+Y记录

REC(D,B+180°)

直缓点坐标：XZH=E+X记录并存储于X

YZH=F+Y记录并存储于Y

需要先求弦长及弦切角

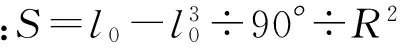
弦切角：θ=30°×l0÷π÷R记录并存储于D

REC(C,(B±D))

(注：右偏为正、左偏为负)

缓圆点坐标：XHY=E+XHZ记录

YHY=F+YHZ记录

REC(C,(A+180°±D))

(注：右偏为负、左偏为正)

圆缓点坐标：XYH=E+XHZ记录

YYH=E+XHZ记录

2.5 计算第一缓和曲线上指定点坐标

P点到直缓点曲线长l

l=KP-KZH,存入A

C=R×l0记录并存储于C

需要先求弦长及弦切角弦长：S=A-A5÷90°÷C2记录并存储于D

弦切角：θ=30°×A2÷π÷C记录并存储于M

REC(D,(B±M))

(注：右偏为正、左偏为负)

P点坐标：Xp=E+X记录

Yp=F+Y记录

2.6 计算缓和曲线中圆曲线上指定点坐标

P点到直缓点曲线长l’

l’=KP-KZH,存入A

β1=180°×A÷π÷R+β0记录并存储于C

XP’=m+R×SinC记录并存储于D

YP’=(R+p)-R×CosC记录并存储于M

pol(D,M)

REC(E,B±F)

(注：右偏为正、左偏为负)

P点坐标：Xp=E+X记录

Yp=F+Y记录

利用高中平面几何学的原理，结合测量学的基本知识用纯数学的公式推导,反复利用快捷的坐标正算坐标反算公式，利用里程差求弦切角及弦长,省略了标准计算方法坐标系统转换的计算办法。此法在学生们的学习中极为便利,能迅速得到缓和曲线上任意点坐标。文中提到的坐标正算的Rec功能、坐标反算的Pol功能以及反复利用9个独立存储及调用相关数据的方法，给学生带来极大的便利。在日常教学中有较好的应用价值，在技能大赛上也有推广。

[1] 郭有宝.利用学生函数计算器的快速计算圆曲线的方法[J].科技视界,2016,(23).

[2] 郭有宝.曲线计算配套验算验算软件开发的一种思路[J].黑龙江交通科技,2017,(2).

[3] 叶礼骞.计算器的使用对中职数学的影响与作用——主要以三角函数为例[J].新课程导学,2011,(31).

U412.6

B

1008-3383(2017)10-0017-02

2017-03-28

郭有宝(1984-)，男，黑龙江人，助教，主要从事测绘工程及高职测量教学工作研究。