小样本下基于竞争失效的轴承可靠性评估

秦荦晟， 陈晓阳， 沈雪瑾

(上海大学 机械自动化工程系,上海 200072)

小样本下基于竞争失效的轴承可靠性评估

秦荦晟， 陈晓阳， 沈雪瑾

(上海大学 机械自动化工程系,上海 200072)

轴承是机械产品中重要的组成部分，其性能和寿命与机械设备的运行寿命密切相关。为获得准确的轴承可靠性评估结果，应当综合考虑不同失效模式对轴承可靠性的影响。针对轴承试验中完全失效的数据，利用Bootstrap法构造轴承寿命分布参数的先验分布，依据Bayes法估计出相应的后验分布，并对后验期望修偏即可获得轴承寿命分布参数。通过进一步分析轴承的振动性能退化数据，获得轴承局部失效的寿命分布。利用Copula函数对轴承的完全失效的寿命分布模型和局部失效寿命模型进行综合分析，借助试验数据点的经验Kendall相关秩估计Copula函数的相关参数，求得轴承竞争失效下的可靠性分析结果，获得的分析结果有助于寻找轴承设计过程中存在的缺陷，提高轴承的可靠度。

轴承；Bootstrap方法；Bayes法；性能退化；Copula函数；可靠性

近年来，轴承产品的使用性能以及轴承的可靠性分析得到了越来越多的关注，如何提高滚动轴承的使用性能、使用寿命，以及如何提高轴承可靠性评估精度成为热点。Dong等[1]基于支持向量机和马尔科夫模型对轴承退化过程做了预测，并通过实例证明了所提出方法的有效性；Edwin等[2]介绍了三种可以通过轴承振动退化数据估计球轴承剩余寿命的方法；Zhang等[3]介绍了如何选取合适的轴承运行参数确定轴承的剩余使用寿命。

基于多种失效模式竞争失效的可靠性分析可以提高轴承可靠性评估的准确性。王华伟等[4]通过构造混合Weibull分布模型对航空发动机的竞争失效进行了分析；唐家银等[5]通过使用Copula函数对多故障模式相关情况下的长寿命产品进行了可靠性分析；常春波等[6]基于系统自然退化过程和冲击过程的分布函数推导出基于竞争失效的系统可靠度函数。Bocchetti等[7]通过假设退化型失效和突发型失效相互独立的情况下，给出了产品在竞争失效下的可靠性。

产品的可靠性试验常常存在样本量少的问题，这会造成对产品可靠性模型参数的估计产生较大误差。可靠性领域中的小样本问题得到了越来越多的重视，蒋喜等[8]应用虚拟样本增广法解决了极小子样下电主轴性能退化的可靠性分析；Xiong 等[9]针对小样本的测试数据提出了一种计算方法，求解产品结构安全的可靠性；Picheny 等[10]通过采用Bootstrap法对有限样本下的试验数据进行分析求得了产品的可靠度。近年来，Bayes方法也被广泛应用于对Weibull分布参数的估计[11-12]。金光[13]提出了一种综合性能与寿命数据的Bayes-Bootstrap法，通过将Bayes方法与Bootstrap方法相结合，计算小样本问题的可靠度。

本文将结合Bootstrap方法以及Bayes分析方法，分析处理轴承试验中的小样本数据，实现小样本试验数据下寿命分布参数的估计；运用Copula函数建立滚动轴承在不同失效模式下竞争失效的可靠性评估模型，并结合Kendall相关秩给出一种Copula函数参数估计的简便方法，实现对竞争失效下滚动轴承的可靠性评估，提高滚动轴承可靠性评估的准确度。

1 机械产品失效模式的分类

Blanche等[14]提出的失效模式分类，指出产品丧失既定功能的失效被称为扩展失效，扩展失效可分为完全失效(Complete Failures)和局部失效(Partial Failures)。完全失效即产品完全丧失既定功能的失效，局部失效即产品丧失部分既定功能的失效。

在机械产品实际使用过程中，机械产品发生的失效可以认为是完全失效和局部失效的竞争失效。

2 多失效模式的轴承可靠性评估模型

2.1 轴承寿命分布模型

由于Weibull分布可以很好地模拟多种分布，因此假设滚动轴承的试验寿命t服从参数为(β,η)的二参数Weibull分布，其中β为Weibull分布的形状参数，η为Weibull分布的尺度参数，Weibull分布的概率密度函数如式(1)所示。

(1)

则产品试验寿命t的分布函数如式(2)所示。

(2)

2.2 完全失效的滚动轴承可靠性评估模型

在小样本情况下，应用Bayes-Bootstrap法来估计Weibull分布参数，求出滚动轴承完全失效下的寿命分布。

2.2.1 Bayes-Bootstrap方法的实现

Bootstrap方法是一种再抽样理论，肖支才等提出了一种非参数的Bootstrap抽样方法，这种抽样方法获得的再生样本点不仅包含原始样本点，还适当地在原始样本点的基础上进行拓展。抽样方法的具体步骤如下：

(1)利用计算机产生[0,1]区间均匀分布的随机数δ;

(2)令θ=(n-1)δ，i=[θ]+1，[·]为向下取正；

(3)令t*=ti+(θ-i+1)(ti+1-ti)；

其中ti是原始样本t1,t2,…,tn按从小到大排序后得到的第i个样本数据，则t*即为所产生的再生样本数据。

重复上述过程B次，就可以获得B组Weibull分布参数β和η的估计值，从而构造β和η的先验概率密度π1(β)和π2(η)。本文假设参数(β,η)是相互独立的，且β和η的先验概率分布均为正态分布，则β和η的联合先验概率密度为

π(β,η)=π1(β)π2(η)

(3)

假设某一产品试验寿命值为t1,t2,…,tn，该产品的试验寿命值服从Weibull分布，则该样品的寿命t1,t2,…,tn在给定参数β和η条件下的极大似然估计可以表示为

(4)

(5)

在β和η的联合先验概率密度为π(β,η)=π1(β)π2(η)的情况下，根据Bayes公式，有

f(β,η|t1,t2,…tn)=

(6)

式(6)中，Θ表示(β,η)的取值空间。由式(3)、式(6)可知，Weibull分布参数β和η的后验概率密度分别为

(7)

(8)

式(7)、(8)中，Θ1表示β的取值空间，Θ2表示η的取值空间。由于式(7)、(8)中的积分不容易求解，因此参数β和η的后验分布很难得到具体的形式，可以用β和η的后验期望作为β和η的Bayes点估计值。由(7)、(8)可以得到β和η的Bayes点估计值:

(9)

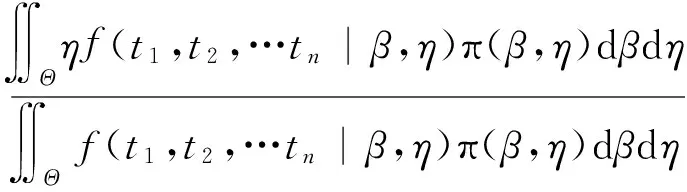
(10)

在可靠性试验的评估结果中，β和η的值分别存在一定有界的范围[β1,β2]和[η1,η2]，使得式(11)和式(12)成立。

(11)

(12)

这样式(9)、(10)可以被进一步改写成式(13)、(14)的形式。

(13)

(14)

对式(13)、(14)作有限范围内的数值积分，求出β和η后验分布的期望值作为Weibull分布参数的估计值。

(15)

(16)

2.2.2 模型的验证

利用计算机随机生成5个服从分布参数已知的Weibull分布随机数，运用2.2.1提出的方法分别估计5个随机数的Weibull分布参数。针对不同的分布参数分别进行试验，获得的结果如表1所示。

表1Weibull分布参数估计结果对比

Tab.1ThecomparisonoftheWeibulldistributionparametersestimatedbydifferentmethods

真实值(β,η)极大似然估计值(β,η)2.2.1方法计算结果(β,η)(1.5,1500)(1.08,1196.08)(1.25,1343.6)(1.8,1800)(1.49,1248.83)(1.75,1467.73)(2,1600)(1.42,1083.27)(1.6,1282.31)(2.5,2000)(1.79,1745.78)(1.94,1923.36)(2.5,2200)(2.07,1690.88)(2.31,1937.76)(3,2000)(2.49,1606.1)(3.00,1939.39)

由表1的计算结果可知在样本量较小的情况下，2.2.1的方法求得的结果更准确。

2.3 局部失效的滚动轴承可靠性评估模型

轴承的局部失效寿命数据可以通过追踪其性能参数获得。基于性能退化的产品可靠性评估目前已有多种较为成熟的计算模型[17-18]，对于滚动轴承产品，也可以选取其性能指标，考虑采用拟合退化轨迹的方法估计出滚动轴承达到失效阈值所需要的时间，如图1所示。

图1 性能退化轨迹图Fig.1 The figure of the performance degradation trace

通过退化轨迹所求得的轴承达到失效阈值的时间即轴承的失效时间，由此运用2.2提出的计算方法即可计算轴承的性能退化寿命分布。

2.4 竞争失效的滚动轴承可靠性评估模型

针对多失效模式竞争可靠性分析，运用Copula函数分析求解基于多失效模式滚动轴承可靠度评估模型。

由Sklar定理[19]可知，联合概率密度f(x,y)可以表示为式(17)的形式：

f(x,y)=c(F(x),G(y))f(x)g(y)

(17)

式中，c(F(x)和G(y))表示相应的Copula密度函数，f(x)和g(y)分别为F(x)、G(y)的概率密度函数。

在常见的Copula函数形式中，Gumbel Copula函数结构与Lee[20]提出的一类二元Weibull分布的生存函数结构相似，因此选用Gumbel Copula对轴承进行竞争失效分析。令F(x)=u，G(y)=v，则Gumbel Copula的函数结构如式(18)所示。

θ∈(0,1]

(18)

对Copula函数的参数估计有多种估计方法，但计算过程复杂，不便于工程应用。然而利用试验数据点的经验Kendall相关秩估计Copula函数的相关参数，可以简化计算，便于工程应用。

Kendall相关秩被描述为任意两对数据和谐的概率与不和谐的概率之差[19]。如果用τ表示Kendall相关秩，假设数据组{(x1,y1),(x2,y2),…(xn,yn)}是连续随机变量向量(X,Y)的n个随机观测值，如果(xi-xj)(yi-yj)>0，则称数据对(xi,yi)与数据对(xj,yj)是和谐的；如果(xi-xj)(yi-yj)<0,则称(xi,yi)与(xj,yj)是不和谐的，用P[(xi-xj)(yi-yj)>0]表示两个数据对和谐的概率，P[(xi-xj)(yi-yj)<0]表示两个数据对不和谐的概率，则Kendall相关秩τ可以表示为

(19)

由文献[21]可知，Gumbel Copula函数的参数θ与其相应的Kendall相关秩τ存在如下关系：

τ=1-θ

(20)

因此，可以将试验数据点的经验Kendall相关秩看作Gumbel Copula函数的Kendall相关秩τ，这样就可以快速而又简便的估计出Gumbel Copula函数参数θ的值。

3 实例分析

针对某型号滚动轴承进行4 000 h的定时截尾寿命试验。试验采用CGS3-8型高温高速微型轴承试验机，试验转速58 000 r/min，轴向载荷5 N。在试验的过程中测量轴承的振动加速度值，根据客户的要求，试验轴承的振动加速度值超过1.5 g时，就认定轴承已失效，并停止试验。试验中投入了7套轴承，共失效5套，轴承的寿命数据如表2所示，其中样品1和样品2均因为振动加速度值超过阈限停止试验，样品6、样品7均未发生失效，所注寿命时间为截尾时间。

表2 轴承试验数据Tab.2 Test data of the ball bearings

为预测样品3、样品4、样品5、样品6、样品7的局部失效发生时间，截取这5套轴承失效前600 h的振动数据，如图2、图3、图4所示；截取样品6和样品7截尾时间前600 h的振动数据，如图5、图6所示。

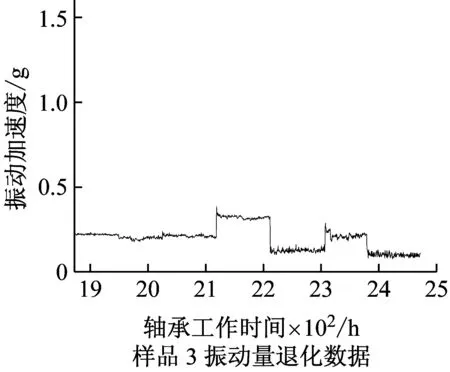
图2 样品3振动退化数据Fig.2 The vibration data of Sample 3

图3 样品4振动退化数据Fig.3 The vibration data of Sample 4

图4 样品5振动退化数据Fig.4 The vibration data of Sample 5

图5 样品6振动退化数据Fig.5 The vibration data of Sample 6

图6 样品7振动退化数据Fig.6 The vibration data of Sample 7

依据文中局部失效和完全失效的定义可判定样品1和样品2失效类型为局部失效，而样品3、样品4、样品5在发生失效时振动未超过阈值，因此可判定样品3、样品4、样品5的失效类型是完全失效。

3.1 轴承完全失效的寿命分布计算

由试验数据可知样品3、样品4、样品5为完全失效，失效时间分别为2 472 h、2 506 h、3 382 h，而样品1在1 313 h未发生完全失效，样品2在2 288 h未发生完全失效，样品6和样品7在4 000 h均未发生失效。结合数据类型，可将滚动轴承完全失效的寿命数据看作随机截尾试验，由参考文献[22]可知，寿命分布参数β和η可通过求解方程(21)获得。

(21)

式中:β和η分别是Weibull分布的形状参数和尺度参数;ti是失效数据;则λi=1；如果ti是截尾数据，则λi=0。

结合参考文献[23]对小样本下定时截尾试验寿命数据的处理方法，应用Bootstrap方法重复抽样5 000次。再利用2.2中的寿命分布参数估计方法对Weibull分布参数进行估计，得到轴承完全失效的寿命曲线如图7所示。

图7 轴承完全失效寿命分布曲线

Fig.7 Life distribution curve of bearings under complete failure

3.2 轴承局部失效的寿命分布计算

这里选用指数形式的退化轨迹y=a·exp(bt)来拟合轴承的振动数据。计算所得轴承振动值达到失效阈值的时间即轴承的局部失效寿命时间，如表3所示，并采用2.2.1提出的方法进行计算，得到轴承局部失效的寿命曲线如图8所示。

表3 轴承局部失效的寿命数据Tab.3 Lifetime data of the ball bearings under partial failure

图8 轴承局部失效寿命曲线Fig.8 Life distribution curve of bearings under partial failure

3.3 竞争失效下轴承可靠性评估

4 结果与讨论

4.1 基于竞争失效评估结果的比较

文中2.3提出的模型充分考虑了不同失效模式之间的相关性，不同失效模式竞争下的轴承可靠度计算结果如表4和图10所示。

图9 竞争失效的轴承可靠性曲线

Fig.9 Reliability curve of bearings under competing failure modes

从图10中可以看出不考虑失效模式之间的相关性会使得可靠性的评估结果偏低，结合可靠性试验，该型号7套轴承在试验前1 300 h没有发生失效，由表4的计算结果可知利用Copula函数求得的可靠性评估结果更符合试验情况。

4.2 轴承可靠性评估结果的分析

图11截取了前1 500 h完全失效与局部失效的概率进行对比，发现在轴承运转的过程中完全失效与局部失效都有存在。在1 100 h之前，轴承发生局部失效的可能性相对较大，而在1 100 h之后，轴承发生完全失效的可能性相对较大。由此可知，在轴承运行的早期，轴承更容易发生局部失效，需要进一步寻找引起失效的原因，提高轴承的早期的可靠度；在1 100 h后，轴承的失效率主要由完全失效引起的，需要进一步寻找轴承完全失效的具体原因，以提高轴承整体的可靠度。

表4 可靠度计算结果对比Tab.4 The comparison of the reliability assessment

图10 不同计算方法的可靠性结果Fig.10 Reliability assessment result calculated by different ways

图11 完全失效与局部失效失效率对比

Fig.11 The comparison of the failure rate under complete failure and partial failure

5 结 论

(1) 轴承的失效是多种失效模式竞争失效的结果，在对轴承的可靠性评估中需要考虑多种失效模式对轴承可靠度的影响以及不同失效模式之间的相关性。

(2) 针对小样本试验数据，运用Bootstrap方法构造试验样本的先验信息，采用Bayes的方法估计出相应的后验结果，并与原始试验数据的计算结果融合，获得小样本下分布参数的估计结果。

(3) 应用Gumbel Copula函数模型，实现对滚动轴承竞争失效可靠度的评估。通过试验数据点的经验Kendall相关秩估计Copula函数的相关参数，计算过程简便，易于工程应用。

(4) 通过对滚动轴承实例的分析，发现如果不考虑失效模式之间的相关性可能会低估轴承运转的可靠性。

(5) 对滚动轴承竞争失效下的可靠性分析有助于提高滚动轴承可靠性评估的准确度，为制定提高轴承可靠性的相关决策提供依据。

[1] DONG S J, YIN S R, TANG B P, et al. Bearing degradation process prediction based on the support vector machine and Markov model[J]. Shock and Vibration, 2014(1): 1-15.

[2] SUTRISNO E, OH H, VASAN A S S, et al. Estimation of remaining useful life of ball bearings using data driven methodologies[C]. IEEE Conference on Prognostics & Health Management, 2012: 1-7.

[3] ZHANG B, ZHANG L J, XU J W. Degradation feature selection for remaining useful life prediction of rolling element bearings[J]. Quality and Reliability Engineering International, 2016, 32(3): 547-554.

[4] 王华伟，高军，吴海桥. 基于竞争失效的航空发动机剩余寿命预测[J].机械工程学报，2014，50(6): 197-205.

WANG Huawei, GAO Jun, WU Haiqiao. Residual remaining life prediction based on competing failures for aircraft engines[J]. Journal of Mechanical Engineering, 2014, 50(6): 197-205.

[5] 唐家银，何平，梁红琴，等. 多故障模式高长寿命产品相关性失效的综合可靠性评估[J].机械工程学报，2013，49(12): 176-182.

TANG Jiayin, HE Ping, LIANG Hongqin, et al. Comprehensive reliability assessment of long-life products with correlated multiple failure modes[J]. Journal of Mechanical Engineering, 2013, 49(12): 176-182.

[6] 常春波，曾建潮.δ冲击条件下相关性竞争失效过程的系统可靠性建模[J]. 振动与冲击，2015，34(8): 203-208.

CHANG Chunbo, ZENG Jianchao. Reliability modeling for dependent competing failure processes underδ-shock[J]. Journal of Vibration and Shock, 2015, 34(8): 203-208.

[7] BOCCHETTI D, GIORGIO M, GUIDA M, et al. A competing risk model for the reliability of cylinder liners in marine Diesel engines[J]. Reliability Engineering and System Safety, 2009, 94(8): 1299-1307.

[8] 蒋喜，刘宏昭，刘丽兰，等. 基于伪寿命分布的电主轴极小子样可靠性研究[J]. 振动与冲击，2013，32(19): 80-85.

JIANG Xi, LIU Hongzhao, LIU Lilan, et al. Extremely small-scale sample’s reliability of an electric spindle based on distribution of false lifetime[J]. Journal of Vibration and Shock, 2013, 32(19): 80-85.

[9] XIONG J, SHENOI R A, GAO Z. Small sample theory for reliability design[J]. The Journal of Strain Analysis for Engineering Design, 2002, 37(1): 87-92.

[10] PICHENY V, KIM N H, HAFTKA R T. Application of the bootstrap method in conservative estimation of reliability with limited samples[J]. Structural & Multidisciplinary Optimization, 2010, 41(2): 205-217.

[11] KURZ D, LEWITSCHNIG H, PILZ J. Advanced Bayesian estimation of Weibull early life failure distributions[J]. Quality and Reliability Engineering International, 2014, 30(3): 363-373.

[12] ERTO P. New practical bayes estimators for the 2-parameter Weibull distribution[J]. IEEE Transactions on Reliability, 1982, 31(2): 194-197.

[13] 金光. 一种综合性能与寿命试验数据的Bayes-Bootstrap方法[J]. 宇航学报，2007，28(3): 731-734.

JIN Guang. A Bayes-Bootstrap method synthesizing performance and life data[J]. Journal of Astronautics, 2007, 28(3): 731-734.

[14] RAUSAND M. 系统可靠性理论：模型、统计方法及应用[M].郭强，王秋芳，刘树林译. 2版.北京：国防工业出版社，2011.

[15] 肖支才，高华明，丁通，等. 自助法在小样本数据均值估计中的应用[J].海军航空工程学院学报，2009，24(5): 563-572.

XIAO Zhicai, GAO Huaming, DING Tong, et al. Research on data anlysis of small sample based on bootstrap method[J]. Journal of Naval Aeronautical and Astronautical University, 2009, 24(5): 563-572.

[16] EFRON B, TIBSHIRANI R. An introduction to the Bootstrap[M]. New York: Chapman hall, 1993.

[17] LU C J, MEEKER W Q. Using degradation measures to estimation time-to-failure distribution[J]. Technometrics, 1993, 35(2): 161-174.

[18] 赵建印，刘芳，孙权，等. 基于性能退化数据的金属化膜电容器可靠性评估[J]. 电子学报，2005，33(2): 378-381.

ZHAO Jianyin, LIU Fang, SUN Quan, et al. Reliability estimate of metallized-film pulse capacitor from degradation data[J]. Acta Electronica Sinca, 2005, 33(2): 378-381.

[19] NELSEN R B. An introduction to Copulas. (Second Edition)[M]. Springer, 2005.

[20] LEE L. Multivariate distributions having Weibull properties[J].Journal of Multivariate Analysis, 1979, 9(2):267-277.

[21] 唐家银，何平，陈崇双. 相关性失效机械系统的可靠性分析方法[M].北京：国防工业出版社，2014.

[22] 陈家鼎. 随机截尾情形下Weibull分布参数的最大似然估计的相合性[J]. 应用概率统计，1989，5(3): 226-223.

CHEN Jiading. On the consistency of maximum likelihood estimators based on randomly censored data in the Weibull distribution case[J]. Chinese Journal of Applied Probability and Statistics, 1989, 5(3): 226-223.

[23] 夏新涛，章宝明，徐永智. 滚动轴承性能与可靠性乏信息变异过程评估[M].北京：科学出版社，2013.

Reliabilityassessmentofbearingsbasedoncompetingfailureundersmallsampledata

QIN Luosheng, CHEN Xiaoyang, SHEN Xuejin

(Department of Mechanical Automation Engineering, Shanghai University, Shanghai 200072, China)

Bearings are important parts in machinery products. Their performance and life are closely related to operating lives of mechanical systems. It is necessary to consider the effects of different failure modes on rolling bearings’ reliability. Here, aiming at the full failure data in bearings’ reliability tests, the prior distributions of bearing life distribution parameters were established with Bootstrap method. Then, the corresponding posterior distributions were estimated using Bayes method. The bearing life distribution parameters were obtained through the posterior expectation reduction. The life distribution model of bearing local failure was gained through further analyzing bearings’ vibration performance degradation data. Copula function was used to analyze comprehensively the life distribution model of bearing full failure and that of bearing local failure. The relative parameters of Copula function were estimated with the experience Kendall relative ranks of test data. Finally, the reliability assessment results of bearings under competing failure were achieved. The results were helpful to find defects in bearing design and improve the bearing reliability.

bearings; Bootstrap method;Bayes method; performance degradation; Copula function; reliability

国家“十二五”规划项目(D.50-0109-15-001,D.71-0109-14-197)

2016-05-30 修改稿收到日期：2016-09-12

秦荦晟 男，硕士生,1992年生

沈雪瑾 女,博士,教授,1963年生

TH133.33;TB114.3

A

10.13465/j.cnki.jvs.2017.23.036