解直角三角形的应用

文 /陈德前

解直角三角形的应用

文 /陈德前

解直角三角形的应用是中考命题的热点素材.解决这类问题的基本思路是从具体情境中抽象出数学问题，建立数学模型并求出结果.下面以2017年中考题为例，对解直角三角形的题型进行归类，供你学习时参考.

一、仰角与俯角问题

例1如图1所示，一架水平飞行的无人机AB，在尾端点A测得正前方桥的左端点P的俯角为α，其中无人机的飞行高度AH为米，桥的长度为1255米．

（1）求点H到桥左端点P的距离；

（2）若在无人机前端点B测得桥的右端点Q的俯角为30°，求这架无人机的长度AB．

解：（1）在Rt△AHP中，

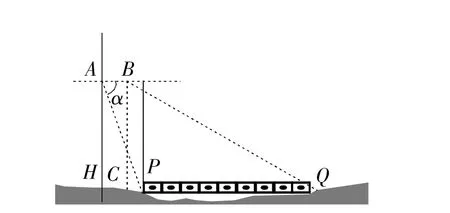
图1

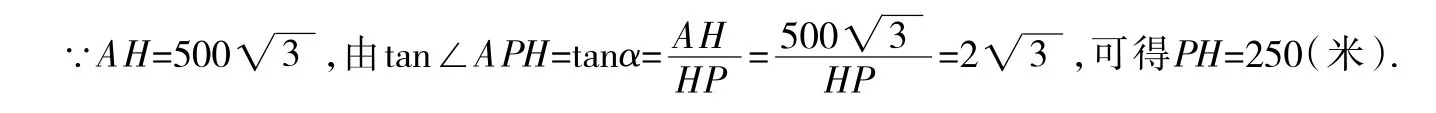
答：点H到桥左端点P的距离为250米.

（2）作BC⊥HQ于点C．在Rt△BCQ中，

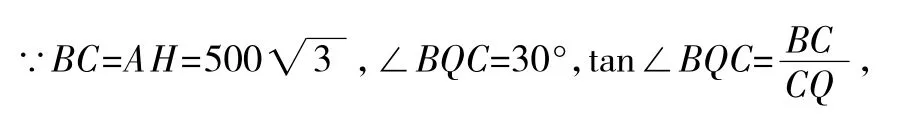
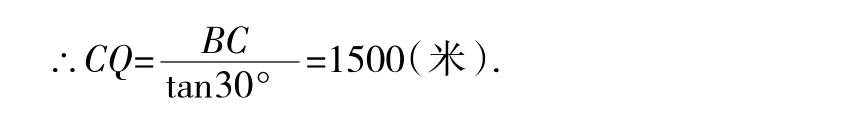
∵PQ=1255米，∴CP=CQ-PQ=245米.

∵HP=250米，∴AB=HC=HP-PC=250-245=5（米）．

答：这架无人机的长度AB为5米．

方法归纳：这类问题通常涉及到多个仰角与俯角.要准确理解仰角、俯角的概念，在已知仰角与俯角的直角三角形中求出相关线段的长度，利用线段解决问题.

二、方位角问题

例2一艘渔船位于港口A北偏东60°方向，距离港口20海里的B处，它沿北偏西37°方向航行至C处突然出现故障，在C处等待救援.B，C之间的距离为10海里，救援艇从港口A出发20分钟到达C处，求救援艇的航行速度.（sin37°≈0.6，cos37°≈0.8，，结果取整数）

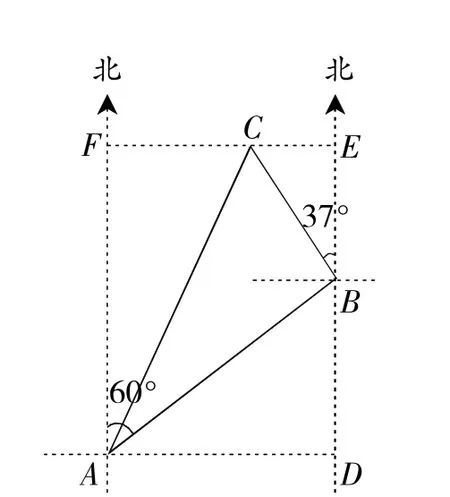
图2

解：如图2所示，作BD⊥AD，BE⊥CE，CF⊥AF.

由题意可知，∠FAB=60°，∠CBE=37°，∴∠BAD=30°.

∵AB=20海里，∴BD=10海里.

在Rt△BCE中，CE=BC·sin37°≈0.6×10=6（海里），

EB=BC·cos37°≈0.8×10=8（海里）.

易知四边形ADEF是矩形，

∴EF=AD=17.32海里，

∴FC=EF-CE=11.32（海里），AF=ED=EB+BD=18（海里）.

答：救援艇的航行速度是64海里/时．

方法归纳：添加辅助线构造直角三角形是解题的关键.构造不同的直角三角形，解题过程有简繁之分，注意从不同的解法中选取最佳解法.

三、坡度、坡角问题

例3为做好防汛工作，防汛指挥部决定对某水库的水坝进行加高加固.专家提供的方案是：水坝加高2米（即CD=2米），背水坡DE的坡度i=1∶1（即DB∶EB=1∶1），如图 3所 示，已知 AE=4米，∠EAC=130°.求水坝原来的高度BC．（参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.2）

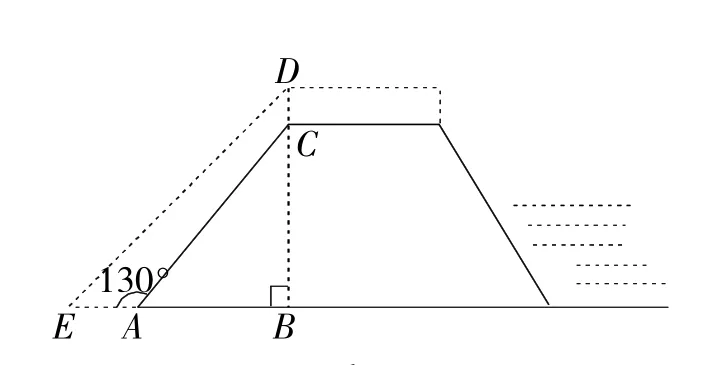
图3

解：设BC=x米.

在Rt△EBD中，∵i=DB∶EB=1∶1，∴BD=BE，

答：水坝原来的高度为12米．

方法归纳：将坡度、坡比转化为线段的比，构造直角三角形求解.当关系比较复杂时，可设未知数，用未知数表示不同的量，列方程求解．

四、其他问题

例4图4是太阳能热水器装置的示意图，利用玻璃吸热管可以把太阳能转化为热能，玻璃吸热管与太阳光线垂直时，吸收太阳能的效果最好.假设某用户要求根据本地区冬至正午时刻太阳光线与地面水平线的夹角（θ）确定玻璃吸热管的倾斜角（太阳光线与玻璃吸热管垂直），请完成以下计算：如图5，AB⊥BC，垂足为点B，EA⊥AB，垂足为点A，CD∥AB，CD=10cm，DE=120cm，FG⊥DE，垂足为点G.

（1）若∠θ=37°50′，则AB的长约为_______cm；

（2）若FG=30cm，∠θ=60°，求CF的长．

（参考数据：sin37°50′≈0.61，cos37°50′≈0.79，tan37°50′≈0.78）

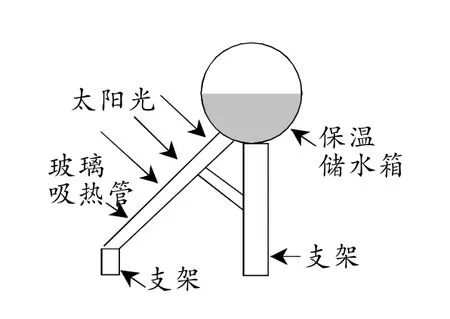
图4

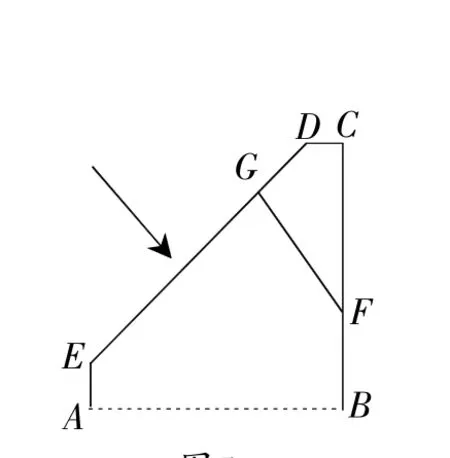
图5

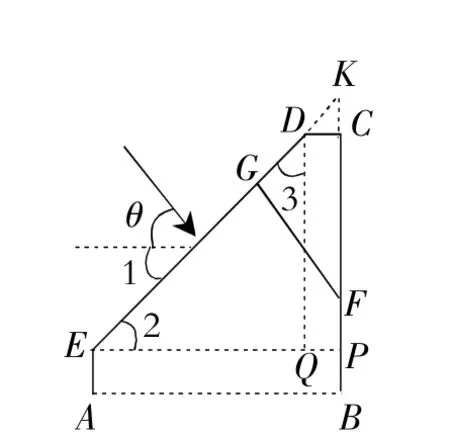
图6

解：（1）如图6，作EP⊥BC于点P，作DQ⊥EP于点Q，则CD=PQ=10，∠2+∠3=90°.

∵∠1+∠θ=90°，且∠1=∠2，∴∠3=∠θ=37°50′，则EQ=DE·sin∠3=120×sin37°50′，

∴AB=EP=EQ+PQ=120sin37°50′+10=83.2（cm）.

（2）如图6，延长ED、BC交于点K，由（1）知∠θ=∠3=∠K=60°.

方法归纳：将实物（或剖面图）转化为数学图形求解.

王二喜