初中数学体验式活动课的教学实践与思考

■钱德春 顾长亮

初中数学体验式活动课的教学实践与思考

■钱德春 顾长亮

“初中数学体验式活动课”是指学生在教师的引导下，从问题（或问题情境）出发，经历和参与操作、观察、发现、抽象、验证、运用的初中数学探究活动课，具有问题性、参与性、过程性、开放性、结构性等特点，通过“操作探究”、“实验验证”、“拓展应用”等方式，让学生建构数学知识，提高创新能力，形成理性精神，积累活动经验。

初中数学 体验式 活动课 操作探究 实验验证 拓展应用

《义务教育数学课程标准（2011年版）》（以下简称《课标2011年版》）指出：“数学活动经验的积累是提高学生数学素养的重要标志。”而经验积累的载体是数学活动，离不开学生的参与与体验。那么，什么是体验式数学活动？体验式数学活动对学生的数学学习有何意义？初中数学体验式活动课有何特点？初中数学体验式活动课的模式是什么？本文结合泰州市十二五规划课题“初中数学活动课程体验教学模式实践研究”的研究，谈谈相关问题的实践与思考。

一、体验式数学活动对学生发展的意义

1.体验式数学活动可以有效建构数学知识。

数学基础知识、基本技能和基本思想方法是数学教学的重要目标，数学活动的核心是“问题解决”，因此体验式数学活动可以引导学生在探究与解决问题中建构知识、增强技能、感悟思想。

2.体验式数学活动可以提高学生创新能力。

《课标2011年版》在实验稿基础上增加了“发现问题、提出问题”的能力要求，这是提出了培养学生创新的能力要求。而数学活动是学生“经历参与操作、观察、发现、抽象、验证、运用、迁移”的过程，其中，“观察、发现、抽象”的过程正是培养学生创新能力的载体。

3.体验式数学活动可以培养学生理性精神。

发现与抽象的数学结论是否正确、有何价值，这就需要“验证、运用与迁移”。要帮助学生经历证实（或证伪）的推理过程，养成言而有据、思辨有理的理性精神与思维习惯。

4.体验式数学活动可以积累数学活动经验。

辩证唯物主义认为，经验是在社会实践中产生的，它是客观事物在人们头脑中的反映。而数学活动经验是学生经历数学活动后在大脑中的积淀，既包括学生经历数学活动获得的直接经验，也包括学生自我反省提炼出来的间接经验，学生的基本活动经验经过积淀与升华，还可以形成数学的直观能力。而无论是何种经验，都建立在学生对活动过程的经历、参与和体验的基础之上。

二、初中数学体验式活动课的特点

初中数学体验式活动课有五大特点，即问题性、参与性、过程性、开放性和结构性。

1.问题性。数学活动过程是发现、提出、分析和解决问题的过程。好的数学活动课首先必须有好的问题，一方面体现活动的价值，学生才有参与探究的欲望；另一方面培养学生用数学的眼光观察现实世界的习惯。

2.参与性。这是数学活动最根本的要求。学生只有亲身参与，才能增强对活动的深切体验；学生只有深度参与，才能将数学活动经验升华为数学知识、思想和方法；学生只有全程参与，才能感悟数学探究“问题情境的数学化、问题猜想的验证、数学结论的应用”全过程，进而内化为自身的研究思路、解决策略与思维方式。

3.过程性。《课标2011年版》指出：“教学活动是师生积极参与、交往互动、共同发展的过程。课程内容的组织要重视过程，处理好过程与结果的关系。”初中数学体验式活动课则对引导学生经历活动过程提出了更高的要求。要全景呈现数学结论的探究与发现过程，全面暴露数学知识的发生与发展过程，全程展示数学思想方法的形成过程。

4.开放性。一是问题的开放。问题开放，既能让学生在交流中获得共同成长，又能让不同的学生有不同的发展。二是过程的开放。既要注意课堂生成性，视活动情况及时调整方向，又要提倡活动多样性，做到教师引导与学生活动、自主探究与合作交流、操作猜想与结论实证的有机融合。

5.结构性。一是课堂活动具有一定的程序结构。一般为“操作、观察、发现、猜想、抽象、验证、运用、迁移、反思”，当然活动环节可视具体要求适当增减；二是学生之间具有一定组织形式，比如在探索活动前将学生分组并分工，明确组长、汇报者、操作者、记录者等。

三、初中数学体验式活动课模式解析

1.模式简介。

根据不同的活动目标与学习内容，初中数学体验式活动课大致分为“操作探究”“实验验证”“拓展应用”三种模式。

一是“操作探究”型活动课模式。以“实验操作，发现结论；启发引导，证明结论；规范表征，应用结论”为主线。学生通过操作、观察、发现，提出结论，在教师引导下对结论进行证明（证实或证伪），并对具有一般意义的结论在应用中巩固与内化。这是从具体到抽象的活动方式，适用于对数学新知的学习，有利于培养学生思辨精神与思维习惯。

二是“实验验证”型活动课模式。以“数学推理，证明结论；操作实验，验证结论；实践应用，深化结论”为主线。这是从抽象到具体的数学活动方式，适合对从数学内部提出并证明的结论，再通过实物模型、现实情境或现场演示加以说明或验证，将抽象的数学概念或结论具体化、形象化、可视化，有利于学生理解。

三是“拓展应用”型活动课模式。以“回顾温习，激活结论；方案设计，应用结论；交流比较，内化结论”为主线。是在学生已有知识和经验的基础上，设计更高层次的方案或情境，从而达到数学结论的升华、迁移与反思的效果。这是从抽象到具体再到抽象的数学活动方式，适用于章节或单元内容学习结束后知识、方法的提炼与小结阶段。

2.案例选析。

这里以“拓展应用”型活动课为例，谈谈模式在数学教学中的具体应用。这是苏科版八年级下册“8.3频率与概率”学习结束后安排的一节活动课。学生已认识“确定事件”与“随机事件”，知道了“事件可能性”的大小和“概率”的概念，掌握了用频率估计概率的方法。本活动旨在通过活动激活“频率与概率及其关系”等相关知识，以此设计更高层次的活动，强化知识的应用，理解随机与统计意识融合的理念，从而加深对频率与概率关系的理解。

环节一：回顾温习，激活结论。

问题1 频率与概率有何关系？

问题2 在如图1所示的图形中随机撒一把豆子，计算落在A、B、C三个区域中豆子数的比。多次重复这个试验，你能否发现上述比值与A、B、C三个区域的面积有何关系？

【操作与思考】学生观察思考，记录试验结果，然后分组试验。每组试验20次，并统计各组的试验数据，并思考：

（1）对照试验的结果，落在A、B、C三个区域中豆子数的比是否具有一定的稳定性？

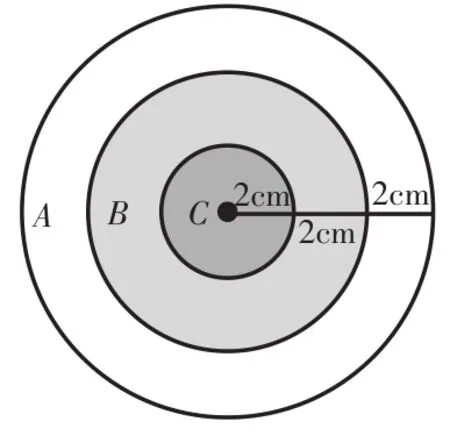
图1

（2）上述比值与A、B、C三个区域的面积有何关系？

（3）这表明落在A、B、C三个区域中豆子数的多少与什么有关？

问题3如果将“豆子落在区域C”记作事件W，请估计事件W发生的概率。

经过思考得出：根据频率估计概率，落在区域C中的豆子数与落在A、B、C三个区域中豆子总数之比，可以作为“豆子落在区域C”的概率。

【设计意图】教师直接提出问题，学生回顾相关知识、方法内容，并通过动手试验，收集、整理、分析实验数据，用频率估计几何概型试验中的概率，从而激活学生对频率与概率关系的认识。

环节二：方案设计，应用结论。

问题4“现有3张扑克牌，其中只有1张黑桃，3个同学依次抽取。”根据这一情境，请设计一个用频率估计概率的问题，写出设计方案，并具体实施，作出数据分析与判断。

【设计与应用】（1）学生尝试用列举法比较困难，选择用频率估计概率；（2）学生分组试验，记录试验次数、每次试验抽中黑桃的人数；（3）每组试验20次，计算20次试验中每个人抽中黑桃的次数并计算频率，将全班同学试验数据汇总；（4）统计随着试验次数增加时每个人抽中黑桃的频率；（5）活动结论：一是随着试验次数增加，频率稳定在左右；二是抽到黑桃的概率跟抽取的顺序无关。反思实验活动过程并思考：（1）上述两个试验的概率是通过怎样的方法得到的？（2）你觉得试验在求概率中有何作用？（3）你觉得概率在生活中对你有何帮助？

【设计意图】教师提出开放性问题，引导学生设计解决问题方案，学生经过试验、筛选，确定合理的用频率估计概率的方案。经历这个过程，学生感受到在大量重复试验中，随着试验次数的增加，频率趋于稳定，从而体会到数学方法可以解释生活中很多现象的原因，试验在求概率中的作用及概率在生活实际中的作用。

环节三：交流比较，内化结论。

【交流与讨论】（1）就“抓阄公平吗？”采访一下自己的父母或朋友，用你所学的数学知识和他们进行交流；（2）如图 2，在正方形ABCD中随机选取一点，你能设计一个试验，并用频率估计概率的方法求出此点恰在△ABO内部的概率吗？

【设计意图】引导学生交流讨论：各组设计的活动方案的正确性、合理性、公平性，从而进一步深化对频率与概率之间的关系的理解。

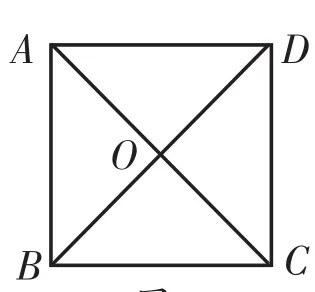
图2

四、初中数学体验式活动课的思考

1.成效显著提升。

经过几年的实践，模式的探究取得了一些成效。从学的角度看，学生增强了数学学习的兴趣，逐步养成了操作、观察、猜想、推理、应用的问题探究的学习习惯，形成了“具体——抽象——具体——更高级抽象”和“质疑——证明（证实或证伪）”的思维方式，培养了追求真理的数学理性精神。从教的角度看，数学课堂由“灌输式变成活动式”，教学方式由“讲授式变成探究式”，知识教学由“数学到数学变为由情境到数学”。

2.问题不可回避。

一是部分教师为活动而活动，丧失了活动的数学教育功能。初中数学体验式活动课是以活动为载体的，在活动中感悟与感受，最终指向数学思维与创新能力的发展；二是并非所有教学内容都适合数学活动，其标准如何界定？三是数学活动与应试升学的关系如何处理？客观地说，开展初中数学体验式活动课费时费脑，短时间内可能对考试成绩有一定的负面影响。针对目前的评价机制，如何引导教师改变短视行为，真正上好数学体验式活动课，有待于从评价体系上加以落实。

（作者为江苏省泰州市教育局教研室初中数学教研员、江苏省泰州中学附属初级中学教师）