一节公开课引发的思考

沈 婕 梁 栋

(1.天津市中小学教育教学研究室300200；2.天津市杨村第一中学 301700)

课堂教学的效果，取决于教师对教学的理解，取决于教师把教育理念、教学思想物化为教学行为的能力，这是笔者听完一节公开课后最深的感触．这节公开课的授课教师是天津市一位特级教师，学生来自天津市一所重点中学的高二年级，授课内容是“两条直线的平行与垂直的判定”(人教社A版教材必修2第三章)．

1 教学过程

1.1 学生的疑问

新课的导入和“l1∥l2⟺k1=k2”的得出一共只用了几分钟时间，教师对教材中的例3、例4没做处理，随即进入“l1⊥l2⟺k1k2=-1”的教学(研究完两条直线平行，接着研究两条直线垂直，更加紧凑流畅)．

教材中得出“l1⊥l2⟺k1k2=-1”的过程为：

设两条直线l1与l2的倾斜角分别为α1与α2(α1，α2≠90° )．

如图1，如果l1⊥l2，这时α1≠α2，由三角形任意外角等于其不相邻的两内角之和，得

α2=90° +α1，

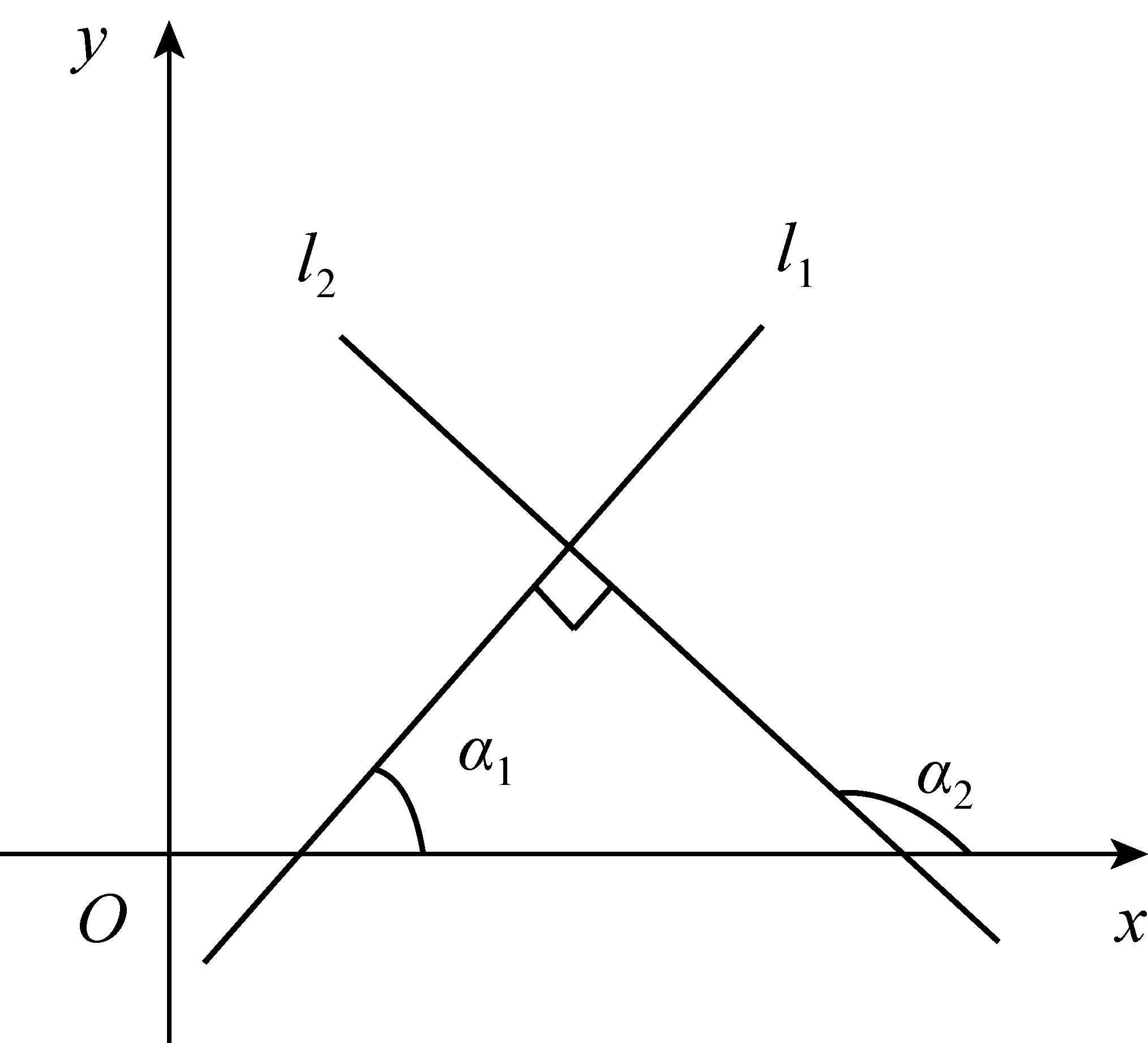
图1

因为l1与l2的斜率分别为k1，k2，且α2≠90° ，

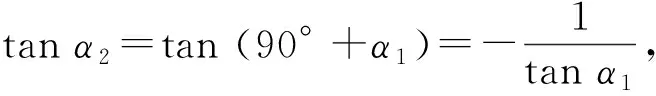
由于《普通高中数学课程标准》对余切函数不作要求，教材中也就没有

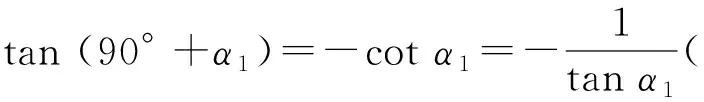
而这里又要用到这个公式，此处应是教学的一个节点．

果然，有学生提出“这个公式是怎么来的”．教师对此早有预料，教师不慌不忙地让学生自己寻找证明方法，很快有学生给出了证明：

证明的思路容易想到，证明过程也不复杂，但有学生提出，教材中的推导方法是以(*)为基础，由于以前没学过(*)，因此得到tanα2=tan (90° +α1)后，也就想不到去证明(*)，这种情况下该怎么想？

教师给出建议：直线的斜率是其倾斜角的正切，由α2=90° +α1，很自然想到转化为角的正切相等，即tanα2=tan (90° +α1)，在不知道(*)的前提下，可能不知如何对tanα2=tan (90° +α1)变形，此时可变换角度，这样想：既然求90° +α1的正切遇到困难，可以求其正弦或余弦试一试，毕竟角的正切与正弦、余弦是有密切关系的．

在教师的提示下，有学生得到了下面的方法：

由α2=90° +α1，得

sinα2=sin (90° +α1)=cosα1，

①

由α2=90° +α1，得

cosα2=cos (90° +α1)=-sinα1，

②

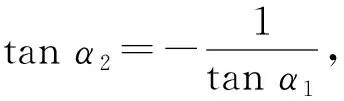
很多学生恍然大悟：原来还可以这样证明！

根据直线斜率的定义，由α2=90° +α1得到tanα2=tan (90° +α1)是第一反应，当此路不通时，转而想到①②则是深一层的反应，是思维深化的表现．

就在笔者认为问题已经圆满解决，学生的思维也被激活，应进入下一个教学环节时，提问那个学生迟疑片刻说出了自己新的困惑：我还是想不通，求角的正弦和余弦实际上也是在证明(*)，知道这个公式就容易想到证明方法，问题是我不知道这个公式，得到tanα2=tan (90° +α1)后，想不到①②，您说该怎么办？

学生的话让笔者一惊，的确，上述环节看似学生积极主动思考了，(*)的证明方法也是学生想出来的，①②求角的正弦和余弦的方法还开拓了学生的思路，按常理，教学效果已经非常好了．但冷静想一想，学生的证明也好，①②求角的正弦、余弦也罢，都是被(*)牵着走，都是为这个莫名其妙的结论寻找理由，并没有真正意义的探索！要是不知道(*)，有多少学生会想到如此变形？

1.2 学生探究

这个学生的疑问在其他同学中产生了共鸣，学生有的沉默思索，有的互相交流．

教师不动声色，向学生布置任务：既然有的同学对这种方法不太认可，那么大家就想一想，不用这个公式，能不能得出k1与k2的关系？

冷静想想，刚才学生一切活动都是围绕着教材中的方法进行的，学生的思路受“三角形任意外角等于其不相邻的两内角之和”及(*)的影响，是顺着教材思考的，如果没看到教材的方法，学生会怎么想？教室里安静下来，几分钟后，陆续有学生说出自己的想法．

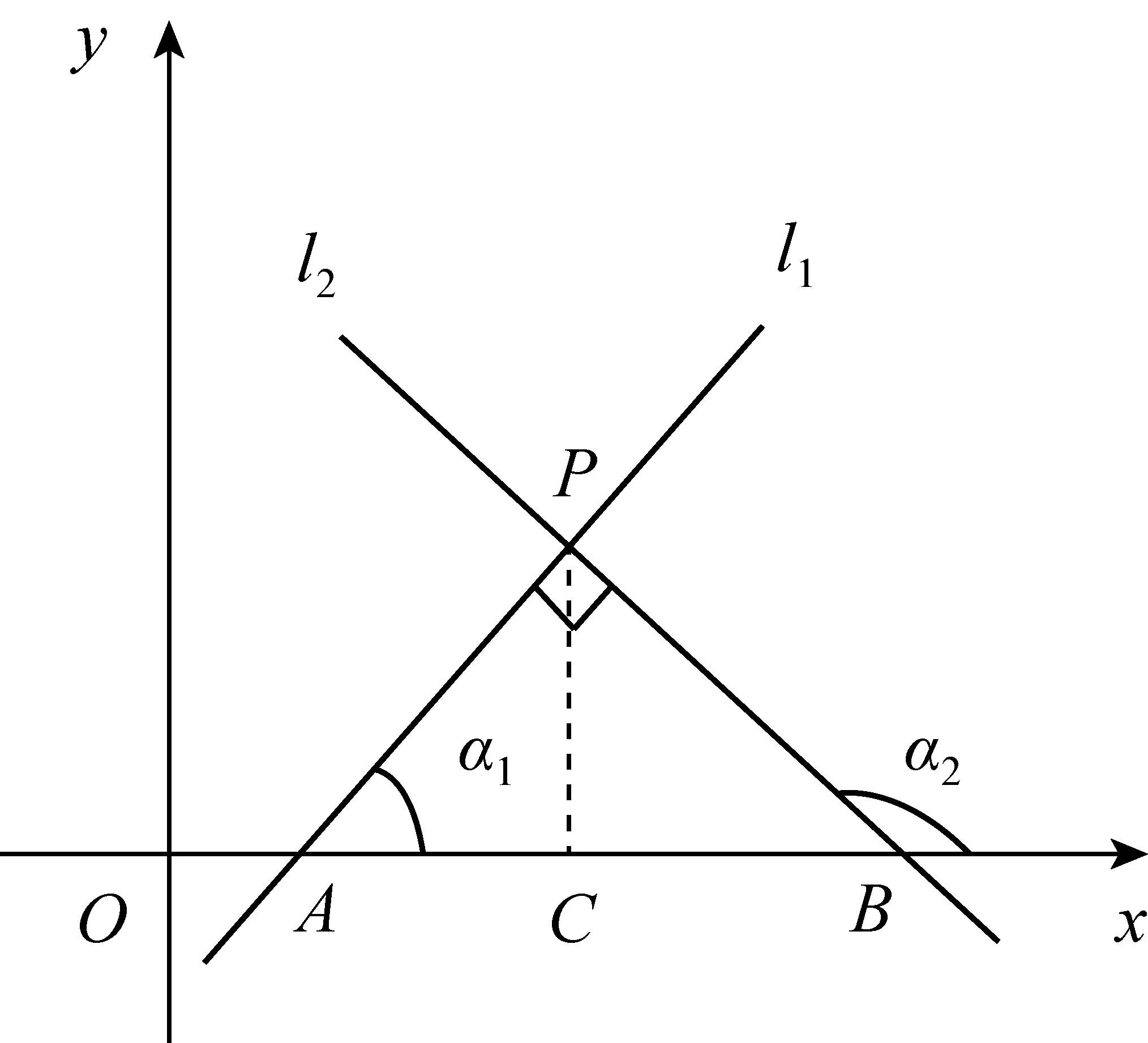
图2

思路1如图2，设l1与l2交于点P，l1与x轴交于点A，l2与x轴交于点B，PC垂直x轴于点C.

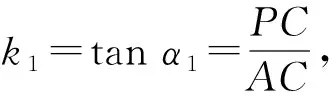
在直角三角形BCP中，

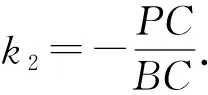
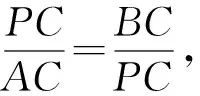
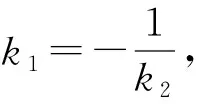
这种思路是以初中平面几何知识为基础，用到学生比较熟悉的锐角正切函数定义和相似三角形性质，tan (180° -α2)=-tanα2也是学生熟知的．

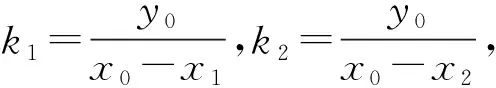
因为△PAB是直角三角形，由勾股定理得

PA2+PB2=AB2，

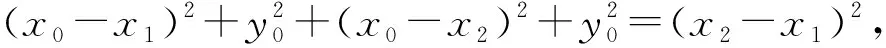
③

由于③的左边较为复杂，特征不明显，与k1，k2的关系难以迅速发现，因此学生得到③后陷入困境．

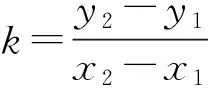
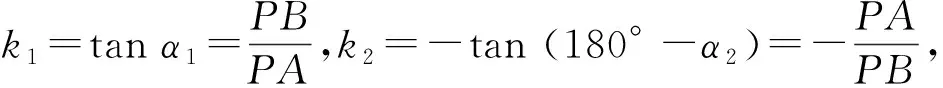
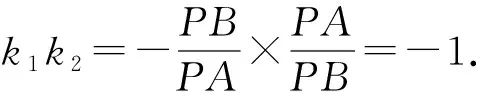
这是一种富有智慧的简捷的方法，想法虽然和思路1类似，都是利用锐角的正切函数定义，但由于是在一个“大的”直角三角形APB中考虑，k1与k2的关系一目了然，展现了宽阔的解题视野．相比之下，思路1作辅助线的方法则暴露出学生习惯借助“正规”“标准”图形思考问题的缺陷．

至此，虽然学生还在冥思苦索，但已没有新的进展．

1.3 教师点拨

教师对思路1和思路3并没有过多点评，而是在思路2的基础上稍作改进，得到新的思路．

思路4如图2，设P(x0，y0)，A(x1，0)，B(x2，0)，

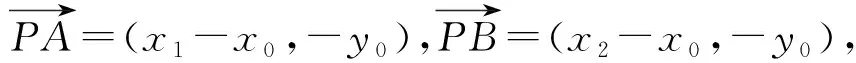
因为l1⊥l2，所以

④

④的两边同除以(x0-x1)(x0-x2)，

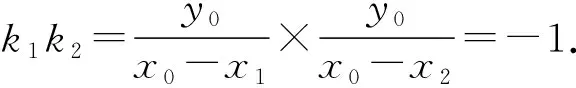
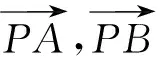
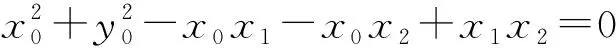
教师启发：我们得到了四种发现k1k2=-1的方法，但是教材中的方法简单直观，也是很好的思路，只因为没学过(*)就半途而废，实在可惜．能不能在α2=90° +α1的基础上得出结论呢？

提出疑问的那个学生站起来说出了自己的想法．

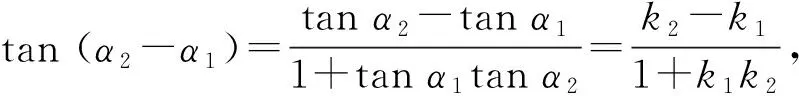
这种想法有些“大胆”，明知90° 的正切不存在，还求正切，不是“自寻死路”吗？其他学生也觉得这种想法有点不可思议，但“移项”得α2-α1=90° 又提供了一种新的思考途径，还是很有启发性的．

教师提问：90° 的正切为什么不存在？

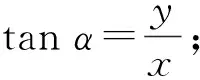
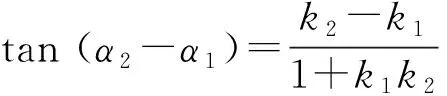
有学生不太放心：这种方法是否“严谨”？

教师总结：无论如何这是一种思考的途径，能得到结论说明有它的合理性，至于大家关心的是否严谨，回去请大家继续思考．不过，把α2=90° +α1变形为α2-α1=90° 让我们思路开阔了，这也是一种常用的变形，能不能在此基础上，找到一种你认为“严谨”的方法？

反应快的学生已经有了结果：

思路6由α2-α1=90° ，得cos (α2-α1)=cos 90° =0，

从而cosα2cosα1+sinα2sinα1=0，

又α1，α2≠90° ，

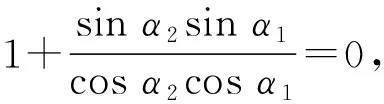
故1+k1k2=0，k1k2=-1．

……

2 课后交流

课后，笔者就关心的问题和授课教师进行了沟通交流．

(1)“l1∥l2⟺k1=k2”的教学过程几乎是“照本宣科”，这样处理是不是过于简单？

这个结论的发现和证明对学生来说没有任何难度，既然如此简单，为什么还要人为搞得复杂呢？如果教材呈现的方式好，而你又没有更好的方式，完全可以“照本宣科”．现在有一种认识，讲课时如果和教材完全一样，就显得没水平，尤其是公开课或比赛课，就更不能和教材一样，一定要搞出点花样来．这种认识是片面的，知识呈现的方式是为了让学生更容易接受，求异不是目的，不能为了求异而求异．

(2)由l1⊥l2发现k1k2=-1是个难点，教学中您并没引导学生发现这个结论，比如，用几何画板动态演示两条互相垂直的直线斜率之间的关系，或者让学生计算两条直线倾斜角分别为30° 和120° ，60° 和150° ，45° 和135° 时，k1与k2的关系，由特殊猜想出一般的结论，然后再进行证明．您是开门见山，直接让学生寻找k1与k2的关系，这样做是不是为后面的教学多留一些时间？

如果学生头脑中一片空白，发现k1k2=-1确实有一定的难度，也许还真有必要采取类似你说的方式，让学生观察、发现再证明．问题是，教师有教材，学生也有教材，每个有学习欲望的学生都很清楚预习的重要性，每个教师也会提前布置预习的作业，且不说学生获取知识的途径很多，就是翻开教材，学生一眼就能看到k1k2=-1，而且也一定看过了证明方法．如果对这一事实视而不见，还绞尽脑汁设计所谓探究问题，设置所谓的“悬念”，煞有介事地“引导”学生探究，不是浪费时间和精力吗．以您说的几何画板为例，你还没演示，学生就知道结果了，这时再提出“同学们，你们发现了什么规律？”不觉得很滑稽吗？知道结果再去发现这个结果没有任何意义．另外，演示时，学生怎么会想到要观察k1k2，而不是观察k1+k2？本节内容更适合让学生熟悉推理论证的方法．教学方法和教学重点不能离开教学内容．

尊重学生的认知基础，首先要清楚学生知道什么不知道什么，k1k2=-1学生是知道的，它就清晰地印在书上，而且还加了引起学生重视的方框．新课的导入一定要尊重事实，不能掩耳盗铃，一厢情愿．基于这种考虑，我把本节课的教学重心放在了“由l1⊥l2，推出k1与k2的关系”上，这也是本节课内容的核心所在，也是其价值所在．由于l1⊥l2有明显的几何特征，借助几何直观发现关系、推出结论是容易完成的．在这个过程中，k1与k2的具体关系并不重要，也就是说是k1k2=-1还是k1k2=-2对探索没有影响，重要的是从l1⊥l2得到k1与k2关系的思考和推理过程．

(3)公式(*)是本节课的热点，可以说没有这个公式就没有后来丰富多彩的解法．您是否想到那个学生会提出“不知道公式怎么想”的问题？几种证明的方法是否都有所准备？

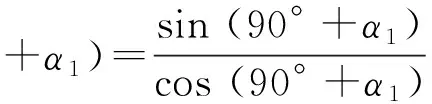
尽管证明公式不是好的问题，但还是花时间让学生证明，这是回避不了的，其中①②求角的正弦和余弦的证明方法，是为后面的探究做准备，这种准备的功效在思路6上得以体现，可以说，没有这个准备，学生不可能想到思路6，而没有思路6，前面的准备也失去意义．教学中首先要顺应学生的思维习惯，帮助学生学会思考，同时还要不断发展学生的思维，用新的方法、新的思想丰富学生的思维，促进学生不断更新、完善自己的认知结构．思路6就是基于这种考虑的产物．

至于几种证明方法，课前都有准备，但不都是自己想出来的，很多是以前的学生想出来的．课前设想只有思路3和思路4必讲，尤其是思路4，用向量的方法解决问题是一种意识，教材中虽有所涉及，但不够系统，需教师自己去总结．至于其它方法如果学生不提出来，可能略讲或不讲，一切取决于学生的需求．解题方法的呈现要有适当的时机，要有充分的理由，也就是说要讲理．

很多教师有这样一种观点，认为解题能力的培养必须通过难度大的综合题的训练才能实现，其实学习解题一定要从新授课开始，从简单题开始，这是学生最容易接受的途径，关键是教师要善于利用教材资源，挖掘其内在的教学价值．“l1⊥l2⟺k1k2=-1”是个简单问题，但通过探究得到了很多富有启发性的解决方法，其对学生思维的影响是讲几道难题、介绍几种解题方法不能相比的．没有方法不可怕，不会思考才可怕．

(4)思路4基本上是您自己包办的，在提示用向量知识后，估计多数学生能独立完成，您为什么不让学生动手完成？

教学中常常有这样的现象：学生解题遇到障碍，教师及时点拨，学生茅塞顿开，然后学生投入到后续的解题之中．学生热情高涨，积极思考，自始至终都在动脑动手，不时还有激烈的争论，最后多数学生得出正确结论．这样的一节课下来，教师讲得清清楚楚，学生听得明明白白．如此高效的课堂，学生解题能力应当很高才对，而事实是，当学生自己做题时还是不会，有时讲过几遍的题考试时仍然做错．

为什么会这样？一个重要的原因是我们忽视了思维的起点．以思路4为例，由于教材使用顺序的不同，学生在高一上学期就学习了平面向量，再加之平时应用不多，此时很难想到以其为工具推导k1与k2的关系，这里的“用平面向量知识”就是思维的起点，这个起点往往就是学生思维的障碍．他们不是不知道，而是想不到，你提示，他们就能明白，接下来的推理比较简单，他们会迅速完成，完成之后还会有一丝成就感，表面看，他们懂了、会了、掌握了，但由于思维起点是教师提示的，因此他们实际上只知道了一个数学题解法，思维并没有增进，当面对其它问题时仍不知如何处理．思路3同样如此，如果提示学生在直角三角形PAB中，如何表示tanα1和tanα2(这同样是思维起点)？学生会很快得出结论，然而，绝大多数学生自己想不到这一点．我们必须清醒地认识到，在提示下想到和自己独立想到，是有天壤之别的，提示下想到和独立想到看起来只差一点点，而这一点点恰恰就是能力．换个角度想，如果学生没看过教材，有几个学生会想到用“三角形任意外角等于其不相邻的两内角之和”？思维起点是思维过程中最重要的一环，忽视思维起点，探究的效益就大打折扣．

本节课的几种推导方法，过程都不复杂，关键是思维的起点，而思维的起点正是“为什么这样想”的问题，因此，本节课我侧重解题思路对学生思维的触发作用，多给学生提供激活思维的机会，逐步积累他们的数学活动经验．后续的推导过程一是简单，二是并非真正意义上的思维活动，学生只是在验证教师的想法，因此没给学生太多所谓动手的时间．

(5)本节课在培养学生数学素养方面是如何考虑的？

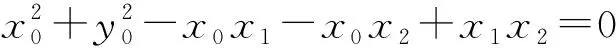
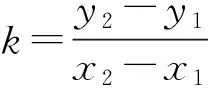
3 几点思考

课后笔者和部分学生也进行了简单交谈，笔者了解到，学生不仅预习了本节内容，而且书后的习题也做了，基本没遇到困难，但预习时只是读了两遍课本，没想那么多，上课时才发现证明“l1⊥l2⟺k1k2=-1”原来有那么多好的、简单的方法．学生普遍反映这几种思路对自己启发很大．这促使笔者对以下问题进行了思考：

(1)新授课的内容对学生来说不全是新的，教师要正视这一点，教学设计时不要在结论、结果上做表面文章，要在概念中蕴含的数学思想方法上、定理和性质证明的思考过程中设置问题，引导学生深入思考，学会思考．教学设计应简单真实．

(2)学生活动时间长不等于学生的参与度高，关键要看学生活动中动脑和动手是不是相辅相成，是不是统一的整体．在思路5中，得到α2-α1=90° 后，教师提示“既然求角的正切值行不通，那么求余弦值会怎样？大家试一试．”和教师提示“既然求角的正切值行不通，大家看看有没有其他办法？”两种提示下，学生都要动手尝试，但前者只是被动的活动，学生思维并没有真正参与，“为什么求余弦”这个重要的“思维起点”被忽视了；后者则是脑与手联动，如果学生自己意识到求余弦时，动手的活动就具有思维的含量了，如果多数学生意识不到，那么教学重心应放在引导学生发现“求余弦”上．总之，不要让学生成为验证教师想法的工具．

(3)教学方法通过教师赋予该方法的内容发挥作用，好的教学设想，如果没有好的内容支撑，就是苍白无力的空想，因此，多挖掘教学资源蕴含的教学价值是达成教学目标的必经之路.