囚禁单离子的量子阻尼运动∗

李金晴 罗云荣 海文华

(湖南师范大学物理系,低维量子结构与调控教育部重点实验室,湖南省量子效应及其应用协同创新中心,长沙 410081)

囚禁单离子的量子阻尼运动∗

李金晴 罗云荣 海文华†

(湖南师范大学物理系,低维量子结构与调控教育部重点实验室,湖南省量子效应及其应用协同创新中心,长沙 410081)

囚禁离子,阻尼运动,非厄米哈密顿，存活概率

1 引 言

随着激光冷却、整形和操控技术的发展,控制囚禁离子的量子态已成为量子信息领域的研究主题之一[1−5].通过深入研究,人们发现囚禁离子在激光冷却过程中会出现阻尼效应[6].根据阻尼产生的原因,人们尝试用不同的方法来研究阻尼囚禁离子的经典和量子运动.在经典方面,对于囚禁在开放Paul阱中的单离子,其阻尼运动可以用含阻尼项的马蒂厄方程来描述[7].而对于多离子相互作用系统,用阻尼非线性方程来描述加热现象[8,9].Duffing方程也可以用于描述囚禁离子在激光作用下的经典非线性运动[10,11].在量子方面,对于阻尼谐振子的量子化,最初考虑的是用正则变换的方法来处理[12,13].后来,Akerman等[14]用含非线性阻尼项的 Duffing振子模型很好地描述了一个单囚禁离子在多普勒激光冷却的非线性区域的稳定运动.对于量子跳跃和跃迁过程中产生的阻尼拉比振荡[15,16],可以利用主方程进行处理[17,18],反馈冷却[19]的阻尼问题也可利用主方程来解决[20].

开放量子系统常常可以用非厄米哈密顿量描述,它的复本征值不仅包含系统的能量,而且给出量子态的寿命[21].复的系统参数可以描述开放系统与外界环境交换过程中的耗散与增益[22,23]以及电子的产生和吸收[24]等现象.而PT对称的非厄米量子谐振子的研究,为实验观测非厄米系统的相干态提供了可能[25].Song等[26,27]探索了PT对称非厄米哈密顿量和相应的厄米哈密顿量之间的关系,他们发现的PT对称非厄米紧束缚格子的任意实能量本征态与相应厄米系统的共振透射态相同.对于没有PT对称的非厄米Bose-Hubbard模型,可以选取不同的系统参数来控制对于相同参数不能共存的实能量本征态之间的量子跃迁和存在虚本征能量时的衰减态存活概率的衰减速率[28,29].大量研究工作说明,非厄米哈密顿系统具有重要的物理意义[30−35].

传统量子力学原则上可以处理任何经典力学保守系统,引入非厄米哈密顿量后则可以处理任何经典力学阻尼系统[34].本文利用非厄米哈密顿量的性质,研究控制单囚禁离子的量子阻尼运动.通过对非厄米哈密顿系统进行求解,得到系统的能量本征值和相应的量子态,同时给出相应于不同态的参数区域和存活概率.当系统与外界的能量交换达到平衡时,得到实能量本征值及相应的定态,并且改变系统参数可得到不同的实能量本征值和定态.可以发现该非厄米系统外场参数能惟一确定量子稳定定态和影响波函数形态的新特征,据此提出非相干操控稳定定态之间量子跃迁的方法.当系统存在能量耗散时,得到了虚能量本征值及相应的衰减态.该情形下系统的存活概率和时间取决于能量本征值虚部的大小,从而可以通过调节系统参数来提高开放系统的存活概率.非厄米哈密顿量的位置期待值满足的运动方程和经典谐振子阻尼运动方程在形式上具有一致性.因此,采用非厄米哈密顿量来描述有阻尼的囚禁离子运动是可行的,并且控制开放系统定态之间的量子跃迁对量子信息处理具有实际意义.

2 囚禁阻尼单离子非厄米哈密顿系统的精确量子态

考虑一个囚禁在Paul阱中的单离子系统,离子的运动方向沿x轴,且受到一个沿该方向的静电场作用.考虑可用阻尼来描述的开放环境,其经典运动方程为熟知的阻尼谐振子方程[6,35]

式中λ(t)为偶极外电场项,可包含静电场和交流场;ω为谐振子的角频率;γ是经典阻尼系数.为了对该阻尼谐振子系统进行量子化,有研究者直接通过正则变换得到这个耗散系统的厄米哈密顿量[12,13],其中包含随时间指数增长的项.通常指数增长的哈密顿量是非物理的,而量子力学中,可观测量对应于厄米算符仅仅是一个充分条件而不是必要条件.因此,在λ(t)=λ(0)为时间无关的静电场时,可以用如下非厄米哈密顿量来描述该耗散系统:

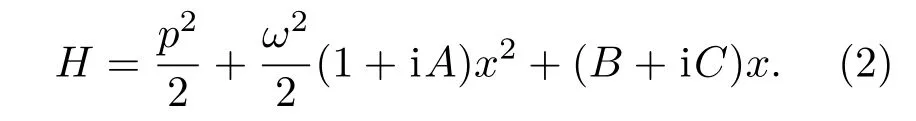
在方程(2)中,p为动量,B表示静电场强度,A和C为量子非厄米项的耗散系数,它们都是无量纲的实数.为简便计算,这里已采用自然单位进行无量纲化。同时,考虑耗散较弱的情形,即|A|≤1,|C|≤|B|.

定义“类定态”波函数ψn(x,t)=ψn(x)e−iEnt,可得非厄米哈密顿的本征方程

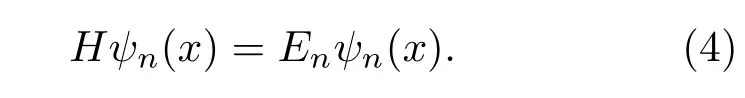
它的本征态和能量本征值分别为

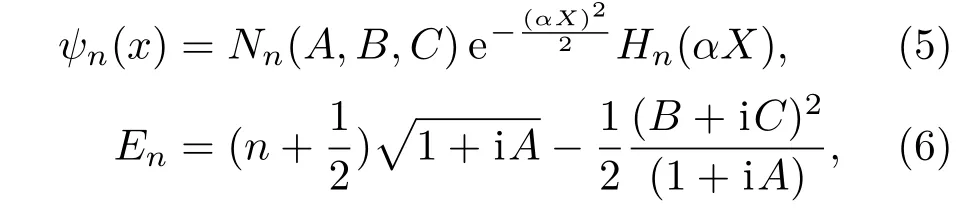
其中Nn(A,B,C)为归一化常数,Hn(αX)是自变量为αX的厄米多项式.注意到

将(5)式代入归一化条件

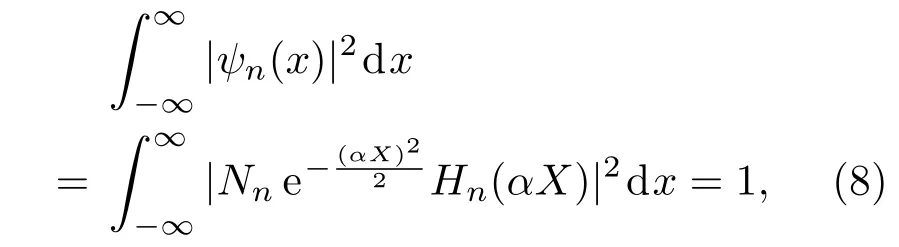
得归一化常数为

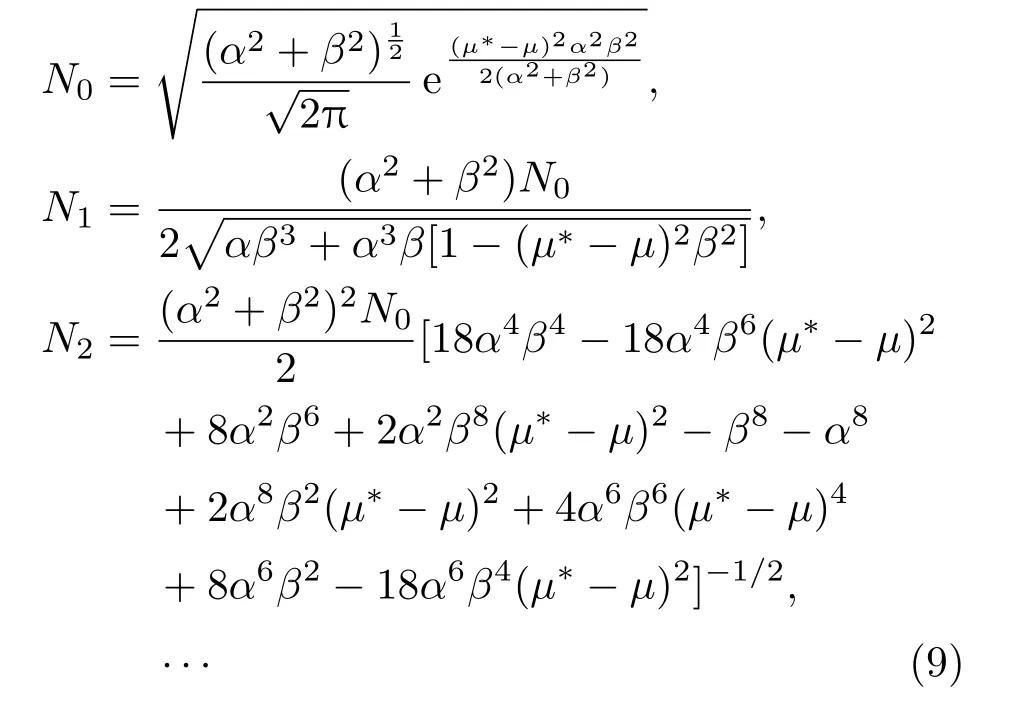
3 能谱与非厄米势能参数区域

从(6)式中可以看到,能量本征值是复数.利用

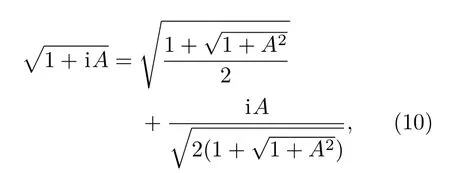
(6)式可分解成实数部分和虚数部分,即

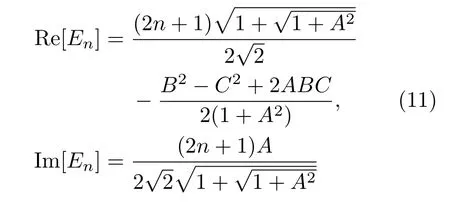
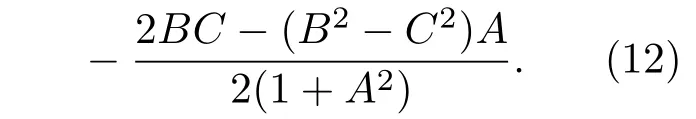
在一个开放系统中,量子系统与外部环境的能量交换是客观存在的.能量虚部大于零可导致量子态ψn(x)e−iEnt随时间指数增大,这在物理上是不被允许的[28,29].当系统的能量损失时,能量虚部小于零,量子态随时间指数衰减,离子在环境中只有一定的存活寿命.当能量虚部为零时,这个非厄米系统和外界的能量交换达到一种平衡,量子态成为不衰减的稳定定态.考虑通常的弱阻尼运动,描述耗散作用的虚数项A的绝对值应小于1,并且C的绝对值不能大于B的绝对值.通过实验调节静电场强度B,可以控制量子态的衰减率.

3.1 PT对称和不对称情形不同的实能谱与稳定量子态

在(11)和(12)式中,能量实部和虚部都是系统参数A,B,C的函数.开放环境中能量虚部为零的稳定量子态是人们最为关注的,它们存在于PT对称和不对称两种情况.例如,取A=B=0,C/=0时,非厄米哈密顿量(2)式显然是PT对称的,令(6)式中A=B=0,得能量本征值

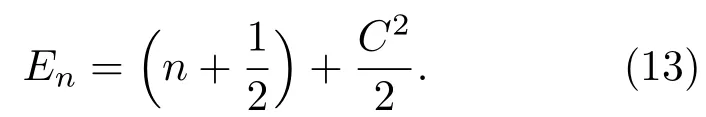
也可选取合适的系统参数A,B,C使PT不对称情形的能量虚部为零,即存在稳定量子态的条件为根据(14)式,可以分析参数A,B,C的取值与不同稳定态ψn(x)之间的关系.

在图1(a)中,取B=2为例,绘出n=0,1,2时A与C之间的函数关系图.由图1(a)可见,能量虚部为零且虚势能参数不为零时,不同稳定态对应于参数平面上不同的参数点,说明“厄米系统的一套外场参数允许存在不同定态的特征”对于该非厄米系统不再成立.取定A=0.5,图1(b)给出稳定条件(14)下C与B的函数关系.图中正方形、圆形和三角形分别表示在C=0.8处n=2,1,0态对应的不同B值.因此,利用“在一定条件下非厄米系统外场参数惟一确定量子稳定定态”的新特征,通过调节外场参数B可以控制系统在不同稳定态之间的量子跃迁.这种控制方法不同于通常的相干控制,被称为非相干控制[28].

结合(5)式、(14)式和图1,在稳定条件下,取A=B=0,C=0.3可绘出相应的PT对称时定态的概率密度图,如图2(a)所示.取B=2,C=0.3,根据(14)式算出n=0,1,2时的A值分别为0.2702,0.2193,0.1851,相应的PT不对称情形的定态概率密度如图2(b)所示.从图2可以发现一个有趣的现象,即该非厄米系统的某些定态波函数在有限区域没有零点,这与相应厄米谐振子的波函数ψn具有n个零点的性质不同.由波函数在位形空间中全体零点组成的波节图样反映了波函数的形态特征,该特征是研究量子混沌的重要途径之一[36].非厄米性导致波函数形态特征的变化,对量子混沌的研究有用.

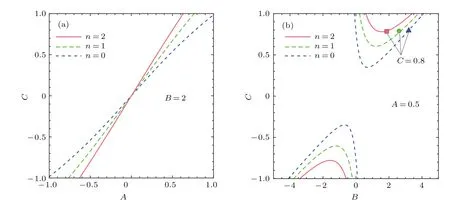
图1 在稳定条件Im[En]=0下(a)B=2情形,参数A和C之间的函数关系;(b)A=0.5情形,C与静电场强度B之间的函数关系Fig.1.Under the stability condition Im[En]=0(a)for B=2 case the relation curves of parameters A and C;(b)for A=0.5 case parameter C as a function of the static field strength B.

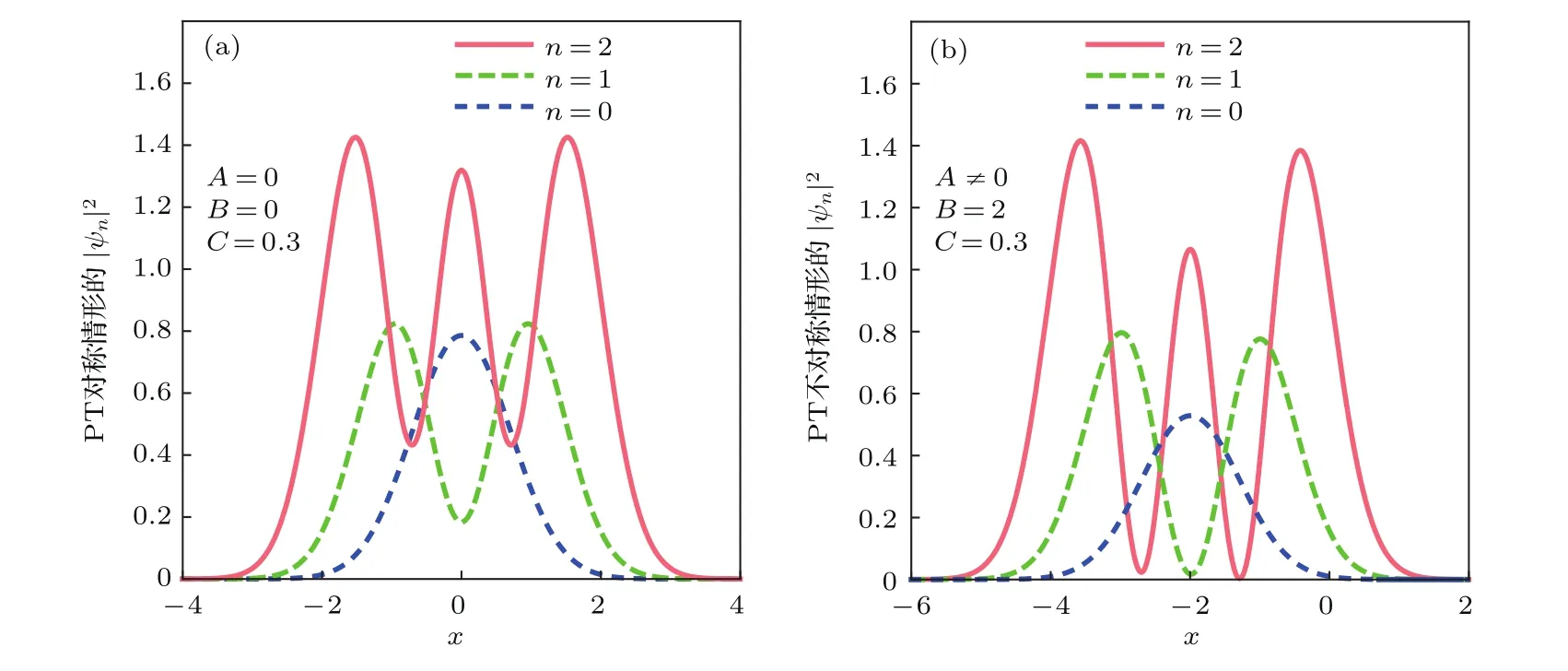
图2 几个低激发定态的概率密度分布 (a)PT对称情形,A=B=0,C=0.3;(b)PT不对称情形,B=2,C=0.3,与n=0,1,2对应的A值由(14)式确定,分别为0.2702,0.2193,0.1851Fig.2.Probability density distributions of stationary states ψn(x),n=0,1,2 for(a)the PT symmetry case with parameters A=B=0,C=0.3,and(b)the PT asymmetry case for B=2,C=0.3,and A=0.2702,0.2193,0.1851 determined by Eq.(14).

3.2 PT不对称情形的虚能谱与衰减的量子态

当能量本征值虚部小于零时,系统存在能量损耗.为了更系统地研究虚能量和参数的具体关系,根据(11)式和(12)式绘出基态(n=0)实能谱图以及与之对应的虚能谱图,如图3所示,图中的每组参数分别对应一条实线和一条虚线.在图3(a)和图3(b)中,给定其他参数,显示能量实部和虚部为A的函数,其中(a)图B=1,(b)图B=2.两图中的粗实线和粗虚线分别表示C=0时的能量实部和虚部的函数图像,而细实线和细虚线表示C=0.5时相应的函数图像.同理,在图3(c)和图3(d)中,能量实部和虚部为C的函数,前者B=1,后者B=2.两图中的粗实线和粗虚线分别表示A=0时的能量实部和虚部,细实线和细虚线表示A=−0.5时的能量实部和虚部.图3中的红色圆点是坐标轴原点.可以求得图3中不同参数对应的能量实部和虚部,例如,对于n=0,B=2,C=0.5,A分别取 0.1,0.2,0.4这三个值,相对应的能量虚部Im[En]分别为−0.7795,−0.5512,−0.1174;能量实部Re[En]分别为−1.1548,−1.4927,−1.45167. 图3中,能量虚部存在零点.当零点位于坐标轴原点上时,A=C=0,系统哈密顿量是厄米的;当零点不在坐标轴原点上,会得到前文提及的PT对称或不对称时的稳定定态和实能量值.

对于不同系统初态的存活概率可定义为[37,38]

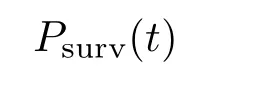
其中ψn(x,t)=ψn(x)e−iEnt是含时量子态,ψn(x,0)是归一化的初态.从(15)式中可以看出,存活概率是时间的指数函数,能量虚部的大小直接影响系统存活概率的衰减速度.对于Im[En]＞0情形,系统的存活概率大于 1,并且随时间增加趋向于无穷大,这在物理上是没有意义的.在Im[En]=0情形,存活概率恒等于1,系统处于稳定定态.Im[En]＜0的参数区域相应于图3中E0=0以下虚线上的参数,在取这些参数时,系统存活概率将随时间衰减.对于任意初态,存活概率都将最终衰减至零.同时由图3可见,对于同一A值,较大的|C|值对应于较大的负能量虚部的绝对值.对于同一C值,负能量虚部的绝对值与A的绝对值正相关.负能量虚部绝对值的增加可导致系统的耗散速率增加.因此,可以通过调节系统参数来改变能量虚部的大小,从而控制衰减态的存活概率的变化.为了分析虚能量负值的大小对存活概率衰减速度的影响,取A=0.4,0.2,0.1和C=0.5做出了衰减态ψ0(x,t)的存活概率随时间的演化图,如图4所示.从对应于B=1的图4(a)和对应于B=2的图4(b)中可以看出,对于同一B值,虚能量的绝对值越大(A值越大),衰减态的存活概率随时间衰减得更快.因此,可以通过调节系统参数来控制衰减态的衰减速度.

图3 (网刊彩色)基态能量本征值E0的实部(实线)和虚部(虚线)与A或C之间的函数关系 (a)B=1,C=0,0.5,A为变量;(b)B=2,C=0,0.5,A为变量;(c)B=1,A=0,−0.5,C为变量;(d)B=2,A=0,−0.5,C为变量Fig.3.(color online)Real(solid lines)and imaginary(dashed lines)parts of ground-state eigenenergy E0as functions of A or C for(a)B=1,C=0,0.5,A changed;(b)B=2,C=0,0.5,A changed;(c)B=1,A=0,−0.5,C changed;(d)B=2,A=0,−0.5,C changed.

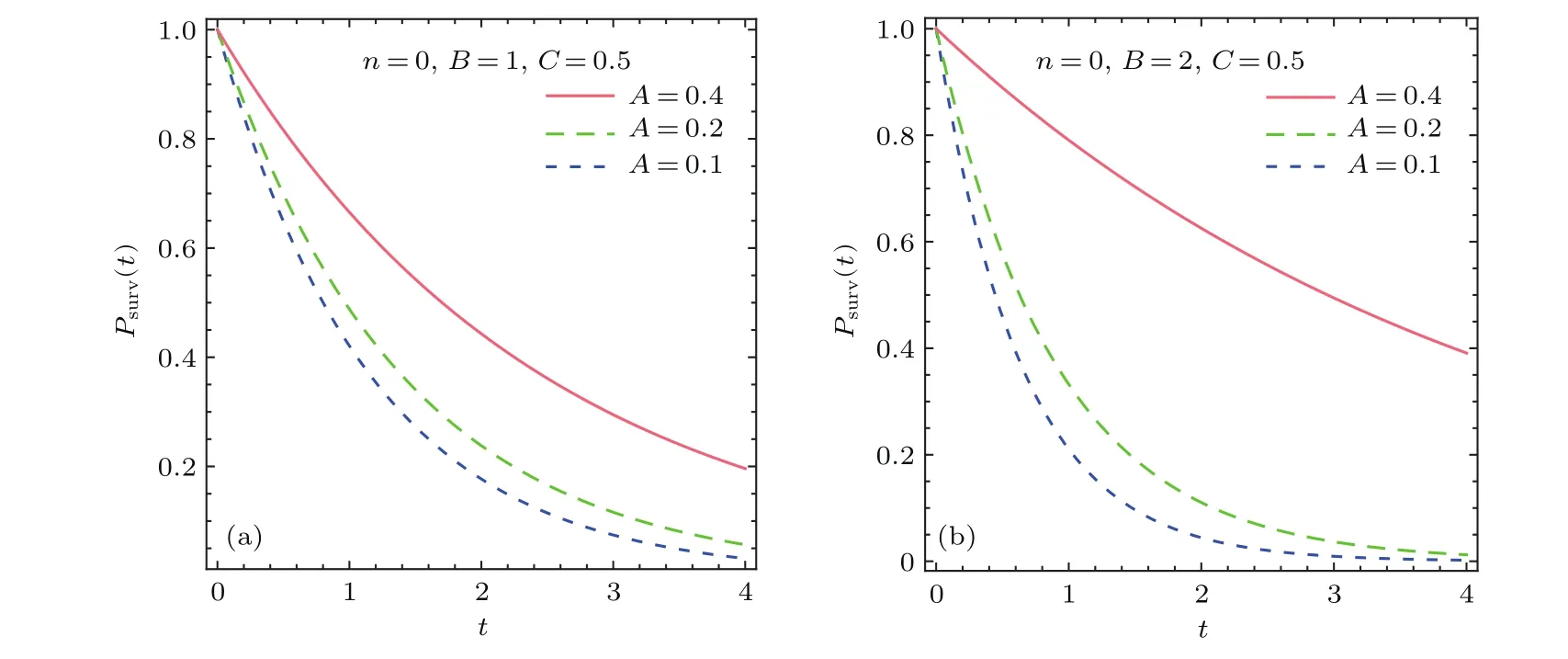
图4 衰减态ψ0(x,t)的存活概率 (a)B=1和C=0.5;(b)B=2和C=0.5Fig.4.Survival probability of the decaying state ψ0(x,t)for(a)B=1 and C=0.5;(b)B=2 and C=0.5.

3.3 虚能量的参数区域

已经证明,不同系统参数对应于不同的虚能量,不同的虚能量则对应于不同的耗散性和衰减率.为了更全面地研究系统参数A,B,C对该耗散系统的描述,以B=2为例,分别就能级n=0,1,2做对应于不同能量虚部的参数区域图,如图5所示.图中不同颜色代表不同的能量虚部值,据此可粗略看出:1)衰减所对应的能量虚部小于零的区域偏向各图的左上方;2)能量虚部为零的参数靠近从参数点(A,C)=(−1,−1)附近出发的对角线;3)能量虚部大于零的区域偏向图的右下方,相应于量子态不稳定地指数增长;4)最大能量虚部的区域和最小能量虚部的区域都随量子数n增大而增大.根据这些参数区域,可以通过调节用于冷却的激光和改变其他开放环境来粗略调节虚势能参数A,C,达到一定程度上控制量子态的目的.

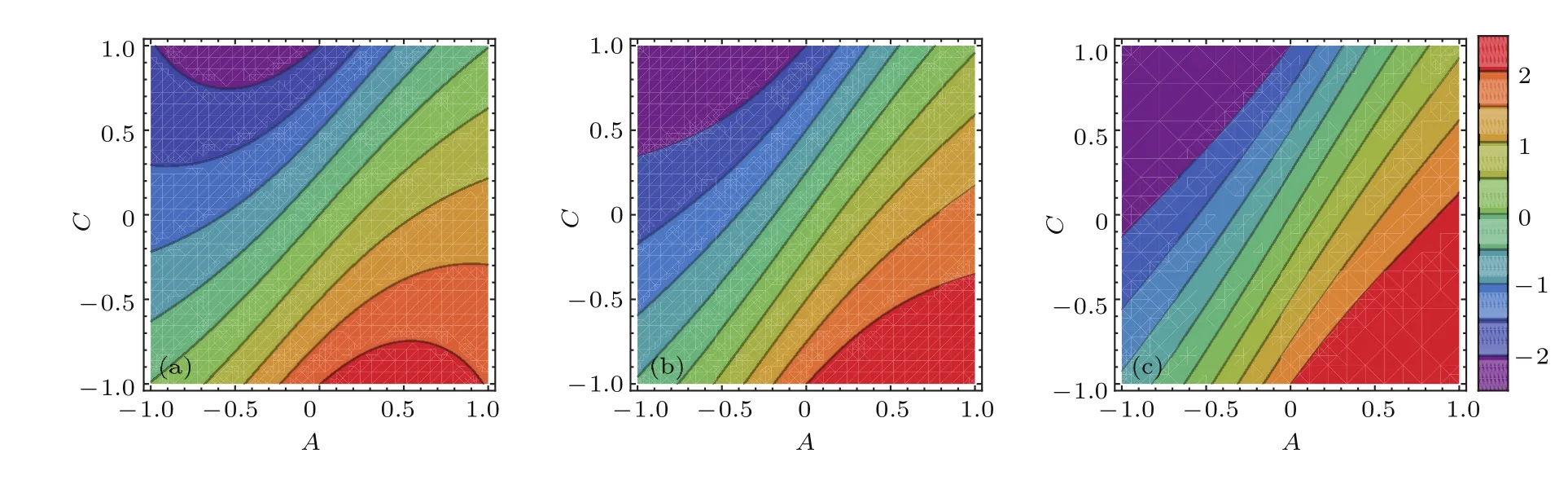
图5 (网刊彩色) 静电场强度B=2时,对应于不同能量虚部的参数区域 (a)n=0;(b)n=1;(c)n=2Fig.5.(color online)Parameter regions associated with the different imaginary parts of eigenenergies for B=2:(a)n=0;(b)n=1;(c)n=2.

4 衰减量子态与经典阻尼谐振子解的对应

已知阻尼囚禁离子的经典位移满足阻尼谐振子方程(1),根据经典-量子对应原理和谐振子相干态的性质,处于相干叠加态的量子粒子的位置期待值应满足与(1)同样的方程.利用与量子态(5)相应的一般相干叠加态可得到位置期待值为

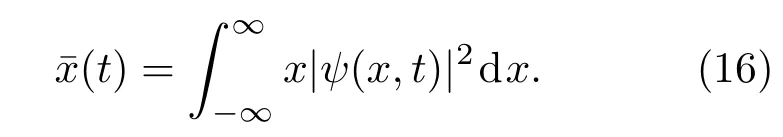
为计算简单,取系统的量子态仅为基态和第一激发态的叠加

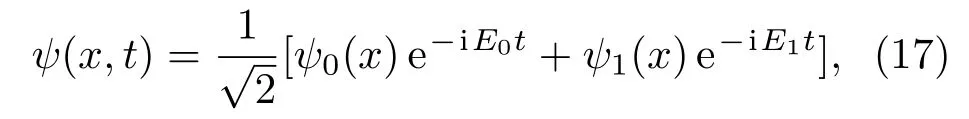
它满足初始时刻的归一化条件.将(17)式代入(16)式,积分可得到

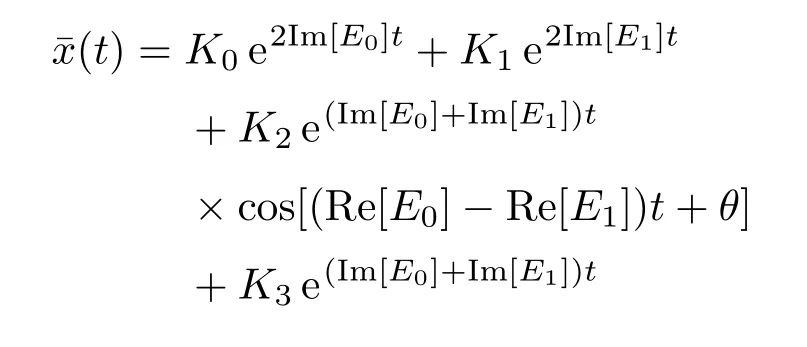
利用三角函数关系,(18)式可化简为

(18)式和(19)式中,

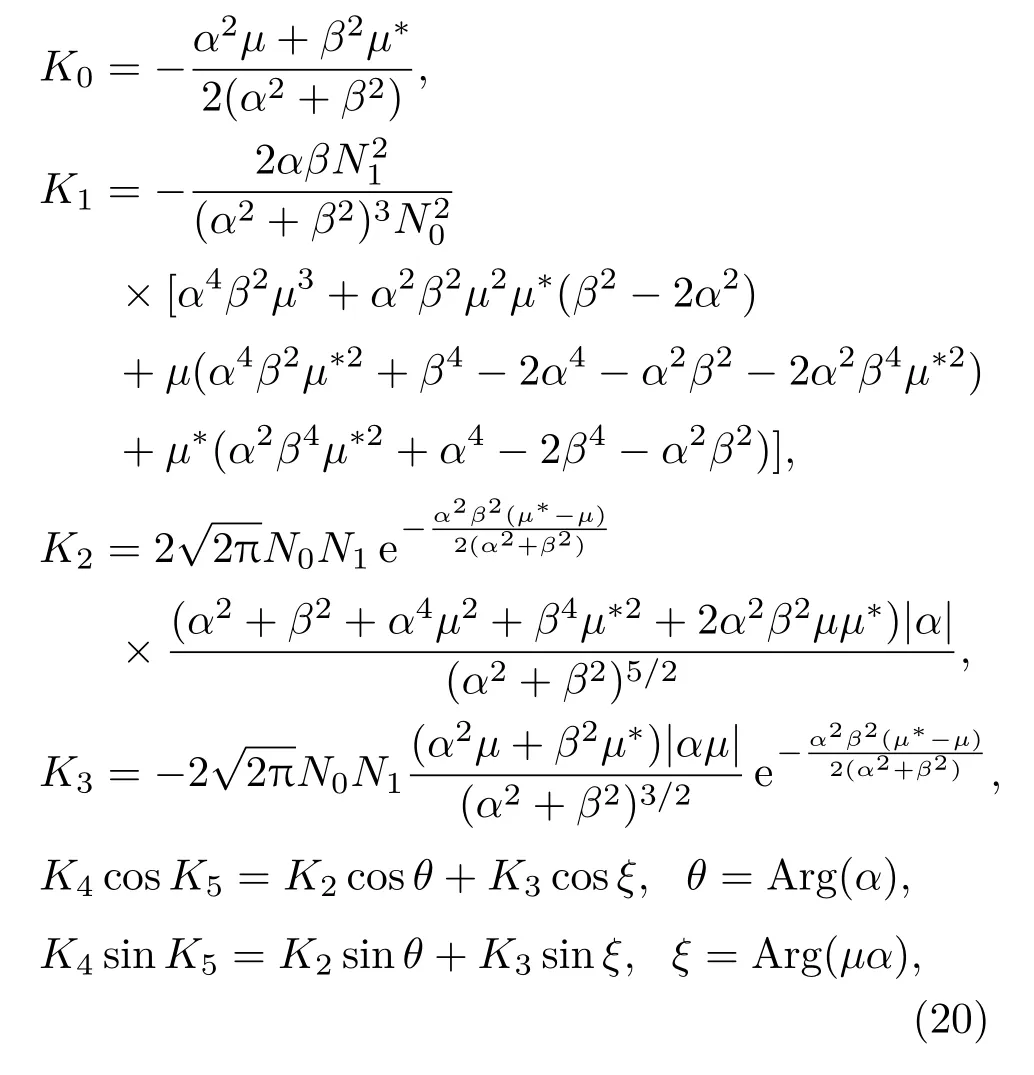
其中K0,K1,K2,K3,K4,K5,θ,ξ都为常数.然后,求位置期待值(19)式的一阶和二阶导数,消去常数K2,K3,K4,K5,θ,ξ,µ,可得阻尼谐振子方程

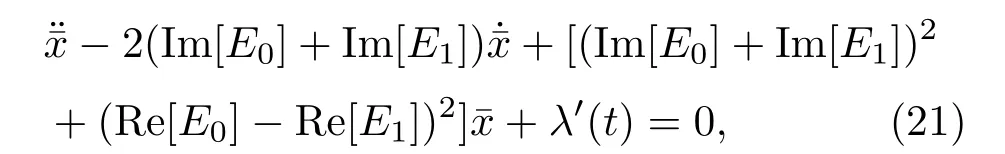
(21)式中

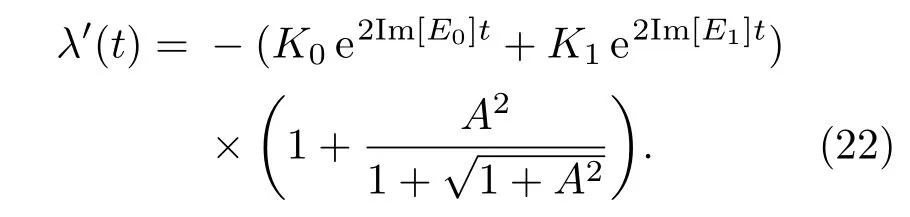
由此可见,经典阻尼运动方程和非厄米哈密顿量位置期待值的运动方程形式上是一样的.

令(21)式与(1)式一致,得到如下关系:

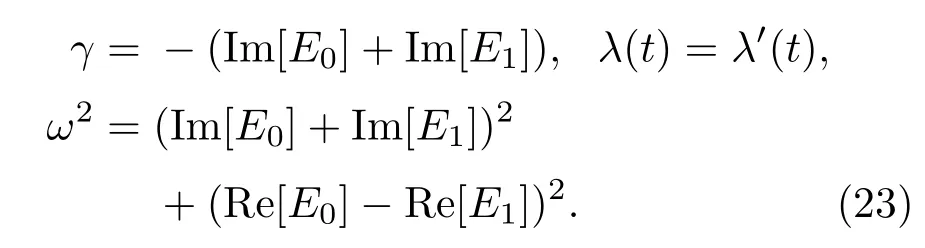
正如所料,经典阻尼系数等于能量虚部之和的负值,从而量子阻尼运动的衰减与经典阻尼运动一致;经典振子的频率ω则依赖两能量实部之差和表示阻尼系数的能量虚部.利用(22)式,选取适当的参数A,B,C,使得K0=0和Im[E1]=0或者K1=0和Im[E0]=0,从而λ是一个和时间无关的常数,对应一个受到恒力影响的经典阻尼运动,其量子动力学由非厄米哈密顿量(2)式描述.这就严格证明,λ为常数的经典阻尼振子系统(1)的量子动力学确实可以由非厄米哈密顿量(2)来支配.

5 结 论

对于一个处于开放环境中的囚禁离子,在激光冷却及与环境相互作用过程中产生的经典阻尼效应对量子动力学的影响可以用一个含有虚势能的非厄米哈密顿来描述.考虑四极囚禁势和偶极静电场下的经典运动通常用谐振子模型来描述,我们用包含偶极和四极虚势能项的非厄米哈密顿算符来描述该系统的量子阻尼运动.导出了该系统的精确本征态和本征能量,包含PT对称和不对称情形不同的实能谱与稳定量子态,以及PT不对称情形的虚能谱和衰减量子态.发现该非厄米系统外场参数可以惟一确定量子稳定定态并导致波函数形态变化等新特征,同时给出相应于不同态的参数区域和存活概率,据此提出非相干操控相应量子跃迁的方法.证实该非厄米系统中离子的位置期待值满足的运动方程和经典阻尼谐振子运动方程形式上的一致性,得到偶极和四极虚势能参数与经典阻尼参数的对应关系.所得结果将进一步丰富具有广泛应用背景的囚禁离子动力学,其中控制开放系统稳定定态之间量子跃迁的方法对量子信息处理可能具有实际意义.

根据得到的稳定定态对静电场强度B的依赖关系以及对应于不同能量虚部的参数区域,可以通过调节静电场强度来提高开放系统的存活概率以及实现稳定定态之间的量子跃迁.同时,用于冷却的激光和离子所处的开放环境也可粗略调节,这等价于调节虚势能参数A,C,通过这种调节也可达到一定程度上控制量子态的目的.本结果可以方便地推广到周期驱动的囚禁离子系统[39−43],该推广仅需让非厄米哈密顿(2)式中的偶极或四极势能参数中包含时间的周期函数,其中含时偶极势对应于方程(1)中的λ(t)项.

[1]Wineland D J 2013Rev.Mod.Phys.85 1103

[2]Duan L M,Monroe C 2010Rev.Mod.Phys.82 1209

[3]Singer K,Poschinger U,Murphy M,Ivanov P,Ziesel F,Calarco T,Schmidt-Kaler F 2010Rev.Mod.Phys.82 2609

[4]Leibfried D,Blatt R,Monroe C,Wineland D 2003Rev.Mod.Phys.75 281

[5]Soderberg K A B,Monroe C 2010Rep.Prog.Phys.73 036401

[6]DeVoe R G,Hoffnagle J,Brewer R G 1989Phys.Rev.A39 4362

[7]Blümel R 1995Phys.Rev.A51 620

[8]Nam Y S,Jones E B,Blümel R 2014Phys.Rev.A90 013402

[9]Weiss D K,Nam Y S,Blümel R 2016Phys.Rev.A93 043424

[10]Hai W H,Duan Y W,Zhu X W,Shi L,Luo X L,He C S 1997Acta Phys.Sin.46 2217(in Chinese)[海文华,段宜武,朱熙文,施磊,罗学立,何春山 1997物理学报 46 2217]

[11]Mihalcea B M,Vişan G G 2010Phys.Scr.T140 014057

[12]Peng H W 1980Acta Phys.Sin.29 1084(in Chinese)[彭桓武 1980物理学报29 1084]

[13]Gzyl H 1983Phys.Rev.A27 2297

[14]Akerman N,Kotler S,Glickman Y,Dallal Y,Keselman A,Ozeri R 2010Phys.Rev.A82 061402

[15]Fidio C D,Vogel W 2000Phys.Rev.A62 031802

[16]Gong S J,Zhou F,Wu H Y,Wan W,Chen L,Feng M 2015Chin.Phys.Lett.32 013201

[17]Bazrafkan M R,Ashra fiS M,Naghdi F 2014Chin.Phys.Lett.31 070303

[18]Klimov A B,Romero J L,Delgado J,Sánchez-Soto L L 2004Opt.Commun.230 393

[19]Jiang Z,Chen P X 2012Acta Phys.Sin.61 014209(in Chinese)[蒋智,陈平形 2012物理学报61 014209]

[20]Bushev P,Rotter D,Wilson A,Dubin F,Becher C,Eschner J,Blatt R,Steixner V,Rabl P,Zoller P 2006Phys.Rev.Lett.96 043003

[21]Eleuch H,Rotter I 2017Phys.Rev.A95 022117

[22]Dattoli G,Torre A,Mignani R 1990Phys.Rev.A42 1467

[23]Li J H,Yu R,Ding C L,Wu Y 2016Phys.Rev.A93 023814

[24]Santra R,Cederbaum L S 2002Phys.Rep.368 1

[25]Longhi S 2016Europhys.Lett.115 61001

[26]Jin L,Song Z 2009Phys.Rev.A80 052107

[27]Jin L,Song Z 2010Phys.Rev.A81 032109

[28]Zhong H H,Hai W H,Lu G B,Li Z J 2011Phys.Rev.A84 013401

[29]Xiao K W,Hai W H,Liu J 2012Phys.Rev.A85 013410

[30]Bender C M,Brody D C,Jones H F 2002Phys.Rev.Lett.89 270401

[31]Chen Z J,Ning X J 2003Acta Phys.Sin.52 2683(in Chinese)[陈增军,宁西京 2003物理学报 52 2683]

[32]Baradaran M,Panahi H 2017Chin.Phys.B26 060301

[33]Wang X Y,Chen H Z,Li Y,Li B,Ma R M 2016Chin.Phys.B25 124211

[34]Graefe E M,Höning M,Korsch H J 2010J.Phys.A:Math.Theor.43 075306

[35]Caldeira A O,Leggett A J 1985Phys.Rev.A31 1059

[36]Gu Y 1996Quantum Chaos(Shanghai:Shanghai Scientific and Technological Education Press)(in Chinese)[顾雁1996 量子混沌 (上海：上海科技教育出版社)]

[37]Casati G,Guarneri I,Maspero G 2000Phys.Rev.Lett.84 63

[38]Wimberger S,Krug A,Buchleitner A 2002Phys.Rev.Lett.89 263601

[39]Mizrahi J,Senko C,Neyenhuis B,Johnson K G,Campbell W C,Conover C W S,Monroe C 2013Phys.Rev.Lett.110 203001

[40]Chen Q,Hai K,Hai W H 2010J.Phys.A:Math.Theor.43 455302

[41]Hai K,Luo Y R,Chong G S,Chen H,Hai W H 2017Quantum Inf.Comput.17 456

[42]Chen Y H,She L,Wang M,Yang Z H,Liu H,Li J M 2016Chin.Phys.B25 120601

[43]Yang M R,Hai W H,Lu G B,Zhong H H 2010Acta Phys.Sin.59 2406(in Chinese)[杨美蓉,海文华,鲁耿彪,钟宏华2010物理学报59 2406]

Quantum damping motion of a single trapped ion∗

Li Jin-Qing Luo Yun-Rong Hai Wen-Hua†

(Synergetic Innovation Center for Quantum Effects and Applications of Hunan Province,Key Laboratory of Low-dimensional Quantum Structures and Quantum Control of Ministry of Education,Department of Physics,Hunan Normal University,Changsha 410081,China)

26 August 2017;revised manuscript

13 September 2017)

Classical motion of a single damped ion con fined in a Paul trap is usually described by a damped harmonic oscillator model.We report the treatment of quantum damping motion of the system via a non-Hermitian Hamiltonian with dipole and quadrupole imaginary potential.By deriving and analyzing the exact solution of the system,we obtain the different real energy spectra and stable quantum states for the PT symmetry and asymmetry cases,as well as the imaginary spectrum and decaying quantum state for the PT asymmetry case.The corresponding imaginary energy parameter region and the survival probability are investigated.We find that the non-Hermitian system parameters of the external filed uniquely determine the quantum stable states and lead to the new characteristic of the morphology of wave function.Based on these properties,we propose a method of incoherently manipulating quantum transitions between the quantum stable states.By setting the decayed expectation value of ion position to be the same as the decayed displacement of the classical damped harmonic oscillator,we obtain the correspondence between the imaginary potential strength and the classical damping parameters.The results will enrich the quantum dynamics of the damped trapped ions,which may be useful in a wide application field.

trapped ion,damped harmonic oscillator,non-Hermitian Hamiltonian,survival probability

PACS:37.10.Ty,46.40.Ff,03.65.—wDOI:10.7498/aps.66.233701

*Project supported by the National Natural Science Foundation of China(Grant No.11475060),the Hunan Provincial Innovation Foundation for Postgraduate and Graduate Degree Thesis,China(Grant No.CX2017B222),and the Hunan Provincial Natural Science Foundation of China(Grant No.2017JJ3208).

†Corresponding author.E-mail:whhai2005@aliyun.com

(2017年8月26日收到;2017年9月13日收到修改稿)

用包含偶极和四极虚势能项的非厄米哈密顿算符来描述Paul阱中囚禁阻尼单离子在静电场下的量子运动.通过导出和分析系统的精确解,得到在PT对称和不对称情形下的不同实能谱与稳定量子态,以及PT不对称情形的虚能谱和衰减量子态,同时给出相应于不同态的参数区域和存活概率.结果发现该非厄米系统外场参数能惟一确定量子稳定态并导致波函数形态变化,据此提出非相干操控相应量子跃迁的方法.让量子态衰减导致的离子位置期待值的衰减与经典阻尼谐振子的衰减一致,得到虚势能参数与经典阻尼参数的对应关系.所得结果将进一步丰富具有广泛应用背景的囚禁离子动力学.

10.7498/aps.66.233701∗国家自然科学基金(批准号：11475060)、湖南省研究生科研创新项目(批准号：CX2017B222)和湖南省自然科学基金(批准号：2017JJ3208)资助的课题.

†通信作者.E-mail:whhai2005@aliyun.com