基本量思想的涵义与运用
2017-12-24袁利江
袁利江
(浙江省嵊州市教育体育局教研室 312400)
在一些数学问题中,虽然涉及到许多量,但其中有几个量是可以独立取值的,而其他量则是这些量的函数.我们把任意一组可以独立取值的量作为基本量,从而数学问题就演变为仅仅研究这些基本量之间的关系了.我们提出的“基本量思想”,其操作模式的思维方式是通过减少未知量个数,以求获得问题的解的过程.它是从问题组成的若干个量出发有针对性的研究数学对象的一种思维方法.
基本原理
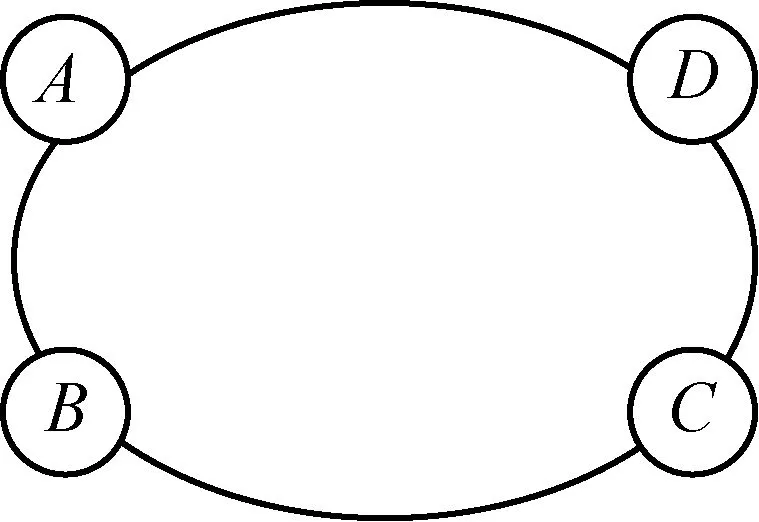
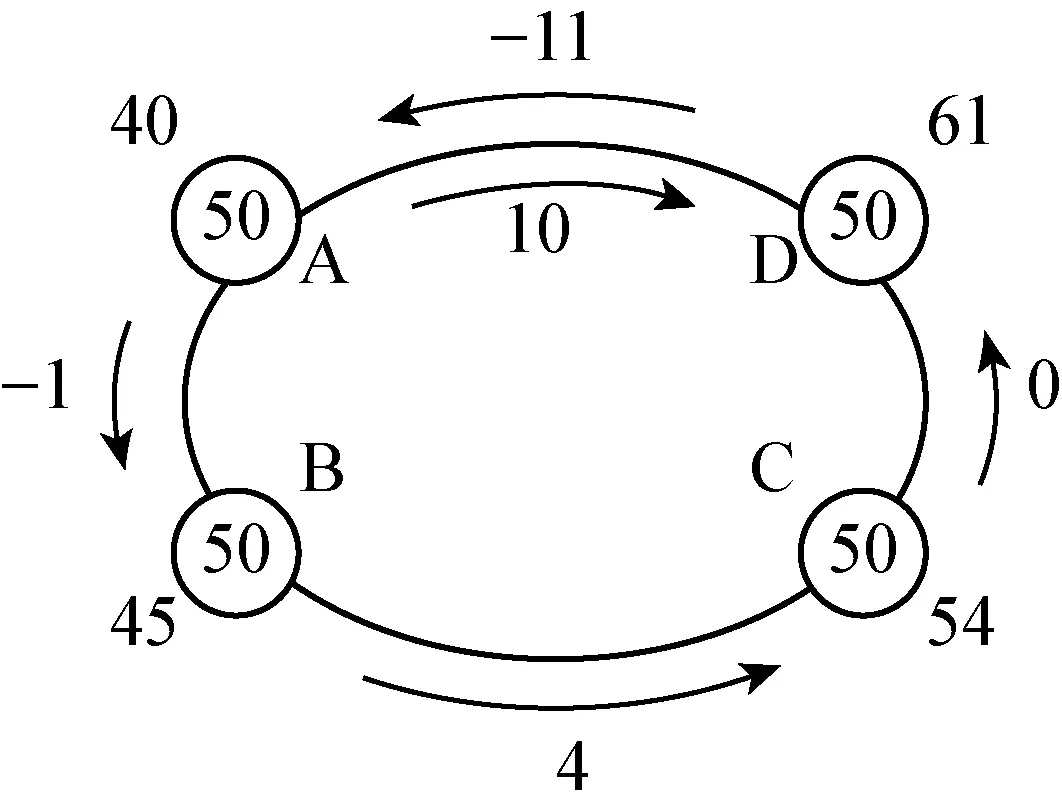
若m(m∈N*)个变量满足n(n∈N*,n 这种操作思想,具有模式化的效用,采用的方法是逐步消元,能起到化难为易、化繁为简的作用.至于选哪m-n个量作为选定的基本量,可视具体问题的研究方便而定. 例1(浙江省2016学年第一学期9+1高中联盟高三年级期中考,第8题) 已知函数f(x)=x3+ax2+bx+c(a,b,c均为非零整数),且f(a)=a3,f(b)=b3,a≠b,则c= A.16 B.8 C.4 D.1 例2(2016年北京大学博雅计划自主招生考试数学试题第5题) 若方程x2-3x-1=0的根也是方程x4+ax2+bx+c=0的根,则a+b-2c的值为( ) A.-13 B.-9 C.-5 D.前三个答案都不对 解析1设方程x2-3x-1=0的两根为x1,x2∈R,方程x4+ax2+bx+c=0的另外两个实根为x3,x4∈R,由根与系数的关系式得:x1,x2,x3,x4满足x1+x2=3,x1x2=-1,以及 解法2设x4+ax2+bx+c=(x2-3x-1)·(x2+mx+n),其中m,n∈R.于是x4+ax2+bx+c=x4+(m-3)x3+(n-3m-1)x2-(m+3n)x-n, 上述方程组共涉及5个量a,b,c,m,n,满足4个方程,从而有1个基本量,不妨选n,则a=n-10,b=-3-3n,c=-n.从而a+b-2c=-13. 点评上述解法1中,变量x1,x2,x3,x4的引入是立足于方程的实根;解法2中,则是利用了已知两方程之间的实根之间联系,而引入两个新的变量m,n.不难看出,由于变量的选择(引入)不同,使得问题解决的方式和效果也显然不同.有时为了问题达到数学化表述的需要,需要引入必要的变量,从而使得问题产生了不同的基本量选择,这也是产生“一题多解”的重要原因之一.但至少可以肯定的是,有基本量思想的指引,一定会在正确的解题线路上,即目标意识不会缺失,只是能走多远的问题罢了. 例3在等比数列{an}中,已知(a1+a4)-(a2+a3)=3,若an+1>an,求a6-a5的最小值. 所以 解法2因为(a1+a4)-(a2+a3)=3等价于(a4-a3)-(a2-a1)=3,而数列{an+1-an}是等比数列,公比也为q,故a2-a1可以看作一个独立的量. 点评从上述解法中我们不难发现,单个基本量思想运用于代数式范围或最值的确定,与函数思想有“异曲同工”之功效,其基本原理是相通的. 例4(高考题)如图是某汽车维修公司的维修点环形分布图,公司在年初分配给A、B、C、D四个维修点某种配件各50件,在使用前发现需将A、B、C、D四个维修点的这批配件分别调整为40、45、54、61件,但调整只能在相邻维修点之间进行,那么要完成上述调整,最少的调动件次(n件配件从一个维修点调整到相邻维修点的调动件次为n)为( ) A.18 B.17 C.16 D.15 解析设A→B件数为x1(x1<0时,为B→A,以下同),B→C为x2件,C→D为x3件,D→A为x4件,则 解得x2=x1+5,x3=x1+1,x4=x1-10. 故调动总件数为|x1|+|x1+5|+|x1+1|+|x1-10|. f(x1)=(|x1|+|-1-x1|)+(|x1+5|+|10-x1|)≥|x1-1-x1|+|x1+5+10-x1|=16. 当且仅当-1≤x1≤0时等号取到,故x1=0或x1=-1. 从而,有两种调动方案. (1)x1=0时,方案如下: 由x1=0,x2=5,x3=1,x4=-10得 调动件次为:0+5+1+|-10|=16. (2)x1=-1时,方案如下: 从表7可以看出,锡石多金属硫化矿主要矿石矿物的吸波能力存在显著差异,其中,脆硫锑铅矿的吸波能力最强,其次是黄铁矿,再次是锡石,闪锌矿和脉石矿物的吸波能力最差。因此,锡石多金属硫化矿主要矿石矿物的吸波能力差异奠定了锡石多金属硫化矿的微波选择性加热的基础。 由x1=-1,x2=4,x3=0,x4=-11得 调动件次为: |-1|+4+0+|-11|=16. 点评本题是一个实际问题,为了数学化,我们引进了4个变量x1,x2,x3,x4,并用这些变量将问题中的数量关系符号化,由此便得到题中的4个方程,实则3个独立性方程,从而产生1个基本量.本解法,从理论上严格论证了调动件次最少的两种方案. 例5(2016年中国奥林匹克希望联盟夏令营试题) 已知函数f(x)=x4+ax3+bx2+ax+1(a,b∈R)至少有一个零点.求a2-b的最小值. 即x0=1,a=-1,b=0,或x0=-1,a=1,b=0时,a2-b取到最小值1. 点评当基本量个数有2个时,在基本量思想的操作下,目标式被转化为二元多项式,为得到最后的解,需要对目标式进行逐个消元(即基本量)处理方能得到最后的值.本题是采用配方法达到逐个消元的目的. 例6(2017年浙江高考数学调测试卷第17题) 已知函数f(x)=x2+ax+b(a,b∈R)在区间(0,1)内有两个零点,求3a+b的取值范围. 于是3a+b=-3(x1+x2)+x1x2=(3-x1)·(3-x2)-9. 因为x1,x2∈(0,1),所以3-x1∈(2,3),3-x2∈(2,3), 于是(3-x1)(3-x2)∈(4,9), 故3a+b=(3-x1)(3-x2)-9∈(-5,0). 点评本例中,我们引进x1,x2与题中a,b共产生4个变量,根据条件共建立2个方程,从而有2个基本量.由于目标式是关于a,b的多项式,所以选择x1,x2作为基本量较为妥当.值得一提的是,本题中的条件也可以等价转换为 然后利用线性规划的有关知识求解. 分析条件方程共涉及3个量α,β,γ,满足1个方程,有2个基本量,显然选α,β为基本量后,由已知解出cos2γ较为简单,然后代入求证式的右边,再化简可得左边,从而等式成立. 点评对于条件等式的证明,往往有多种思路,有一定的难度.用基本量思想,只需将cos2γ用α,β的三角式表示后,代入目标式中化简即可,这样就把条件等式问题简化为绝对等式问题了. 3 多个(超过2个)基本量问题3.1 运用于求最值或范围 例8已知a,b,c,x,y满足ax+by+2c=0,c≠0,ab-c2≥0,求xy的最大值. 解析1此题满足2个数量关系式a+by+2c=0与ab-c2≥0,共涉及5个量,可以认定为3个基本量,可取为x,b,c. 点评求解多个基本量问题,一般采用逐步调整消元法.此题条件中共有2个数量关系(1个等式,1个不等式),出现5个变量,故有3个基本量.不等关系的介入,使得问题相对于等量关系更为复杂,变量之间相互表示也变得困难,尤其是单项式的次数是2次(甚至超过2次)时,变量之间的关系就变得更加紧密而难以分离,这在某种程度上使得部分基本量的选择失去了其该有的灵活性.也就是说,方程变为相应的不等式,会随着单项式次数的升高,使得基本量难以表示所有的非基本量,加上条件关系式又少,从而使得问题变得更为抽象复杂,而难以解决.本题中,我们利用方程解出y代入目标式,可以达到消元的目标,但不等式关系却难以实现单个参变量的代换,因为变量a,b符号的不确定性使不等式不能直接除以a或b予以实现,如本题两种解法中,目标式xy均是关于a,b,c,x的多项式,基本量虽是3个,但变量却留下了4个.所以,在解析1中,我们是对条件不等关系先进行变形,把变量a,b与b,c先整合在一起,然后整体代入,再通过逐步放缩消元得到目标式的最大值;而解析2中,我们则先利用基本量思想消去y,然后通过配方消去变量x,再利用条件不等关系ab-c2≥0放缩求得目标式的最值. 基于基本量思想的运用原理,条件等式一般是在问题求解之初使用,但在多个基本量问题中的运用,则不能循规蹈矩,需要随具体情况而论,或整合参变量,或滞后代入. 例9(中等数学2016年第7期第40页,数学奥林匹克高中训练题(205)第8题) 结合yz≥1,从而正整数y,z须满足y=z=1. 上述1个方程涉及3个量,有2个基本量,不妨选a,b. 若b≥2,则a≥b≥2,结合a≥c有 2a+b+4c+10≤7a+10≤7a+5a=12a<8ab≤8abc,矛盾; 综上所述,满足条件的六元数组(a,b,c,x,y,z)的个数为0. 数学中的思想,它可以是一种解题的方法,但又高于方法.因为数学思想是蕴涵在数学知识形成、发展和应用的过程中,是数学知识和方法在更高层次上的抽象与概括.数学知识的教学应注重背后数学思想方法的提炼与应用,重视数学思想方法的教学是数学教学者必须遵守的重要原则.当然,数学思想与数学方法也不能混为一谈.数学思想可以认为是基于思维活动概括总结得到的处理数学问题的一种基本观点,是数学策略的一种,而数学方法是指人们为了达到某种目的而采取的手段、途径和行为方式中所包含的可操作的规则或模式.它们之间的本质区别,其实就在于是否有数学思维活动的介入. 本文中提到的基本量思想,它可以理解为操作层面的一种解题方法,但其解题思维具有一定的普遍性,所以笔者称之为“思想”.“数学知识好比是人的肌肉,数学思想方法好比是人的血液,没有血液的流动,肌肉则是僵的”.借用章建跃博士的话来形容,就是道与术的关系,“道”即“思想”.我们要数学解题教学需要追求的,便是教学中的“道”!1 单个基本量问题
1.1 运用于求值


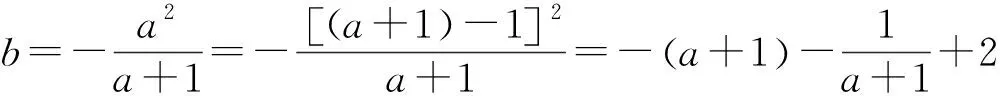



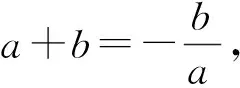
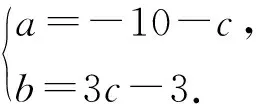

1.2 运用于确定最值或范围
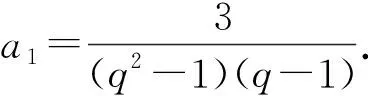



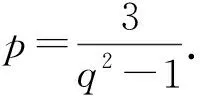
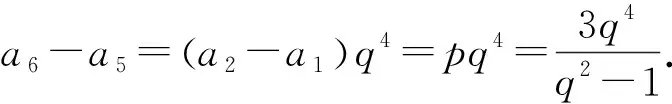
1.3 运用于解决实际问题


2 两个基本量问题
2.1 运用于求解最值或范围






2.2 运用于证明恒等式



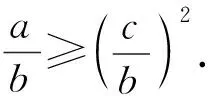


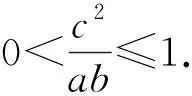


3.2 运用于确定数组个数
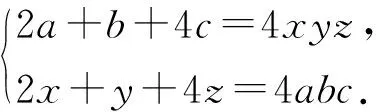




4 感悟
