有限平板共线裂纹断裂过程的数值模拟和实验研究
2017-12-23崔小朝邱选兵
彭 英, 崔小朝, 邱选兵
(1. 太原科技大学 经济与管理学院, 山西 太原 030024; 2. 太原科技大学 应用科学学院, 山西 太原 030024)
有限平板共线裂纹断裂过程的数值模拟和实验研究
彭 英1, 崔小朝2, 邱选兵2
(1. 太原科技大学 经济与管理学院, 山西 太原 030024; 2. 太原科技大学 应用科学学院, 山西 太原 030024)
采用有限元数值模拟和光弹实验方法分析了各向同性材料共线多裂纹应力场及其强度参量. 建立了有限弹性平板内三条共线裂纹计算模型, 应用ABAQUS软件的VCCT方法分析计算各向同性材料共线裂纹的裂纹尖端的应力场、 应变场分布规律及应力强度因子. 并通过光弹实验实测了6061铝板共线裂纹试件的裂纹尖端的应力强度因子. 研究结果表明, 实验和数值模拟所得的应力云图相似, 应力强度因子值基本一致, 验证了提出的应力强度因子计算模型的有效性.
多裂纹扩展; 有限平板共线裂纹; 应力强度因子; 应力云图; 光弹实验
0 引 言
工程构件中常常存在多裂纹, 而由多裂纹损伤引发的事故极具灾难性, 特别在航空、 船舶、 桥梁、 汽车等结构中多裂纹损伤问题大量存在, 已成为国内外众多学者研究的热点[1-4]. 然而, 多裂纹损伤在数学力学的求解方面一直是个难题, 其中平面弹性板中的共线裂纹问题就是多裂纹问题的一种特殊情况.
在线弹性断裂力学的研究中, 对于有限弹性平板裂纹, 应力强度因子的精确求解较为困难. 柯善明等[5]利用复应力函数法、 边界配置法等计算了有限弹性平板裂尖的应力强度因子. Muskelishvili[6]采用复变函数方法推导了裂纹应力强度因子理论公式. Zhu等[7-9]从理论和实验方面对有限大板中的单裂纹做了一系列详细的研究与探讨, 并在已有研究的基础上推导了共线裂纹的应力函数和应力强度因子的精确解析解以及相应的断裂准则. 范天佑等[10]给出了无限大板含有无穷条裂纹的复合型裂纹单向拉伸的应力强度因子的理论解. Millwater[11]和Li等[12]基于achanov’s 的方法得出了有一组共线裂纹无限大板的应力强度因子解. 樊俊铃等[13]采用ABAQUS 有限元软件建立了内聚单元模型研究I型弹塑性疲劳裂纹的扩展过程. 吴春笃等[14]利用弹塑性双参数断裂理论分析共线双裂纹之间的干涉效应. Judt等[15]基于线弹性断裂力学采用路径无关的I积分分析了平面结构中多裂纹载荷的数值计算. 郑涛等[16]研究了无限平面内三条对称的共线裂纹在双向压缩载荷下的应力强度因子, 并根据复变函数理论推导了裂尖应力强度因子的精确解析解, 并通过光弹实验研究验证了裂纹应力强度因子与裂纹间距的关系.
以上的研究主要是针对于无限大板的各种裂纹分析, 鲜有针对有限宽板含共线穿透裂纹情况的相关研究. 本文将采用有限元数值模拟结合光弹实验方法求解有限弹性板内含有三条共线裂纹的应力强度因子, 探讨其研究方法.
1 裂纹尖端应力场理论计算
设无限大板有三条共线穿透裂纹, 如图 1 所示. 垂直于裂纹方向受单向均匀拉伸作用, 裂纹长度为2a, 内裂纹中线距外裂纹中线的距离为2b. 由应力强度因子理论得知: 其外裂纹内尖端(A点)的应力强度因子表达式为[17]

图 1 无限大板含有共线裂纹Fig.1 The collinear cracks of infinite plate
对于有限宽板含共线穿透裂纹情况目前还未见相关的理论结果. 鉴于此, 对于有限宽板的研究分析, 本文采用数值模拟和光弹实验相结合的方法进行分析.
2 有限元数值模拟
根据有限元方法, 采用ABAQUS分析软件, 对含有共线裂纹的有限宽板条进行数值建模和模拟分析. 模型的长、 宽、 厚依次为250, 40, 2 mm, 材料为6061铝板, 材料属性如表 1 所示. 其底边固定, 给顶边施加y向位移, 对模型进行网格划分, 并采用虚拟裂纹闭合法(VCCT)求解裂纹尖端的能量释放率, 通过能量释放率与应力强度因子的关系得到裂纹尖端的应力强度因子.

表 1 材料属性Tab.1 Material properties
2.1 裂纹扩展不同位移的应力


图 2 不同加载位移时的Mises应力云图 Fig.2 Mises stress nephogram of the variable loading distance
2.2 能量释放率和应力强度因子随加载历程的变化
能量释放率与应力强度因子的关系可以表示为[18]
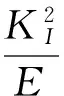
图 3 为模拟计算的能量释放率和应力强度因子随加载历程的变化曲线. 从图 3 可以看出: 在此加载条件下, 裂纹的扩展是一个非稳态的扩展过程. 在裂尖的应力强度因子达到KIC后, 裂纹开始扩展.
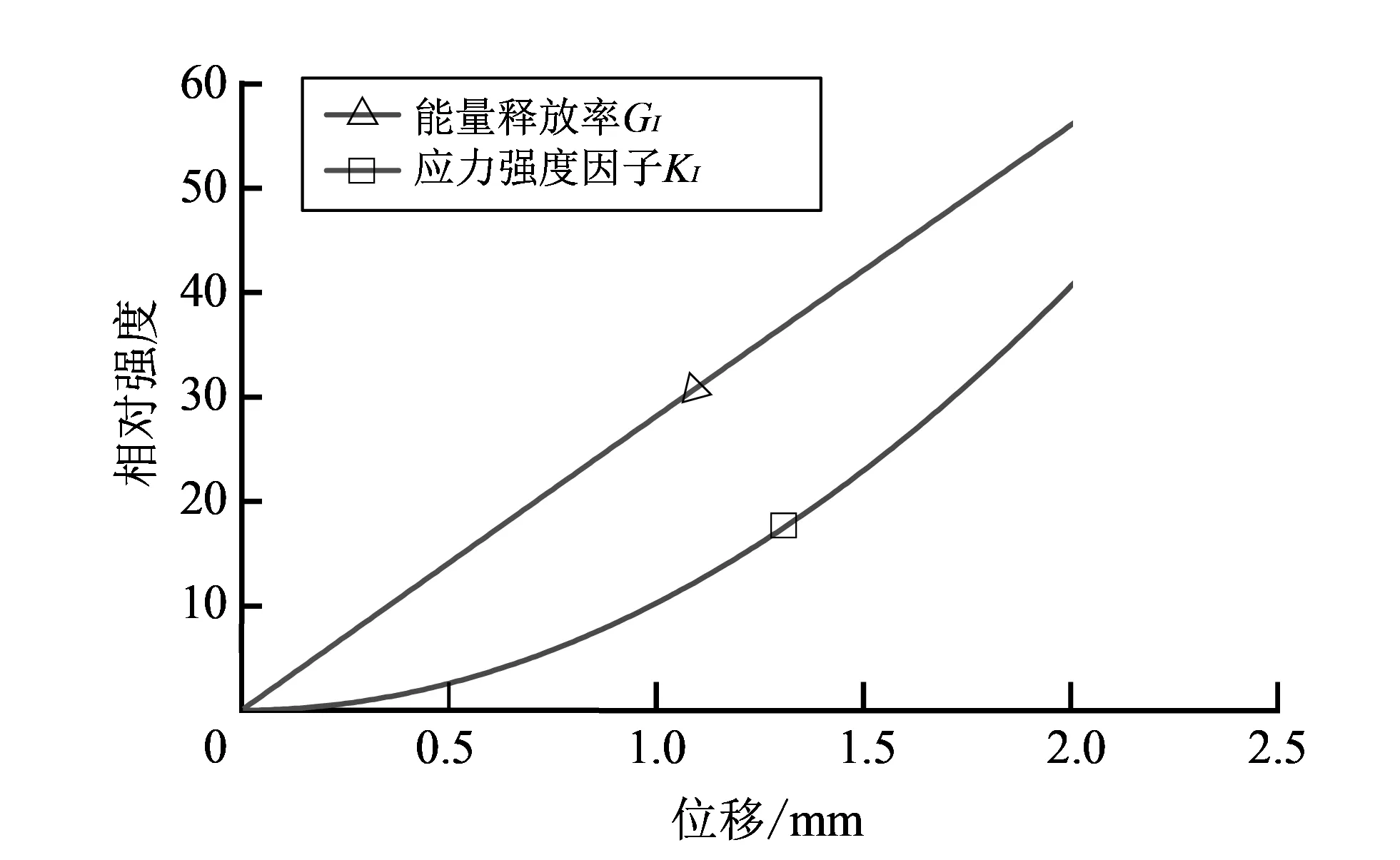
图 3 能量释放率和应力强度因子随加载历程的变化曲线Fig.3 Energy release rate and stress intensity factor versus the loading history
3 光弹实验研究
3.1 实验原理
采用光弹贴片法对共线裂纹构件进行实测. 贴片法中, 条纹级数反映的是构件测点主应变差[19]
式中:n为条纹级数;hc为贴片的厚度;fc为贴片材料的应变条纹值, 采用拉伸试验可以得到fc=345.7 cm·με/级.
用测点的应变分量εx,εy,γxy表示主应变ε1,ε2, 代入式(4)可得
由线弹性断裂力学知, 张开型裂纹尖端附近的应力场表达式为[20]
根据广义胡克定律, 可得
联立式(5)~(7), 可得名义应力强度因子公式

3.2 实验过程与结果分析
试件尺寸与模拟仿真部分一致, 采用聚碳酸酯材料作为贴片, 贴片厚度为1 mm. 贴片单侧镀银膜以提高贴片的反射率, 用环氧xy-508胶将贴片粘贴在构件中央, 将制作好的模型通过雕刻技术在构件中间开设长度为3 mm的三条共线裂纹, 裂纹间距7.75 mm, 用平板夹头夹持在万能实验机上连续拉伸, 实验装置如图 4 所示.

图 4 光弹实验装置Fig.4 The photoelastic experimental setup

图 5 不同加载时刻下的光弹等差线条纹图Fig.5 The photoelastic isochromatic fringe for the variable loading history
将贴片构件夹持在万能实验机上, 万能试验机由计算机控制加载. 并使用反射式光弹仪, 在白光光源的正交圆偏振光场下逐渐加载. 当条纹达到五级后, 改用单色光源, 继续加载使裂纹尖端出现更多级条纹, 观察裂纹边缘的等色线条纹变化情况, 并用数码设备记录变化过程.
采用图4(b)的实验装置, 在万能实验机加载的过程中, 随载荷逐渐增大, 采集到的光弹等差线条纹图如图 5 所示. 从图 2, 图 3和图 5 可以看出, 数值模拟所得的应力场和实验实测应力场相似.
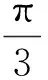
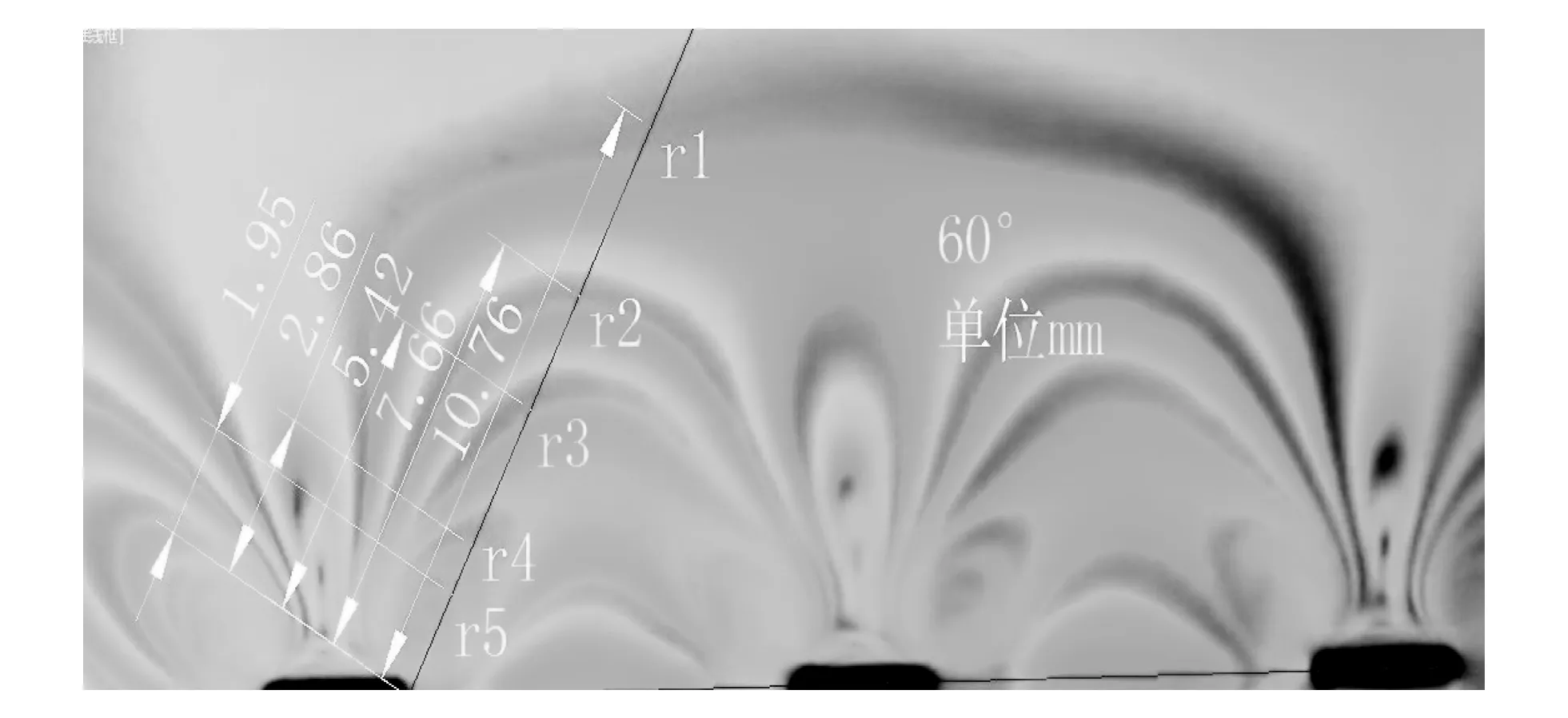
图 6 沿径向变化的条纹级数Fig.6 The fringe pattern along the radial changing direction
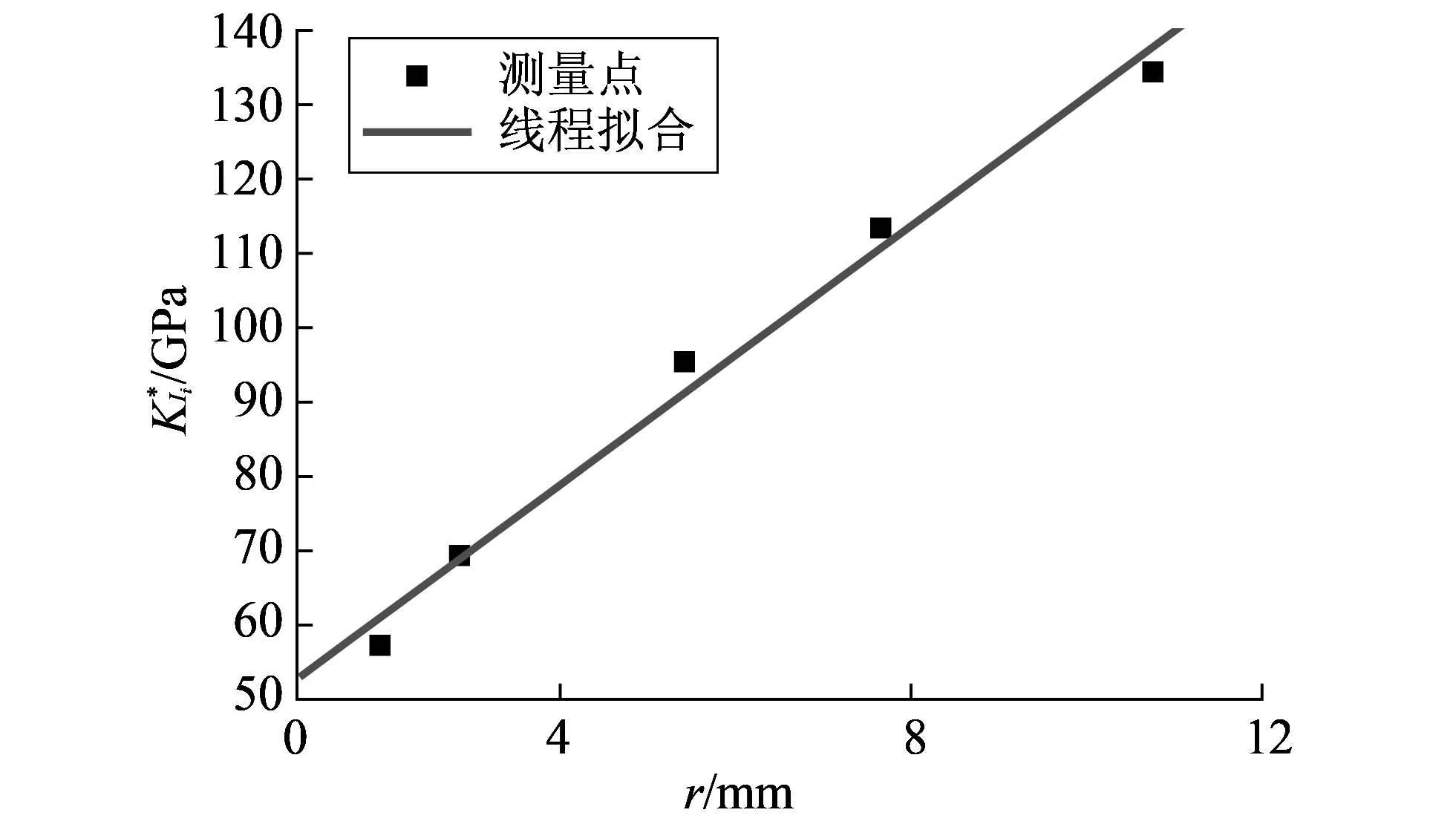
图 7 60°拟合应力强度因子Fig.7 The fitting stress intensity factors along with 60°

4 结 论
本文通过对有限弹性板内含有共线裂纹铝板的有限元数值模拟及光弹试验研究, 分析计算了共线裂纹尖端的应力强度因子, 得到如下结论:
1) 数值模拟和实验所观察到的应力云图形状基本一致, 所得到的应力强度因子值也比较吻合, 说明数值模拟和实验相结合的方法是研究多裂纹问题的有效方法.
2) 裂尖应力强度因子的计算, 除了解析法和数值解法以外, 有时用实验测定更为方便、 直观. 在实验中虽然不能直接测定断裂参数, 但可以通过和某一可测量的量(如位移、 应变、 应力等)之间的关系来求得. 本文采用反射光弹实验方法, 不受试件材料的限制, 且具有全场性. 实验误差产生的原因可能有以下几方面: 实验模型加工不够精确; 实验数据采集存在误差, 尤其对于较稀疏的条纹图更为严重.
[1] Singh I V, Mishra B K, Pant M. An enrichment based new criterion for the simulation of multiple interacting cracks using element free Galerkin method[J]. International Journal of Fracture, 2011, 167(2): 157-171.
[2] Cen Z, Maier G. Bifurcations and instabilities in fracture of cohesive-softening structures: a boundary element analysis[J]. Fatigue & Fracture of Engineering Materials & Structures, 2007, 15(9): 911-928.
[3] 黄达, 黄润秋. 卸荷条件下裂隙岩体变形破坏及裂纹扩展演化的物理模型试验[J]. 岩石力学与工程学报, 2015, 29(3): 502-512.
Huang Da, Huang Runqiu. Physical model test on deformation failure and crack propagation evolvement of fissured rocks under unloading[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 29(3): 502-512. (in Chinese)
[4] 陈康, 许希武, 郭树祥. 双向梯度复合材料裂纹尖端应力强度因子研究[J]. 航空学报, 2013, 34(8): 1832-1845.
Chen Kang, Xu Xiwu, Guo Shuxiang. Stress intensity factors at crack tips in two-directional graded composites[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(8): 1832-1845. (in Chinese)
[5] 柯善明, 顾浩鼎. 裂纹端部的力学研究[J]. 东北地震研究, 1994, 10(2): 1-12.
Ke Shanming, Gu Haoding. Mechanical research at the end of cracks[J]. Seismological Research of Northeast China, 1994, 10(2): 1-12. (in Chinese)
[6] Muskhelishvili N I. Some basic problems of the mathematical theory of elasticity[M]. Netherlands: Springer, 1977.
[7] Zhu Z, Wang L, Mohanty B, et al. Stress intensity factor for a cracked specimen[J]. Eng. Fracture Mech., 2005(73): 482-489.
[8] Zhu Z. Evaluation of the range of horizontal stresses in the earth’s upper crust by using a collinear crack model[J]. Journal of Applied Geophysics, 2013, 88: 114-121.
[9] Zhu Z. An alternative form of propagation criterion for two collinear cracks under compression[J]. Mathematics and Mechanics of Solids, 2009, 14(8): 727-746.
[10] 范天佑. 断裂理论基础[M]. 北京: 科学出版社, 2003.
[11] Millwater H R. A simple and accurate method for computing stress intensity factors of collinear interacting cracks[J]. Aerospace Science and Technology, 2010, 14(8): 542-550.
[12] Li Y, Tham L, Wang Y, et al. A modified Kachanov method for analysis of solids with multiple cracks[J]. Engineering Fracture Mechanics, 2003, 70(9): 1115-1129.
[13] 樊俊铃, 郭杏林. 弹塑性疲劳裂纹扩展行为的数值模拟[J]. 机械工程学报, 2015, 51(10): 33-40.
Fan Junling, Guo Xinglin. Numerical simulation on elastic-plastic fatigue crack growth behavior[J]. Journal of Mechanical Engineering, 2015, 51(10): 33-40. (in Chinese)
[14] 吴春笃, 王钟羡, 焦广臣. 共线裂纹弹塑性双参数断裂分析[J]. 机械强度, 2011, 33(4): 597-600.
Wu Chundu, Wang Zhongxian, Jiao Guangchen. Elastic-plastic fracture analysis of double co-linear cracks withJ-A2method[J]. Journal of Mechanical Strength, 2011, 33(4): 597-600. (in Chinese)
[15] Judt P O, Ricoeur A. Crack growth simulation of multiple cracks systems applying remote contour interaction integrals[J]. Theoretical & Applied Fracture Mechanics, 2015(75): 78-88.
[16] 郑涛, 朱哲明, 金文城, 等. 压缩荷载下3条对称的共线裂纹应力强度因子的解析解[J]. 四川大学学报(工程科学版), 2013, 45(S1): 58-62.
Zheng Tao, Zhu Zheming, Jin Wencheng, et al. Analytical solution of stress intensity factor for three symmetric collinear cracks under compression[J]. Journal of Sichuan University (Engineering Science Edition), 2013, 45(S1): 58-62. (in Chinese)
[17] 中国航空研究院. 应力强度因子手册[M]. 北京: 科学出版社, 1993.
[18] 刘梦和, 王向东, 邵兵. Ⅰ-Ⅱ复合型裂缝应力强度因子和应变能释放率的关系[J]. 水利水电科技进展, 2012, 32(6): 31-33.
Liu Menghe, Wang Xiangdong, Shao Bing. Relationship between stress intensity factor and strain energy release rate of Ⅰ-Ⅱ mixed mode cracks[J]. Advances in Science and Technology of Water Resources, 2012, 32(6): 31-33. (in Chinese)
[19] 阮孟光. 光测力学[M]. 北京: 北京航空航天大学出版社, 1995.
[20] 卿海, 杨卫, 吕坚. 多条表面裂纹相互作用的应力分析[J]. 工程力学, 2009, 26(1): 1-6.
Qing Hai, Yang Wei, Lü Jian. Stress analysis of multiple surface cracks with interactions[J]. Engineering Mechanics, 2009, 26(1): 1-6. (in Chinese)
NumericalSimulationandExperimentalStudyonCollinearCracksFractureoftheFinitePlate
PENG Ying1, CUI Xiao-chao2, QIU Xuan-bing2
(1. School of Economy and Management, Taiyuan University of Science and Technology, Taiyuan 030024, China;2. Applied Science College, Taiyuan University of Science and Technology, Taiyuan 030024, China)
The stress field and strength of the multiple cracks propagation of isotropic material were analyzed by using finite element numerical simulation and photoelastic experiment. The computational model of the tri-linear collinear cracks was established for the finite elastic plate. The stress intensity factors (SIFs), stress field distribution and propagation stress nephogram of the crack tips were computed and analyzed by using virtual crack closure technique (VCCT) numerical solution in ABAQUS. Meanwhile, they were measured and validated by using the photoelastic experiment of the model 6061 aluminium sample with collinear cracks. The study results indicate that the stress intensity factor and propagation stress are identical in the experiment and simulation, the propagation direction and tendency also agree with each other. So the proposed approach for SIFs is effectively verified.
multiple cracks fracture; collinear cracks of finite plate; stress intensity factor; stress nephogram; photoelastic experiment
1673-3193(2017)05-0639-06
2016-11-24
国家自然基金资助项目(51574171); 山西省高等学校科技创新项目(2015166)
彭 英(1978-), 女, 讲师, 博士生, 主要从事材料设计及力学行为研究.
TP277
A
10.3969/j.issn.1673-3193.2017.05.023
