参数情形下第一类曲面积分的计算

任一雄1 ，徐怀

(1.安徽大学物理与材料科学学院，安徽 合肥 230039；2.安徽大学数学学院，安徽 合肥 230039)

参数情形下第一类曲面积分的计算

任一雄1，徐怀2

(1.安徽大学物理与材料科学学院，安徽 合肥 230039；2.安徽大学数学学院，安徽 合肥 230039)

第一类曲面积分有着广泛的运用。主要研究当曲面是以参数方程的形式给出时面积微元的计算方法，一种方法是采用法向量投影的思路，另外一种是直接计算曲面面积微元的方法，得出相同的结果。最后给出几个数值的例子。

第一类曲面积分；二重积分；参数方程

(1)

类似地，依据不同的曲面方程，还可以在XoZ,或YoZ平面上计算这个第一型曲面积分， 在此不再赘述。

我们自然地考虑一个推广情形，就是曲面方程是个参数方程时，如何计算这个第一型曲面积分，也就是能否把曲面投影到任何一个参数平面上，进而计算积分结果。在下文中将给出在任意参数平面上的计算公式，并给出两种证明方法，最后给出两个数值计算例子。

1 主要结论

定理设曲面S由如下参数方程描述：S:x=f(u，v),y=g(u，v),z=h(u,v),(u,v)∈D,

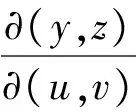
(2)

其中：

证明：

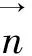
容易得到雅可比式：

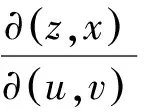
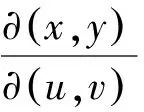
代入化简得：

因此曲面的面积微元为：

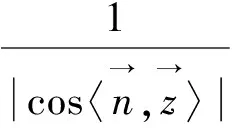
此时的第一型曲面积分的计算公式可表示为：

下面给出另外一个证明方法：

(方法2)取(u,v)坐标下的两组平行的线，它们之间的差分别为Δu,Δv，在曲面S上分别交于四个点M1,M2,M3,M4，面积微元也就是也就是求四边形M1M2M3M4的面积，四点的坐标分别是：

M1:

x1=f(u,v)

y1=g(u,v)

z1=h(u,v)

M2:

x2=f(u+Δu,v)

y2=g(u+Δu,v)

z2=h(u+Δu,v)

M3:

x3=f(u+Δu,v+Δv)

y3=g(u+Δu,v+Δv)

z3=h(u+Δu,v+Δv)

M4:

x4=f(u,v+Δv)

y4=g(u,v+Δv)

z4=h(u,v+Δv)

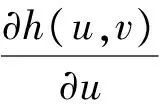
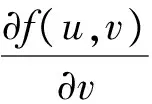
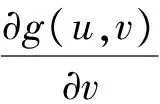
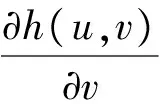
应用向量的矢量积并略去高阶无穷小得出面积微元的近似值为:

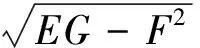
注:

(1)两种证明方法都得到了同样的面积元素，思考方式却截然不同。第一种方法我们将曲面投影在我们熟知的直角坐标系中，再由二重积分的换元公式得到(2)。第二种方法直接采用空间向量方法，应用向量的矢量积，得到曲面面积微元的表达式。定理表明可以建立空间曲面的参数方程，在计算第一型曲面积分时，这样选择恰当的曲面参数方程，可以大大简化我们的计算[6-7]。

(2)特别的当曲面方程为z=fx,y时，此时曲面的参数方程可视为S:x=x,y=y,z=f(x,y),(x,y)∈D。

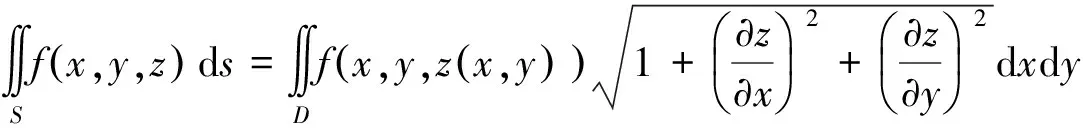
可见(2)式是(1)式的一个推广，(1)式是(2)式的一个特例。

2 数值例子

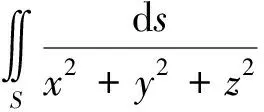
解：我们可以应用参数方法的公式

设x=Rcosu,y=Rcosu,z=v，其中u∈(0,2π),v∈(0.H)

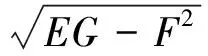
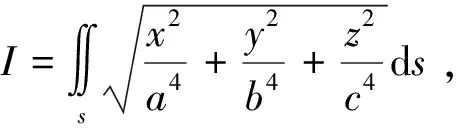
解：椭球面参数方程可写为：

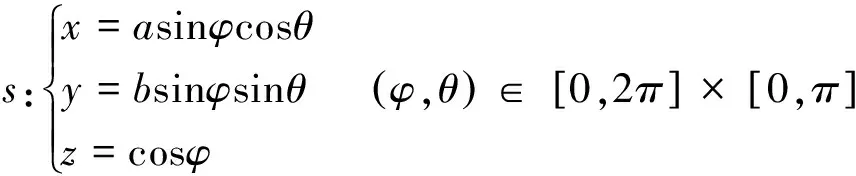
直接计算可得：

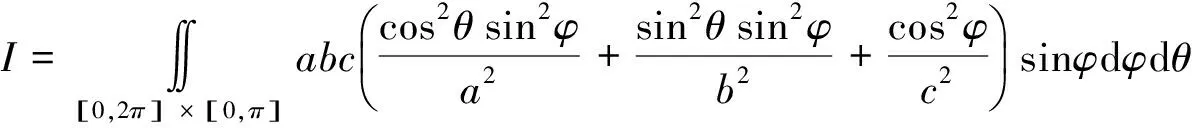
[1] Dold J W.An efficient surface-integral algorithm applied to unsteady gravity waves[J].Journal of Computational Physics,1992,103(1):90-115.

[2] 郭嗣琮,赵颖,韩建.基于结构元的模糊值函数曲面积分[J].数学的实践与认识,2017,47(12):239-244.

[3] 刘春凤,袁书娟.再谈积分学——宏积分[J].河北联合大学学报(自然科学版),2017,39(1):108-113.

[4] Wang Y.Simplifing the evaluation of the first type surface integral by element-method[J].Mathematical Theory & Applications,2010,42(5):224-236.

[5] 华东师范大学数学系.数学分析(下)[M].2版.北京:高等教育出版社,2000:303-304.

[6] TUCK E O.Some accurate solutions of the lifting surface integral equation[J].Journal of the Australian Mathematical Society,1993,35(2):127-144.

[7] 宁荣健,周江涛.曲面积分的换元法[J].大学数学,2017,33(2):73-78.

Calculation for the first Type Surface Integral in Parameter Equation

REN Yixiong1，XU Huai2

(1.School of Physics and Materials Science of Anhui University，Hefei Anhui 230039,China;2.School of Mathematics，Anhui University，Hefei Anhui 230039,China )

The first type surface integral is widely used.In this paper we present two proofs of the calculation formula when the surface is given by a parameter equation.One is using the method of vector projection method,the other is calculating area element of surface directly.Finally,we give two numerical example in the end of the article.

surface integral;double integral;parameter equation

2017-10-20

安徽高校自然科学研究重点项目(KJ2016A033)

任一雄(1997-),男,内蒙古乌兰察布人,2016级应用物理专业本科生,研究方向为理论物理。E-mail:b31614052@stu.ahu.edu.cn

徐怀，E-mail:Xuhai@ahu.edu.cn

O213.9

A

1004-2237(2017)06-0016-04

10.3969/j.issn.1004-2237.2017.06.004