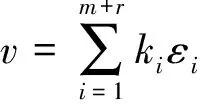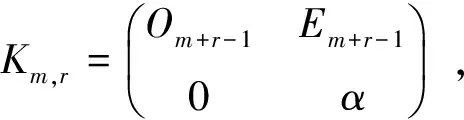循环半群及其矩阵表示
2017-12-22
(上饶师范学院 数学与计算机科学学院,江西上饶 334001)
循环半群及其矩阵表示
徐诚慷, 周彪, 石黄萍
(上饶师范学院 数学与计算机科学学院,江西上饶 334001)
循环群在群同构意义下只有两类,即整数加法群和整数模n剩余类群。证明了循环半群共有6类,其中无限循环半群有整数加法群、非负整数加法半群和正整数加法半群这三类,而有限循环半群也只有三类:整数模n剩余类群,还有两类变换半群。更进一步,对有限循环半群给出两个矩阵表示。
半群;循环半群;矩阵表示
1 循环半群的几个例子
在这一部分我们先给出半群的定义,以及6个互不同构的循环半群的例子。
定义1[1]设S是一个集合,在S上有一个二元运算。若该二元运算满足结合律,则称S为一个半群。若S含有单位元,则称为幺半群。与循环群类似,若S可由一个元素a生成,则称S为循环半群,记S=〈a〉。
对半群的研究主要集中在其结构方面。循环半群作为最简单的一类半群,在结构方面已有很多结论,例如文献[2-4]。在本文中当提到循环半群S时,我们都默认其有一个生成元为a。对一个循环半群S的阶S(元素个数)有如下的判定。
引理2S有限的充要条件是存在不同的非负整数k,l使得ak=al。
证明:设n=S有限,考虑S的子集{ak|k=1,2,…,n,n+1},它有n+1个元素,则其中必有两个是相等的。
反过来,若存在不同的非负整数k,l使得ak=al,则显然集合{k>0|存在l 下面我们给出6个循环半群的例子。 例1 整数加法群(Z,+)。群必是半群。 例2 非负整数加法半群(N,+)。 例3 正整数加法半群(Z+,+)。 很容易验证以上3个例子都是无限的循环半群。下面3个例子都是有限循环半群。 例4 整数模n剩余类群(Zn,+),这是一个n阶循环群。 例5 此例来自文献[5]。 对任意正整数m>1,r,记集合A={1,2,…,m,m+1,…,m+r},在A有一个变换σ定义如下: 用类似置换群中置换的表示方法,我们可记 则在集合A的变换半群中,由σ生成一个循环半群,记为〈σ〉。容易看出半群〈σ〉中没有单位元。在本文中符号σ均用以表示此例中集合A上的这一变换。 例6 对任意不含单位元的半群S,令S1=S∪{e},其中e与S中元素的乘法定义为 ea=ae=a,∀a∈S。 则S1构成一个幺半群。特别地,由例5中的半群〈σ〉,我们得到一个循环幺半群〈σ〉1,我们把这里添加的单位元(即集合A上的单位映射)记为1A。 下面我们给出循环幺半群〈σ〉1几个简单的性质。 证明:直接计算可知σm+r=σm,所以σm=σm+r=σrσm=σrσm+r=σm+2r。则由归纳法可得σm+rk=σm。 对s≥m,有σs+rk=σs-mσm+rk=σs-mσm=σs,证明了(1)。 当n σn=σm+kr+s=σsσm+rk=σsσm=σm+s∈〈σ〉1。 这同时证明了(2)(3)。 对任意am+s,am+t∈Kσ,存在正整数k使得s-t+kr≥m。则σs-t+kr∈Kσ,且 σm+tσs-t+kr=σm+s+kr=σm+s, 即方程σm+tx=σm+s在Kσ中有解。又Kσ是交换半群,所以Kσ是一个r阶群。注意到存在整数0≤g 下面我们给出本文的一个主要定理。 定理4 设S=〈a〉是一个循环半群,则S必然同构于例 (1)-(6) 中的某一个半群。 在这一部分我们就对定理分六种不同的情形给出证明。我们沿用上一部分的记号。 首先由引理2,当S=+时,不同的整数k对应的元素ak互不相等。 情形1S=+,有单位元,生成元可逆。此时显然S中所有元素可逆,即S是一个无限循环群,所以S同构于整数加法群(Z,+),同构映射为ρ1:akаk,k∈Z。 情形2S=+,有单位元,生成元不可逆。此时S中除单位元以外的所有元素都不可逆, S={ak|k=0,1,2,3,…} (k=0时为单位元)。 则显然映射ρ2:akаk,k≥0是从S到非负整数加法半群(N,+)的半群同构映射。 情形3S=+,没有单位元,此时S={ak|k=1,2,3,…},映射ρ3:akаk,k>0是从S到正整数加法半群(Z+,+)的半群同构映射。 无限循环半群在同构意义下只有(Z,+),(N,+),(Z+,+)。接下来我们讨论有限循环半群,即S<+。由引理2 可知,存在正整数k,l使得ak=al。因此集合{k>0|存在l>0使得ak=al}非空,记m为该集合的最小正整数。则集合{l>0|am+l=am}也非空,记其最小元素为r,即有am+r=am。这里的正整数m、r分别称为循环半群S的指数和周期。 类似命题3可证Aa={ak|k=1,2,…,m,m+1,…,m+r-1}是S的一个循环子半群,且它包含一个r阶循环子群{ak|k=m,m+1,…,m+r-1}。 情形4S<+,S=Aa,且m=1。此时有S=Aa={ak|k=1,2,…,r}为一个r阶循环群,因此S同构于整数模r剩余类群(Zr,+),同构映射为 情形5S<+,S=Aa,且m>1。此时S中没有单位元,所有元素互不相等。定义从S到例5给出的循环半群〈σ〉的映射如下: ρ5:akаσk,k=1,2,…,m+r-1。 显然ρ5是一个半群同构映射。 情形6S<+,S≠Aa。注意到SAa中元素必是ak,k≤0的形式。对任一元素a-k∈SAa,k≥0,有a0=a-kak∈SAa,即半群S中有单位元。更进一步,若有元素a-k∈SAa,k>0,则a-1=a-kak-1∈S,即S的生成元a可逆,则S为有限循环群,因而与情形4雷同。为免重复,我们可设S=Aa∪{a0}。此时S≃〈σ〉1,同构映射为 ρ5:akаσk,k=0,1,2,…,m+r-1(这里σ0=1A)。 至此,我们完成了定理4的证明。 在这一部分中,我们给出有限循环半群的两个矩阵表示,F表示一个特征0的域。我们只需对情形4、5进行讨论,而情形6的循环半群的矩阵表示可由情形5得到的矩阵表示添加相应的单位矩阵得到。由定理4,我们不妨设S=〈σ〉(注意到S的指数等于1即是情形4)。此时S=m+r-1,其中m、r分别为半群S的指数与周期。 我们给出的第一个表示的空间是m+r维的。设V是一个域F上的m+r维线性空间,有一组标准正交基ε1,ε2,…,εm+r。定义半群S在集合{ε1,ε2,…,εm+r}上的作用如下: σ(εi)=εσ(i),i=1,2,…,m+r。 φ1:S→EndV,σkаKm,rk,k=1,2,…,m,m+1,…,m+r-1。 显然这个表示来自半群EndV在V上的自然表示。 接下来我们再给出S一个在m+r+1维线性空间上的表示。设W是一个域F上的m+r+1维线性空间,有一组标准正交基ε1,ε2,…,εm+r,εm+r+1。记 φ2:σkаτk,k=1,2,…,m,m+1,…,m+r-1。 显然这是一个半群的单同态,同态像就是由矩阵Am,r生成的半群。即我们得到一个半群S在m+r+1维线性空间上的表示。而且从这个表示我们很容易看到,S的生成元σ(在同构意义下就是矩阵Am,r)是由一个m+1维线性空间上的幂零映射Nm+1和一个r维线性空间上的置换Pr合成的。 [1] 盛德成.抽象代数[M].北京:科学出版社,2000:23-27. [2] 项观捷.关于单演半群的周期和指数[J].山东师大学报(自然科学版),1994,9(4):18-20. [3] 赵雨清.单演半群的几条性质[J].湘潭师范学院(自然科学版),2004,26:20-22. [4] 徐文锋.有限单演半群的性质[J].韶关学院学报(自然科学版),2016,37(12):4-6. [5] HOWIE J M.Fundamentals of semigroup theory[M].Oxfold:Clarendon Press,1995:7-11. Monogenic Semigroups and their Matrix Presentations XU Chengkang,ZHOU Biao,SHI Huangping (School of Mathematics and Computer Science,Shangrao Normal University,Shangrao Jiangxi 334001,China) There are only two different isomorphic classes of cyclic groups,the group of integers and the group of integers modulo n. In this paper we prove that there are only 6 different classes of cyclic semigroups in the sense of isomorphism,of which the three infinite classes are the group of integers,the semigroup of non-negative integers and the semigroup of positive integers,the three finite classes are the group of integers modulo n,and two transformation semigroups. Moreover,two matrix presentations for the finite cyclic semigroups are given. semigroup;cyclic semigroup;matrix presentation 2017-06-02 数学天元基金项目(11656157);江西省教育厅科技项目(GJJ161044) 徐诚慷(1985- ),男,江西上饶人,讲师,博士,研究方向:代数学、李代数及其表示。E-mail:xiaoxiongxu@126.com O152.7 A 1004-2237(2017)06-0001-04 10.3969/j.issn.1004-2237.2017.06.001
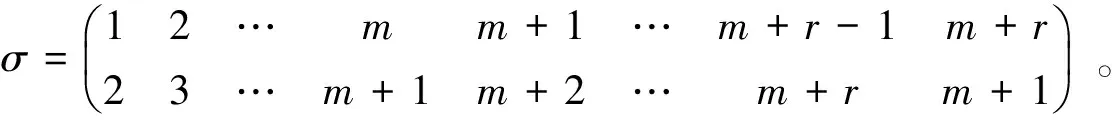
2 定理的证明
3 有限循环半群的矩阵表示