基于Spark框架的电力大数据清洗模型*

王冲，邹潇

（1.国网内蒙古东部电力有限公司信息通信分公司，呼和浩特010020；2.兰州大学 数学与统计学院，兰州730000）

0 引 言

电力大数据具有数量大、维度高，数据模式繁多等特征，在电力大数据的采集过程中，其不可避免的存在异常数据，对电力大数据清洗有很强的必要性［1］。国内外对电力大数据清洗研究主要有聚类和关联分析［2］、条件函数依赖［3］、马尔科夫模型［4］、DS证据理论［5］。大部分数据清洗技术都需要依赖数据模型本身构建异常数据识别规则，对检测到的异常数据做删除或均值填充处理，其缺点就是：破坏了数据的连续性、完整性、准确性。

针对以上电力大数据清洗难点，本文提出一种基于Spark框架的电力大数据清洗模型。相比一些电力大数据清洗模型，本文数据清洗模型减少人为干预，不需要根据数据关系模式设定识别规则，异常识别算法依赖于历史数据中的正常样本数据，且对异常数据修正是建立在其同一时间序列数据分析的基础上，最终能够实现对历史或实时数据中的异常数据清洗。

1 基于Spark框架的电力大数据清洗模型

电力大数据清洗是对检测到的电力大数据中异常数据进行修正的过程，利用Spark框架构建电力大数据清洗模型时分为以下几个阶段：数据准备、正常簇样本获取、异常数据识别、异常数据修正、修正数据存储。数据准备即将存储在传统关系型数据库中的数据转存在适合于大数据处理的非关系型数据库中，然后加载到Spark的弹性分布式数据集（RDD）中；通过抽取一定数量的电力大数据样本，应用层次聚类算法将其中的异常点抽取，获取可用于实现边界样本异常识别算法的正常样本簇；异常数据识别是建立在边界样本的基础上，通过边界样本异常识别算法完成对电力大数据中的异常数据检测；异常数据修正完成对检测到的电力大数据中的异常数据的修复。清洗步骤如下：

（1）数据准备：将数据存储在分布式文件系统HDFS中；

（2）从分布式文件系统上读取数据并执行cache操作生成RDDs，将数据读入到内存；

（3）利用改进的并行 CURE聚类算法获取正常簇；

（4）从正常簇中选取边界样本数据；

（5）设计基于边界样本的异常数据识别算法，并对测试样本识别异常数据；

（6）标记异常数据所在检测样本中的位置；

（7）对异常数据应用指数加权移动平均数进行修正；

（8）形成修正数据集并保存。

基于spark框架的电力大数据清洗模型框架如图1所示。

图1 基于spark框架的电力大数据清洗模型Fig.1 Data cleaning model for power big data based on Spark framework

本文接下来针对电力大数据清洗模型中的几个核心步骤进行分析。首先详细描述了改进CURE聚类算法获取正常簇；其次介绍了边界样本的选择过程，并对边界样本的异常数据识别算法进行了详细分析；最后阐述了指数加权移动平均数对异常数据进行修正。本文在最后给出了实验验证及分析，并对本文工作进行总结并指出进一步的研究方向。

2 正常簇样本获取算法

在对电力大数据进行异常识别时，由于电力大数据在采集过程中采集设备具有数据校验功能，因此采集的数据大多为正常数据，异常数据较少，同时电力大数据的种类繁多导致不能直接构建单一规则或设定阈值进行异常识别［9］。直接对采集上来的电力大数据进行异常识别计算量大且识别效率低。因此可以从电力大数据历史数据样本中获取正常样本簇，在正常簇的边界样本集的基础上对历史或实时电力大数据进行异常识别，这种异常识别不依赖数据属性阈值及属性数学模式规则，同时可提高检测的效率。

CURE聚类算法在对测试样本进行聚类时通过消除离群点降低对聚类结果的影响，可通过CURE聚类算法对测试样本进行聚类获取正常样本的聚类簇。CURE聚类算法分别在两个阶段对离群点进行删除：第一阶段是在聚类增长非常缓慢的类作为离群点删除；第二阶段是在聚类结束时将对象数据明显少的类作为离群点删除。但是通过CURE聚类算法对离群点进行删除时存在以下两个问题：

（1）很难对聚类过程中增长缓慢的类做界定，对这里离群点何时删除，如何界定增长缓慢［7］；

（2）对离群点删除后因局部数据的分布特征存在掩盖现象［8］。

针对CURE聚类算法剔除异常点时存在的问题，本文使用离群程度用于判定离群点，可有效解决增长缓慢的离群类难界定及局部离群点被淹没的现象。相关定义如下：

定义1：对每个划分的数据块进行聚类，得到的数据簇表示为pi（mpi，wi），其中pi表示块中第i个簇，表示为第i个簇的中心点，mpi表示每个中心点的权重值，wi是每个簇中数据的个数。因此每个划分的数据块可以使用若干个代表，pi称为代表点。

定义2：设代表点的集合为P，每个代表点pi的中心点到簇外任意一点的偏差距离表示为离群程：

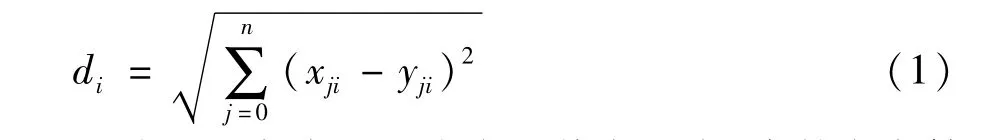
用欧氏距离表示一个点的偏离程度，当某点离簇中心点越远，则离群程度值越大。

定义3：设离群程度集为D，定义离群程度判定值为：

定义4：设离群参数为，离群程度最小值为：

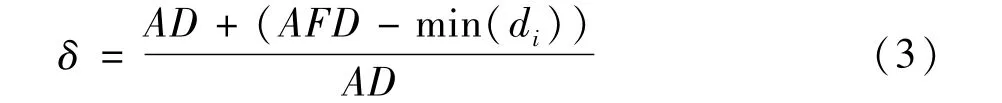
定义5：对于离群程度集D中任意，若，则所对应的代表点为离群点，其所在的簇中的数据即为离群数据。

算法基本思想是：首先从数据集中抽取一个随机样本，且样本的选择应该具有代表性；其次，将样本划分为若干个相同大小的数据集；对划分完成首次聚类，得到m/q各簇，然后计算簇中每个点的离群程度判定值（AD）及离群参数（δ）；删除不满足的离群点；然后对m/q个簇进行第二次聚类，同时删除簇中样本点明显少的类，最后将所有剩余的数据点指定到最近的簇，完成聚类，得到正常簇样本。

3 基于边界样本的异常数据识别算法

本文提出了基于边界样本的异常数据识别算法，首先通过获取正常簇的边界样本集；然后根据异常数据识别算法检测异常数据；最后标记异常数据并记录所在位置。异常数据识别是对电力大数据中历史或实时流数据中的异常数据检测的过程，是建立在正常簇的边界样本的基础上。每个正常簇的边界样本必须具有以下特点：（1）距离质心最远；（2）分散在正常样本的四周；（3）能够代表正常样本的形状。

对于正常簇样本如何保证其选择的边界样本点能够分散在正常簇样本的四周，符合边界样本分布特点，下面给出其相关数学证明。

证明1：在一个三角形中，位于底边中垂线上的顶点使得到其底边两点距离之和最短，且周长最短。图2给出了三角形顶点在中垂线上和不在中垂线上的情况。

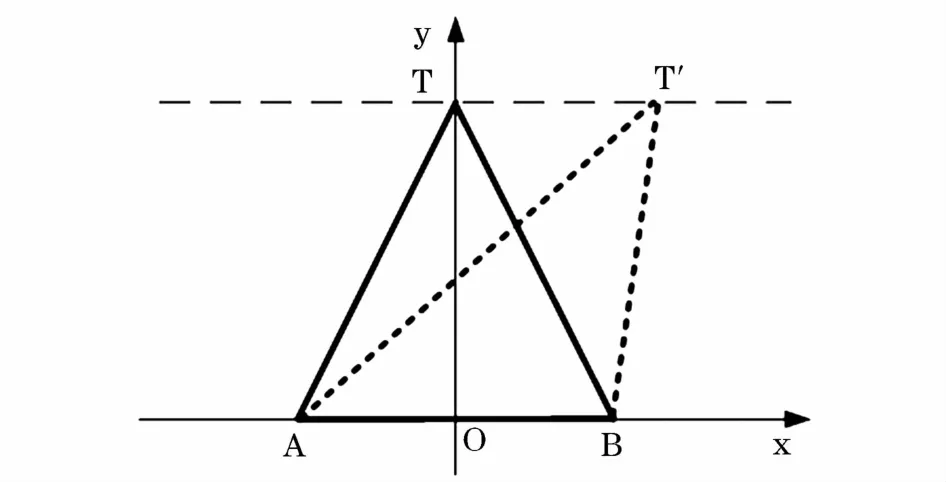
图2 三角形顶点分布Fig.2 Triangle vertex distribution

在三角形TAB中，高为b，底边|AB|=2a，顶点坐标为T（x，b），现在需要证明位于中垂线上的顶点T使得|TA|+|TB|值最小。根据公式可得：

公式两边求导数可得：

通过对公式求极值，当x=0时，可以得到distance（|TA|+|TB|）取得极小值，。

证明2：椭圆上一点M使得到椭圆上其他两点C和B距离之和最大。

图3给出了椭圆形数据节点的分布示意。

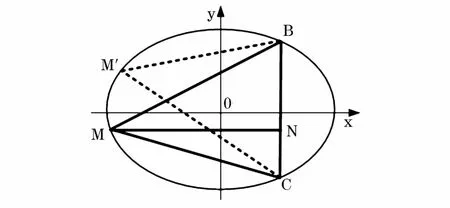
图3 椭圆型数据点分布Fig.3 Elliptic data point distribution

长轴长为2m，短轴长为2n，|BC|=2a，设MN为距离BC最远点所在的直线，|MN|=b，假设M｀为距离边BC两个短点距离之和最大的点，根据证明可以得出。

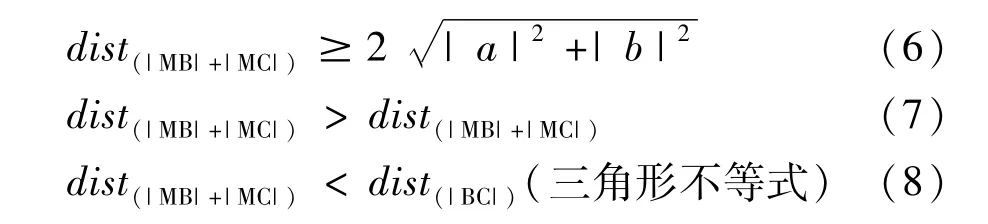
通过式（7）可以看出M｀不会出现在B、C半径为周围。因此如果选择B、C作为代表点，M｀也可以作为代表点，使得M｀、B、C作为代表点足够分散。

在对边界样本点进行选择时，应保持边界样本点的特点，下面给出边界样本的选择过程：

步骤1：计算簇的中心点，m为簇的点个数；

步骤2：第一个边界样本点为离中心点最远的点，第二个边界样本点为离第一样本点最远的点，i为最大点距离下标，j第二个样本点下标；

步骤3：接下来选择的边界样本为离前两个样本点距离之和最大的点，直到选取的样本点能够代表聚类簇，则选择停止。

正常簇的边界样本选择过程如图4所示。

式（4）～式（6）经过加减处理后可得：

图4 正常样本簇的边界样本选择过程Fig.4 Selection process of border cluster sample of normal sample

设正常簇样本的边界样本集为B=｛b1，b2，…，bn｝，正常簇样本的边界样本集的获取已在上文提及，正常簇样本的识别半径为rs。待测试样本为T=｛t1，t2，…，tm｝，该测试样本可为信息机房监测数据历史样本或信息机房实时监测数据。S为识别出的非异常监测信息，N为识别出的异常监测信息。

以边界样本集作为平面检测器，异常信息识别规则表示为：

式中l1为待识别样本点到边界样本的距离序列最小值；l2为待识别样本到边界样本距离最远点距离值；dm为待识别样本到质心距离；r为正常簇样本的识别半径。

边界样本点分散在聚类簇的四周，能够表示聚类簇的形状。利用正常簇的边界样本来识别待检测样本，可以减少异常识别算法的计算量。针对异常信息识别规则，基于边界样本的异常识别算法的具体实现步骤如下：

算法输入：待识别样本T=｛ti，i∈［1，m］，m为待识别样本总数｝，边界样本集B=｛bj，j∈［1，n］，n为边界样本总数｝，正常簇样本ki的质心m；

算法输出：异常数据信息Q；

步骤1：计算待识别样本点ti到边界样本点bj的距离，构成距离序列dist，dist=｛d1，d2，…，dn｝；

步骤2：计算正常簇样本的识别半径rs；

步骤3：查找距离序列dist中最小值l1=min（di）；

步骤4：在边界样本里查找与待识别样本点ti距离最远点bk，计算ti到bk距离l2=distance（ti，bk）；

步骤5：如果l1＞=l2，则待识别样本点ti为异常数据；若l1＜l2，则执行步骤6；

步骤6：计算ti到正常簇样本ki的质心m的距离，dim=distance（ti，m）；

步骤7：如果dim＞rs，则待识别样本点ti为异常数据；若dim＜=rs，则待识别样本点ti为正常数据；

步骤8：标记异常数据所在样本中的位置，并将信息进行反馈；

步骤9：重复执行步骤1～步骤8，直到所有待识别样本都识别完毕；

步骤10：输出所有异常信息，并做下一步处理。

通过边界样本异常识别算法，在进行异常识别时，不必设置异常识别的阈值，同时可以避免因使用数据模式带来的复杂性，可以提高异常识别的效率。

4 基于时间序列分析异常数据修正

电力大数据是在一定时间周期内采集的数据的积累，电力大数据因其种类多，随时间变化一般呈现三种规律：周期变化型数据、幅值变化较小型数据、缓慢增加型数据［10］。

对异常数据进行修正时要根据异常数据所在数据区间数据特点及异常数据表现形式，对不同类型的异常数据进行分析修正。对缓慢增加或衰减型电力大数据中的异常数据进行修正时，选取的参考数据序列为异常数据所在序列的［n，m］区间；对周期性变化型电力大数据中的异常数据进行修正时，选取的数据序列为包含异常数据在内的n个周期内的异常数据所在的时刻t的数据序列。

在对异常数据进行修正时，一般采用的方法是使用该异常数据所在序列的平均数进行代替。这时修正的值为，式中xi是对给定的一个权值。但是，某一序列值对后面序列值的影响作用是衰减的，而不是一直是。因此对异常数据进行修正采用指数加权移动平均数：

5 实验及结果分析

本文采用“Spark On Yarn”集群模式构建电力大数据清洗模型实验环境，实验采用6台服务器组成数据清洗集群节点，其中一个节点为Master，其余五个节点分别为 Slave1-Slave5，每个节点的配置见表2。每个服务器节点采用Ubuntu-12.04.1操作系统，使用 Hadoop-2.6.0，Spark-1.3.1，Scala-2.10.5，JDK-1.7.0_79搭建节点的软件环境。实验平台在Scala的Intellij Idea开发环境上进行开发实现，以hadoop的hdfs实现数据结果的存储。

以某风电场风力发电监测数据作为数据清洗研究对象。该风力发电监测数据大小为5 GB，分别从5台风力发电机采集，采集间隔为1 s，记录了从2012年2月1日到2012年2月29日风力发电监测数据。

集群配置具体如下：

服务器类型：刀片型。服务器数量：6。

内存：6×128 GB。CPU核数：6×16。

网卡速率：1 Gbit/s。硬盘容量：6×1 T。

处理器类型：Intel Xeon 2.00 GHz。

本文将从异常识别的准确性、异常修正的效率对电力大数据清洗模型进行验证分析。

实验1：针对正常样本获取过程中离群点删除算法，本文测试了几种离群点检测算法的检测率和误检率，测试结果见表1。与Apriori算法相比，本文算法在检测率相似的情况下，误检率较低。

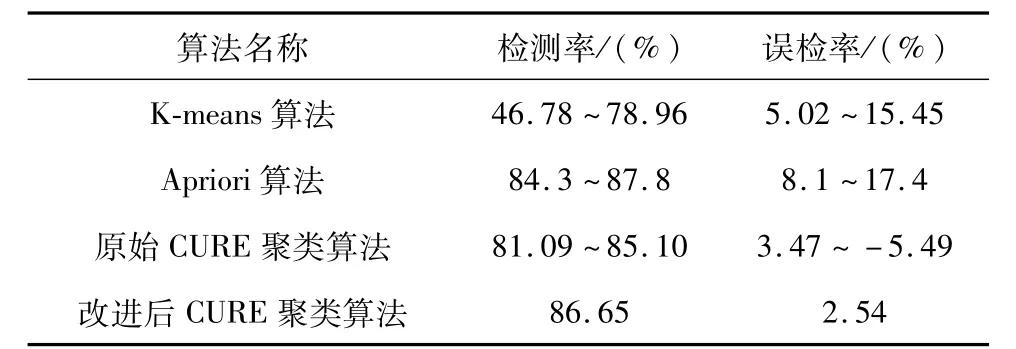
表1 离群点检测算法比较Tab.1 Comparison of outlier detection algorithms

实验2：为了验证电力大数据异常识别算法的检测异常数据正确性，实验保持集群节点数固定，不断调整测试数据样本大小，检测算法的准确率，结果如表2所示。模型检测到了大部分的异常数据。

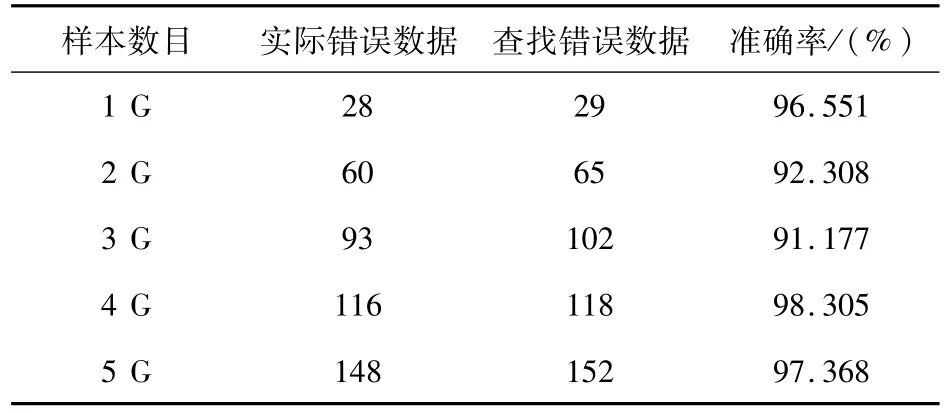
表2 电力大数据异常识别算法的准确率测试Tab.2 Accuracy test of power big data anomaly identification algorithm

实验3：为了验证电力大数据清洗模型的高效性，测试了传统单机数据清洗与基于Spark框架的电力大数据清洗模型不同数量的清洗所需要的时间。集群节点数固定，不断调整待清洗数据样本大小，测试数据清洗时间，测试结果见表3。

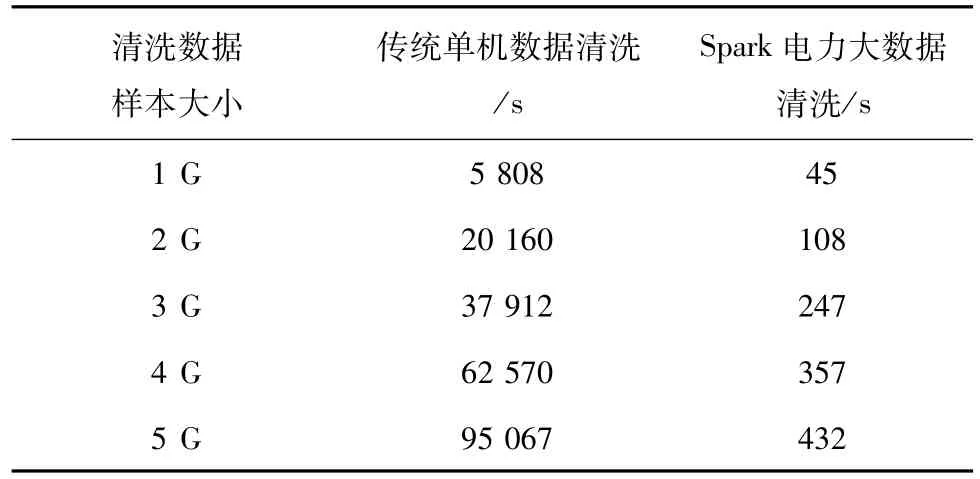
表3 单机及并行数据清洗清洗时间比较Tab.3 Cleaning time comparison of single with parallel data cleaning

实验4：固定测试数据样本大小，从中随机抽取15 000条数据作为实验测试样本，正常簇样本个数为5，每个正常样本簇的边界样本个数分别为25，35，45，55，65，在待识别样本数目固定的情况下，对上述测试样本采用基于边界样本的异常信息识别方法进行异常信息识别，检测正常样本簇的边界样本个数对检测结果的影响，结果如表4所示。

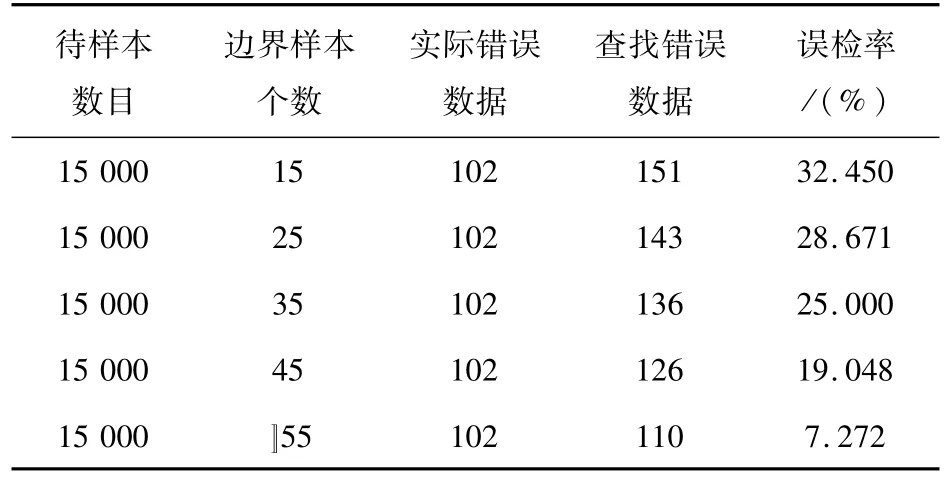
表4 基于边界样本的异常信息识别方法实验结果Tab.4 Experimental results of information identifying based on abnormal samples boundaries

6 结束语

本文分析了电力大数据清洗过程中的若干难点，并针对电力大数据的特点及清洗难点提出了基于Spark框架的电力大数据清洗模型。该清洗模型具有以下特点：

（1）异常数据识别无须外源数据；

（2）异常数据识别及修正准确性高；

（3）利用并行Spark大数据处理框架，具有高效性。但是，本文在选取正常簇的边界样本时仍然存在问题，即何时达到最优边界样本数；其次，对异常数据的修正是建立在同一时间序列的样本上，若该时间序列出现异常对异常数据修正的准确性仍会有影响。针对以上解决问题需要在以后的工作中进一步探讨优化并完善电力大数据清洗模型。