多谐波源的谐波电流耦合及解耦策略研究*
2017-12-21江友华常建唐忠
江友华,常建,唐忠
(上海电力学院电子与信息工程学院,上海200090)
0 引 言
随着配电网内越来越多的非线性装置或分布式电源的使用,谐波源相互之间的影响也越来越强,谐波源之间的耦合变得越来越不容忽视。谐波耦合将使谐波责任区分变得模糊,影响用户责任的定量分析,使谐波治理中的滤波器协调控制变得困难,同时电网中谐波电流的叠加、抵消可能导致谐波放大甚至谐振的产生。由此可知,面对电网中谐波源电压等级不同、类型各异、分布面广等构成的多目标、非线性强耦合状况,如何实现它们之间的解耦,使得多谐波源的责任区分、谐波源定位及治理能够像单个谐波接入点一样物理清晰,将是多谐波源宏观研究所面临的挑战。国内外针对多谐波源系统解耦策略也有相应的研究。文献[1]出于工程实践的考虑,忽略了基波潮流与谐波潮流的相互影响,对每个方程进行独立迭代,实现谐波与基波潮流的解耦。文献[2-3]针对系统与谐波源的相互影响,提出迭代分析法求解系统方程和非线性方程。文献[4]提出的解耦法,考虑了基波、谐波对各节点的注入电流的影响,计算精度高。但这种方法计算量较大,占用内存较多。文献[5]中运用完全解耦的方法,虽然此算法具有速度快,收敛性能好,程序设计简单的特点,但是它没有考虑到在基波迭代的过程中谐波对其的影响,具有精度不高的问题。
为此本文提出一种基于奇异值分解理论(SVD)的解耦算法,该解耦算法极大的降低了计算量,尤其是在数据矩阵维数较高时优势明显,大大提高了计算的准确性和有效性,然后通过MATLAB/SIMULINK仿真分析计算,筛选出谐波耦合特性强的节点,用于指导谐波治理装置的优化配置,为多谐波源的责任区分、谐波源定位提供清晰的思路。
1 多谐波源的耦合模型
电网是多个谐波源并存的复杂网络,因此对其进行谐波分析,就不能仅限于单个谐波源建立模型,需要建立起整个谐波源网络的模型[6]。谐波源网络中各个节点的连接状况可用导纳矩阵来反映。
谐波源的计算是谐波网络方程与谐波源特性方程在数学上的结合。考虑谐波源基波与高次谐波的影响,以及不同谐波源不同频率谐波电流的影响,对应的谐波网络节点方程如下:
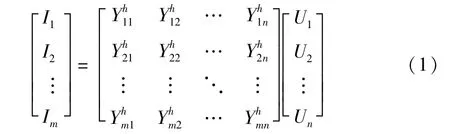
其中Ik=[Ik,1Ik,3Ik,5…]T(k=1,2,…,m),表示第k个谐波源的基波电流与各奇次谐波电流,是个列向量;(i=1,2,…,m,j=1,2,…n),即第i个谐波源的h次谐波电流与第j个谐波源的各次谐波节点电压的导纳向量,是个常量;Uk=[Uk,1Uk,3Uk,5…]T(k=1,2,…,n),即第k个谐波源的基波电压与各奇次谐波电压。以I3即第3个谐波源的谐波电流为例,假设有5个谐波节点电压:

式(2)表示第3个谐波源的基波电流与各奇次谐波电流;式(3)表示每个节点各次电压对第3个谐波源各次电流的影响大小;式(4)表示每个节点的基波电压和各奇次谐波电压。
以上公式可简写为:

式(5)就是本文提出的谐波耦合矩阵模型,Ih为谐波电流注入向量;Uh为谐波节点电压向量;Yh称为谐波耦合导纳矩阵,其中矩阵元素的物理意义如上所述。基波电压对谐波电流的影响比谐波电压的影响要小的多。该模型适用范围广,能体现出各个谐波源电压和电流之间的耦合关系。
2 多谐波源系统的耦合因子分析
2.1 输电线谐波传导分析
上级电网主要通过输电线路对下级电网产生谐波耦合。为了方便分析,采用π型电路等效输电线,如图1输电线路所示的输电线等值电路,其线路阻抗可表示如下:

图1 输电线路等值电路Fig.1 Equivalent circuit of transmission line

式中ZCh、γh分别为对应于h次谐波的线路特征阻抗和传播常数,均为复数;l为线路长度,则对应于其h次谐波,有如下电路方程:

式中Uoh,Ioh分别为线路始、末端h次谐波电压和电流。若在电路始端有h次谐波电流源Iih,经线路传输l距离后流入电路末端的h次谐波电流源Iih,因此可得输电线路谐波传递系数为:
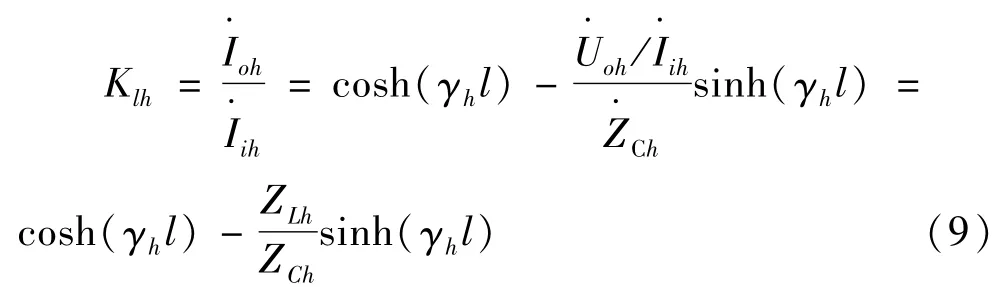
式中Zlh为对应h次谐波的传输线路阻抗。
由式(6)可以看出,随着谐波次数和线路距离的增大,城市高压电网谐波传递系数的阻抗和导纳与输电线路传递系数将发生变化,使得输电线路的谐波传导与耦合效应已不能被忽略。
2.2 耦合因子分析
针对多谐波源的耦合因子[7]求解问题,本文采用谐波源的戴维南等效电路,如图2所示。

图2 多谐波源戴维南等效电路Fig.2 Th even in equivalent circuit of multiple harmonic sources
以下公式推导均省略上标h,表示在h次谐波下进行。当供电侧谐波源单独作用时,在PCC处产生的谐波电压为:



Ick为谐波源Uck单独作用下支路的电流,在此,称为“理论电流”。那么,得出供电侧谐波源和用户侧谐波源分别单独作用下的谐波电压后,由叠加定理,就可以得到PCC处的谐波电压,即:

由此,得出支路中的某一谐波对PCC处的谐波贡献量为:
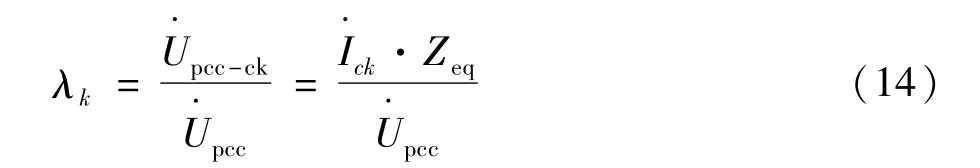
同样方法,可计算出谐波源Ucj单独作用下的相关参数:为除Zcj外,其他阻抗的并联阻抗。

Icj为谐波源Ucj单独作用下支路的电流。由此,可推断出谐波源Uck单独作用下支路的“实际电流”:

从而更改 λk为 λkj,即:

由此公式即可看出,在其他谐波源的影响下,该谐波源对PCC处谐波电压的贡献量,发生了明显的变化,即谐波之间产生了耦合。定义耦合因子:

此时计算的ω是谐波源j对谐波源k的影响大小,下面计算在所有谐波源同时存在的情况下,各谐波源对某个谐波源影响因子的大小。

此处 Vλk=λk-λ′k,λk为由谐波源发射出的谐波电流作用的指标因子,λ′k为其他所有谐波源加入之后的指标因子,ωi为式(18)计算的某一个ω,即两两之间的耦合因子,那么ζi就是要计算的综合指标耦合因子。各次谐波下的公式组合如下:

简写成:

用偏最小二乘法估计得:

3 基于奇异值分解的多谐波源系统解耦
3.1 SVD的基本理论知识
奇异值分解法是正规矩阵酉对角化的延伸,在解决最优化、最小二乘法以及多元统计分析等应用领域有着广泛地应用[8]。在统计学中的应用为主成分分析,用来找出大量数据中所隐含的模式。
非奇异矩阵A的SVD分解形式为:

矩阵U、D、V将在下面做详细介绍。
其优点是正交矩阵参与计算不放大误差,且正交矩阵求逆很方便,因此本文将采用该方法对多谐波源进行降维从而实现解耦。
设A为m×n阶矩阵,秩为r,则存在m阶正交矩阵U,其列由AAT的特征向量组成,n阶正交矩阵V,其列由ATA的特征向量组成,使得式(23)成立。其中,。特征值λ1≥λ2≥…λr>0是矩阵ATA的非零特征值的全体,而(i=1,2,…,r),称 σi(i=1,2,…,r)为A的奇异值,而式(23)称为A的奇异值分解式。记U=(u1,u2,…,um)、V=(v1,v2,…,vn),式(23)可写成:

式中O表示分块矩阵,元素为0。将式(23)进行变换如下:

矩阵A能够进行SVD分解的必要条件是:
当m>n时,式(25)可写为:

当m=n时,式(25)可写为:

当m<n时,式(25)可写为:

由式(26)~式(28)可以得到:

由式(29)可得:

U、V的构造方式如下:

构造V=(v1,v2,…,vn),V为n×n的正交阵,若:

显然,(u1,u2,…,ur)为ATA的特征值(i=1,2,…,r)所对应的特征向量。在m阶空间域中,补充向量ur+1,ur+2,…,um,使得(u1,u2,…,um)为m阶空间域中的一个规范正交基,再令U=(u1,u2,…,ur,…,um)为m阶空间域中的一个正交矩阵,则由式(31)和式(32)可得:

从上面的讨论可知,矩阵A总可以分解为式(23)所示的形式。
用SVD分解法求解线性方程组Ax=B,设A为m×n阶矩阵,x为n×n阶矩阵,B为m×m阶矩阵。再设U=(U1,U2)、V=(V1,V2),其中U1为U中前r列正交向量组构成的m×r阶矩阵,V1为V中前r列正交向量组构成的n×r阶矩阵。定义矩阵A的广义逆矩阵为:

那么方程组Ax=B的解为:

当m>n时,Ax=B为超定方程,将最小二乘法理论运用在SVD分解法中,由式(35)得:

当m=n时,若矩阵A的秩Rank(A)=n,则方程有唯一解,由式(35)可得结果依然是式(36)所示;若矩阵A的秩与其增广矩阵的秩相同,Rank(A)=Rank(A|B)=r(r<n),则等式有无穷解,通过式(35)求出一个特解x*与矩阵A零空间列向量的线性组合,即:

式中vj∈V2(j=r+1,r+2,…,n),所对应的σj=0(j=r+1,r+2,…,n);若矩阵A的秩与其增广矩阵的秩不相同,则方程无解。
当m<n时,若Rank(A)=Rank(A|B)=r,则方程有无穷解,形式如同式(37);若Rank(A)≠Rank(A|B),则方程无解。
3.2 多谐波源解耦算法
谐波源解耦,在理论上表现为将耦合矩阵转化为对角矩阵[9],使谐波源之间不再相互影响、相互干预;在实际中表现为对系统参数的修改,主要是导纳矩阵模型的修改,通用的方式是通过加滤波器实现,由式(18)可知,ωkj与其他谐波源电流、系统参数有关系,在某种程度上,可以认为式(21)中的F矩阵元素即Vλk也是由上述两项决定的。假设,各谐波源对第k个谐波源的影响如公式(22)所示,由式(22)得:
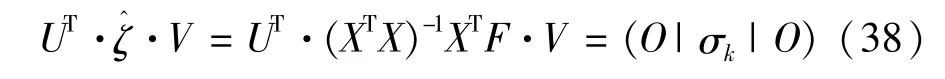
因为是对列向量的计算,因此等式中取D矩阵的第k行。
假设存在某种关系:

其中=[k1,k2,…,kn],表示第i(i=1,2,…,n,且i≠k)个谐波源与第k个谐波源之间的互阻抗,I=[I1,I2,…,In]T,表示各个谐波源的电流值,F表示在(n-1)个谐波源作用下第k个谐波源处的谐波电压值,则:
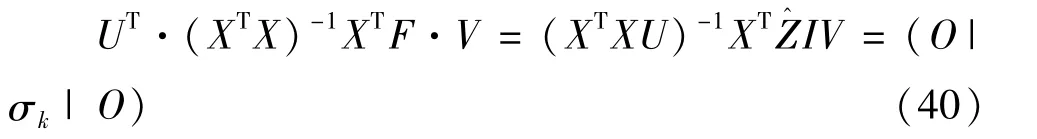
由此,便可求出矩阵的元素,中每一行对应的都可以用此种方法求出。公式(40)若成立,那么矩阵是满足式(40)。在理论上,将耦合因子向量转化成了对角向量,解除了谐波源之间的干扰。实际中,需要安置滤波器,那么滤波器的参数为:

其中[Zk1,Zk2,…,Zkn]由式(5)中Yh求逆得来。同样方法,计算耦合因子矩阵的每一行,使得耦合矩阵被完全解耦。
4 谐波传递案例及谐波耦合仿真分析

图3 上海泗泾分区下某辐射型子网示意图Fig.3 Schematic diagram of a radiation type sub-network in Shanghai Sijing partition
本案例以上海泗泾分区下的219 kV小环网为例,其示意图如图3所示,利用上海市电能质量监测系统实测数据来分析不同变电站之间的谐波影响系数的取值。由图3可知,该219 kV小环网共有9座219 kV变电站,包括500 kV泗泾站的219 kV母线,共有10条219 kV母线。
4.1 谐波传导对谐波电流耦合影响仿真分析
本数据是在泗泾站的500 kV母线上分别加上2次至2次单位谐波源,分析谐波电压由泗泾站500 kV母线沿着辐射型网络向低电压等级母线的传递情况,从而得出泗泾站对小环网其他母线的影响系数及谐波传递系统的计算结果。
由图4明显可以看出,同等变压等级,但随着站与站之间的电气距离不同,其传递系数有所不同,即传递系数Kh和站与站之间的电气距离有关,这同电网所建立的等值电路得到的传递系数式(9)相符合,也符合直观理解,电气距离近的两个站,谐波更容易相互传递。由图4还可以看出,传递系数Kh和谐波次数有关,谐波次数越高,站间影响系数越小;谐波次数越低,站间影响系数越大,影响系数随着谐波次数的升高而降低。由此可以看出,相对于低次谐波而言,高次谐波更容易衰减。
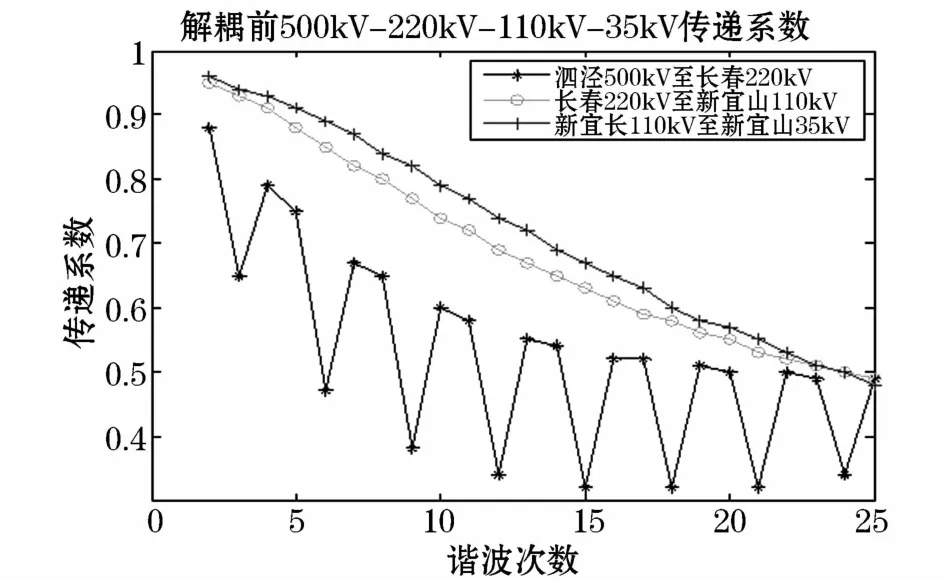
图4 解耦前500 kV母线至35 kV母线的传递系数Fig.4 Transfer coefficient from 500 kV bus to 35 kV bus before decoupling
图5是解耦前后传递系数的对比图,虚线表示解耦前的传递系数,实线为解耦后的传递系数,由对比看出,解耦后,传递系数减小。传递系数与电气距离和谐波次数有很大关系。解耦之后,传递系数有所降低,即传输线路上级对下级的影响程度变小。有利于改善因谐振引起的谐波放大现象,使得下级线路及设备电压浮动变小,减少了线路损耗。
4.2 多谐波源的耦合因子仿真分析
本文采用IEEE13节点模型进行仿真,该系统有2台发电机组、7个PQ节点、13条母线、12条支路和7台变压器组成。令Bus3作为关注母线X,母线8、10、13接谐波源负荷,其中母线8接牵引机车的牵引变电站,母线10接分布式发电电源,如整流器、调频器等电力电子设备,母线13为工业用电中的电 弧炉。图6为IEEE 13节点示意图,三谐波源共同作用时PCC处电流如图7所示。

图5 解耦前后500 kV母线至35 kV母线的传递系数Fig.5 Transfer coefficient from 500 kV bus to 35 kV bus before and after decoupling
谐波源8、10、13在Bus3处共同作用后的波形见图7。
利用2章节的公式计算出耦合因子ξ。结果如表1所示。
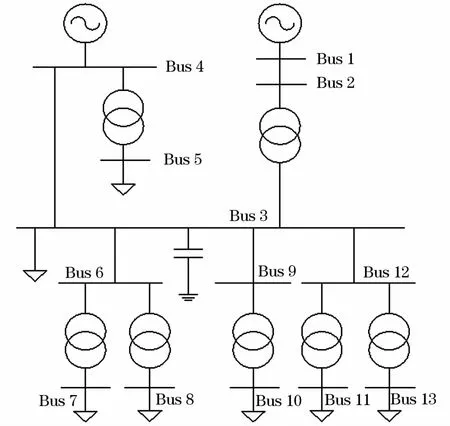
图6 IEEE 13节点示意图Fig.6 Schematic diagram of IEEE 13 node
表1表明,谐波源8和谐波源10之间的影响比谐波源10和谐波源13的影响作用大的多。因谐波源8与谐波源13之间的电气距离较远,计算出来的结果趋于零,这与实践经验相符合。因此,有必要对谐波源8、10进行解耦,以保证它们对Bus3的责任区分的相对独立。
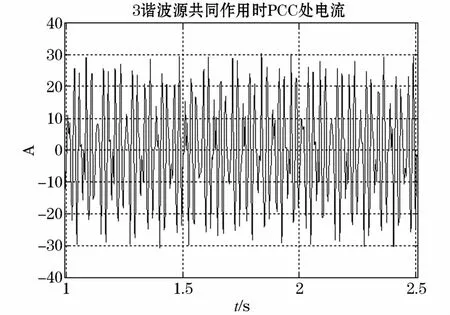
图7 三谐波源共同作用时PCC处电流Fig.7 Effect of three common harmonic sources at PCC current
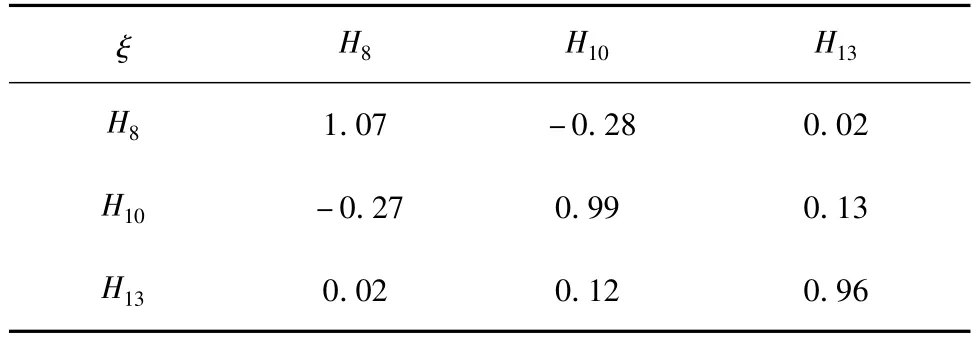
表1 多谐波源系统耦合因子Tab.1 Coupling factor of multi harmonic sources system
4.3 解耦前后的责任区分对比
支路中的谐波电流并非谐波源发射的电流,而是各谐波电流叠加的结果。用支路中的谐波电流计算谐波责任[10],不能代表用户应当承担的责任。谐波源发射的谐波电流在关注母线处引起的谐波电压,所占母线总谐波电压的比例是真实的责任大小[11]。
通用谐波责任公式如下:

首先计算考虑谐波耦合时,即正常运行下电网中谐波源的责任区分。利用公式(42)计算谐波源8、10、13对关注母线的谐波责任如表2所示。
由表2可以看出,谐波源8的谐波责任在5、7次谐波下为负数,是因为在关注母线3处,谐波源8产生的谐波电压与谐波源10、13产生的谐波电压相位相反,即削弱了谐波源10、13对关注母线电压的影响。

表2 解耦前谐波责任区分Tab.2 Harmonic responsibility partitioning before decoupling
如在5次谐波下,谐波源8的谐波责任为负值,此非线性负荷吸收了一部分谐波功率,抑制了谐波畸变。仿真结果表明谐波源13比谐波源8、10承担的责任多,说明对于关注母线3来说,谐波源13是主要的谐波源,而谐波源8、10是次要的谐波源。因此,在实施奖惩机制时,应当对谐波源13加大惩罚力度,而对于谐波源8可以实行奖励的策略[12]。
接下来根据第三节所述的解耦理论,解耦后的网络参数发生变化。鉴于此,责任区分也将发生变化。下面给出解耦后的谐波责任区分结果:
以5次谐波为例,由表3可以看出,负荷8在解耦前的责任大小为-8.84,与精确值-18.34比相差较大,而将谐波源解耦后,责任大小变为-17.10,与精确值更加接近。再比如13次谐波下,负荷13的责任由解耦前的66.74将为解耦后的64.72,与精确值的差值变小,这说明通过本文的解耦理论,使得谐波源与谐波源之间的耦合关系得到减弱或者解除,谐波源之间的干扰减小,因此责任区分的大小更加接近精确值。
为了更直观形象的对比解耦前后责任区分的效果,下面做出柱形图进行比较。将精确值、解耦前后的数值画在同一图形中,如图8~图11所示。
从上图可以直观看出不同次谐波下,解耦前后谐波责任的数值大小。解耦后,责任区分的数值进一步接近精确值,使责任区分更加准确公平,体现出奇异值分解理论的有效性和实用性。

表3 解耦后谐波责任区分Tab.3 Harmonic responsibility partitioning after decoupling

图8 5次谐波下责任区分Fig.8 Responsibility partitioning at the 5th harmonic
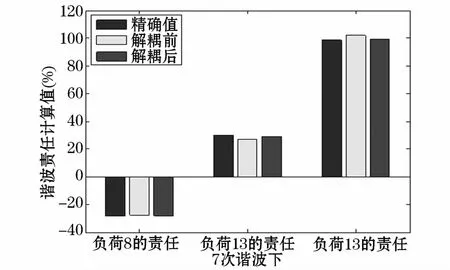
图9 7次谐波下责任区分Fig.9 Responsibility partitioning at the 7th harmonic
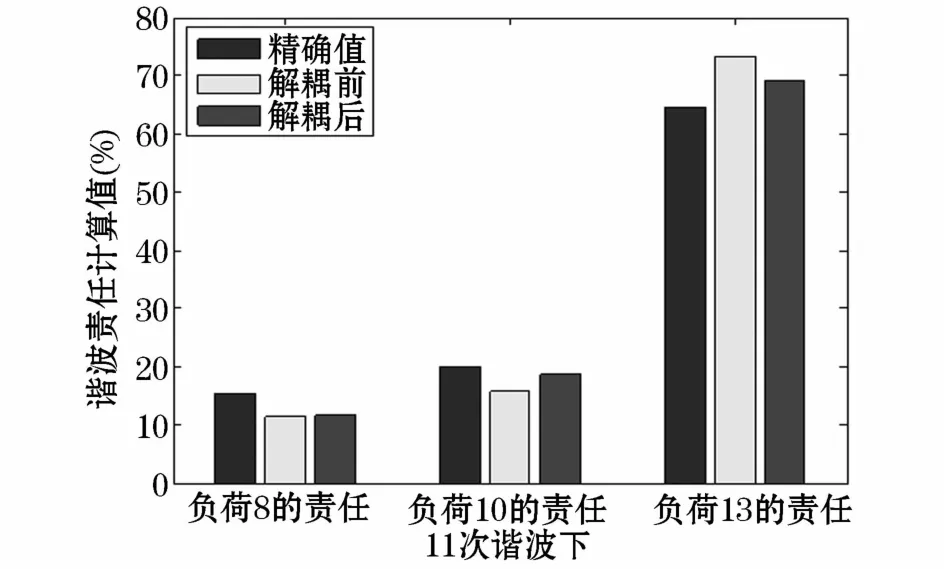
图10 11次谐波下责任区分Fig.10 Responsibility partitioning at the 11th harmonic
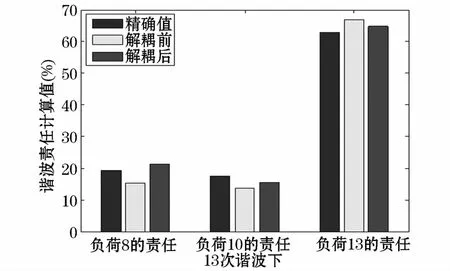
图11 13次谐波下责任区分Fig.11 Responsibility partitioning at the 13th harmonic
5 结束语
(1)提出一种基于奇异值分解理论(SVD)的解耦算法,核心思想是将待分解矩阵转换成三个矩阵的乘积,将耦合矩阵转变成对角矩阵,实现理论上的解耦;
(2)通过谐波传导实例仿真分析,解耦之后,传递系数有所降低,即传输线路上级对下级的影响程度变小。有利于改善因谐振引起的谐波放大现象,使得下级线路及设备电压浮动变小,减少了线路损耗;
(3)采用IEEE 13节点模型,设定不同谐波源位置,得出谐波源8、10之间存在强耦合关系,需要采取必要的解耦措施。结合解耦理论在责任区分中的应用,同样在IEEE 13节点中进行,对比解耦前后谐波责任大小,可以得出解耦后的值更加接近精确值,验证了理论的正确性和可行性。
