一种改进型扰动观察法在最大功率点跟踪中的应用
2017-12-21于子捷魏晨曦田芳芳胡骢耿乙文
于子捷,魏晨曦,田芳芳,胡骢,耿乙文
(中国矿业大学 信息与电气工程学院,江苏 徐州 221008)
0 引 言
为了解决传统能源带来的环境污染和能源短缺等问题,新能源的研究备受瞩目,而其中的光伏发电技术发展迅速[1-2]。光伏电池特性为非线性,输出特性受环境影响很大,为了降低发电成本,提高系统效率[3],需要采用最大功率点跟踪(Maximum Power Point Tracking,MPPT)技术[4],即控制光伏电池始终工作在最大功率点处。
目前最常用的最大功率点跟踪算法有三种:恒定电压法(Constant Voltage Tracking)、扰动观察法(Perturbation and Observation)和电导增量法(Incremental Conductance)[5]。恒定电压法的控制思想为光伏电池在温度变化不大的情况下,不同的光照强度下的最大功率点处的电压(Um)变化范围并不大,把MPPT控制简化为稳压控制,近似的实现MPPT[6-7];扰动观察法在每个控制周期对光伏阵列的工作电压施加一个小的扰动,比较扰动前后输出功率的大小,调节扰动方向,最终使光伏电池工作在最大功率点处;电导增量法通过不断比较光伏阵列的电导增量和瞬间电导来改变控制信号,使其达到最大功率点[8]。
传统扰动观察法在稳态状况下,其固定的扰动步长会在最大功率点附近引起震荡,并且当外界环境发生快速变化时还会出现误判断的现象。针对上述问题,学者们提出了众多改进方案[9]。
很多学者提出将扰动观察法与其他算法相结合来追踪最大功率点。文献[10]提出一种与模糊控制算法相结合的扰动观察法,文中Ovalle等人设计的模糊控制器的输入为功率PPV,电压VPV和P-U曲线的斜率dPPV/dUPV,其中用二进制变量来表示PPV和UPV,来表明当电池输出电压大于开路电压时的情况。与模糊控制算法相结合的扰动观察法有较好的动稳态特性,且可在光伏阵列局部遮光的条件下追踪到真正的最大功率点,但实现起来比较复杂,故在应用上受到了一定程度的限制。文献[11]提出与短路电流法相结合的变步长扰动观察法,该方法在外界环境突变时,采用改进的短路电流法初步跟踪到最大功率点附近,然后再采用双阶段变步长扰动观察法,将工作点进一步调节到最大功率点,这可以有效减少了工作点在最大功率点处的振荡,但该方法计算量大,并且要用到多个传感器,故导致成本较高[12]。文献[13]提出与开路电压法结合的扰动观察法,首先通过比较峰值电压Umpp与开路电压Uoc的关系来估计最大功率点,使光伏阵列的初始工作点位于最大功率点附近,进而利用扰动观察法得到最大功率点,此种算法虽能较好地解决传统扰动观察法的缺点,但其复杂的计算限制了其应用范围。
针对于固定的扰动步长无法同时兼顾稳态时效率以及动态时的反应速度,许多研究者提出了变步长的跟踪方式。文献[14]设计一种三点比较式变步长扰动观察法,即通过三个点来比较,比较周期是传统扰动观察法的两倍,采用变步长,能更快地到达最大功率点并稳定下来,且稳定前的抖动值也有所降低,但从文献中提供的仿真图可看出该方法还有较大的提升空间。文献[15]中Patel等人根据光伏电池输出功率P的变化划分出四个阶段的步长值,当P与最大功率点Pmax之间的差值小于某一较小常数时,则假定光伏电池工作在最大功率点,扰动步长值为0。文献[16]提出一种基于电流预测控制的自适应变步长方法,该方法结合了自适应变步长控制器和电流预测控制器两种方法各自的优点,使其系统具有很好的静、动态性能。逐步逼近法的变步长扰动观察法能很好地克服固定步长扰动观察法的缺点,但在最大功率点附近需通过多次扰动才能实现稳定运行,文献[17]提出了基于梯度寻优思想的变步长算法,在扰动过程中按照P-U特性曲线的斜率而自适应改变扰动步长,进而实现系统寻优效率的提高。
针对光照条件下降较快时dP/dU变化较大而引起的跟踪动态特性和精度下降的问题,对变步长区域判别方式及步长形式进行了改进,提出一种改进型变步长扰动观察法。
1 光伏电池数学模型
光伏电池等效电路如图1所示,由图可得光伏电池数学模型为[18-19]:

式中Iph为流过PN结的漏电流;I0为反向饱和电流,其数量级为10-4A;q为电子的电荷,1.6×10-19C;K为玻尔兹曼常数,1.38×1023J/K;A为常数因子,介于1和2之间;T为绝对温度,单位为K;Rs为光伏电池串联电阻,一般在10-5Ω~1Ω之间;Rsh为光伏电池的并联电阻,可为数千欧。

图1 光伏电池等效电路Fig.1 Solar photovoltaic battery equivalent circuit
化简式(1)得到光伏电池数学工程模型:
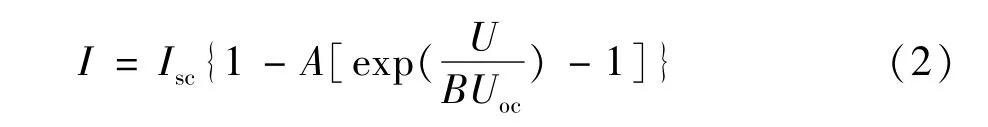
式中A、B为两个待定系数,通过求解得到:

式(2)是在标准条件下即参考温度Tref=25℃,参考日照强度Sref=1 000 W/m2的模型,当光照强度Sref=1 000 W/m2与电池温度发生变化时需要加以修改式(5)来描述新的特性曲线,可以做以下等效变换得到太阳能光伏电池的等效数学模型和输出特性。
令 ΔT=T-Tref,ΔS=S/Sref-1,得:

式中a、b、c取值为:a=0.002 5/℃,b=0.5,c=0.002 88/℃。只要利用式(5)求得光照强度和温度变化时的再利用式(3)、式(4)求得A′和B′,进一步利用式(2)解决任意光照强度和温度下的输出特性计算问题。
根据式(2)~式(5),通过 Matlab/Simulink建立光伏电池仿真模型,绘制标准条件下(Tref=25℃、Sref=1 000 W/m2)光伏电池输出特性曲线如图2所示。

图2 光伏电池输出特性曲线Fig.2 Photovoltaic cell output characteristic curve
仿真结果与实际光伏电池特性一致,说明光伏电池仿真模型的准确性。
2 改进的变步长扰动观察法
传统的变步长扰动观察法步长扰动表达式[20]为:

式中α为正数,即变步长速度因子,用于调整跟踪速度。
当工作点离最大功率点较近时采用式(6)作为扰动步长,减小系统最大功率点处的功率振荡;当工作点离最大功率点较远时,采用固定的大步长ΔU快速靠近最大功率点。
图3为光伏电池U—dP/dU特性曲线[21]。当光照强度为1 000 W/m2时变步长区域为d1,当光照强度为400W/m2时变步长区域变为d2,较d1范围增大,说明系统过早进入变步长区域,动态特性变差。当环境发生突变时,传统扰动观察法可能发生误判导致MPPT控制失效。
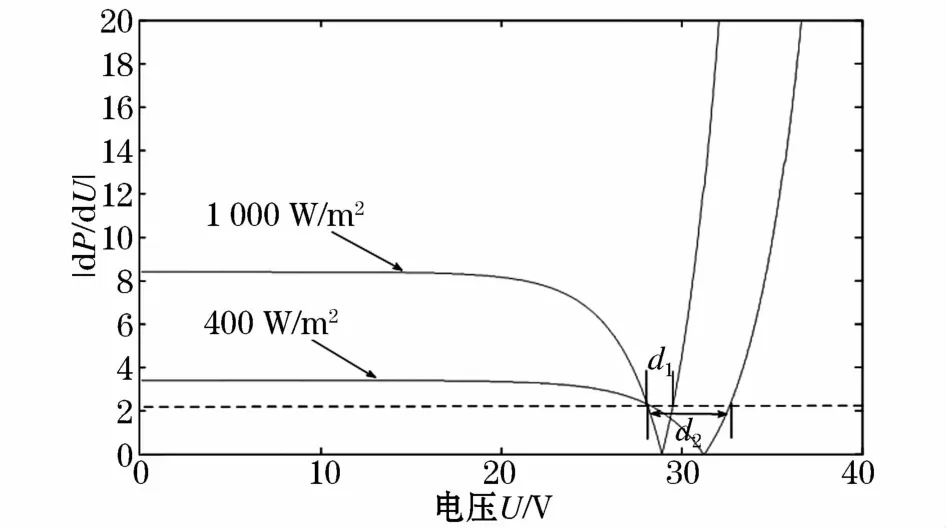
图3 光伏电池U—d P/d U特性曲线Fig.3 Photovoltaic cell U—d P/d U characteristic curve
针对以上两个问题,对传统变步长扰动观察法进行了改进:
(1)改变了变步长区域电压扰动表达式和变步长区域的判别方法;
(2)当检测到环境发生突变时,不对电压进行扰动,避免系统出现误判。改进的变步长扰动方式如下:
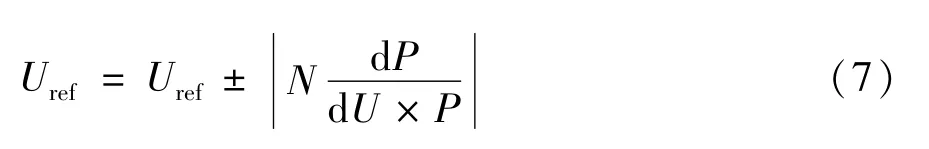
式中N为步长的速度因子,用于调整跟踪速度。

图4 光伏电池特性曲线Fig.4 Photovoltaic cellcharacteristic curve
改进后步长选择条件及相应的步长区域为:

式中ΔU为电压的扰动量;U1、U2为步长的选择阀值,且U1>U2。
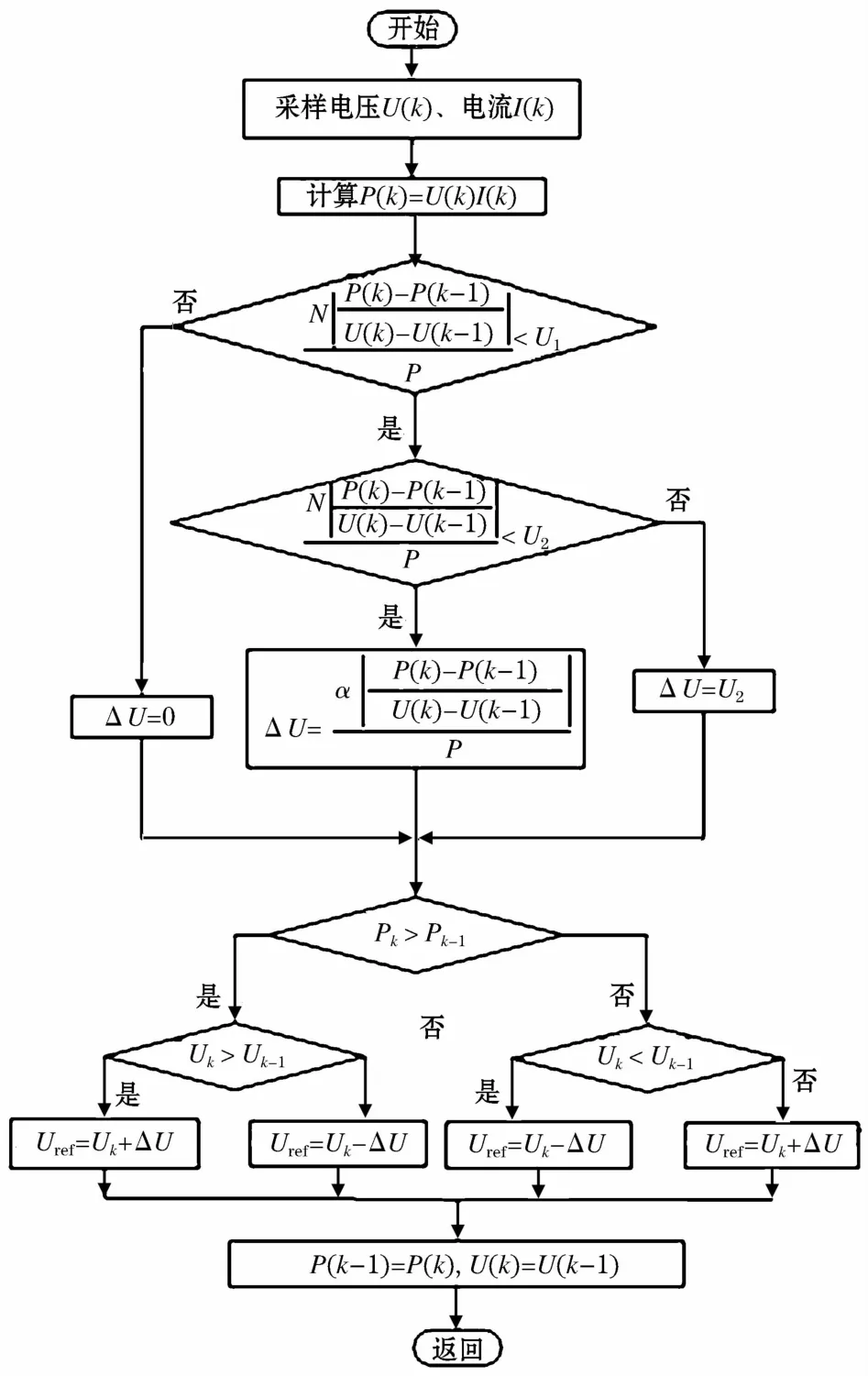
图5 改进的变步长扰动观察法流程图Fig.5 Flow chart of the improved variable step size P&O method
3 仿真研究
以3 kW光伏逆变器作为研究对象,采用单级式主电路拓扑结构和LCL网侧滤波器,主电路及其控制策略如图6所示[19,22]。逆变器采用双闭环控制策略,外环为直流电压环,直流电压给定为MPPT模块的输出;内环为电流环,控制并网电流与电网电压同频同相。
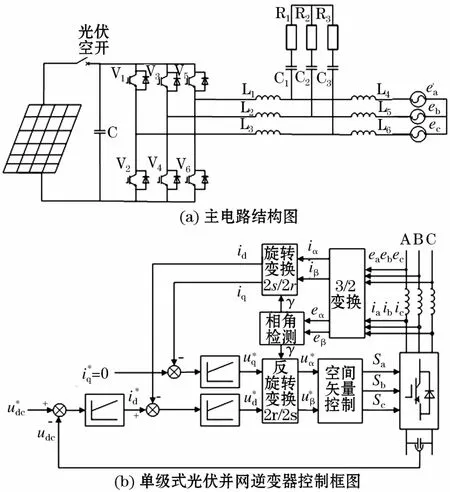
图6 主电路及其控制框图Fig.6 Main circuit and its control block diagram
为了验证改进算法的有效性,基于MATLAB/Simulink搭建系统仿真模型。采用的光伏电池参数如下(标准外界环境下):开路电压Uoc=37 V,短路电流Isc=8.4 A,最大功率点电压Um=30 V,最大功率点电流Im=7.8 A,最大功率点功率Pm=234 V。电路参数为:直流母线电容C=2 200μF,滤波电感L1=L2=L3=1.2 mH,L4=L5=L6=1.5 mH,交流侧滤波电容C1=C2=C3=9.4μF。
仿真中,设置环境温度为25℃,仿真时间设置为0.4 s,采样周期为0.01 s。在0.2 s时外界光照强度由1 000W/m2突变为400W/m2,观察传统变步长扰动观察法和改进后系统的MPPT参考电压和光伏电池输出功率的变化情况。图7、图8为传统的扰动观察法MPPT参考电压和光伏电池输出功率,0.2 s之前系统经过启动过程稳定在最大功率点附近,在0.2 s时光照强度发生突变,系统跟踪新的最大功率点,系统经过17个采样周期才跟踪到最大功率点从图7可得系统过早进入变步长阶段,导致动态性能变差。

图7 传统扰动观察法MPPT参考电压曲线Fig.7 MPPT reference voltage curve of traditional P&O method

图8 传统扰动观察法光伏电池功率曲线Fig.8 Photovoltaic power curve of traditional P&O method
将传统扰动观察法步长选择的阀值减小,使系统不会过早进入变步长阶段,提升系统的动态性能,但是在稳态时又会导致较大的功率波动,如图9、图10所示。

图9 传统扰动观察法MPPT参考电压曲线Fig.9 MPPT reference voltage curve of traditional P&Omethod
图11、图12为改进后的扰动观察法MPPT参考电压和功率曲线,0.2 s光照强度由1000 W/m2突变为400 W/m2,系统经过8个采样周期跟踪到最大功率点,并且能够在最大功率点附近稳定运行,功率波动和参考电压波动很小。

图10 传统扰动观察法光伏电池功率曲线Fig.10 Photovoltaic power curve of traditional P&O method

图11 改进的扰动观察法MPPT参考电压曲线Fig.11 MPPT reference voltage curve of improved P&O method
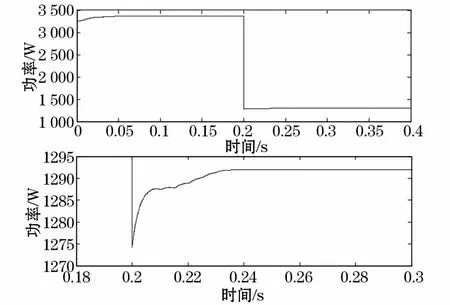
图12 改进的扰动观察法光伏电池功率曲线Fig.12 Photovoltaic power curve of improved P&O method
根据上述比较分析可以看出,改进的扰动观察法能够在外界环境变化较大时,保证系统有较好的稳态性能和动态性能。
4 实验研究
图13为在3 kW单级式光伏发电系统实验平台上采用传统的变步长扰动观察法控制时,光伏电池的输出功率变化曲线,系统初始运行条件温度25℃,光照条件400 W/m2,光伏电池输出功率1 700 W,当温度不变,外界光照条件突变为1 000 W/m2时,系统经过大约0.5 s跟踪到最大功率点3 000 W处稳定运行。

图13 传统变步长扰动观察法光伏电池输出功率Fig.13 Photovoltaic output power of traditional P&O method
图14为改进后变步长扰动观察法光伏电池功率变化曲线,外界条件变化及初始状态与图13相同,系统跟踪最大功率点的速度明显提高,经过0.2 s跟踪到最大功率点处。说明MPPT控制算法的改进能够在外界条件变化较大时,提高MPPT跟踪的动态性能。
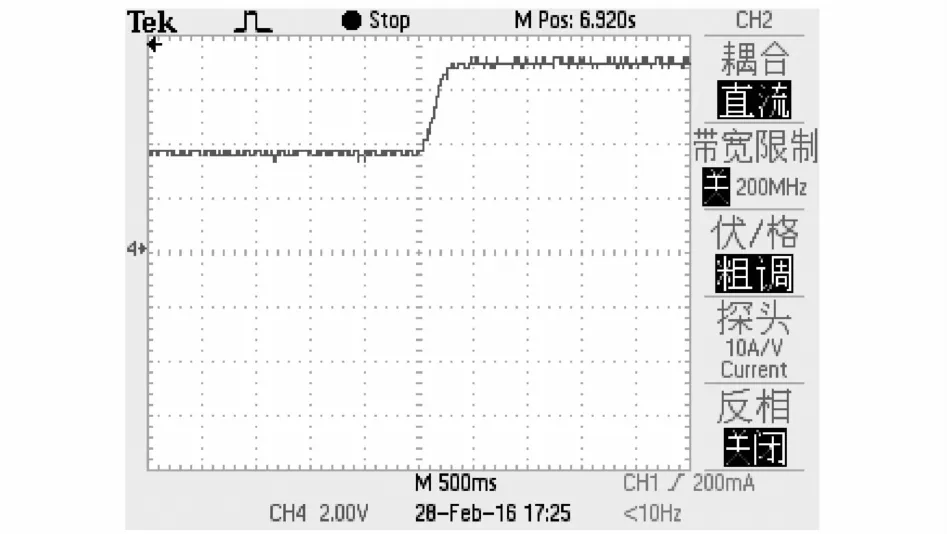
图14 改进的变步长扰动观察法光伏电池输出功率Fig.14 Photovoltaic output power of improved P&O method
5 结束语
针对光伏发电中的最大功率点跟踪技术,对传统扰动观察法进行改进,改变步长的判别方式和步长因子,提出一种改进的变步长扰动观察法,在外界环境变化较大时可以保持很好的动态特性和稳态精度。
