四驱汽车分动器轴承力学特性分析与试验

胡 芳,谭雨点,王 亮,陈黎卿

(1.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009; 2.安徽农业大学 工学院,安徽 合肥 230036)

四驱汽车分动器轴承力学特性分析与试验

胡 芳1,谭雨点2,王 亮2,陈黎卿2

(1.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009; 2.安徽农业大学 工学院,安徽 合肥 230036)

针对四驱汽车传动系统分动器轴承载荷难以确定的问题,文章提出并推导了轴承力学特性分析公式。以某款四驱汽车分动器为例,构建了分动器各传动轴的空间力学模型,在此基础上推导出齿轮、轴承等部件的力学矩阵方程,从而求解出齿轮、轴承的各方向力学载荷;以90 N·m输入工况为例,建立轴承有限元分析模型,运用推导出的力学载荷公式对其进行有限元分析与压力测试试验数值对比,得出轴承的有限元分析与试验应力误差为5.23%,验证了该公式的正确性;同时进行了极限工况下的轴承应力分析,研究成果为轴承在该类部件的设计提供了一定的依据。

分动器;轴承;受力分析;仿真;压力测试

四驱汽车传动系统分动器部件中轴承的受力载荷情况直接影响到应力分布及疲劳寿命,从而影响部件的工作性能,因此,对于轴承力学特性分析显得尤为重要。国内外学者在此方面均开展了诸多探索研究。文献[1]对齿轮系统的相互接触受力进行了有限元分析;文献[2]对智能四驱汽车分动器壳体进行了有限元分析和模态试验;文献[3]对具有塑性变形的转盘轴承进行了有限元分析;文献[4]对滚动轴承进行了有限元分析;此外诸多学者还在汽车传动系统内部齿轮-轴传动机构分析和接触受力分析等方面开展了系列研究[5-10]。通过对现有研究成果的分析可知:针对汽车传动系统中轴承部件的力学分析较少,对其传动部件力学分析往往以有限元分析为主,有限元分析的输入也多以简化模型代替,例如对于轴承和齿轮等部件的研究,均为将动力输入载荷直接加载到被分析部件,使得分析结果数值偏大;另一方面,轴承受力载荷的确定由软件建模仿真得到,其载荷大小的准确度也难以得到验证。

本文以某款四驱汽车传动系统中的典型部件——分动器为研究对象,通过对内部传动系的分析建立轴承所受载荷的理论公式,并进行试验对比,以验证所推导轴承载荷的正确性。

1 分动器力学模型构建

1.1 分动器传动部件的模型建立

典型四驱汽车分动器结构示意图如图1所示。动力从左边输入,经过2级传动后从传动轴5、7分别输出,2级齿轮分别为圆柱斜齿轮1、2和双曲面锥齿轮3、4,轴承A、B、C、D、E、F分别安装在传动轴5、6、7上,均为圆锥滚子轴承。

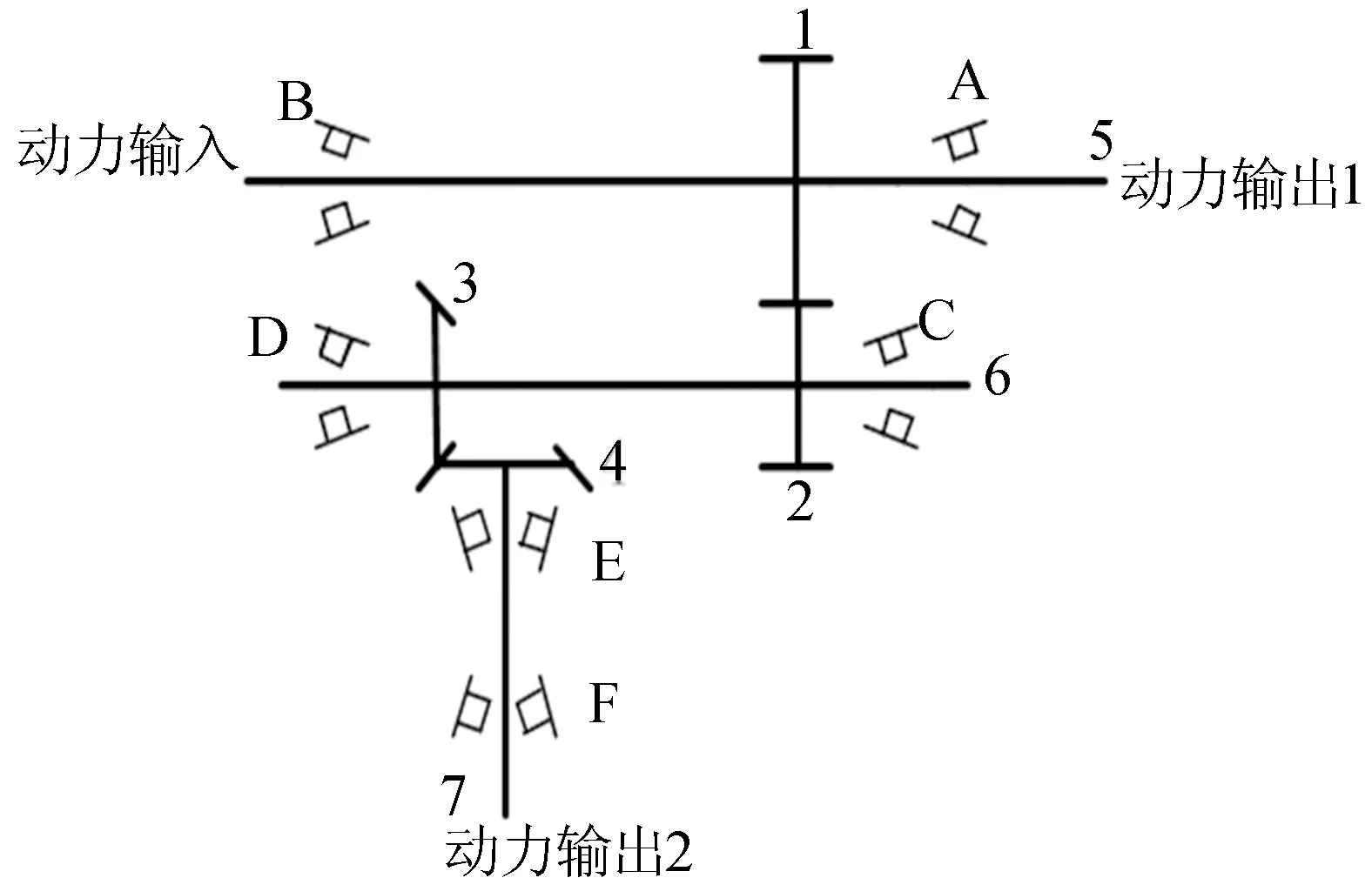
图1 分动器总成示意图

1.2 分动器齿轮的受力分析

[11],经推导可得斜齿轮与锥齿轮的力学公式。斜齿轮受力方程组为:

(1)

锥齿轮受力方程组为:

(2)

其中,T为斜齿轮输入扭矩;d为斜齿轮的分度圆直径;α′、β分别为斜齿轮压力角、螺旋角;z、m分别为斜齿轮齿数、模数;Ft、Fr、Fa分别为斜齿轮上产生的圆周力、径向力、轴向力大小;T′为锥齿轮输入扭矩;d′为锥齿轮的分度圆直径;α″、β′、γ分别为锥齿轮法向压力角、平均螺旋角、节锥角;Ft′、Fr′、Fa′分别为锥齿轮上产生的圆周力、径向力、轴向力大小。

1.3 分动器各传动轴力学模型

1.3.1 输入轴力学模型

传动轴5受力分析模型主要包含斜齿轮、轴和支撑圆锥滚动轴承体系,通过(1) 式可以获得主动齿轮的受力情况,由此建立传动轴5的受力分析模型如图2所示。

其中，圆锥滚动轴承的轴向力需要通过轴向力判断准则[11]来确定。

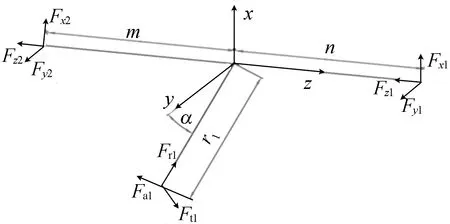
图2 传动轴5受力分析模型

A1X1=B1

(3)

(4)

(5)

(6)

其中,m为斜齿轮与轴承B的距离;n为斜齿轮与轴承A的距离;r1为斜齿轮1的半径；Fs为各个轴承的附加轴向力大小；Fx、Fy、Fz为径向力的分解力。

1.3.2 中间轴力学模型

建立传动轴6的受力分析模型,中间轴主要由圆柱斜齿轮、轴、锥齿轮以及支撑轴承组组成,获得轴的锥齿轮受力情况后并建立受力模型,如图3所示。其中,e为锥齿轮3与轴承D的距离;f为斜齿轮2与锥齿轮3的距离;dm为斜齿轮2的半径;g为锥齿轮3与轴承C的距离。

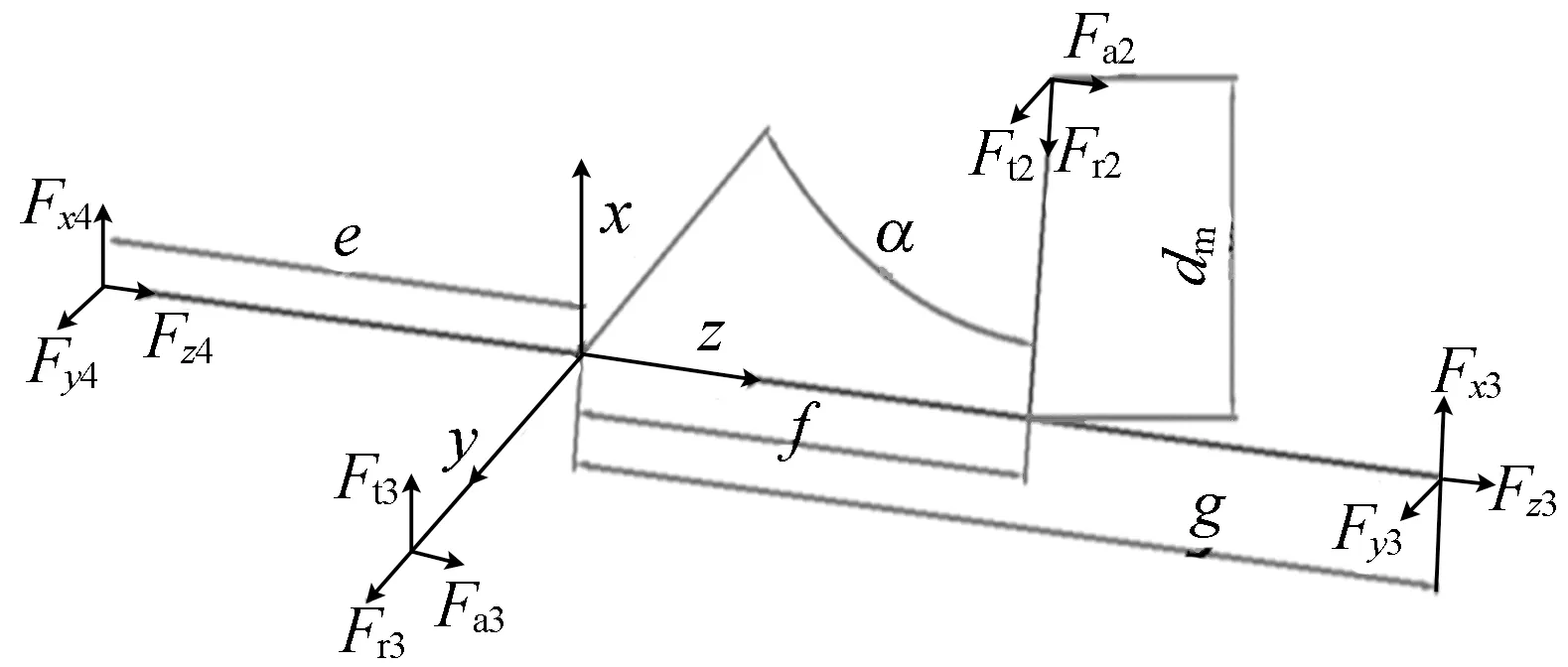
图3 传动轴6受力分析模型

A2X2=B2

(7)

(8)

(9)

(10)

1.3.3 输出轴力学模型

传动轴7的受力分析输出轴的受力模型,如图4所示。

图4中,dm为锥齿轮4的半径;c为锥齿轮4与轴承E的距离;d为锥齿轮4与轴承F的距离。

对传动系统中齿轮受力进行理论分析后建立各个传动轴的空间力学模型,并根据各轴承的受力，在对其轴向力判断方向后建立总的受力平衡矩阵,最终确定各轴上圆锥滚动轴承在各空间方向的载荷值。

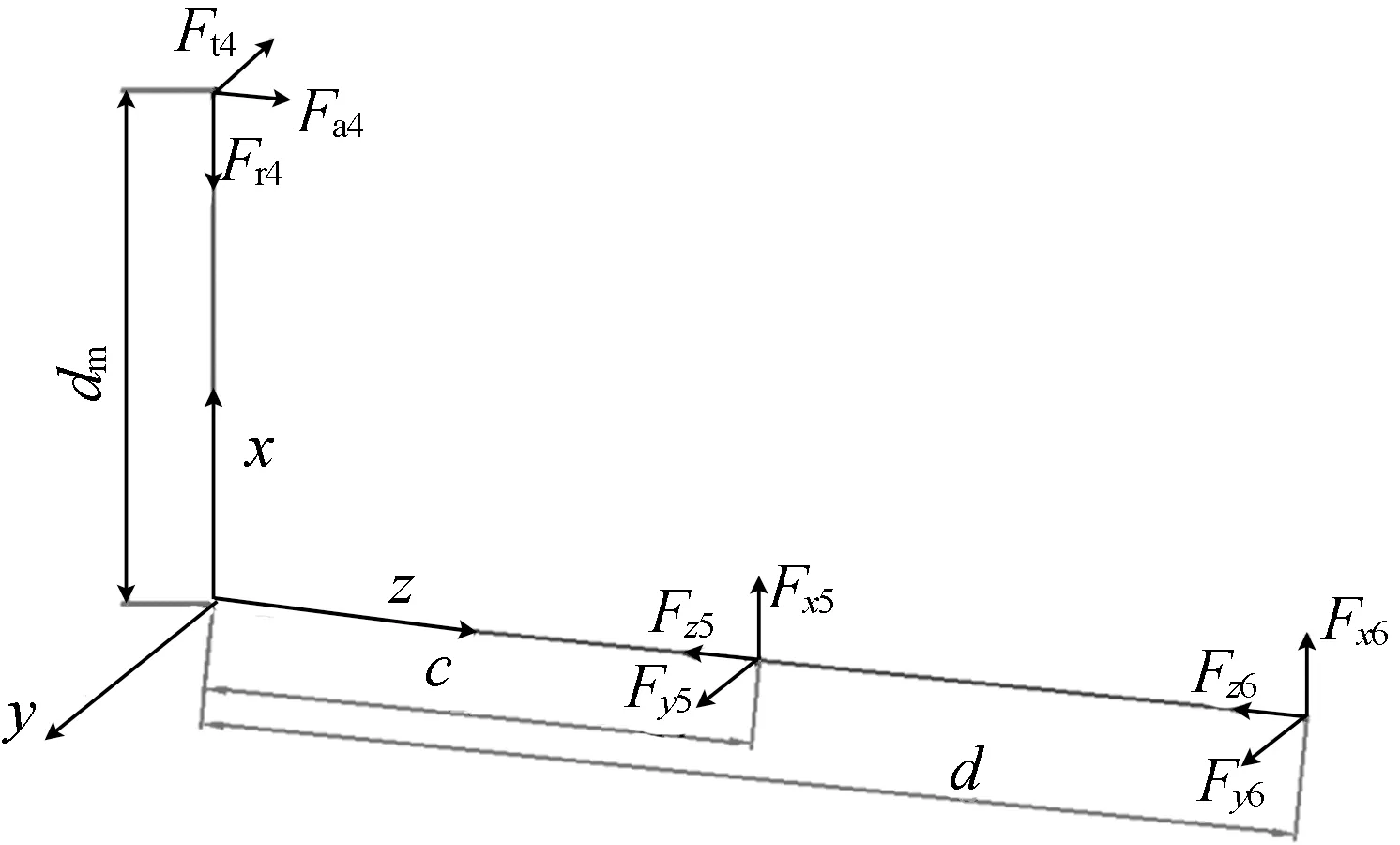
图4 传动轴7受力分析模型

A3X3=B3

(11)

(12)

(13)

(14)

2 试验验证

2.1 分动器有限元模型构建

以某款四驱汽车分动器为研究对象,建立分动器UG三维模型,导入Abaqus进行划网格、加载边界条件,在保证计算精度的情况下对轴承模型进行简化[12],分动器有限元模型如图5所示。

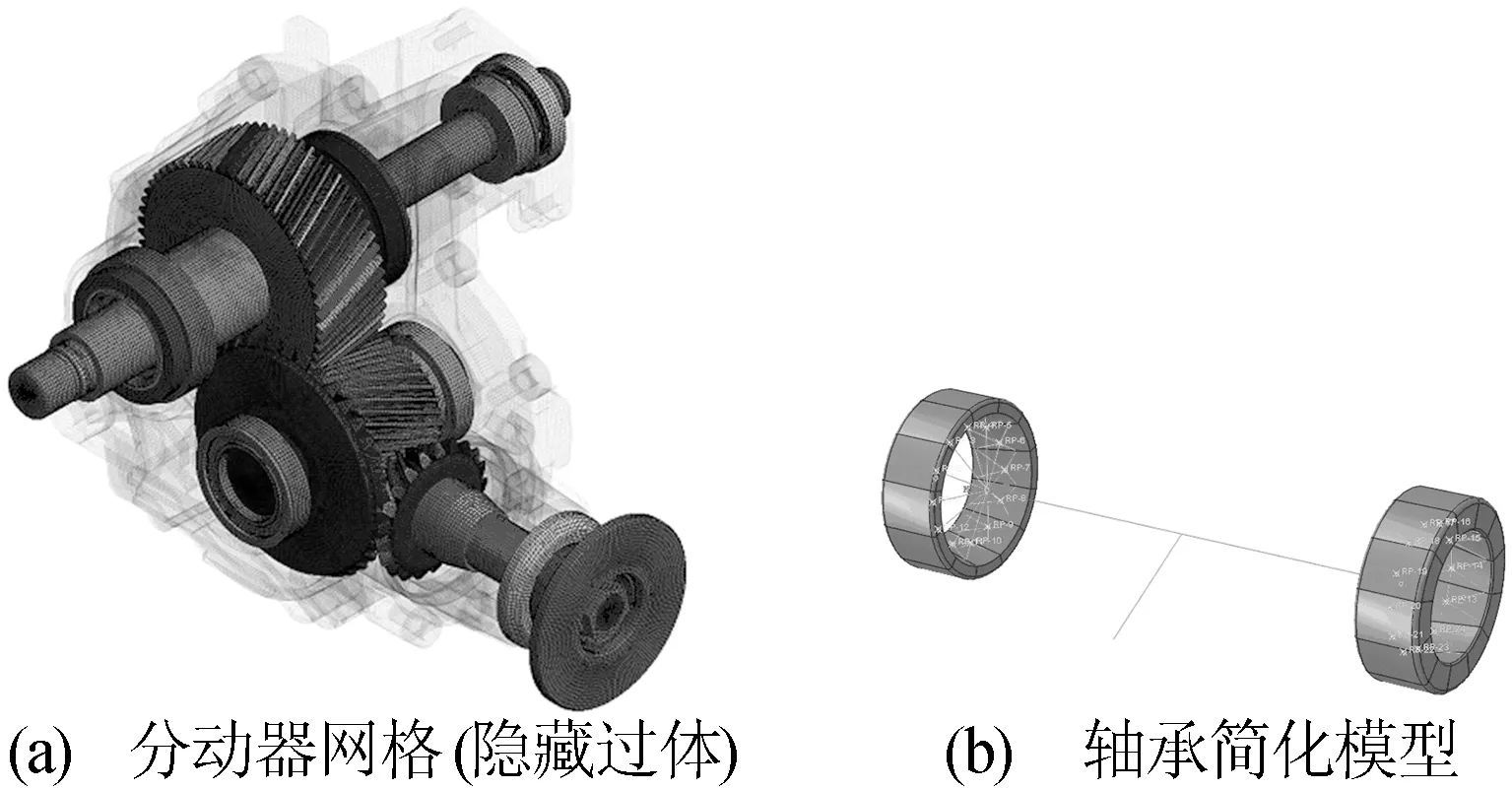
图5 分动器有限元模型

分动器相关参数见表1所列。

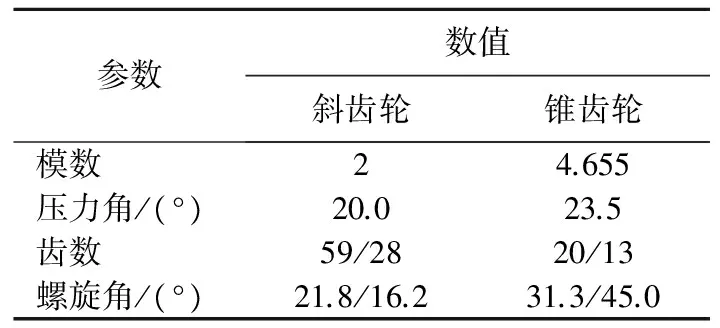
表1 分动器参数

设定输入扭矩90 N·m,通过本文建立的矩阵得出轴承各个方向的受力载荷，见表2所列,再经过有限元分析得到轴承的应力分布。

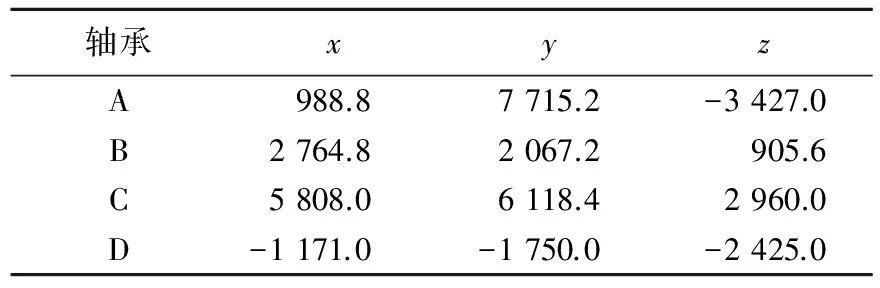
表2 轴承受力分布 N

2.2 分动器试验设计

为验证本文轴承受力分析公式对计算轴承各个方向载荷数值的准确性和可靠性,针对某款分动器内部传动系上的轴承应力分布进行压力试验测试。试验现场如图6所示。传动试验台主要由三相异步电机驱动,通过中央控制装置实行可调负载的试验台,试验采用富士压力测试胶片进行试验测试。将装配压力测试纸的轴承通过专业工具装入分动器内部,当传动系统施加负载后,轴承外圈表面将会产生压力,从而使得测试胶片纸出现颜色变化,反映试验结果。由于该测试胶片在无油条件下进行,达不到极限工况的测试要求,本次试验选取90、180 N·m分别作为输入扭矩进行试验,完成后取出压力测试纸进行分析,选取4块区域的应力值进行记录。选取该分动器的A、B、C、D 4个轴承外圈应力作为测试对象。

图6 传动试验图

试验时先选取输入扭矩90 N·m作为动力输入,按照试验条件及步骤完成试验后,拆开分动器,取下压力测试纸,通过富士压力测试装置专业扫描仪获取试验结果。最后将同等载荷条件下的仿真结果与压力试验结果进行对比,对比结果如图7所示。

图7 仿真与试验结果的对比

由图7a可知,在接触区域内压力分布大体相同,同时在应力最大的区域内仿真结果与试验结果也基本吻合。

由图7b可知,由于在拆卸过程中,轴承外圈发生偏斜,导致局部区域的压力超过压力传感器的量程,但通过与仿真结果对比,该区域的压力分布云图趋势依旧与仿真结果保持一致。

由图7c可知,在输入扭矩90 N·m的工况下,通过对选取的4部分仿真与试验结果进行对比，得出其误差值均在5%以内,说明仿真情况与试验结果基本相同。

2.4 分动器静力学分析

运用所推导分动器力学公式,对该款产品进行极限工况下的静力学分析,得出分动器的应力应变结果如图8所示。

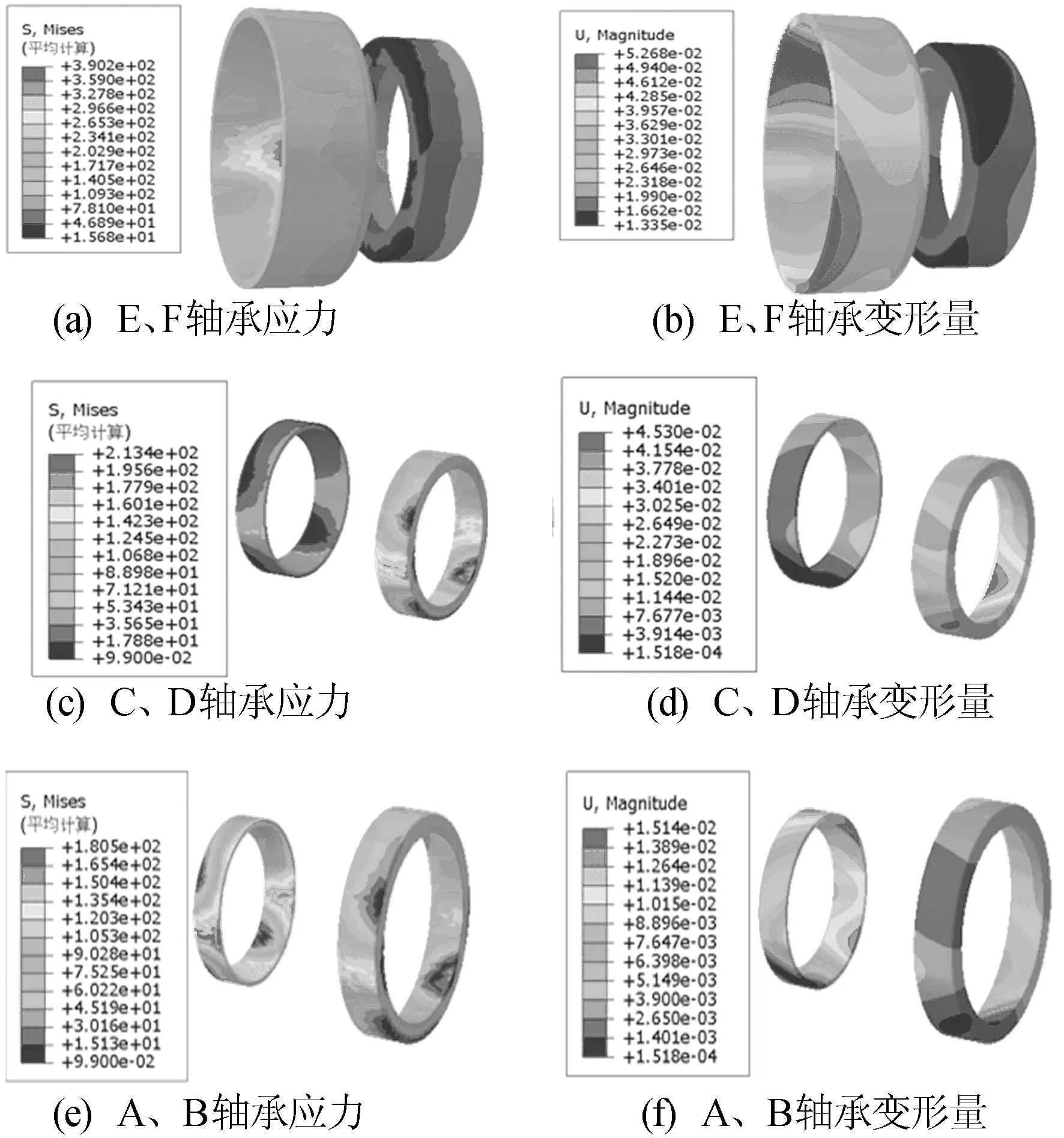
图8 分动器应力、变形云图

由图8a和图8b可以看出,圆锥滚动轴承E、F的最大应力为390.0 MPa,最大变形量为0.055 mm;靠近小锥齿轮的圆锥滚动轴承E的应力明显大于远离小锥齿轮的圆锥滚动轴承F,因此在选择轴承时,以轴承E的强度为标准,选择配套的圆锥滚动轴承F。由图8c和图8d可以看出,圆锥滚动轴承C、D的最大应力为213.4 MPa,最大变形量为0.045 mm; C、D为中间轴支承轴承,C靠近小圆柱斜齿轮端,C的整体应力均比D要大,而且能够明显地看出C轴承外圈出现了应力较大区域,因此在选择C、D轴承对时,以C轴承的强度为标准选择D轴承。由图8e和图8f可以看出,圆锥滚动轴承A、B的最大应力为180.5 MPa,最大变形量为0.015 mm;A、B为输入轴端轴承,其中A靠近大圆柱斜齿轮端,其应力整体值偏大,因此,在选择A、B轴承对时,以轴承A的强度为参考标准,选择B轴承。

3 结 论

(1) 本文通过建立传动模型矩阵公式，推导出了分动器轴承力学公式,并对输入扭矩为90、80 N·m工况下的载荷值进行计算和压力测试试验;试验数据对比可得,在90 N·m工况下应力误差在5.23%以内,180 N·m工况下误差在10%以内,验证了本文轴承力学公式的正确性。

(2) 在此基础上,以某款分动器为研究对象,对其进行分动器有限元分析,得出了轴承部件的应力和应变图,并给出了轴承设计的参考依据,为轴承在该类产品的设计提供一定的参考。

[参考文献]

[1] 陈黎卿,陈无畏,王钰明，等.智能四驱汽车分动器壳体有限元分析与模态试验[J].中国机械工程,2013,24(12):2168-2172.

[2] CHO J R,JEONG K Y,PARK M H.Finite element structural analysis of wind turbine gearbox considering tooth contact of internal gear system [J].Journal of Mechanical Science and Technology,2013,27 (7):2053-2059.

[3] 尚振国,董惠敏,毛范海,等.具有塑性变形的转盘轴承有限元分析方法[J].农业工程学报,2011,27(12):52-56.

[4] 徐弘毅,张晨辉.基于塑性材料模型的滚动轴承有限元分析[J].机械工程学报,2010,46(11):29-35.

[5] 唐进元,刘艳平.直齿面齿轮加载啮合有限元仿真分析[J].机械工程学报,2012,48(5):124-131.

[6] 童宝宏,刘颖,程新明,等.轴颈倾斜时滚柱轴承动态接触特性的有限元分析[J].农业工程学报,2012,28(13):42-47.

[7] 邓玫,孙军,符永红,等.计及轴受载变形的粗糙表面轴承热弹性流体动力润滑分析[J].机械工程学报,2010,46(15):95-101.

[8] PUROHIT R K,PUROHIT K.Dynamic analysis of ball bearings with effect of preload and number of balls[J].Int J of Applied Mechanicsand Engineering,2006,11(1):77-91.

[9] ZHANG Y Q,TAN Q C,LI J G,et al.Fatigue life of taper roller bearings in drive rear axle main gear reducer[J]Advanced Materials Research,2012,510:112-116.

[10] 杨霞,鄢闯,肖宏,等.利用轴承边界元法分析轴向力对四列圆锥轴承载荷的影响[J].机械设计与研究,2014,30(2):72-75,79.

[11] 濮良贵,陈国定,吴立言.机械设计[M].北京:高等教育出版社,2013.

[12] 王亮,胡芳,陈黎卿,等.汽车传动系统非规则壳体类部件有限元建模[J].机械强度,2016,38(1):122-127.

Analysisandexperimentonmechanicalcharacteristicof4WDautomobiletransfercasebearings

HU Fang1,TAN Yudian2,WANG Liang2,CHEN Liqing2

(1.School of Automobile and Traffic Engineering, Hefei University of Technology, Hefei 230009, China; 2.School of Engineering, Anhui Agricultural University, Hefei 230036, China)

Based on the uncertain problem of transfer case bearing load of the four-wheel drive(4WD) automobile transmission system, the bearing mechanical characteristic formula was put forward and deduced. Taking a 4WD automobile transfer case as an example, the spatial mechanical model of each transfer transmission shaft was built. On this basis, the mechanical matrix equation of gears, bearings and other parts was derived, and the each directional mechanical load of the gears and bearings was solved. Under the condition of input torque of 90 N·m, the finite element analysis model of transfer case was set up, and the results of the simulation applying the mechanical load formula were compared with the results of pressure test. The results show that the stress error of each bearing between simulation and test is 5.23%, which verifies the reliability of the mechanical load formula. Finally, the bearing stress analysis under limiting conditions was carried out. The research results can provide a basis for the design of the bearing on this kind of transfer case.

transfer case; bearing; mechanical analysis; simulation; pressure test

2016-10-10；

2017-01-07

国家自然科学基金资助项目(51305004)

胡 芳(1968-),女，安徽太和人,合肥工业大学副研究员.

10.3969/j.issn.1003-5060.2017.11.005

TH133.3

A

1003-5060(2017)11-1464-05

(责任编辑 胡亚敏)