多绕组变压器＋变流器结构中高频谐波分析与抑制

王毅，李尚盛，杨泽洲，吴楠，李琼林，孙建军

（1.武汉大学电气工程学院，武汉430072；2.国网河南省电力公司电力科学研究院，郑州450052）

0 引 言

受电力电子开关器件耐压和容量的限制，高电压、大容量电力电子设备常采用器件串并联或多重化技术。多重化技术是指将多个低电压等级、小容量的变流器模块按照一定的拓扑组合起来，实现高压大容量输出的技术。其主要可分为：（1）模块直接串联，如级联H桥多电平（CHB）［1］、模块化级联多电平（MMC）［2］等；（2）模块直接并联，如并联运行的APF等；（3）通过多绕组变压器连接，如早期的STATCOM［3］等。其中，第三种结构中的多绕组变压器使得各个模块之间均流简单，能量分配均匀，因此是早期的大功率电力电子设备常采用的结构。另外，此结构中各个模块之间完全电气隔离，满足级联多电平的基本要求。在需要有功输出的级联多电平拓扑中，广泛使用该结构提供独立的直流侧电压，其中典型应用有：中高压变频器［4］、电力电子变压器［5-6］、扰动发生器［7］等。

无论何种结构的变流器，均存在一定的特征谐波，这些谐波在多绕组变压器中传播会引起变压器的噪声增加、损耗增加以及磁路饱和等问题。一旦这些谐波通过多绕组变压器流入电网，又会对电网造成污染，导致电能质量问题。当变流器为不控整流或相控整流时，其特征谐波主要分布在低频，可以使用多绕组变压器绕组移相接法来消除［8］。当变流器是PWM全控型变流器时，其特征谐波分布和开关频率有关，频率较高，难以通过绕组移相来消除。而高频谐波流入系统，可能会对邻近设备产生诸多不利影响，如：附加谐波损耗，噪声，减少设备使用寿命，干扰通讯，影响设备的正常运行，严重的甚至造成设备损坏［9-10］。另外，对于PWM变流器中由死区或控制等原因引起的低频谐波，则可以通过优化控制本身得以改善。

对于开关谐波的抑制，常用做法是在每一个变流器模块交流侧增加滤波支路［11］。这种方法虽然可以有效地滤除谐波，但是会增加成本，增大损耗；同时引入谐振，导致系统稳定性问题，降低系统可靠性［12-14］。另一种方法是提高每一个模块的PWM开关频率，让开关谐波处于较高的频段［15］。对于较高频率的谐波，通过连接电抗和变压器自身阻抗即可阻隔，但是这种方法会大大增加开关损耗。而且受到器件性能的限制，开关频率难以大幅提高［16］。第三种方法是通过调制和控制手段，让部分开关谐波相互抵消。在不增加硬件电路和模块开关频率的情况下，提升了整体的开关谐波频带。

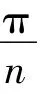
1 经多绕组变压器并联的变流器

单相多绕组变压器＋单相H桥变流器结构如图1所示。其中：us为系统电压；rs、ls为系统等效电阻与等效电感；l2i为第i个变流器的连接电感；uci为第i个单元输出电压；udci为第i个单元的直流电压；u1为变压器原边电压；u2i为第个绕组电压。

图1 多绕组变压器＋H桥变流器拓扑Fig.1 Topological graph containing multi-winding transformer and H-bridge converters

为简化分析，对图1所示的拓扑结构作如下前提假设：

（1）系统电压us为理想电压源；

（2）拓扑中不含滤波支路；

（3）不考虑直流电压的波动，即udci＝Udci；

（4）各变流器调制方式及开关频率一致。

2 高频谐波传输等效模型

2.1 H桥变流器高频谐波特性

H桥变流器根据调制方式的不同可以分为双极性、单极性和单级倍频三种。其中，单级倍频调制方式具有直压利用率高、等效开关频率高的特点，应用最为广泛。本文的H桥逆变器即采用单级倍频方式，以单元i为例，变流器输出电压uci可表示为［17］：

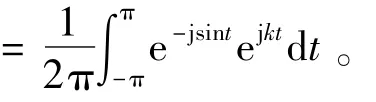
式（1）右边第一项对应与系统电压同频的基波分量，第二项即对应本文所要分析的高频分量，为简化分析，将其用uhi表示：

2.2 多绕组变压器等效模型

多绕组变压器的等效电路主要有多边形，梯形，射线形三种形式。当不考虑绕组间的参数差异时，可以采用射线形模型［18］，如图 2所示。其中：r1、lσ1分别为变压器原边等效电阻与电感；r2i、lσ2i为副边第i个绕组等效电阻与电感；rm、lm为等效励磁电阻与电感。

2.3 高频谐波传输等效模型

不考虑基波与低次谐波分量，H桥变流器可等效为高频谐波电压源＋连接电感，其谐波含量如式（2）。不考虑系统引入的高频谐波，考虑多绕组变压器模型的高频谐波传输等效模型如图3所示。

图2 多绕组变压器射线形模型Fig.2 Ray model of a multi-winding transformer

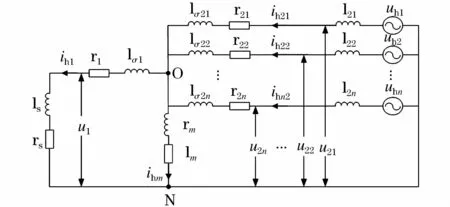
图3 高频谐波传输等效模型Fig.3 Equivalent model of high frequency harmonic transmission

图中，“N”为参考节点；“O”为变压器虚拟中点；ih1为变压器原边高频谐波电流；ih2为副边第i个绕组的高频谐波电流；ihm为变压器高频谐波励磁电流。

如图3所示，高频谐波源为变流器，由PWM调制技术引入。根据基尔霍夫电压、电流定律，可得变压器虚拟中点的表达式：

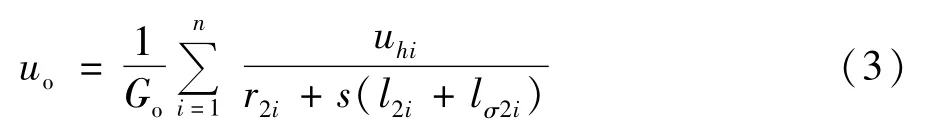
式中Go为“O”点的节点导纳。

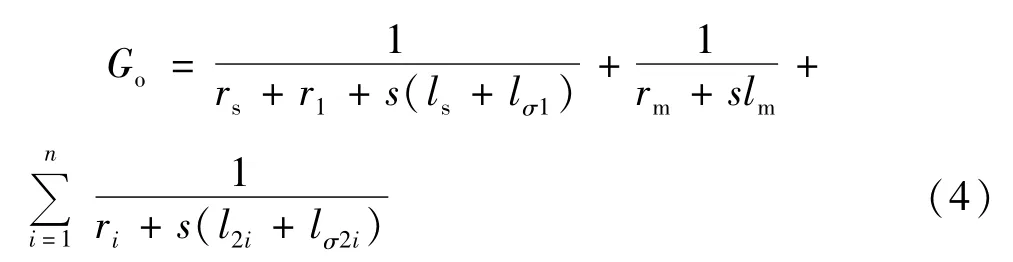
式（3）与式（4）中s的取值决定于电压uhi的基准频率，实际中，uhi具有很多频率成分，见式（2）。模型中的其它节点电压与电流，可表示成uo的表达式。

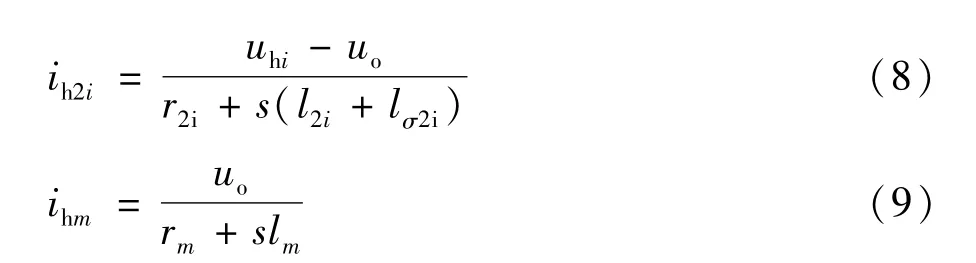
3 高频谐波传播特性分析

高频谐波的影响主要体现在变压器原边电压与电流中，对于变压器副边电流中的谐波分量可视为装置内部电流，而不予考虑。为进一步简化分析，作如下假设：

（1）各绕组及变流器参数一致，即 lσ2i＝lσ2、l2i＝l2、r2i＝r2；

（2）各变流器直流侧电压一致，即Udci＝Udc；

（3）考虑uhi中某一频率分量，即：

基于以上假设，可将某一频率下的虚拟中点电压描述为：

3.1 载波同相

当载波同相位时，u0（m，k）由n个变流器叠加：

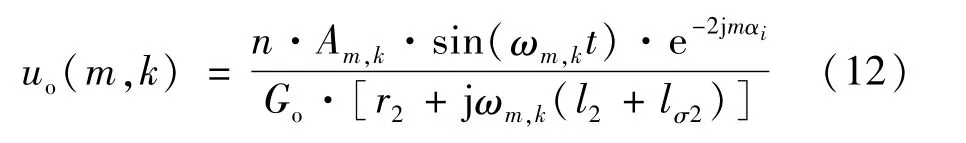
由于｜e－2jmαi｜＝1，所以此时 u0包含了 2kc倍的变频分量并且幅值最大，根据式（5）～式（9）可知：

（1）变压器原边电压电流中高频谐波分量最大，且是副边电流的线性叠加；

（2）变压器副边电压电流中高频谐波含量最小；

（3）变压器励磁电流中，高频谐波含量大。

3.2 载波移相

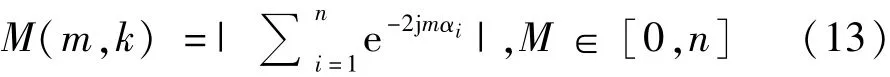
当时，各个变流器的谐波同方向线性叠加，谐波的幅值达到最大，载波的初始相位满足关系 αi＝αi－1，i＝1，2…n此时，各个单元同频谐波在铁芯内的磁动势具有相同的相位，同向线性叠加达到最大值，原边的谐波电压幅值达到最大。

当 M（m，k）＝0时，u0（m，k）＝0，此时高频谐波ωm，k的磁动势在磁芯中相互抵消，表现为变压器原边消除了 ωm，k次的谐波。同时，M（m，k）只和 m、αi有关和k无关，消除谐波2mωc时及其边带谐波2mωc＋kωs一并被消除。M（m，k）中可控变量为 αi，从相量的角度分析，αi均匀的分布在空间中可以实现相量和为零。

如图4所示，给出了单元数分别为3和4时，采用不同的载波初相角主要次谐波的抵消情况。其中，Δα为相邻变流器初始相位差即移相角度，Δα＝αi－αi－1；Δθ为相邻变流器各次谐波相角差，其中 Δθ＝2mΔα。载波的移相角度 Δα是 π／n，2π／n或者3π／n时，都可以实现谐波消除。

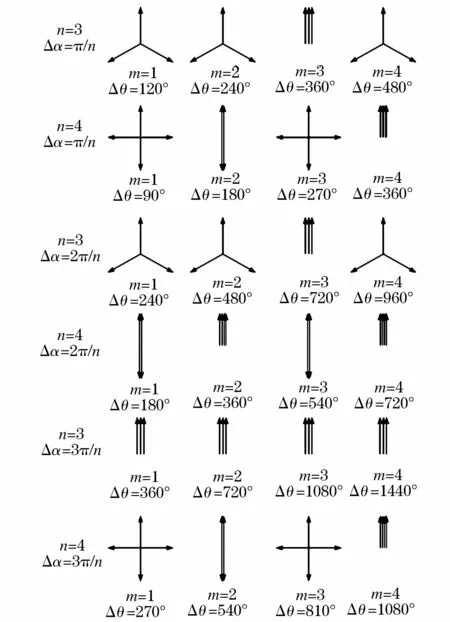
图4 不同的载波移相角度分析Fig.4 Analysis of carrier phase-shift from different angles

取Δα＝λπ／n，λ∈［1，n］，此时Δθ＝2π×mλ／n。Δθ是2π的整数倍即mλ／n为整数时，各个变流器的谐波相量同方向线性叠加，谐波幅值最大，最为不利应该避免。mλ／n为分数时，n个变流器的谐波相量可以均匀的分布在相量空间相互抵消，相量和为零。并且，各次谐波抵消的情况是以n为周期，1－n次谐波的相量抵消情况为一个周期。当λ＝1时，mλ／n＝m／n；λ＝2，3…n时，mλ／n是以 λ为间隔在 m／n中取值。当λ与n互质时，谐波消除情况最优和λ＝1时相同；当λ与n不互质时，一个周期n内可能增加谐波线性叠加的次数，劣于λ＝1的情况。例如，图4中n＝4时，Δα＝2π／n相比与 Δα＝π／n在一个周期内，谐波叠加的情况多了一倍。因此，选取载波移相的角度为π／n是最优的。

移相后，uo的高频谐波含量为：

可见，载波移相后，uo只含 2pnkc（p＝1，2…）及其边频的高频谐波。此时，由式（5）～式（9）可得到如下结论：

（1）变压器原边电压电流、励磁电流中高频谐波分量最小；

（2）变压器副边电压电流中高频谐波含量最大；

（3）变压器励磁电流中高频谐波含量小。

根据以上分析，当经过多绕组变流器并联的变流器个数较多时，可以采用载波互差π／n的方法抵消大部分高频谐波，使其无法传播到变压器原边。相比于在副边采用电容支路，缺点在于高频谐波会流入变压器副边，带来变压器损耗与噪声。优点在于减少了滤波支路，降低了谐振风险，提高了装置运行可靠性，也减小了通过H桥的高频谐波大小。

当载波不同步时，考虑各变流器的芯片时钟差异，其等效效果为各变流器载波初始相角呈随机分布，并随时间变化。载波同步且同相与载波同步且移相，是其中的两个特例。载波不同步时，uo的高频谐波含量介于两者之间。

考虑到不同步可能带来的低频扰动，实际工程中，应从设计上考虑各变流器间的载波同步方案。

4 试验验证

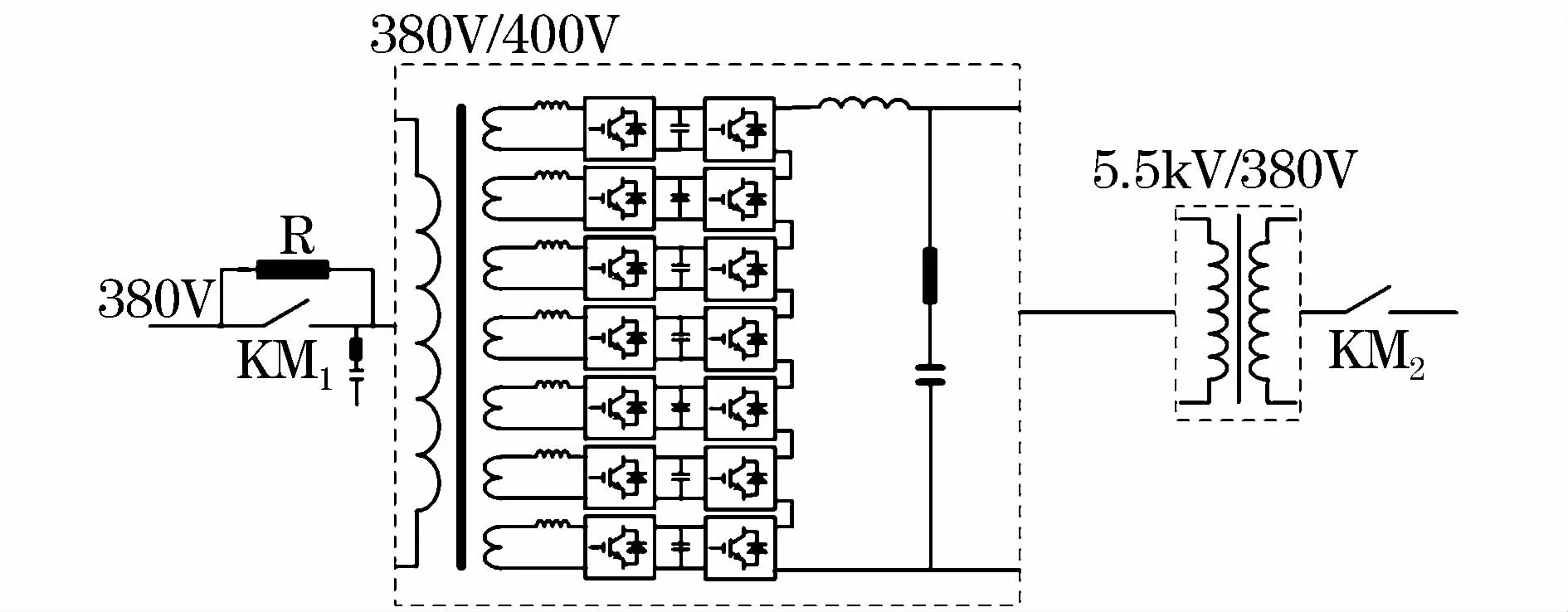
图5 1MVA智能电子负载Fig.5 Topological graph of intelligent electronic load

试验样机为一台1 MVA智能电子负载，其拓扑如图5所示。为了得到更大的容量及更高的等效开关频率，整流侧采用了单相多绕组变压器＋变流器结构，逆变侧采用单相级联技术。智能电子负载由独立的三个单相构成，输入三角形连接，输出星形连接。智能电子负载实物见图6，关键参数见表1。

图6 智能电子负载Fig.6 Pictures of the intelligent electronic load

表1 主要设备参数Tab.1 Major parameter of the intelligent electrinic load

（1）载波相位相同

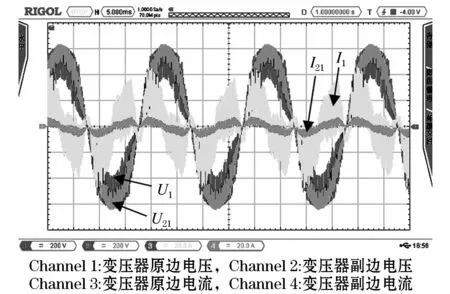
图7 载波同相位且空载时变压器原副边电压电流Fig.7 Original vice edge voltage and current of transformer as the carriers with the same-phase and no-load

以A相为例，当整流侧载波相位相同π／n时，多绕组变压器原副边电流、电压波形如图7所示，此时逆变侧未启动。从图中可以看出，变压器副边电流I21主要包含高频谐波，低频部分几乎为零；原边电流I1主要包含基波和3次谐波的励磁电流以及高频谐波，变压器接近饱和，电流存在一定畸变。I1峰-峰值为88 A，I21峰-峰值为11.2 A，考虑变压器380／400的变比，I1大概是I21的7倍（与副边并联单元数相同）。从而验证了，当变流器载波同相时，原边电流的高频谐波是副边各个单元电流高频谐波的线性叠加。

（2）载波移相 π／n

采用本文分析的载波移相π／n时，同时考虑空载和有功负载的情况，U1、I1和 I21的波形如图 8所示。

其中，图8（a）为逆变侧未启动，整流侧空载的情况。可以看出I21中主要包含高频谐波，而由于载波移相，I1中的高频部分相互抵消，波形效果明显变好。图8（b）为逆变侧启动带有功负载的情况。I21的波形为基波叠加高频谐波部分，但是I1中高频部分较少，相比较于载波未移相时，电流光滑且正弦度良好。表明采用载波移相后π／n，I1中的高频部分被部分抵消，与本文的理论分析一致。

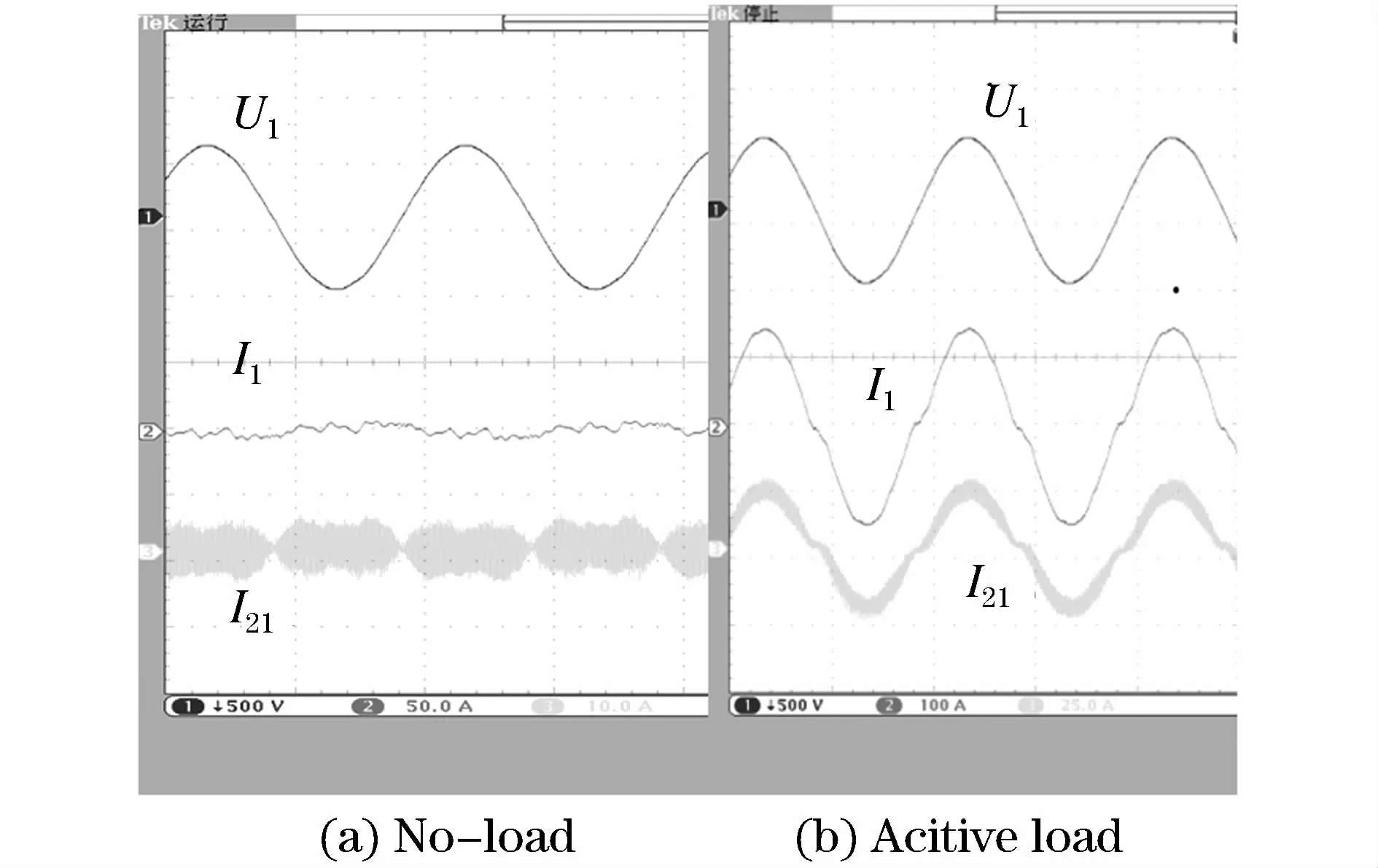
图8 载波移相π／n时空载和有功负载实验Fig.8 Experiment of no-load and active power load when carriers are phase-shifted byπ／n

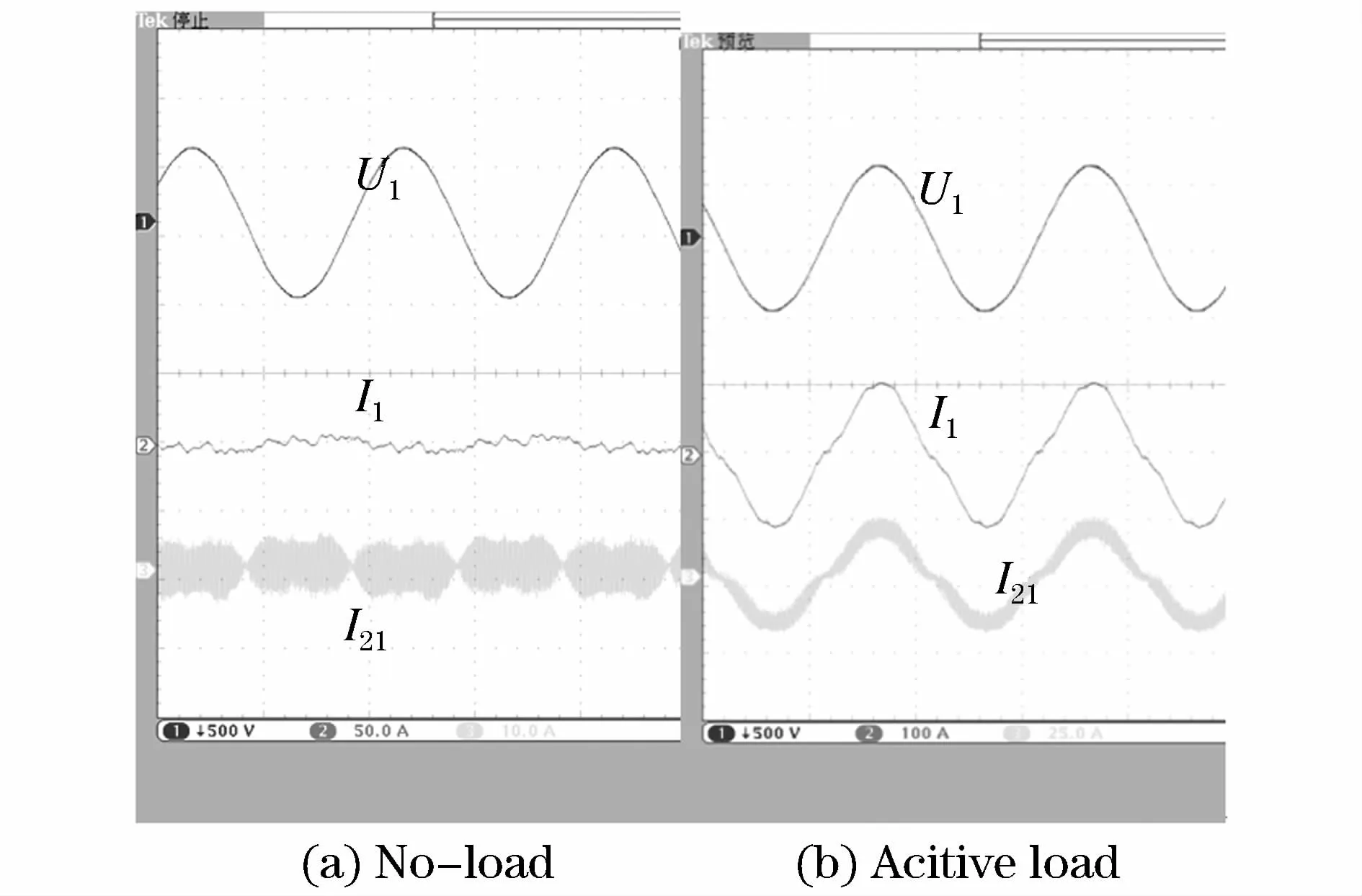
图9 载波移相2π／n时空载和有功负载实验Fig.9 Experiment of no-load and active power load when carriers are phase-shifted by 2π／n

（3）载波移相2π／n

同时考虑空载和输出有功电流的情况，U1、I1和I21的波形如图9所示。由于λ＝2与7互质，谐波抵消情况应该和λ＝1相同。从实验波形中可以看出，和载波移相π／n相比未有变化。类似的，当λ＝3、4、5、6时亦没有变化，限于篇幅这里就不一一展开。

5 结束语

文章以单相多绕组变压器＋单相H桥变流器结构为例，对其高频谐波进行了理论分析和抑制策略研究。采用多绕组变压器射线形模型，从理论上解释了载波移相法抑制消除高频谐波的原理并给出了最佳移相规律，即各单元载波互差π／n。通过实验证明，载波移相π／n后，原边电流有明显改善；且证明了载波移相2π／n时效果相同。文章的结论在单相情况下分析并验证，其结论在三相系统中同样适用。

然而，在采用载波移相后，变压器副边电流高频部分增大，增大了变压器损耗，如何解决这一问题将是未来的研究方向。