数据挖掘在电能质量监测数据分析中的应用*
2017-12-20林顺富谢潮汤波潘爱强周健
林顺富,谢潮,汤波,潘爱强,周健
(1.上海电力学院电气工程学院,上海200090;2.国网上海电力公司电力科学研究院,上海200437)
0 引 言
随着我国经济的持续发展,电力用户对电能需求日益增加的同时,对电能质量的要求也越来越高。电力公司在电网各电压等级监测点安装了大量电能质量监测设备,构成了电能质量监测系统,系统长期不间断的监测形成电能质量海量数据[1-2]。
近年来,人们逐渐意识到电能质量海量监测数据本身承载着大量涉及系统和设备运行状态的有用信息。其应用价值已远远超出传统电能质量所关注的范围,对故障的定位、系统异常预警、运行状态检测等具有重要意义[3-5]。在电能质量海量数据分析时,传统统计学方法已不能满足需求。数据挖掘技术能从海量数据中寻找出有用的隐含信息,逐渐被应用于电能质量数据分析中[6-8]。
文献[9]概述了数据挖掘技术在电能质量分析中的应用并指出了其广阔的应用前景,但由于多项电能质量扰动问题的存在导致目前仍然处于初级阶段。文献[10]采用基于最小信息长度的聚类算法检测监测点可能出现的异常电能质量事件,根据得到的集群特征通过分类技术推断未来监测点的电能质量事件。文献[11]采用支持向量机(SVM)有效识别大范围内参数任意变化的各类电能质量扰动,而且具备识别精确率高,实时性能好,对噪声干扰不敏感等优点。文献[12]结合模糊数学的有关知识,建立了电能质量模糊评价模型,并根据二级模糊综合评判方法结合多组实测数据进行评判分析,证实了所提方法的有效性和合理性。文献[13]提出的适用于配电网的优选组合预测模型,根据南方电网某变电站电能质量监测数据预测电能质量的未来状况,相比单个预测模型具有误差小、预测精度高等优点。
当前国内外研究多数将数据挖掘技术应用于电能质量扰动事件识别[14]、指标预测等方面,而对于电能质量指标受环境、气象等因素影响的规律,以及电能质量指标之间内在关联性的研究较少。本文从实际应用出发,提出一种基于数据挖掘技术处理电能质量数据的分析体系,并应用于国内某城市电网电能质量监测数据分析中,采用数据清理、数据集成、聚类分析和相关性分析等技术,分析了不同电能质量指标之间的相关性以及气温对电能指标的影响。
1 基于数据挖掘的电能质量数据分析体系
基于数据挖掘的电能质量数据分析体系主要包括数据库创建、数据挖掘分析及应用分析。本文构建的基于数据挖掘的电能质量数据分析体系结构图如图1所示。
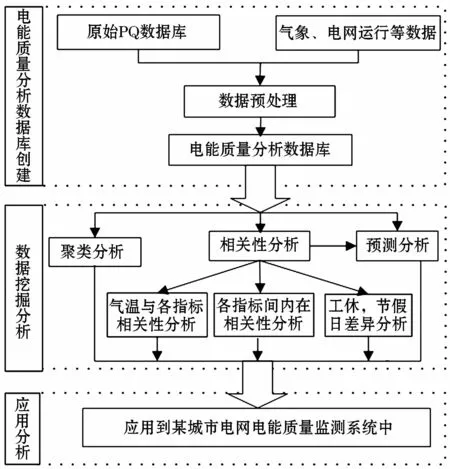
图1 基于数据挖掘的电能质量数据分析体系结构图Fig.1 Structure diagram of power quality data analysis system based on data mining
电能质量分析数据库除包括电能质量监测数据外,还包括电网运行的气象数据、电网操作数据等。由于相关数据量纲、存储格式存在差异,并且受电网运行状态及外部相关因素的影响,在进行数据分析前须进行数据集成、离群点检测、填补缺失值等预处理。数据集成可将不同来源数据进行科学合理的综合处理,因此首先将电能质量监测系统与气象监测系统不用数据库中的数据进行集成,形成一致性的数据模型,然后进行离群点检测与缺失值填补。数据挖掘技术是处理海量数据的有效工具。电能质量数据挖掘主要包括数据的聚类分析、相关性分析及预测分析等。根据最大化类内相似性与最小化类间相似性的原则把一个数据对象划分成子集的过程称为聚类。相关性分析指对具有相关性的变量元素进行分析以衡量变量因素之间的相关密切程度。通过相关性分析研究不同电能质量指标之间相关性、气温对电能指标的影响以及工休差异性分析具有重要意义。预测分析则是指根据现有的电能质量指标预测未来的趋势,为电网的运行提供有价值的参考。
2 电能质量数据预处理
电能质量监测网的海量数据大部分通过安装在监测点的复杂传感器进行采集,进而传输到终端系统内。在数据转换与通信的各个环节都有可能受到干扰,导致数据缺失或大量异常点的出现,影响数据的精度和可靠性。数据预处理主要是保证数据具有准确性、完整性与一致性三个要素。本文用到的预处理方法主要包括数据集成、离群点检测与缺失数据处理。
2.1 离群点检测
离群点是指与其他数据集不一致的数据。直观的说离群点是一个对象,它属于小的偏远簇,或者不属于任何簇[6]。本文采用聚类方法寻找数据集中可能存在的离群点,并对其进行处理。
对于每个指标c,可以根据该指标与最近簇中心的距离,给予该指标一个离群点判定系数。如果到指标c的最近中心为x,则c与x之间的欧氏距离为dist(c,x),中心x与指派到x的指标之间的平均距离为lx。采用比值 dist(c,x)/lx衡量 dist(c,x)与平均距离的差异程度,超出阈值范围内的视为离群点。
2.2 缺失数据处理
对于缺失数据主要采取基于相似性的递推方法,主要包括短时相似性、日相似性及月相似性数据递推等,具体处理方法如下。
(1)假设缺失数据在1小时之内,短时间内数据变化不是太大,取该指标前两个小时内的数据进行修正后填补缺失值;
(2)假设缺失数据在1小时与1天之间,取与该天同类型的日期进行填补。具体为:若缺失数据所在日期为工作日,取前两个工作日相同时刻的平均值作为填补数据。若缺失数据所在日期为非工作日,取前一周非工作日的平均值作为填补数据;
(3)假设缺失数据大于1天,取同一季节下一个月相同的日期进行填补。若缺失数据大于1个月,无论采取何种处理方法都对结果影响较大。则舍弃缺失严重数据,采用相对完整的数据进行处理分析。
3 电能质量数据挖掘分析
3.1 聚类分析
Mac Queen于1967年首次提出了 K-means算法。该算法的核心思想是找出K个聚类中心c1,c2,c3…ck,使得每一个数据点和与其最近的聚类中心的平方距离和最小化。
文中进行聚类的指标主要包括电压偏差、频率偏差、三相不平衡、长时短时闪变、总谐波畸变率、有功功率等。以有功功率与气温为例开展聚类分析。具体步骤如下:
(1)设原始数据集合 X={x1,x2,…,xi,…,xn},其中xi为d维的向量。首先设定聚类个数K,从集合X中任意选定k个向量作为各个类的中心ck(k=1,2,...,K);
(2)计算集合X中剩余向量到各中心ck的欧氏距离,根据距离最近原则将剩余向量分配到与其相异度最低的类,形成K个簇B={bk,k=1,2,…,K}。每个簇bk代表一个类。计算各类聚类中心ck到各元素的距离平方和J(bk):

(3)计算各类样本到其所在类别聚类中心ck总距离平方和J(B),直至最小。

其中若 xi∈bk,rki=1;若 xi∉bk,rki=0。取每个类中所有向量的平均值作为该类新的聚类中心;
(4)转到步骤(2),直到聚类中心不发生改变且J(B)小于设定阈值,聚类结束。
考虑聚类的收敛速度以及数据量级差别过大对算法的敏感性,需要在聚类前对原始数据进行归一化处理。首先确定历史PQ数据的最大值xmax与最小值 xmin,利用式(3)将数据映射到区间[0,1]。

然后利用式(4)将归一化数据换算为真实值。
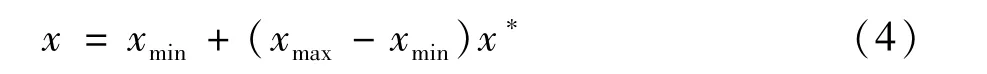
引入 Davies-Bouldin指数[15](DBI)来评估聚类结果好坏。DBI是计算类内距离之和与类外距离之比,根据最小DBI值选择最优聚类k值。对某监测点2012年全年有功功率与气温归一化后数据开展聚类分析,得到不同k值对应的DBI值,如表1所示,当k=4时,DBI值最小,聚类效果最佳。

表1 有功功率-气温聚类有效性评估Tab.1 Cluster validity index evaluation of active power and temperature
图2代表有功功率与气温在k=4时的聚类效果图。分层现象反映出负荷中存在气温敏感负荷和气温非敏感负荷,当气温高于25℃或低于15℃时气温敏感负荷开始投入运行。

图2 有功功率-气温聚类图Fig.2 Clustering results of active power versus temperature
3.2 相关性分析
相关性分析指对具有相关性的变量元素进行分析以衡量变量因素之间的相关密切程度。通过相关性分析研究不同电能质量指标之间的相关性以及温度对电能指标的影响具有重要意义。用来描述变量之间线性相关密切程度的Pearson积距相关系[6]ρxy定义为:
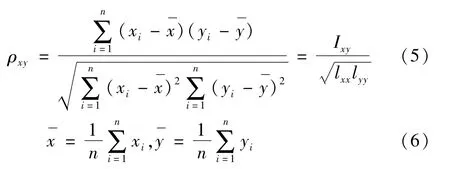
式中x,y是两个连续变量;lxy是x与y的离均差交叉乘积和;lxx,lyy分别是x和y的离均差平方和;n为指标序列的样本个数;xi,yi为计算区间段的2个指标时间序列第i个数值,为指标在区间段内的平均值;若 ρxy<0,表明两个指标为负相关;若 ρxy>0,表明两个指标为正相关;|ρxy|越接近0说明相关性越小,|ρxy|越接近1说明相关性越大。
以长时、短时电压闪变值与气温为例开展相关性分析。根据某监测点2012年全年的闪变值与气温数据,对各气温对应的所有闪变值取均值,从而得到图3所示各气温与相对应闪变值的关系曲线图。长时电压闪变与短时电压闪变变化趋势基本相同,两者Pearson积距相关系数为0.781 3,相关性较强;短时闪变值大部分小于长时闪变值;闪变在2℃~6℃及25℃~32℃时闪变水平最高,在其他气温相对较低且平稳,这间接反映出上述气温时段中温控负荷的频繁变化导致闪变发生。
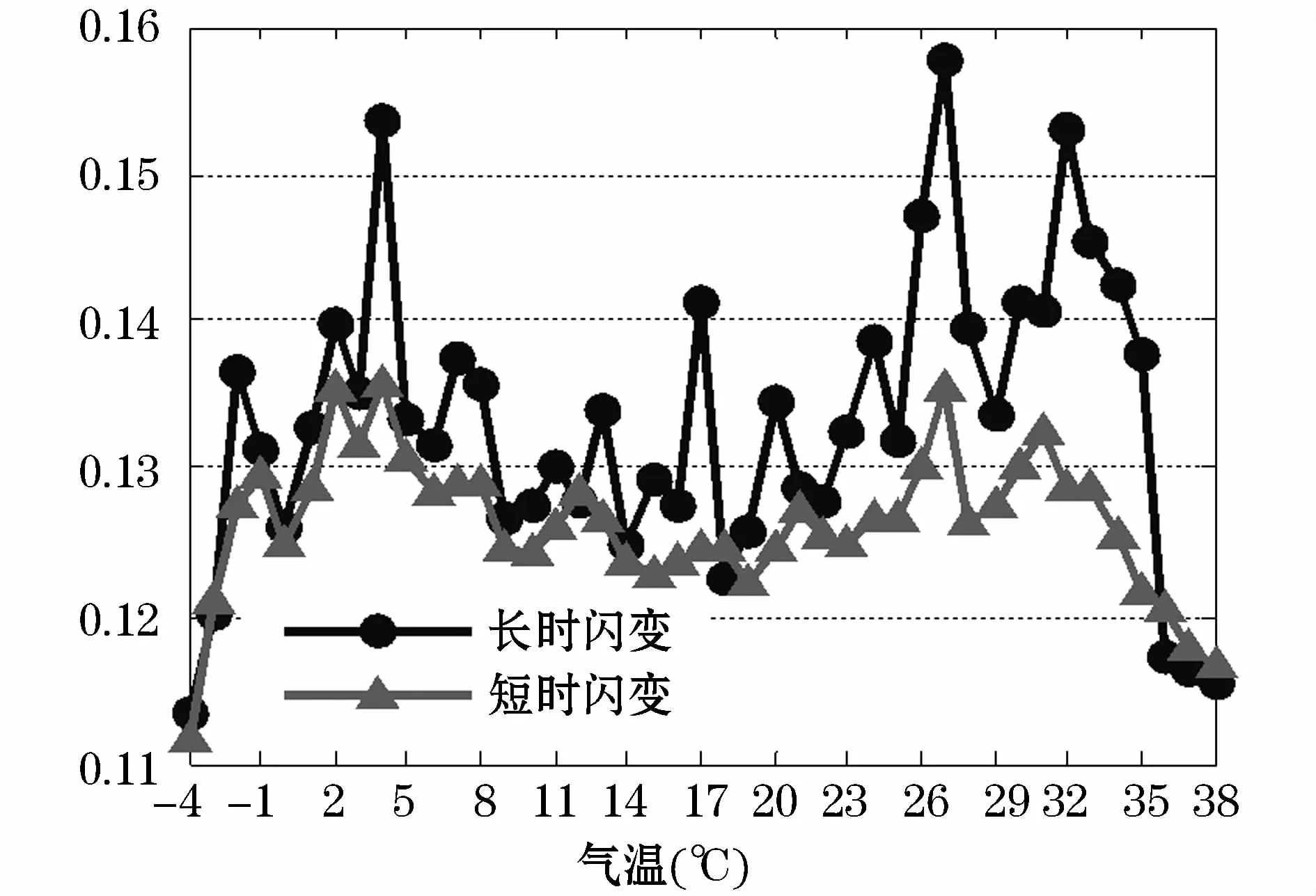
图3 闪变与气温关系曲线图Fig.3 Relation curves of flicker and temperature
4 应用案例分析
本文采用国内某城市电网电能质量监测系统数据,数据管理软件采用PQView。数据库中不仅包含各监测点电压、电流、频率、有功、无功与视在功率,还包括三相不平衡、谐波、间谐波、闪变与暂态事件等。除了实时数据外,也包含最大值、最小值、平均值以及95%概率值等各类统计数据。PQView软件数据采样间隔为5 min,气象监测部门提供的数据精确到1 h。
以有功功率与温度为例开展相关性分析。选择夏季、冬季代表月份作为研究目标。根据某监测点2012年8月份与12月份的工作日数据,做出8月份日最大负荷与最高气温的关系图见图4。做出12月份日最大负荷与最低气温的关系图见图5。日最高、平均、最低气温与日最大有功功率的Pearson积距相关系数见表2。由关系图与相关系数的分析可知,夏季时日最大负荷与最高气温的线性相关度较强,并且为正相关,即最高气温越高,有功消耗越大。相关性强是由于温度较高时大量降温负荷的开启。冬季时(12月份)日最大有功功率与最低气温的线性相关度较强,是负相关,即最低气温越低,有功消耗越大,主要原因是大量取暖负荷的工作。
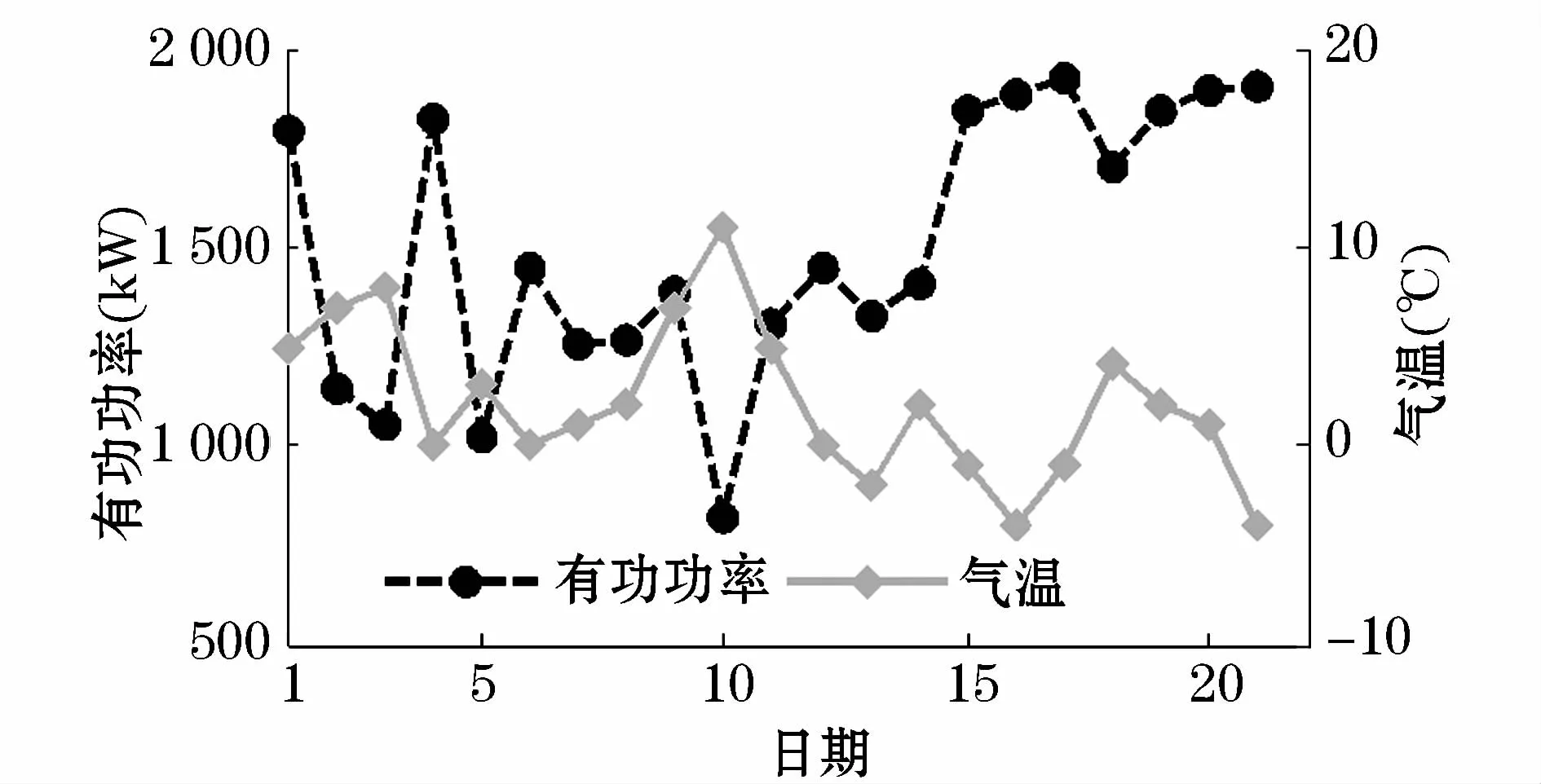
图5 2012年12月日最大负荷与日最低气温关系图Fig.5 Relation curves of the maximum daily load and the minimum daily temperature(December 2012)
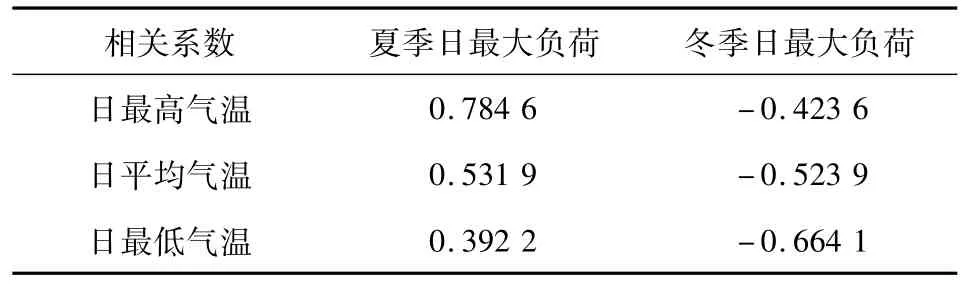
表2 日最大负荷与气温相关系数Tab.2 Correlation coefficient of daily peak load and temperature
预测每天的峰值负荷对电网调度有重要意义,基于上述分析得出峰值负荷与气温有一定线性关系。取某监测点2012年日最高气温与最大负荷做散点图,工作日和周末采用不同标记以观察周工作模式。从图6可知绝大多数周末的日最大负荷远小于工作日最大负荷,夏季的日最大负荷要高于冬季。在气温20℃左右时日最大负荷最低,随着气温升高或降低,有功功率呈现线性递增关系。主要原因是最让人感觉舒适的气温在20℃左右,此时空调负荷最低。
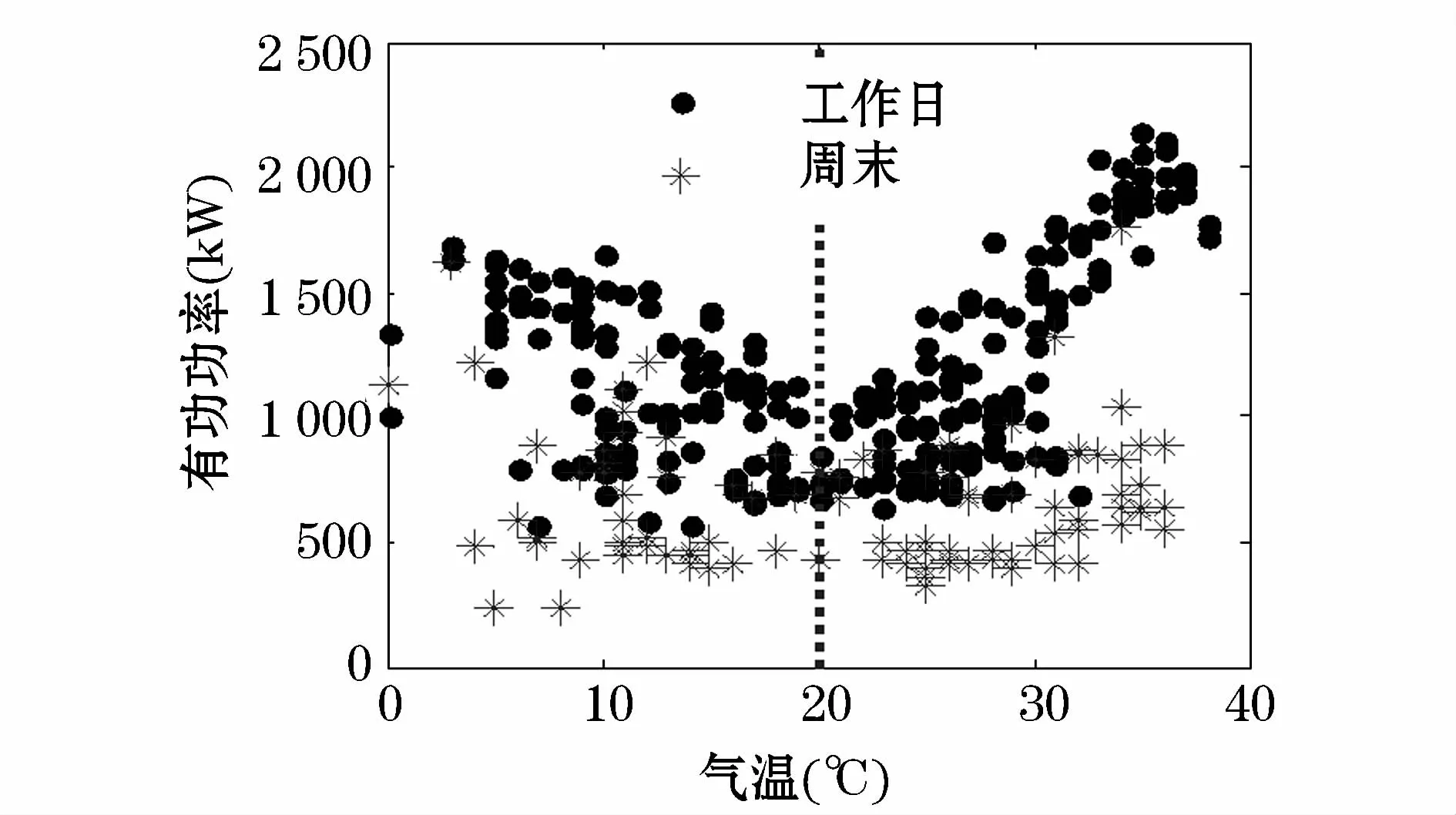
图6 2012年日最大负荷与日最高气温散点图Fig.6 Scatter diagram of the maximum daily load versus temperature in 2012
为了研究三相电压、电流不平衡度之间的相关性,采用某监测点2012年8月份三相不平衡度数据,取每小时最大值做散点图如图7所示。分析可知在一定时间内,随着三相电压不平衡度的增大三相电流不平衡度也会在一定程度上增大,两者呈正相关。可能的原因包括单相大容量负荷在电气位置上分布不合理,大容量负荷开启的瞬间也会同时影响三相电压、电流不平衡度。
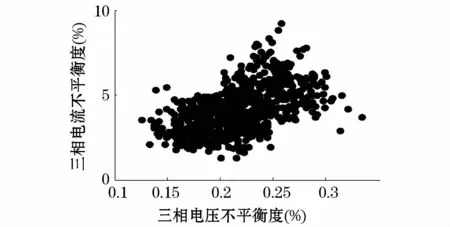
图7 三相电压-电流不平衡度散点图Fig.7 Scatter diagram of three-phase voltage balance factor and three-phase current unbalance factor
大部分谐波由非线性设备产生,但对于环境、气象等因素与谐波的相关性研究较少。根据某监测点电压总谐波畸变率与各次谐波电压的大小,做出电压总谐波畸变率THDu、5次谐波电压含有率与气温的散点图见图8。电压总谐波畸变率与5次谐波电压含有率受气温的影响较为明显,在20℃左右时两者处于最低水平,随着气温升高或降低呈现上升趋势。主要原因是气温高于25℃或低于10℃时,空调等非线性负荷启动且占比较大,产生谐波进入电网。
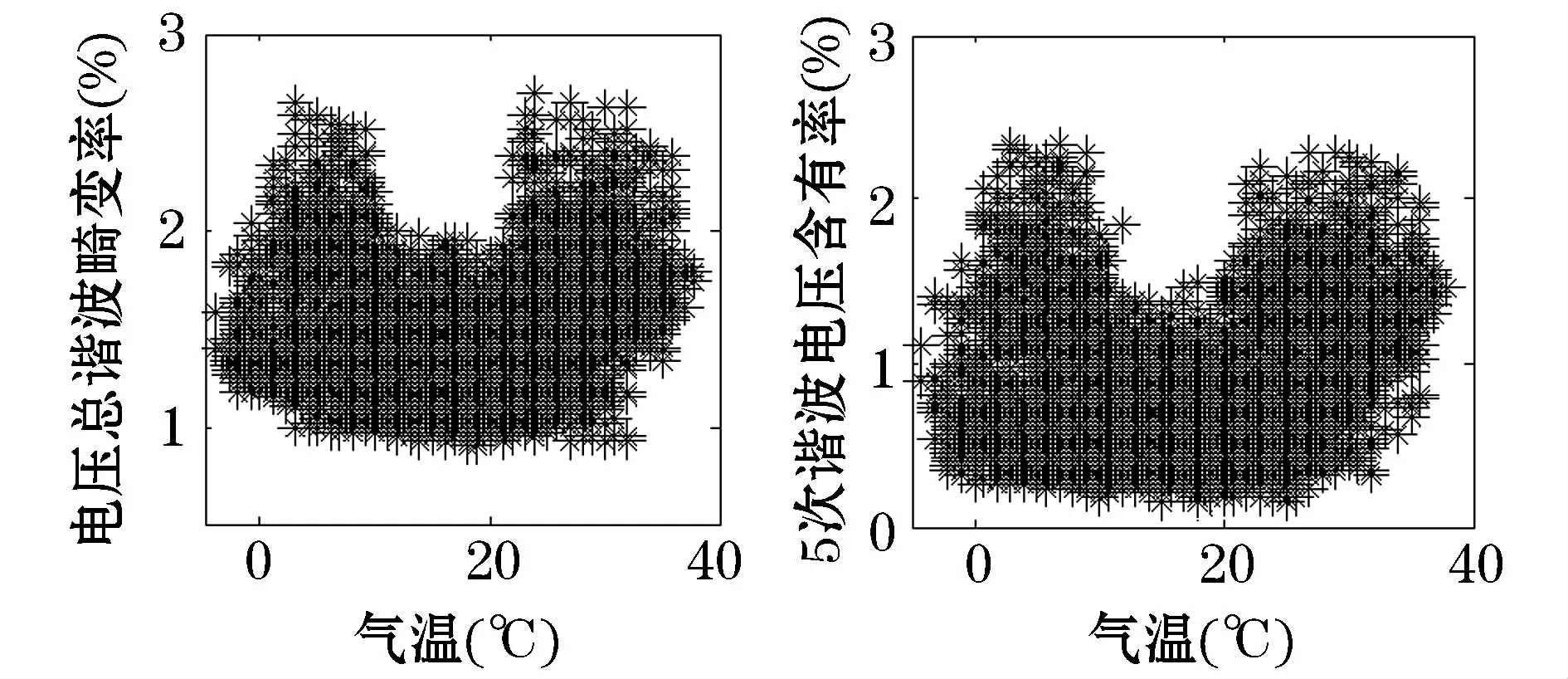
图8 电压总谐波畸变率,5次谐波电压含有率与气温散点图Fig.8 Scatter diagram of voltage THD,5th voltage harmonic ratio versus temperature
图9表示某监测点电流总谐波畸变率THDi与负载电流有效值的散点图。可以看出在负荷较小时谐波畸变反而更严重,图中拟合曲线反应了电流总谐波畸变率随负载电流的变化趋势,可根据回归方程与负载电流粗略预测THDi的大小。
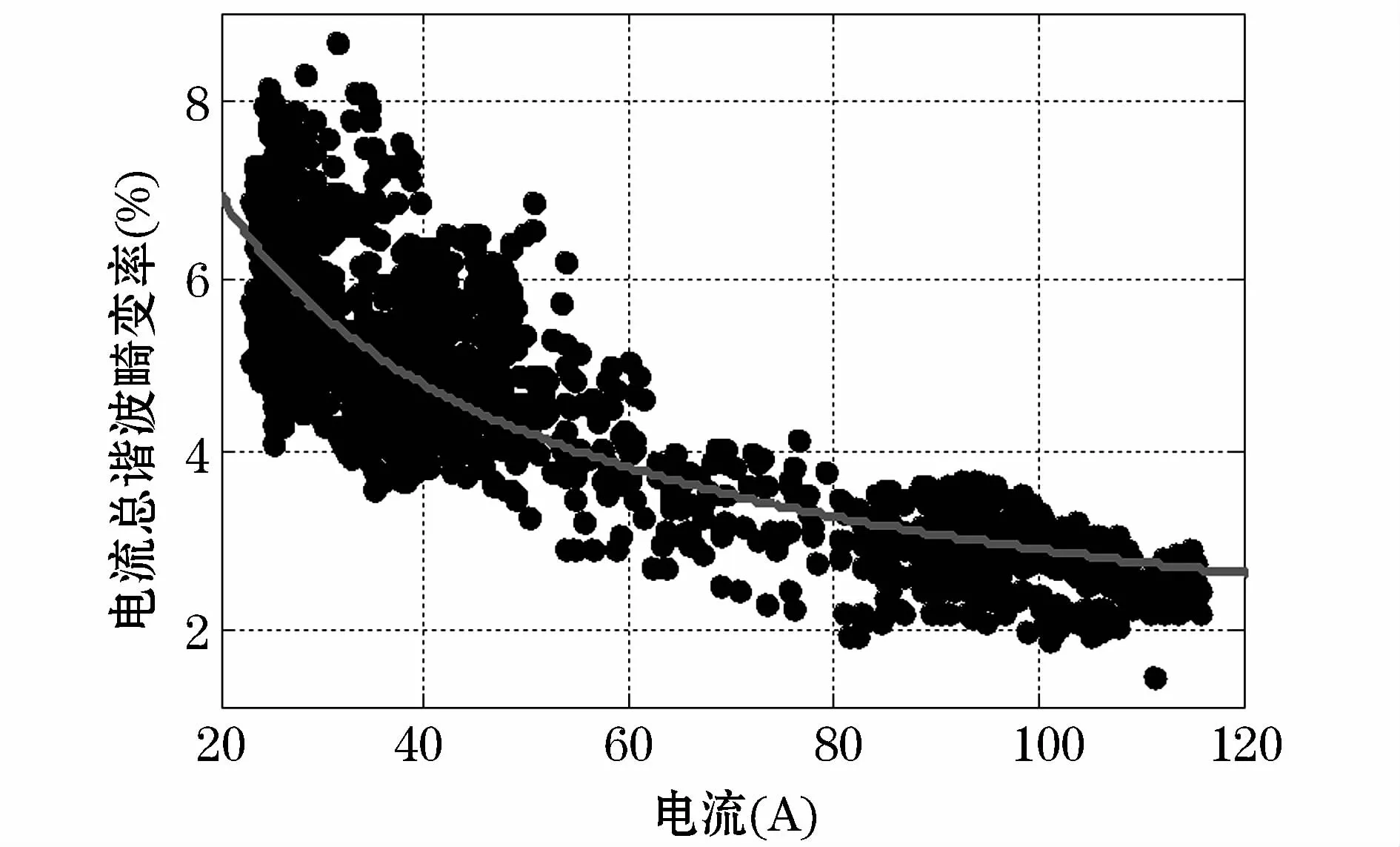
图9 电流总谐波畸变率-电流关系图Fig.9 Scatter diagram of current THD and current RMS
5 结束语
提出了一种基于数据挖掘技术处理电能质量数据的分析体系,并应用于国内某城市电网电能质量监测网数据分析中,采用数据清理、数据集成、聚类分析和相关性分析等技术,分析了不同电能质量指标之间的相关性以及气温对电能指标的影响,获得了有意义的电能质量指标变化规律,为电网规划、调度和运行提供了有价值的参考。
