土壤电导率分层对地闪回击水平电场时空分布规律的影响

毕睿华

（南京工程学院，南京211167）

土壤电导率分层对地闪回击水平电场时空分布规律的影响

毕睿华

（南京工程学院，南京211167）

地闪回击产生的水平电场是架空输电线路产生雷电感应过电压的主要原因，目前国内很多学者对电磁场时间变化规律进行了分析，但是针对电磁场空间分布特征还没有过多的研究。采用了二维时域有限差分法（2D FDTD），研究土壤电导率水平分层情况下地闪回击水平电场时空分布特征。结果表明：1）在均匀有耗大地情况下，水平电场分布从回击通道开始以光的传播速度沿近似半球面向远处传播时，随着时间的增加，水平电场的分布也相应增加。在近地面处，水平电场极性与周围其他空间处的水平电场相反，且随着传播距离的增大，该区域范围也在扩大。相比于均匀有耗大地的情况，理想大地情况下水平电场传播显得比较简单；2）土壤分层情况下的水平电场也出现了水平电场极性反转的现象。当上层土壤电导率大于下层时（Case1），其极性反转区域随传播距离整个极性反转区域形状呈现出上升沿较陡、下降沿较缓的特征。

水平电场；有限电导率；水平分层；二维时域有限差分；空间分布

0 引言

在电力系统防雷中，架空输电线由于线路长、分布广等特点更易受到雷击，输电线路会由于雷击线路产生直击雷过电压，但直击雷发生的概率远小于非直击雷，所以雷电对架空输电线的危害主要来源于雷击线路附近产生的感应过电压。研究雷电感应过电压的产生和发展规律，为架空输电线防雷设计提供参考依据，需要深入探讨雷电回击产生的电磁场，在分析地闪回击电磁场在架空线上产生感应过电压时，最常用的传输线耦合模型是Agrawal模型[1]，而地闪回击产生的水平电场在其中扮演了重要角色。

在计算雷击通道周围空间电磁场方面，精确算法需要引入Sommerfeld卷积积分[2]，该方法解决了地闪回击电磁场沿有限电导率大地传播的问题，但计算复杂、收敛缓慢，需消耗大量时间，效率很低，对Sommerfeld卷积积分进行近似处理后，出现了许多便于计算雷电水平电场的近似算法[3]。目前广泛采用的主要是Cooray-Rubinstein（C-R）近似算法[4-11]，它可以计算大地电导率均匀与非均匀分布情况下的水平电场，且在计算近距离水平电场时具有很好的精度。随着计算机技术的发展，数字模拟算法得到广泛应用，主要有矩量法（MOM）和时域有限差分法（FDTD），其中时域有限差分（FDTD）法在求解电磁场问题上具有广泛的适用性，自1966年K.S.Yee[12]提出以来，该方法得到迅速发展和应用，并被应用于雷电研究[13]。FDTD在计算闪电回击通道近距离处的电磁场时更具有优势，因其不涉及复杂的微积分运算，程序代码易于实现。杨春山、周璧华等[14]采用二维FDTD法，分析了距离闪电通道附近1 km以内的雷电电磁场。Mimouni等[15]将FDTD方法应用到地面以下电磁场的计算。杨波、周璧华等[16]提出了采用二维时域有限差分法（FDTD）法，计算了LEMP在地下不同深度的分布。张其林、郄秀书等[17]根据表面波理论，分析讨论了地面有限电导率对雷电电磁波传播的影响。张其林、李东帅等[18]进一步拓展了C-R近似算法，计算了不同粗糙地表面条件以及海陆混合路径下的雷电水平电场。

目前，大多数对雷电电磁场的数值模拟一般把大地假设为理想导体或者等效为地参数取固定值的均匀大地情况，而实际情况中的大地为有限电导率而且具有分层结构，不同的地质条件下土壤电导率分布不均匀，另外，比如雷暴发生时的降水也会影响土壤湿度，进而会改变土壤电导率，大地有限电导率及其分层情况可能对地闪回击电磁场的传播有很大影响。笔者将对土壤电导率水平分层情况进行模拟，采用二维时域有限差分方法计算地闪回击水平电场，分析不同土壤电导率分层条件对地闪回击水平电场传播的影响，所得结论对进一步分析和计算雷电电磁场在架空输电线上的耦合问题具有重要意义。

1 地闪回击电磁场计算模型

计算地闪回击通道周围产生的电磁场，本文假设回击电流通道垂直于大地，每段通道高度处均可用工程计算中的电流元代替，即随时间变化的电偶极子，在计算空间中某位置的电磁场值时，即相当于对地闪回击通道上的所有电偶极子在该位置处产生的电磁场值的叠加。本文采用二维时域有限差分法进行计算。

时域有限差分法（FDTD）核心思想是把Maxwell旋度方程转化为差分形式，模拟其时域响应，即将Maxwell时域微分方程进行中心离散，通过时间和空间上的交替迭代来求解空间中所有格点的电磁场值。本文采用二维轴对称柱坐标系下麦克斯韦旋度方程差分格式，包含水平磁场Hφ，垂直电场Ez，水平电场Er3个分量，其时间推进计算公式[19]为

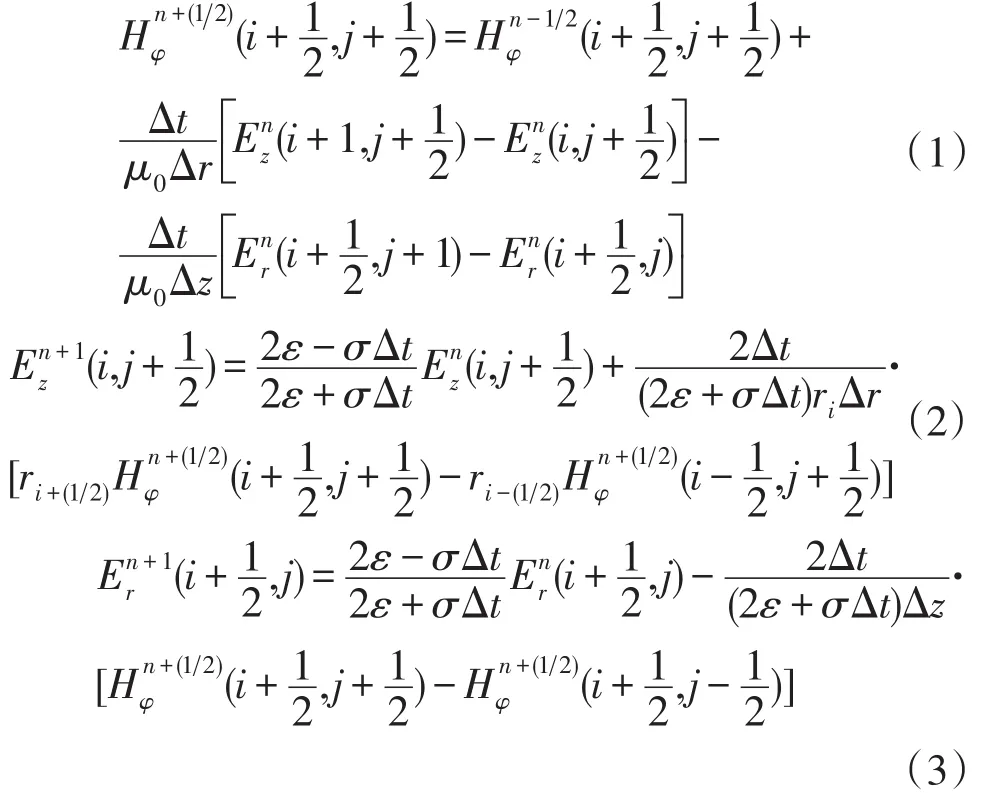
为了保证时间步长Δt和空间步长Δr、Δz满足Courant稳定性条件，避免随着计算时间步的增加，计算结果也无限制增加，笔者选取的离散网格空间步长Δr=Δz=1m，时间步长

为模拟开域的电磁波传播过程，使得电磁波在FDTD计算区域边界上不产生明显反射，需要设置吸收边界条件，笔者采用了一阶Mur吸收边界[20]。在本文中，计算空间足够大，即便电磁波有反射也不会对所研究的时间内观测点所在位置产生影响，因此一阶Mur吸收边界可以满足本文的研究需要。

笔者采用Rakov和Dulzon提出的MTLL模型[21-22]。它表示回击电流以速度v向上传播，在传输过程中电流幅值随高度线性衰减。MTLL模型的回击通道中电流公式如下：

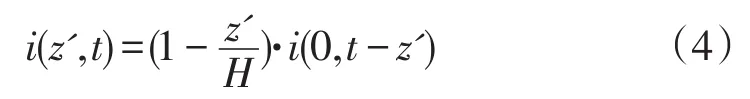
式中：z'表示通道中回击电流波所传播到的高度；H为闪电通道高度，本节中取电流通道高H=7.5 km；v为回击电流波的传播速度，等于地闪回击速度，取表示t时刻的回击电流波。图1给出了本文所使用的二维计算空间模型示意图。

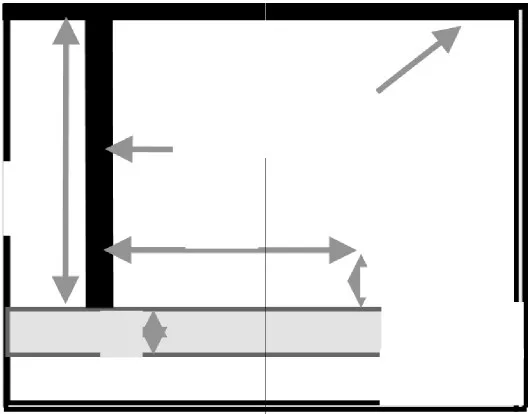
图1 二维FDTD计算雷电流电磁场的空间模型Fig.1 Two-dimensional FDTD calculation of the electromagnetic model of lightning current

计算空间建立在二维轴对称柱坐标系下，图1所示的半空间大小r×z=2 000 m×2 000 m，以Δr=Δz=1m二维网格作剖分，时间步长Δt=Δr/（2c）满足Courant稳定性条件。地面土层水平设置为两层，每层厚度均为L。假设地闪回击通道垂直于地面，高度H设置为7 500 m。计算空间边界条件采用一阶Mur吸收边界。

2 雷电电磁场传播空间分布特征

2.1 均匀有耗地面和假设理想大地的对比

基于雷电工程模型，可以求出电磁波沿着无限大良导体地面传播的情况，良导体电导率约为107S/m，而实际地面土壤电导率的典型值为10-1～10-3S/m，且变化很大。大地土壤电导率的典型值与假设理想大地（良导体）的电导率相差108～1010个量级，所以有必要研究有限电导率对雷电电磁波在传播过程中的衰减作用，大地电导率参数设置见表1。

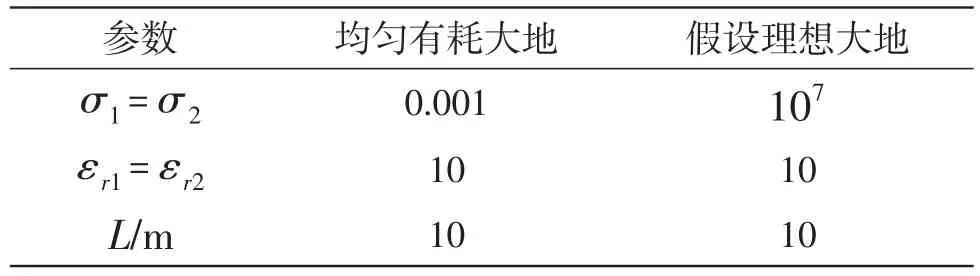
表1 均匀大地情况下电导率设置Table 1 Conductivity setting for uniform earth conditions

表1中，L为土层厚度，上下层厚度均设置为10 m，无分层情况时，土壤厚度即为20 m。通过计算得到计算区域内水平电场的时空分布，见图2。

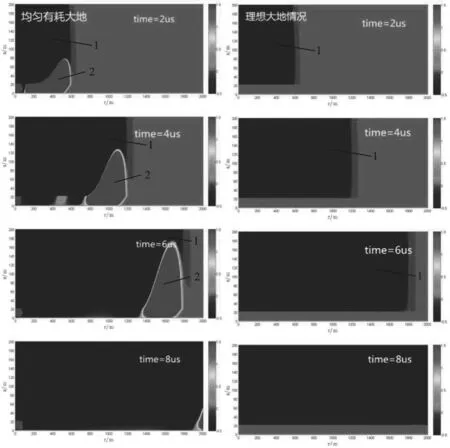
图2 均匀有耗大地和理想大地情况水平电场时空分布图Fig.2 Spatial and temporal distribution of horizontal electric fields with uniformly dissipated earth and ideal earth

分别选取了电磁波传播后不同时刻（选择2、4、6、8 μs）的水平电场的空间分布，选择显示的主要为近地面处，高度从0～200 m处，其中20 m以下为地层土壤部分，水平距离为整个径向距离2 000 m。图2分别显示了均匀有耗大地和理想大地两种情况下的水平电场时空分布。根据图2计算结果显示，在均匀有耗大地情况下，回击产生后，水平电场分布从回击通道开始以光的传播速度沿近似半球面向远处传播时，随着时间的增加，水平电场的分布也相应增加（1区域）。在近地面处，存在着一个呈波形特征的区域，该区域水平电场极性与周围其他空间处的水平电场相反（2区域），且随着传播距离的增大，该区域范围也在扩大。除了地面以上空间内存在水平电场的传播，可以看到地面以下也存在水平电场，即高度在0～20 m的空间内，而且可以看到电磁波在土壤中的反射等传播情况。此外，通过观察8 us时刻的水平电场分布图，电磁波在计算空间的吸收边界处并没有产生明显的反射，这也证明了本文所采用的一阶Mur吸收边界是满足计算需要的。

相比均匀有耗大地的情况，理想大地情况下，水平电场传播显得比较简单。在电磁波未传播到的区域，以及电导率为良导体的理想大地部分均无水平电场的存在，水平电场只存在于地面以上所播到的空间。而且，不存在水平电场极性反转的区域，即水平电场表现为单极性，这与均匀有耗大地的情况不同。

2.2 电导率水平分层情况对回击水平电场传播的影响

考虑到实际土壤情况，由于地质构造、土壤含水量等因素影响，实际土壤有别于2.1，讨论的单层有耗土壤模型或假设理想大地，土壤结构必然存在分层，土壤电导率的不均匀分布也将对雷电电磁波的传播产生影响。在此笔者对土壤电导率水平分层情况下地闪回击产生的水平电场进行了计算和分析。

为了便于探讨不同土壤电导率分层情况对地闪回击水平电场传播的影响，本文选取0.1 S/m与0.001 S/m两个土壤电导率典型值进行土壤结构参数化建模，相对介电常数均设置为10 F/m。采用第二节介绍的上下两层的水平分层计算模型，相关参数有空气中ε0=8.85×10-12F/m，μ0=4π×10-7H/m，σ0=0 S/m，L为土层厚度，上下两层土壤厚度均设置为10 m。土壤水平分层有两种情况（Case1、Case2），第一种分层情况：上层土壤电导率大于下层（Case1），第二种分层情况：上层土壤电导率小于下层（Case2），为比较电导率对水平电场传播的影响，因此两种情况下相对介电常数取值均为10。具体大地电导率参数设置见表2。

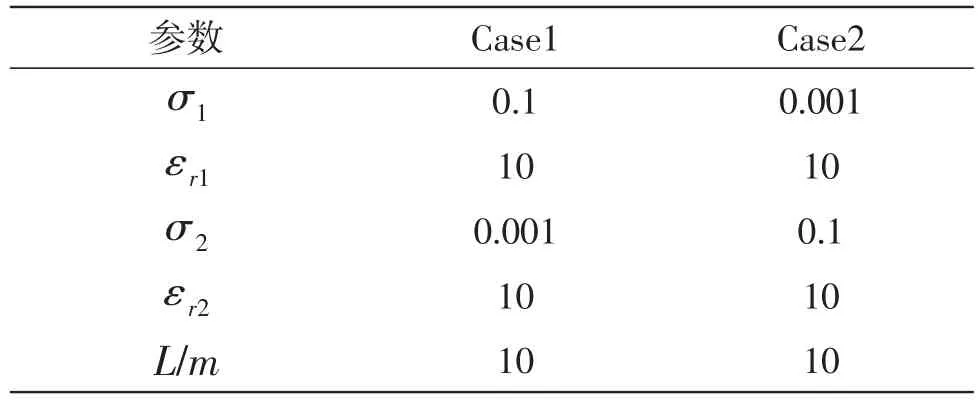
表2 分层土壤情况下地参数设置Table 2 Parameter setting for stratified soil conditions

图3给出了分层土壤计算模型在地闪回击产生后不同时刻的水平电场空间分布图。选取4个时刻t=2、4、6、8μs，分别对应传播距离600、1 200、1 800、2 400 m，选择显示的空间为地面以上的近地面处，即高度在20～200 m之间，（其中0～20 m高度之间为土壤层），水平距离覆盖整个径向距离2 000 m。

由图3可发现，两种土壤分层情况下的水平电场时空分布与图2中均匀有耗地面时的情况类似，均出现了水平电场极性反转的现象（如图中1区域），但不完全相同。首先在于负极性水平电场区域的范围大小不同，在Case1中（上层土壤电导率大于下层），其产生的水平电场极性反转区域明显小于Case2的情况。另外，水平电场极性反转区域形状也有所差异，在上层土壤电导率大于下层时（Case1），其极性反转区域随传播距离整个极性反转区域形状呈现出上升沿较陡、下降沿较缓的特征，这与所选雷电回击通道基电流波形类似，而在上层土壤电导率小于下层时（Case2），反转区域显示出更高的上升沿陡度和较高的下降沿陡度，而且后续极性反转区域部分并不连续，所以在近地面不同水平距离上，其水平电场的传播波形将表现出震荡的特征。

3 结论

雷电回击水平电场是架空输电线路产生雷电感应过电压的主要因素，选用双Heidler函数和MTLL模型作为地闪回击通道基电流和回击模型，利用二维时域有限差分法计算并分析了地闪回击产生的水平电场的传播规律，并分析了有限土壤电导率及其水平分层情况对水平电场传播空间分布特征。具体结论如下：

1）在均匀有耗大地情况下，回击产生后，水平电场分布从回击通道开始以光的传播速度沿近似半球面向远处传播时，随着时间的增加，水平电场的分布也相应增加。在近地面处，存在一个呈波形特征的区域，该区域水平电场极性与周围其他空间处的水平电场相反，且随着传播距离的增大，该区域范围也在扩大。相比于均匀有耗大地的情况，理想大地情况下水平电场传播显得比较简单。

图3 Case1和Case2情况水平电场时空分布图Fig.3 Case1 and Case2 situation Horizontal electric field spatiotemporal distribution

2）两种土壤分层情况下的水平电场出现了水平电场极性反转的现象。在方案1中产生的水平电场极性反转区域明显小于方案2的情况。另外，在上层土壤电导率大于下层时（Case1），其极性反转区域随传播距离整个极性反转区域形状呈现出上升沿较陡、下降沿较缓的特征。

[1]AGRAWAL A，GURBAXANI S.Transient response of multiconductor transmission lines excited by a nonuniform electromagnetic field[C]//Antennas and Propagation Soci⁃ety International Symposium.IEEE，1980:432-435.

[2]SOMMERFELD A N.Über die ausbreitung der wellen in der drahtlosen.[J].Annalen Der Physik，2006，333（4）:665-736.

[3]NORTON K A.The propagation of radio waves over the surface of the earth and in the upper atmosphere[J].1936，25（9）:1203-1236.

[4]BREMMER H.The extension of sommerfeld's formula for the propagation of radio waves over a flat earth，to differ⁃ent conductivities of the soil[J].Physica，1954，20（1）:441-460.

[5]KING R J.Electromagnetic wave propagation over a con⁃stant impedance plane[J].Radio Science，1969，4（3）:255-268.

[6]BANNISTER P R.Extension of quasi-static range finitely conducting Earth-image theory techniques to other ranges[J].IEEE Transactions on Antennas& Propagation，1978，26（3）:507-508.

[7]COORAY V.Horizontal fields generated by return strokes[J].Radio Science，2016，27（4）:529-537.

[8]RUBINSTEIN M.An approximate formula for the calcula⁃tion of the horizontal electric field from lighning at close，intermediate and long ranges[J].IEEE Trans Electromagn Compat，1996，38（3）:531-535.

[9]SHOORY A，MOINI R，SADEGHI S H H，et al.Analy⁃sis of lightning electromagnetic fields in the vicinity of lossy ground[J].IEEE Trans Electromagn Compat，2005，47（1）:131-145.

[10]杨春山，周璧华，陈彬.计算地闪回击电流水平场的混合法[J].微波学报，2003，19（2）:81-84.YANG Chunshan，ZHOU Bihua，CHEN Bin.A hybrid method for calculating the horizontal field of lightning re⁃turn current[J].Journal of Microwave Society，2003，19（2）:81-84.

[11]COORAY V. Some considerations on the‘cooray-rubin⁃stein’formulation used in deriving the horizontal electric field of lightning return strokes over finitely conducting ground[J].IEEE Trans Electromag.Compat，2002，44（4）:560-566.

[12]YEE K S.Numerical solution of initial boundary value problem involving Maxwell's equations in isotropic media[J].IEEE Trans on Antennas and Propagation，1966，14（4）:302-307.

[13]HU W，CUMMER S A.A new FDTD model for lightning generated EM wave simulation[C]//Antennas and Propaga⁃tion Society International Symposium.IEEE，2002:1061-1064.

[14]YANG C，ZHOU B.Calculation methods of electromag⁃netic fields very close to lightning[J].IEEE Trans Electro⁃magn Compat，2004，46（1）:133-141.

[15]MIMOUNI A，DELFINO F，PROCOPIO R，et al.On the computation of underground electromagnetic fields generat⁃ed by lightning:a comparison between different approaches[C]//Power Tech，2007 IEEE Lausanne.IEEE，2007:772-777.

[16]任合明，周璧华.地闪电磁脉冲对近地电缆外导体的耦合研究[J].电波科学学报，2006，21（5）:750-755.REN Heming，ZHOU Bihua.Lightning electromagnetic pulse on the coupling of[J].Cable Radio Science Journal，2006，21（5）:750-755.

[17]张其林，郄秀书.地面有限电导率对雷电电磁波传播的影响[J].高电压技术，2008，36（9）：23-25.ZHANG Qilin，QIE Xiushu.Ground finite conductivity ef⁃fect on lightning electromagnetic wave propagation[J].High Voltage Engineering，2008，36（9）:23-25.

[18]ZHANG Qilin，LI Dongshuai，TANG Xiao et al. Light⁃ning-radiated horizontal electric field over a rough-and ocean-land mixed propagation path[J].IEEE，2013，55（4）:733-738.

[19]YANG C，ZHOU B.Calculation methods of electromagnet⁃ic fields very close to lightning[J].IEEE Transactions on Electromagnetic Compatibility，2004，46（1）:133-141.

[20]葛德彪，闰玉波.电磁波时域有限差分方法[M].西安:西安电了科技大学出版社，2010:37-49.

[21]LIN Y T，UMAN M A，STLER R B.Lightning return stroke model[J].Journal of Geophysical Research Oceans，1980，85（C3）:1571-1583.

[22]RAKOV V A，DULZON.A modified transmission line model for lightning return stroke field calculations[C].In Proc，9th on Electromagnetic Compatibility，Zutich，Swit⁃zerland.1991:229-235.

Influence of Soil Conductivity Stratification on Temporal and Spatial Distribution of Ground Flashover Return Strike Horizontal Electric Field

BI Ruihua
（Nanjing Institute of Technology，Nanjing 211167，China）

The horizontal electric field generated by lightning is the main reason for the overhead transmission line from lightning induced overvoltage，many domestic scholars on the variation of electro⁃magnetic field time are analyzed，but according to the electromagnetic field distribution characteristics of space is not too much research.In this paper，the two-dimensional finite difference time domain（2D）method is used to study the temporal and spatial distribution characteristics of the horizontal electric field of the lightning return stroke in the case of soil electrical conductivity stratification（FDTD）.The results show that:1）in the homogeneous earth under the condition of horizontal electric field distribution from the back channel begins with the speed of light propagation along the propagation distance for approximate hemisphere，as time increases，the distribution of the horizontal electric field is also increased.In the near surface，the horizontal electric field polarity is opposite to the horizontal electric field in the other space，and with the increase of the propagation distance，the range of the region is also expanding.Com⁃pared with the case where the earth is uniform，the propagation of horizontal electric field in the ideal ground is relatively simple;2）the horizontal electric field is reversed in the horizontal electric field under the condition of layered soil.When the conductivity of the upper soil layer is greater than that of the lower layer，the polarity reversal of the horizontal electric field is obviously less than that of the upper layer.

horizontal electric field；finite conductivity；horizontal stratification；two-dimensional time-domain finite difference；spatial distribution

10.16188/j.isa.1003-8337.2017.06.022

2017-06-29

毕睿华（1977—），男，硕士，讲师，主要研究方向：高电压技术，电力信息化技术。