船载外测数据的实时检择方法*

2017-12-20

电讯技术 2017年12期

(中国卫星海上测控部，江苏江阴 214431)

船载外测数据的实时检择方法*

吴金美**，侯亚威，李永刚，凌晓冬

(中国卫星海上测控部，江苏江阴 214431)

分析了航天测量船的任务特点和船载外测数据的野值特性，研究实时处理船载外测数据野值的检择方法。通过两套设备的外测数据信息横向比对消除船摇对数据检择的影响，建立了自适应权值和阈值的模型，给出了基于坐标转换和加权融合的分步式船载外测数据实时检择方法。实例数据验证结果表明所提方法可以实时有效地解决外测预处理阶段的野值检择问题。

航天测量船；外测数据；野值实时检择；加权融合

1 引言

航天测量船在对飞行器进行跟踪测量的数据处理过程中，必须对采样数据进行预处理，识别出其中的野值，这对改进后续数据处理的精度、提高数据处理质量相当重要。工程经验和统计理论告诉我们，即使是高精度的测量设备，由于多种偶然因素的综合影响或作用，采样数据集合往往包含1%～2%有时甚至10%～20%的数据严重偏离目标真值[1]。测量船在海上执行任务时，不可避免地受到风、浪、涌等因素的影响，使得船的位置和姿态处于时刻变化的过程中，固连在甲板上的外测设备获取的外测数据中除了含有与跟踪测量设备本身有关的测量误差外，还叠加了船体摇摆移动带来的测量误差，因此与陆基外测数据相比，船载外测数据的野值检择工作更为复杂和困难。

近年来，围绕野值的辨识和剔除已经有了相当多的研究[1-9]，但基本都是针对常见的陆基外测数据和事后数据处理来开展的，比如，陆基外测数据事后处理过程中的剔野常选用差分法、多项式逼近的最小二乘法、外推拟合法、多项式回归模型检验法、ARMA模型法检验法、稳健滤波的M估计法等[2]。不少学者在此基础上进一步改进，提出了等精度测量数据的逐点剔除法[3]、“稳健-似然比”检验法[1]、改进的卡尔曼滤波方法[4]、中值稳健估计法[5]、函数逼近和回归分析法[6]等，这些方法考虑的重点是剔野的成功率，对适用条件有一定的要求：有的对孤立型野值点效果显著，但对长时段的斑点数据就无能为力[7]；有的需要人工干预，不能实时快速处理；有的必须建立在新信息的基础上，难以适用于各种跟踪测量任务情况[8]；有的计算量比较大，不适合大容量数据的规模化处理；等等。

事实上，对于船载外测数据的实时检择过程，一方面要充分考虑船摇对数据的误差产生的影响，船载外测数据的野值与陆基测量数据的野值特性有所不同；另一方面与事后数据处理相比，实时数据处理强调算法简单、计算量小，而且每一时刻数据的处理只能依赖于之前的积累数据，没有办法对整个弧段大容量的数据进行分析判断，例如获取新息或者其他关键的统计值等。这两点就使得前面的野值辨识和处理方法无法在这一特定的环境中适用。

基于以上的背景，本文从分析航天测量船的任务特点和船载外测数据的野值特性入手，研究能够实时处理船载外测数据野值的检择方法。

2 船载外测数据的野值分析

飞行目标的跟踪测量中，设备状态不稳定甚至故障、人员操作失误、环境干扰等原因都会导致测量数据中个别或者成片的异常出现，即孤立型野值和斑点型野值。对于海上测量来说，环境更为多变，干扰时刻存在，孤立型和斑点型野值都有可能出现，如图1～2所示。

图1 测距数据中的孤立型野值Fig.1 Isolated outliers in distance measurement data

图2 测角数据中的斑点型野值Fig.2 Patchy outliers in angle measurement data

目前船载外测数据还是采用简单差分设定门限值的办法进行检择，对于图1这种突变较大的孤立型野值，即使宽松的门限值都能将野值剔除；而对于图2这种连续成片的野值，剔除的效果不好并且剔除后存在需要补点修复的问题。简单差分设定门限值的检择方法最大的问题是门限值的选取，过于宽松的门限值必然会造成漏点的情况，起不到检择的效果。每次任务的实时数据精度是有差异的，固定门限值或者任务前设定的估计值不能降低船摇的影响，不能准确体现出实时的数据精度。图1中测距数据因量级大所以受船摇影响很小，而图2就体现出船摇对俯仰角的影响了。

选取某次任务外测俯仰角数据并对它进行一阶差分，如图3～4，可以看出，随着船摇影响，数据曲线来回摆动，而且数据变化率也呈现出一种非单调变化的趋势。通过进一步分析可以得出[9-10]，船体不同方向的摇摆变化对方位俯仰距离的测量值的影响是不同的，距离受横摇的影响最明显，方位角受艏摇、横摇、纵摇3个方向尤其是艏摇的影响，俯仰角主要受横摇和纵摇的影响。但3个方向的船摇不完全是周期性的，难以用周期性的多项式来进行拟合和估计，因此在数据检择阶段无法通过建立数学模型估计出船摇再进行去除。测量船外测数据处理在预处理之后有专门的船摇修正过程，能够除去叠加在外测数据上的船摇的影响，但对原始数据的检择工作属于预处理过程，在测量坐标系就要进行，这就需要在获得船摇数据之前就能够充分利用已有的数据信息对存在的野值进行识别和剔除。

图3 俯仰角数据Fig.3 Elevation angle measurement data

图4 俯仰角数据的一阶差分Fig.4 The first order difference of elevation angle measurement data

通过对原始数据野值的分析可以得出，在预处理阶段，单一数据源的外测原始数据蕴含了船摇的信息无法用统计方法从外测数据中分离完成野值的检择。

测量船在执行任务时，每条船的参试设备往往不止一套，一般有两套或更多设备参与测量同一目标，安装在同一条船上的两套设备沿着船纵轴线分布，受到的船体摇摆的影响是基本一致的，因此，充分利用测量船的任务特点，采用两套设备的数据信息，进行横向比对的方式是完成检择的可行途径。

3 检择方法的数学模型

3.1 坐标系转换

如果设备1和设备2是位于同一条测量船上的两套外测设备，则设备1和设备2均在船的艏艉线上。不妨假设设备1靠近船艏，任意t时刻，设备1和设备2所测的方位角、俯仰角和距离为Ai(t)、Ei(t)、Ri(t),i=1,2，对于跟踪同一个目标的这两套设备来说，由于测量坐标系并不重合，因此就算没有任何测量误差，它们测到的数据也绝不会相同，尤其是某些特殊的弧段特殊的角度，差距更大。因此，对数据进行比对前，必须进行坐标系的转换。

首先，对两组测量数据从极坐标转换成直角坐标。若设设备1和设备2的直角坐标系下测量值为Xi(t)、Yi(t)、Zi(t)，i=1,2，则坐标转换公式为

(1)

其次，以设备1所在的测量系为基准，将设备2的测量系转化到基准坐标系。两个测量坐标系的原点为各自设备的方位轴与俯仰轴的焦点，X轴平行于船的艏艉线，并指向船艏，Y轴平行于方位轴方向，向上为正，z轴按右手法则确定。两个设备的测量坐标系的原点不重合所以需要进行坐标系的平移，而且因为有船体的变形存在导致三轴方向不平行，需要进行坐标系的旋转：从变形测量设备可以获得因船体变形引起的设备1和2之间存在的3个自由度变化角，设船体变形角欧拉矩阵为Bb。值得注意的是，虽然变形角是一个实测的变化值，如果引入测量值进行实时转化，可能会因为存在时延让数据预处理的实时性得不到满足，另一方面测量值有误差，反而会影响数据精度，考虑到变形数据的特殊性——平滑不会有突变，不会导致野值的增加或扩大，因此我们用固定变形角来参与计算，进行坐标系的转换。在后续的检择计算过程中，固定变形值不会影响数据检择的结果。

如果设备2的原点在基准坐标系里的坐标为X0、Y0、Z0，则设备2的测量值转换到基准坐标系中坐标值为

(2)

3.2 加权融合

设通过坐标转换后的两设备测量数据为Si(t)=(SXi(t),SYi(t),SZi(t))τ，i=1,2。若目标在基准坐标系下的飞行轨迹为S0(t)=(SX0(t),SY0(t),SZ0(t))τ，则Si(t)=S0(t)+K(t)+ei(t)+εi(t)。其中，K(t)是t时刻船摇带来的影响，ei(t)是设备本身的系统误差，εi(t)是零均值的随机误差。测量设备的系统误差大部分可以通过事前发现并消除，但如前所述，船摇的影响是无法消除的，两组测量值中都含有相同的船摇影响，可以利用两组数据中所体现的共同的主体“趋势”对各组数据进行检择。

对于多传感器的数据融合时的权值计算，文献[11]已经给出了最优的分配原则，与陆基传感器数据不同的是，船载外测数据包含了船摇影响，但注意到因为船摇对两设备的影响是相同的，事实上不论权值怎么定，加权后的融合数据中的船摇影响还是与两设备数据是一致的，并不会因为权值分配的不同而变化，因此船摇影响在加权融合时可以忽略，依据陆基传感器的分配原则来计算权值。

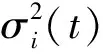
(3)

可以证明[11-12]融合数据的方差

(4)

也就是说利用最优的权值分配原则，即便加入了精度较差的设备数据源也有利于提高融合数据的精度，因为融合后的数据精度高于其中任何一个设备数据。

3.3 数据检择

(5)

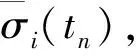
设

则

(6)

根据前面的分析可得到具体的分步式检择算法：

Step1 初始检择，设定初始精度值和阈值，第一点无条件接受，从第二点起，用与前一点的绝对差小于阈值进行检择，剔除野值直到积累m点后进入正常检择。

Step2 正常检择，根据前面m个数据的精度利用式(3)计算融合数据，并进行多项式拟合，计算第m点的精度估计值并根据式(5)对第m点的数据进行检择。若判定为野值，则进入修正检择。

值得注意的是，在此检择算法当中，实时计算加权融合的权值和检择的阈值，因此阈值和权值都是自适应的。

4 实例验证

例1：采用某次卫星入轨段的船载外测测角数据，雷达1和雷达2同时进行测量得到图5和图6，两设备受到相同的船摇影响，体现出大致相同的趋势，局部放大可见雷达1的测角数据在1 166 s有一个孤立型野值(如图7所示)，只是从整个任务段的数据量级中相形较小，隐藏在船摇的振荡里。

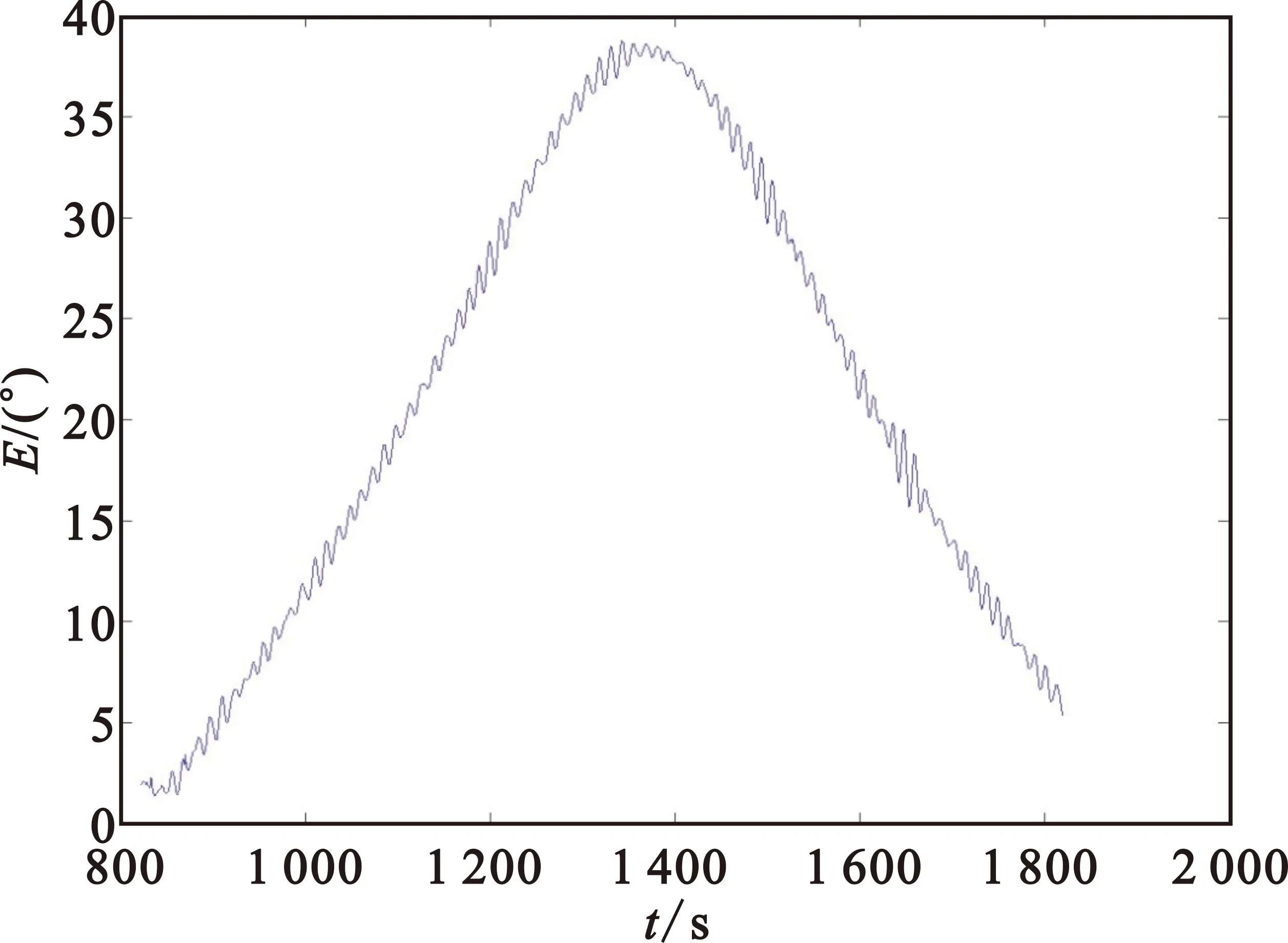
图5 雷达1全任务时段俯仰角数据Fig.5 Elevation angle measurement data from Radar 1 in the full task time

图6 雷达2全任务时段俯仰角数据Fig.6 Elevation angle measurement data from Radar 2 in the full task time

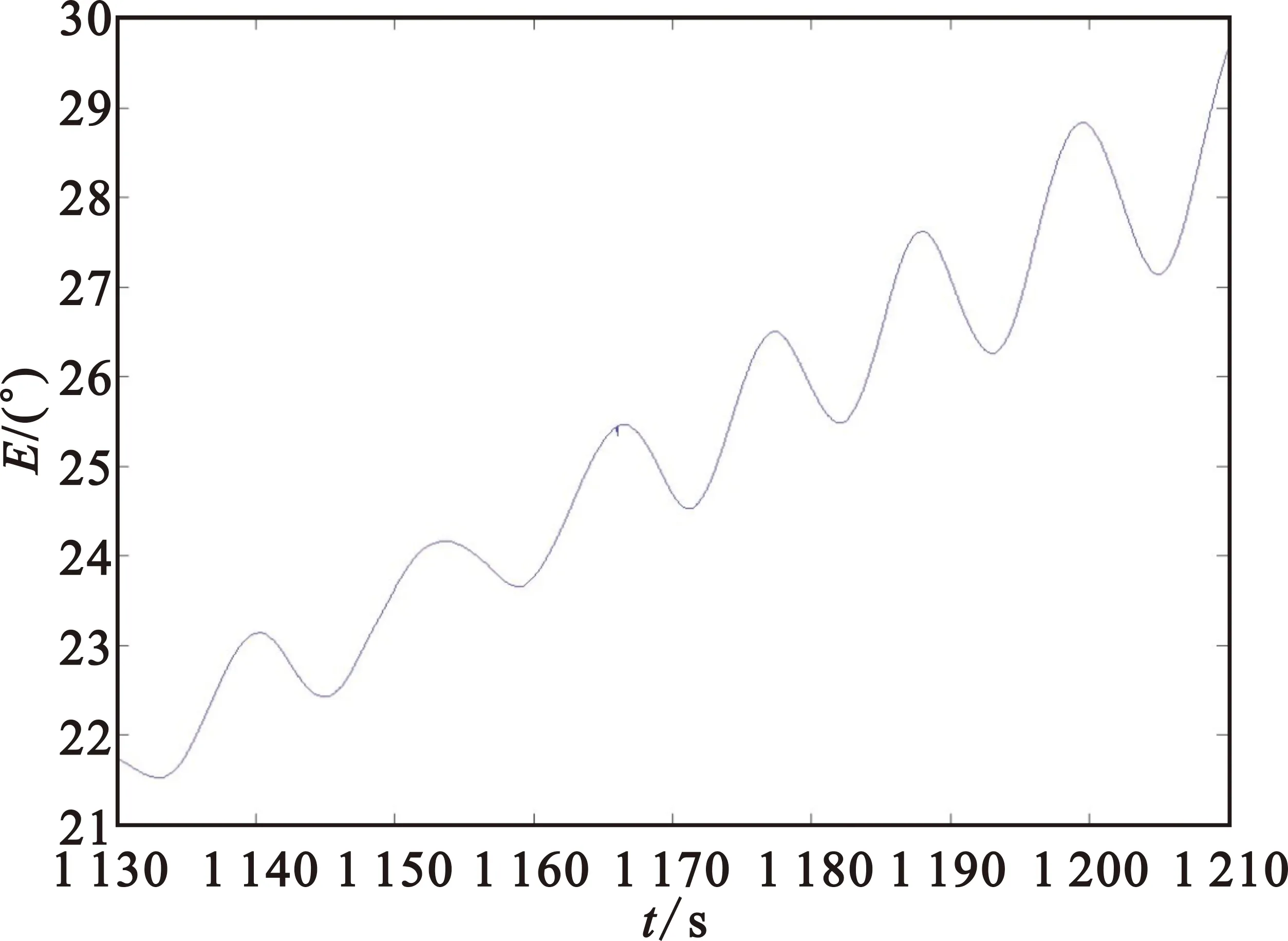
图7 雷达1俯仰角局部放大Fig.7 Partially zoomed figure of elevation angle measurement data from Radar 1

对雷达1测角数据进行简单差分设定门限法进行处理。用任务前给出的测元变化率来确定门限值进行检择，从检择后的差分图(图8)可以看到，由于门限值过于宽松，造成了漏警的现象。事实上因为初始段设备跟踪摆动较大加上船摇的影响，这在雷达2数据中也有体现，造成的第859 s数据差分也比较大，但这属于正常值，所以即便门限值足够小能够滤去野值，则相应地也会除去第859 s的正常值，造成虚警。

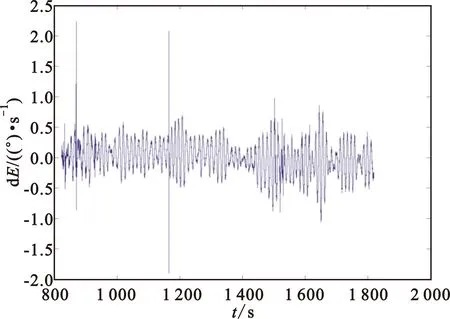
图8 雷达1俯仰角差分Fig.8 The first order difference of elevation angle measurement data from Radar 1

采用基于坐标转换和加权融合的分步式船载外测数据实时检择方法进行处理，得到正常的雷达1测角数据，并且可以看到第859 s的合理的实时测角数据也得到了保留,如图9所示。

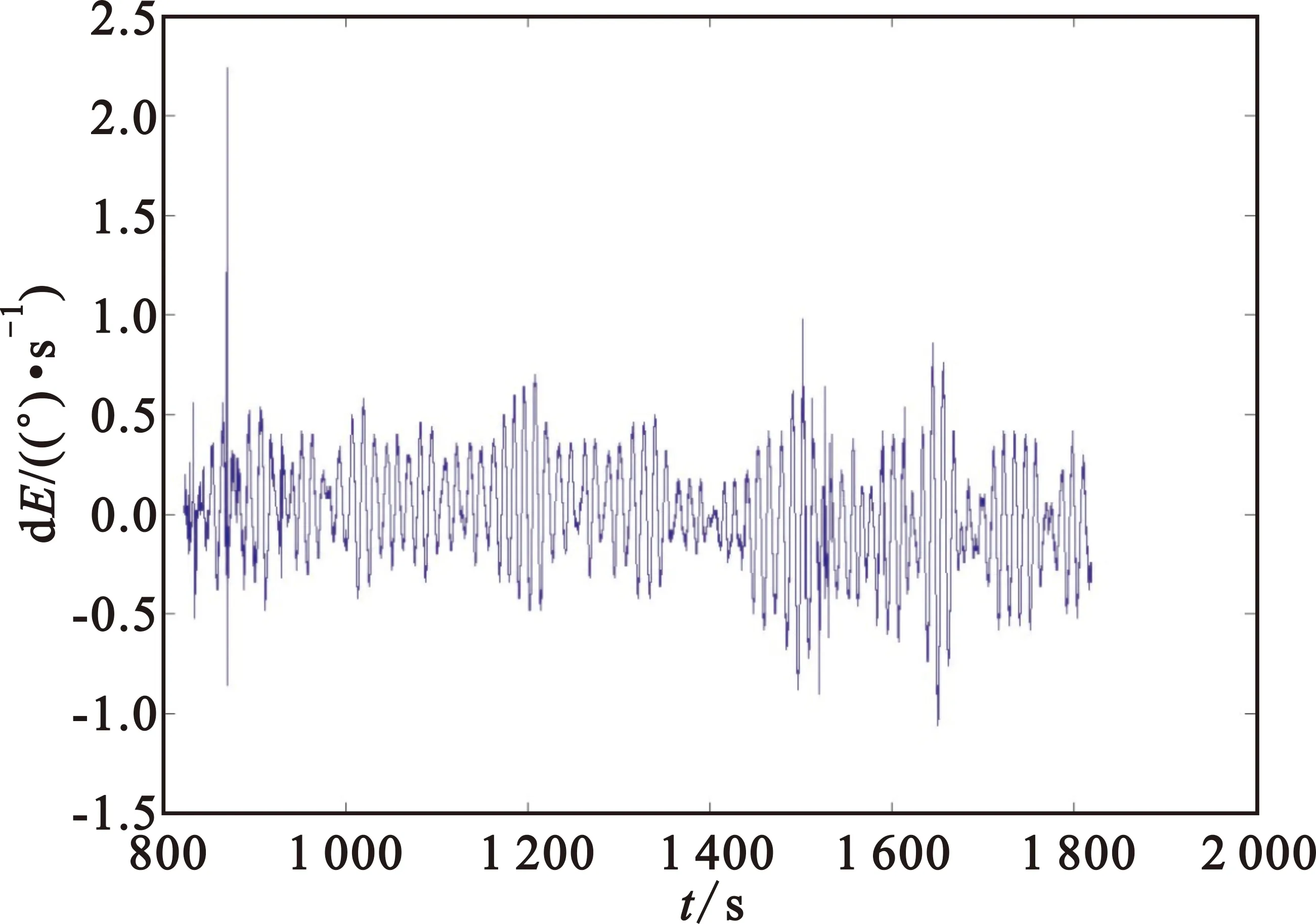
图9 检择后的雷达1俯仰角数据Fig.9 Elevation angle measurement data after detection from Radar 1

例2：采用某次卫星入轨段的测角数据，从第4 500点开始选择连续250点，在原始雷达2测量数据上加入固定常值进行模拟斑点型野值，对比同时段的雷达1测角数据,如图10～11所示。

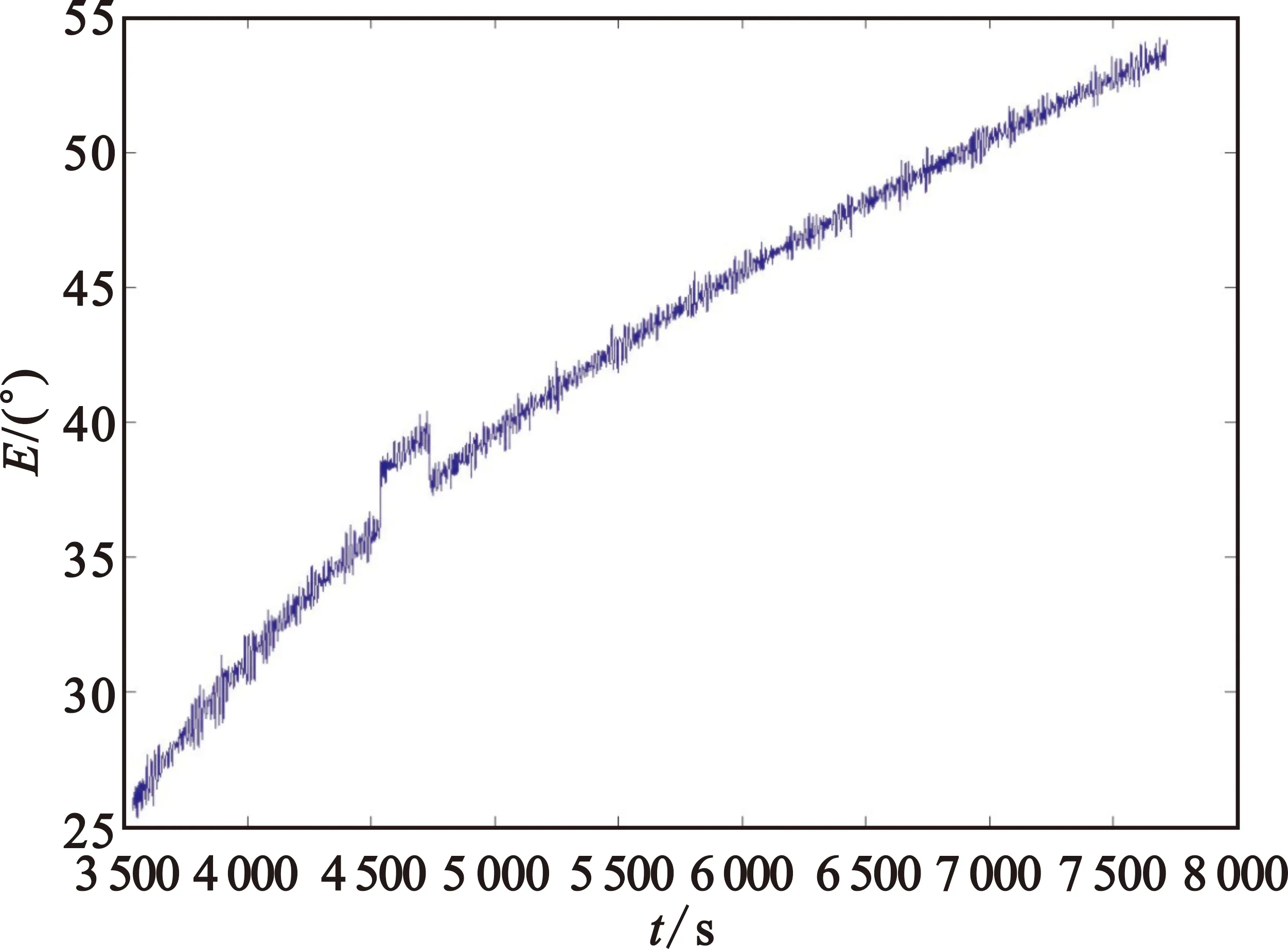
图10 雷达2俯仰角数据Fig.10 Elevation angle measurement data from Radar 2

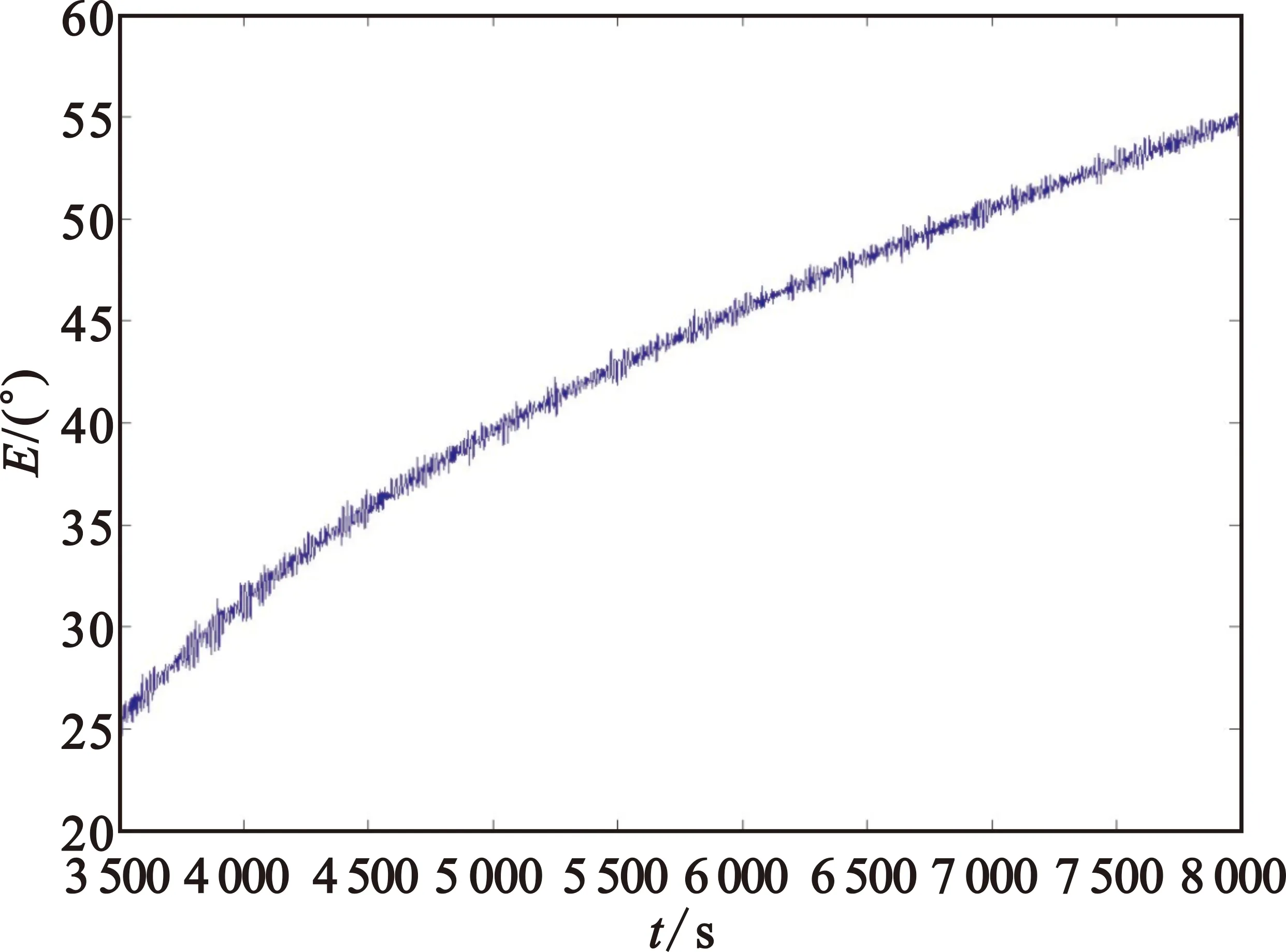
图11 雷达1俯仰角数据Fig.11 Elevation angle measurement data from Radar 1

对于这种斑点型野值，由于斑点长度较长而内部数据稳定差分比较小，简单差分设定门限法在连续识别4点标记为野值并处理数据后重新初始检择，默认接受第一点，这样就导致检择后的数据与之前相比只处理了4点，并没有对斑点做更多的处理，与原始数据并无明显差异。检择后的差分图如图12所示，斑点仍然存在，两端的差分值仍然很大。

图12 雷达2俯仰角差分图Fig.12 The first order difference of elevation angle measurement data from Radar 2

采用基于坐标转换和加权融合的分步式船载外测数据实时检择方法进行处理，结果如图13～14所示。因为充分利用了对比的雷达1数据，从结果可以看出，基本上将雷达2数据的斑点进行了修复，补点的效果比较理想。

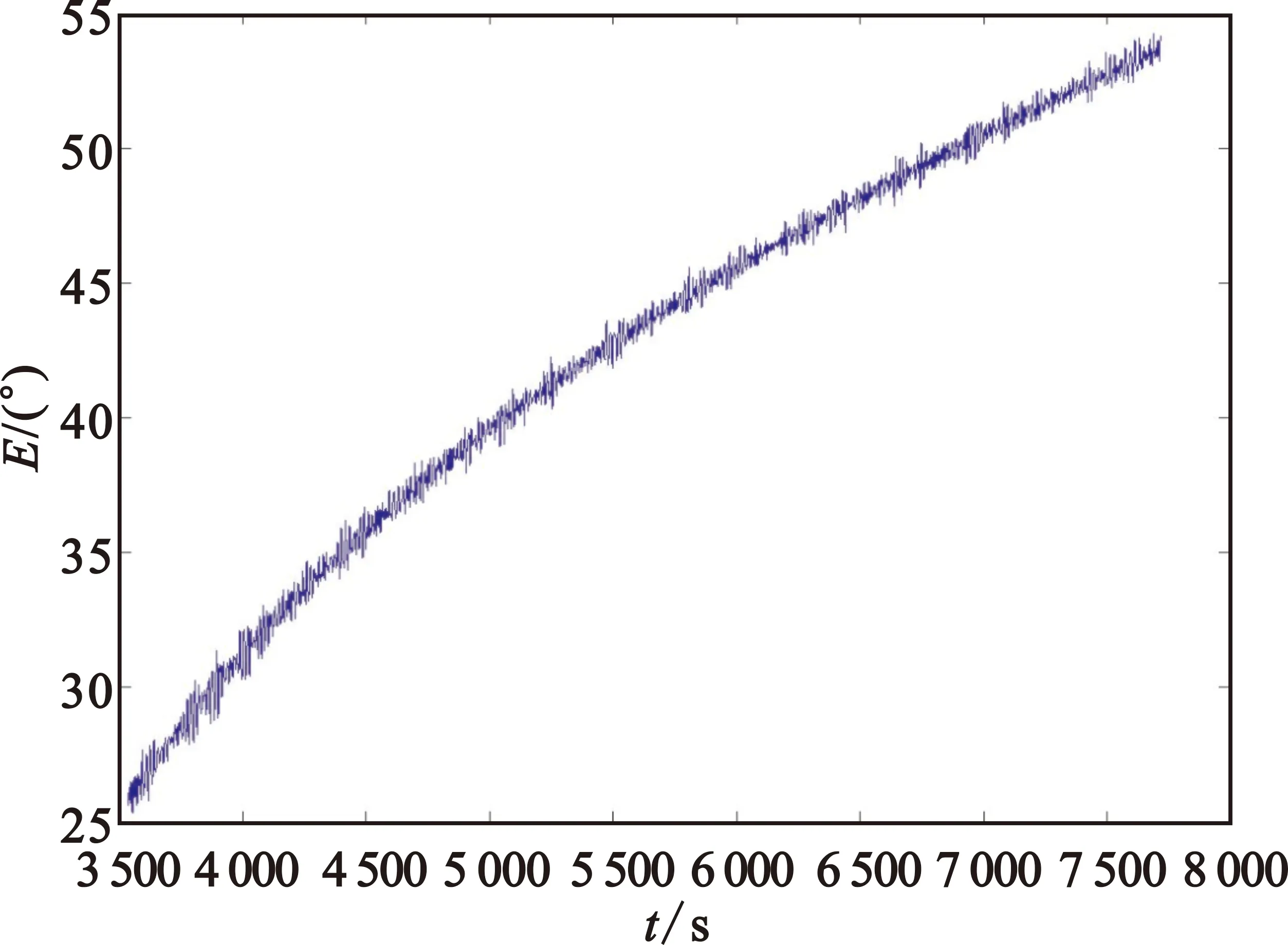
图13 检择后雷达2俯仰角Fig.13 Elevation angle measurement data from Radar 2 after detection

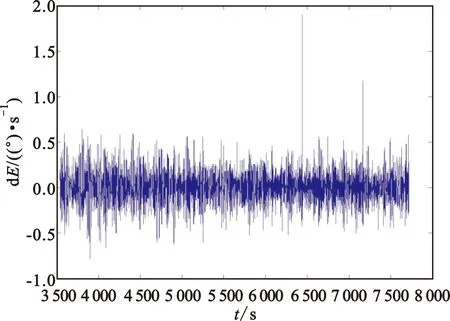
图14 检择后雷达2俯仰角差分图Fig.14 The first order difference of elevation angle measurement data from Radar 2 after detection

5 结论

外测设备数据检择对于提高后续的数据处理精度有着相当重要的意义，本文提出的利用两套设备的外测数据进行融合实现数据检择的方法能够显著提高剔野的精度，算法实时高效，并且可以从两套设备推广到多套设备。后续如果有3套或者更多设备参加，算法简单改进就可直接应用，而且参试的外测设备越多，融合的精度越高，检择的效果越好。

[1] 胡绍林，孙国基．靶场外测数据野值点的统计诊断技术[J]．宇航学报，1999，20(2)：68-74．

HU Shaolin,SUN Guoji. Statistical diagnosis method for outliers from spacecraft tracking data[J].Journal of Astronautics,1999,20(2):68-74.(in Chinese)

[2] 安振军，王敏，胡绍林，等．外弹道测量数据采集与处理技术[J]．飞行器测控学报，2005，24(2)：56-60．

AN Zhengjun,WANG Min,HU Shaolin,et al.Tracking data collection and processing technologies[J].Journal of Spacecraft TT&C Technology,2005,24(2):56-60.(in Chinese)

[3] 王正明，王宝智．异常观测数据的逐点剔除法[J]．数学的实践与认识，1997，27(3)：266-274．

WANG Zhengming,WANG Baozhi. One by one-method of outliers rejection in linear regression model[J].Mathematics in Practice and Theory,1997,27(3):266-274. (in Chinese)

[4] 祝转民，邱宏兴，李济生，等．动态测量数据野值的辨识与剔除[J]．系统工程与电子技术，2004，26(2)：147-190．

ZHU Zhuanming,QIU Hongxing,LI Jisheng,et al.Identification and elimination of outliers in dynamic measurement data[J].Systems Engineering and Electronics,2004,26(2):147-190. (in Chinese)

[5] 范顺西，胡绍林，楼琳，等．雷达数据斑点诊断与修复新方法[J]．宇航动力学学报,2011，1(2)：117-120．

FAN Shunxi,HU Shaolin,LOU Lin,et al.New approaches to diagnose and repair patchy outliers in radar data[J].Journal of Astrodynamics,2011,1(2):117-120. (in Chinese)

[6] 童丽，周海银．异常数据剔除的一种改进计算方法[J]．中国空间科学技术,2001，8(4)：11-15．

TONG Li,ZHOU Haiyin. An improved algorithm for the rejection of outliers data[J].Chinese Space Science and Technology,2001,8(4):11-15. (in Chinese)

[7] 卓宁．靶场外弹道数据处理中野值点剔除方法[J]．测试技术学报,2008，22(4)：313-317．

ZHUO Ning. Study on outliers eliminating method for data processing of exterior trajectory[J].Journal of Test and Measurement Technology,2008,22(4):313-317. (in Chinese)

[8] 祝转民，李济生，黄永宣．外弹道测量数据野值的递推辨识[J]．飞行器测控学报，2001，20(3)：55-60．

ZHU Zhuanming,LI Jisheng,HUANG Yongxuan. Identification and elimination of outliers in tracking data[J].Journal of Spacecraft TT&C Technology,2001,20(3):55-60. (in Chinese)

[9] 李辉芬，周锦标，何剑伟，等．航天测量船外测数据异常值自适应处理算法设计[J]．电讯技术，2011，51(4)：54-59．

LI Huifen,ZHOU Jinbiao,HE Jianwei,et al.Adaptive processing of abnormal value in measured data by space tracking ship[J].Telecommunication Engineering,2011,51(4):54-59. (in Chinese)

[10] 李辉芬，朱伟康，周朝猛，等．船载USB瞬时站址残差异常情况分析[J]．电讯技术,2010，50(2)：57-62．

LI Huifen,ZHU Weikang,ZHOU Chaomeng,et al.Exceptional phenomenon analysis of instrumentation ship’s USB residual error[J].Telecommunication Engineering,2010,50(2):57-62.(in Chinese)

[11] 凌林本，李滋刚，陈超英，等．多传感器数据融合时权的最优分配原则[J]．中国惯性技术学报,2000，8(2)：36-39．

LING Linben,LI Zigang,CHEN Chaoying,et al.Optimal weight distribution principle used in the fusion of multi sensor data[J].Journal of Chinese Inertial Technology,2000,8(2):36-39. (in Chinese)

[12] 王光新，王云江，吴翊,等．基于加权融合的多信源弹道数据实时野值检测方法[J]．飞行器测控学报,2005，24(6)：44-48．WANG Guangxin,WANG Yunjiang,WU Yi,et al.Real-time outliers detection in multi-source trajectory data based on weighted fusion[J].Journal of Spacecraft TT&C Technology,2005,24(6):44-48. (in Chinese)

[13] 吴金美，胡上成，凌晓冬．多项式拟合法在船载外测数据实时压缩算法中的应用[J]．电讯技术,2011，51(12)：68-72．

WU Jinmei,HU Shangcheng,LING Xiaodong. Application of polynomial fitting in real-time compressing algorithm for outer-trajectory measurement data of TT&C ship-borne equipment[J].Telecommunication Engineering,2011,51(12):68-72. (in Chinese)

Real-timeOutliersDetectionofShip-borneOuter-trajectoryMeasurementData

WU Jinmei,HOU Yawei,LI Yonggang,LING Xiaodong

(China Satellite Maritime Tracking and Control Department,Jiangyin 214431,China)

Characteristics of the missions for space TT&C ship and the outliers in the trajectory data are analyzed in order to study the method of real-time outliers detection. By cross-checking the trajectory data from two equipment,the influence of ship posture is removed. The models of adaptive weight and adaptive threshold value are built. The distributed real-time outliers detection method in ship-borne trajectory data is proposed based on coordinates transformation and weighted fusion. Computational results show that the algorithm can solve the detection problem in real time efficiently before the main data processing.

space TT&C ship;trajectory data;real-time outliers detection；weighted fusion

10.3969/j.issn.1001-893x.2017.12.019

吴金美，侯亚威，李永刚，等.船载外测数据的实时检择方法[J].电讯技术，2017,57(12):1457-1463.[WU Jinmei,HOU Yawei,LI Yonggang,et al.Real-time outliers detection of ship-borne outer-trajectory measurement data[J].Telecommunication Engineering,2017,57(12):1457-1463.]

2017-03-14；

2017-07-16

date:2017-03-14；Revised date：2017-07-16

wjm_83@aliyun.comCorrespondingauthorwjm_83@aliyun.com

TN957.52；V557

1001-893X(2017)12-1457-07