含风电的区域电网功率振荡特性分析与综合控制*

2017-12-20朱晓荣陈玉伟张祥宇王慧

电测与仪表 2017年1期

朱晓荣，陈玉伟，张祥宇，王慧

（华北电力大学新能源电力系统国家重点实验室，河北保定 071003）

0 引言

随着风电装机比例逐渐升高，变速风机不同于传统发电机的控制方式给电网安全稳定运行带来了新的挑战。由于变速风机几乎失去了频率响应，大规模并网必然会导致系统频率调整能力不足［1-4］。目前，将比例-微分（proportional derivative PD）控制附加在最大功率跟踪之上，已成为解决风电调频问题普遍采用的控制方案［5-7］。然而，电网惯量大小通常与系统的振荡模式和衰减特性密切相关。上述频率控制器的设计并未考虑有功调节对系统阻尼特性的影响，若调频时注入系统的有功功率引起系统低频振荡，将会降低系统动态稳定，从而影响控制器的推广应用。因此研究风电频率控制对电网低频振荡的影响具有重要的理论和实际意义。

变速风电机组的附加频率控制器通过调节风机输出功率实现调频功能，利用微分环节虚拟机组的惯性响应，利用比例环节模拟机组的一次调频动态过程。在系统频率变化时，风电机组快速调节电磁功率，必然会引起区域电网阻尼特性的变化［8-11］，其中，文献［9-10］通过理论分析，证明了惯性控制的微分项系数容易引入负阻尼。为协调解决频率控制与阻尼控制间的矛盾，文献［12-13］将频率控制与区域间振荡补偿器相结合，获得了良好的控制效果，但控制难度较大，参数计算复杂。文献［14-15］虽有效地阻尼了区域间功率振荡，但却使风电机组失去了惯性响应，没能充分发挥风机的调频能力。目前，风电的频率与阻尼控制问题尚未得到有效解决。风电处在不同并网位置时，电网结构与风电频率控制对系统区域间低频振荡的影响，需进一步深入探讨，进而优化设计频率控制器，协调解决上述两种控制功能，使风电能够具备更完善的功率支持能力。

文中在深入研究变速风电机组改善系统阻尼特性原理的基础上，针对附加频率控制器中微分项引入负阻尼的不利影响，提出通过增加一阶惯性环节，使频率控制对电网低频振荡始终表现为正阻尼特性的改进控制策略。为验证所提控制策略的有效性，本文在DIgSILENT/PowerFactory仿真软件中建立包含一双馈风电场的仿真模型，针对风电渗透率约为30%的区域互联系统进行模态和时域仿真验证。

1 频率控制器对功率振荡的影响

基于PD控制器的风电机组附加频率控制技术初步解决了风电与电网电气解耦而造成的削弱系统频率稳定的问题。然而，变速风电机组的附加频率控制在有功调节过程中对系统阻尼特性同样存在影响。下面分析风电机组的PD控制器对系统阻尼影响的原理。

图1为含风电场的区域电网的等值电路图。其中，UG为风电场并网点电压；E′为G1的q轴暂态电势；U为无限大电源G2端电压；θ为E′和UG之间的相角差；δ为E′和U之间的相角差；x1与x2分别为线路电抗参数；B3为系统的平衡节点。

图1 风电场并网等值电路图Fig.1 Equivalent circuit of power system in a wind farm

如图1所示，线路B1-B2和线路B2-B3输送的有功功率分别为：

由系统功率平衡关系可得：

假定同步发电机G1原动机输出功率不变，采用q轴暂态电势E′恒定的二阶经典发电机模型，则G1的线性化转子运动方程可表示为：

式中TG和DG分别为同步发电机G1的惯性时间常数和阻尼系数。

为简化分析，假定线路母线电压恒定，因此线路上功率的变化仅取决于母线电压相角的变化。分别对式（1）、式（2）求小扰动量。

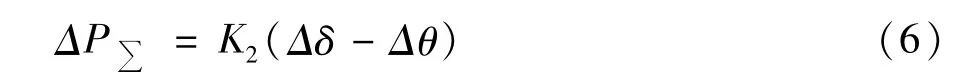
系统发生小扰动时，在比例微分控制下，双馈风机输出有功的变化量为：

将式（5）～式（7）代入（3）解得：

式中K=K1/（K1+K2）。

将式（8）代入式（4）得到PD控制器下发电机G1的小扰动转子运动方程。

由式（9）可以看出，双馈风机在PD控制下向系统注入有功功率时，改变了系统中同步发电机的功角变化，比例项系数等效增大同步发电机的阻尼系数，给发电机的功角振荡引入正阻尼；而微分项系数则等效增大同步发电机的惯性时间常数，但却给同步发电机的功角振荡引入了负阻尼。

2 变速风电机组的频率改进控制方法

风电机组的微分控制环节引入负阻尼的问题，使其在调频过程中具有诱发低频振荡的风险，从而影响控制技术的实际应用。为解决上述问题，风电机组的附加频率控制器需要进一步完善，使改进控制器兼有频率调节和增加阻尼两种控制功能。

图2所示为变速风电机组的改进频率控制器的结构图。其中，虚拟惯性控制被进一步改进为带有一阶惯性滞后的微分控制环节，在此基础上，通过合理配置该控制器的参数，可使双馈风力发电机组的频率控制始终表现为正阻尼特性。

图2 频率控制的改进方案Fig.2 Improved scheme of frequency control

认为正弦振荡的转子角Δδ=δmsin（ωosct），则频率变化量可表示为：

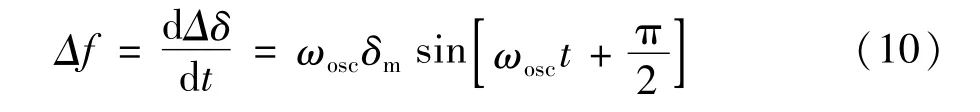
由式（10）可知，Δf与Δδ的相位差为π/2，即Δf=jωoscΔδ=sΔδ。

如图2所示，在一阶惯性-微分控制环节作用下，双馈风机输出有功的变化量可表示为：

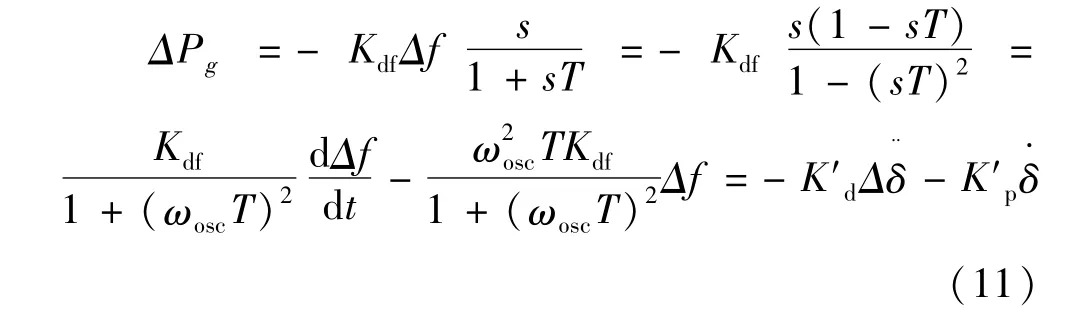
将式（5）、式（6）、式（11）代入式（3）解得：

将式（12）代入式（4）得到发电机G1的小扰动转子运动方程为：

由式（13）可知，所提改进频率控制器通过微分与一阶惯性环节共同模拟风电机组的惯性响应，控制环节中的微分环节在等效增加同步发电机惯性时间常数的同时，也使得同步发电机阻尼系数增加为DG+KK′p。因此，改进后的频率控制可以在实现风电机组频率控制过程中，同时增强区域电网阻尼的控制目标。其中，所提频率改进控制方案中一阶惯性环节的控制参数T取值范围可由下面方法求得。

求式（13）所示微分方程的特征根，得其实部λ为：

改进频率控制器若要增加系统阻尼，则λ应随Kdf的增加而减小，即dλ/dKdf＜0。此外还应保证λ随T的增加而减小，即dλ/dT＜0。综上，解得惯性环节时间常数T的取值范围为：

3 含风电的两区系统的振荡模态分析

3.1 系统简介

为验证本文提出的改进控制策略的有效性，利用DIgSILENT/PowerFactory仿真软件建立如图3所示的仿真系统，该系统包含一个容量为500×2 WM的双馈风电场，和两个容量分别为900 MVA的火电厂G1和1 800 MVA的火电厂G2。负荷L1、L2容量分别为800 MW、1 700 MW。母线B2为仿真系统的平衡节点，风电场和火电厂均视为等值机组。仿真结果中功率、转速和电压均采用标幺值，选取各个发电厂的额定容量为其功率基值。

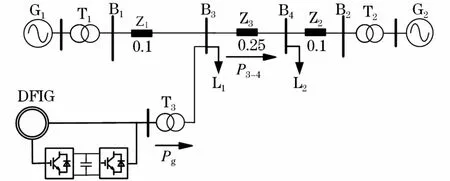
图3 含风电场的系统仿真模型结构Fig.3 Network of simulation model for wind power system

3.2 PD控制器对低频振荡的影响

在图3所示系统仿真模型中，将PD控制器中比例项系数Kpf从0增加到50，得到系数Kpf对系统区域间低频振荡模态影响的变化轨迹如图4（a）所示；然后再将微分系数Kdf从0增加到30，得到系数Kdf对系统区域间低频振荡模态影响的变化轨迹如图4（b）所示。

图4 PD控制器对低频振荡模态的影响趋势Fig.4 Effects trends of PD control on low frequency oscillation modes

由图4（a）可以看到，随着风机附加频率控制比例项系数Kpf的增大，系统区域间低频振荡模态的特征值逐渐远离复平面的虚轴，表明区域间的振荡阻尼在增大，即系数Kpf为发电机低频振荡引入正阻尼。而由图4（b）可以看到，随着风机附加频率控制微分项系数Kpf的增大，系统区域间低频振荡模态的特征值逐渐靠近复平面的虚轴，表明区域间的振荡阻尼在减小，即系数Kpf为发电机低频振荡引入负阻尼。因此，在区域间振荡阻尼较小的互联电网中，PD控制器有诱发区域间功率振荡的可能，从而使得传统PD控制器在实际应用中存在启动难题。

3.3 改进频率控制对低频振荡的影响

在图3所示系统仿真模型中，将改进频率控制器中比例项系数Kpf从0增加到50，得到系数Kpf对系统区域间低频振荡模态影响的变化轨迹如图5（a）所示；然后设置一阶惯性时间常数T=0.6，并将微分系数Kpf从0增加到30，得到系数Kpf对系统区域间低频振荡模态影响的变化轨迹如图5（b）所示。

图5 改进控制对低频振荡模态的影响趋势Fig.5 Effects trends of improved control on low frequency oscillation modes

根据图5（a）、图5（b）可知，当采用带有一阶惯性的微分时，随着比例项系数Kpf和微分项系数Kdf的增大，系统区域间低频振荡模态的特征值都逐渐远离复平面的虚轴，表明区域间的振荡阻尼在增大。由此说明改进频率控制器能够对系统低频振荡始终表现为正阻尼特性，消除了PD控制器可能诱发低频振荡的的不足。

4 仿真分析

为进一步验证风电机组在所提控制策略下的调频能力以及对区域电网间功率振荡的阻尼作用，在图3所示的仿真系统中，通过设置以下三个仿真案例进行对比分析。

（1）无附加控制，即Kpf=0，Kpf=0，T=0；

（2）传统 PD控制器，即Kpf=10，Kpf=30，T=0；

（3）改进频率控制，即Kpf=10，Kpf=30，T=0.6。

负荷L1在t=2 s时，突增300 MW，风电机组在上述三种控制策略下，分别得到风电机组电磁功率、系统频率、联络线B3-B4输送功率P3-4、以及发电机G1与G2相对转子角δ1-2的动态响应曲线，如图6～图9所示。

图6 DFIG电磁功率动态响应曲线Fig.6 Dynamic response curves of DFIG’s electromagnetic power

图7 系统频率动态响应曲线Fig.7 Dynamic response curves of the system frequency

从图6、图7可以看出，风电机组在无附加控制时，系统负荷增加后，风机输出功率几乎没有变化，从而造成系统频率大幅跌落。采用传统PD控制后，风电机组对于频率降低具有一定的支持作用，但引起了风电场输出功率的振荡，不利于风机的安全稳定运行。而风电机组在采用所提改进频率控制策略后，风电场输出电磁功率曲线变化更加平滑，与相对传统PD控制相比，改进频率控制策略的调频效果更好。

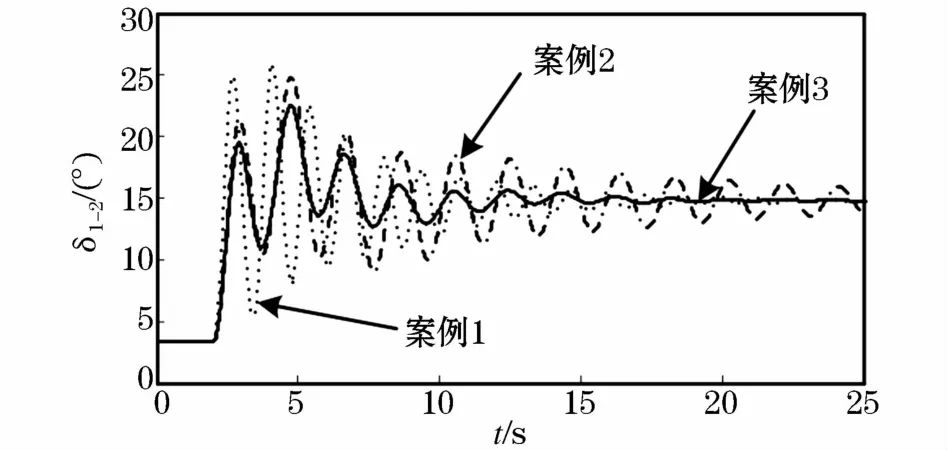
图8 转子角δ1-2动态响应曲线Fig.8 Dynamic response curves of rotor angleδ1-2

图9 联络线输送功率P3-4动态响应曲线Fig.9 Dynamic response curves of power P3-4

从图8、图9可以看到，采用传统PD控制后，由于微分项系数系数Kdf引入负阻尼，使得发电机G1与G2相对转子角δ1-2以及联络线B3-B4输送功率P3-4响应曲线出现振荡。而采用所提改进频率控制策略后，相对转子角δ1-2和功率P3-4响应曲线衰减速度明显加快，在负荷突变10 s后已经趋于稳定，从而说明改进控制策略为系统引入正阻尼。以上时域仿真证明了所提改进频率控制策略能够兼有系统频率调整和阻尼区域功率振荡的综合能力。