编程软件在齿轮测绘中的应用

刘亮亮*，郭勇，杜博群，孙玲玲

（山推工程机械股份有限公司 传动分公司，山东济宁，272073）

编程软件在齿轮测绘中的应用

刘亮亮*，郭勇，杜博群，孙玲玲

（山推工程机械股份有限公司 传动分公司，山东济宁，272073）

机械设备维修过程中，常涉及齿轮类零件的再制造问题。而再制齿轮能否顺利匹配使用，齿轮的测绘精度就显得尤为重要。通常的测绘方法，先通过齿轮的几何尺寸进行初步计算，再利用现行标准进行参数选取及计算。这种方法精度较低，特别是对于斜齿轮，误差更大。本文在阐述齿轮的测量原理的同时，引入编程算法。利用编程软件中的循环命令，对齿轮参数进行大量的匹配计算，从中找到最接近原始齿轮的参数，从而提高测量精度及速度。

齿轮测绘；编程软件；循环命令；计算原理

引言

当前，随着设计理念的不断创新、制造技术的飞速发展，产品更新换代间隔逐年缩短，即便是发展相对缓慢的工程机械制造领域，产品也更新了几代。虽然新产品无论是外观、功能或是品质都有相当大的提升，但出于经济原因，市场上还大量充斥着旧型号产品，因为年代久远，部分产品早已经停产，相关配件也已买不到，所以这些产品一旦出现故障，要么报废，要么自己加工零件匹配，而要自己加工，首先要有零件的尺寸参数，这就需要对原零件进行测绘。齿轮，是工程机械传动系统中不可或缺的关键零件，同时也是较难精准测量的零件之一。齿轮测绘难点主要在参数的确定，参数的精确与否，直径影响配做齿轮能否正常运转。 本文中，通过编程软件在齿轮测绘计算中的应用示范，提出一种较合理、精确的齿轮参数确定方法。

1 齿轮参数确定方法

1.1 能够测得

① 齿数，齿轮测绘中最直观的参数，直接查得。

② 齿顶圆直径，对于偶数齿，可直接用卡尺测量，对于基数齿，需要用到三角函数换件，间接求得（关于齿顶圆的测量，相关文章较多，本文不在详细叙述）。

③ 齿根圆测量，与齿顶圆的测量方法基本一样。

④ 跨k齿公法线值，使用公法线千分尺测量。

⑤ 其他结构尺寸。

1.2 需要计算确定的参数

要加工齿轮，除结构尺寸外，需要确定的齿部参数包括：

①模数，模数是决定齿轮大小的重要因素，是齿轮的基本参数。

②法向齿形角，决定齿廓形状，受力角度。

③变位系数，影响齿轮大径及齿厚。

④螺旋角，斜齿轮关键参数，螺旋角不匹配就无法啮合。

1.3 齿轮参数确定方法

为方便叙述，我们将齿轮各参数用下列代号表示：

已知参数（测绘得到的参数）：

z—齿数；W（k）—跨 k齿公法线；k—跨齿数；da—齿顶圆直径；df—齿根圆直径

希望计算求得的参数：

m—模数；αn—法向齿形角 ；β—螺旋角；x—变位系数；

叙述过程需要用到的参数：

ha—齿顶高 △y—齿顶高变动系数 ha*—齿顶高系数d—分度圆直径 αt—端面齿形角

①模数（m）的确定方法

常规方法：

对于外齿直齿轮，因为 齿顶圆直径（da）与模数（m）间存在以下关系：

da=d+2ha=mz+2(ha*+x-△y)m （机械设计手册第3卷）

式中， ha*通常取值为1，在齿轮变位系数很小的情况下，x-△y值也比较小，上式可近似为：da=d+2ha=mz+2m 可得m=da/(z+2) 按照标准模数进行取整，可求得m值。

但是，对于变位系数较大的齿轮，x-△y值较大不能忽略不计的情况下，上述近似关系就难以成立了，在采用上述方法计算m值，误差也将很大。而且，上述方法仅适用于圆柱直齿轮，对于斜齿轮需要预先知道螺旋角β值。

利用软件编程计算：

通过对齿轮跨齿数公法线的计算方法的分析，我们可以发现，不同跨测齿数公法线之差与模数存在一定的比例关系：以跨k齿和k+1齿为例

跨 k+1 齿公法线 W（k+1）=cosαn(π（k+1-0.5）+z’invα)m+2 m xsinαn

跨 k 齿公法线 W（k）=cosαn(π（k-0.5）+z’invα)m+2 m xsinαn

则 W（k+1）- W(k) = mπcosαn 其中 W（k+1）与 W(k)为可测值，m与αn都是我们要求的值，此时通过编程软件的循环命令语句，就可将满足上述公式，同时符合相关标准（标准模数、标准压力角）的m值及αn 值得出。该方法较较前一种方法更可靠精确，同时可直接求得αn值，而且此方法同样适用于斜齿轮法向模数计算。

②法向压力角αn的计算方法

常规方法，在计算取得m后，可通过关系式W（k+1）- W(k)= mπcosαn 求得，但前提是保证m数的准确性。

如果利用软件编程计算，αn可与m值一起得出。

③变位系数x值计算

常规方法1：根据关系式da= mz+2(ha*+x-△y)m，其中△y一般都非常小，则上式

可近似为：da =mz+2(ha*+x)m 得到 x=(da-mz)/m /2

但是，很多情况下，出于避免干涉的需要，齿轮的齿顶圆直径人为的进行了缩小，

此种情况下，测量的齿顶圆直径本身就低于理论值，同样，用此值进行计算的x值误差也会很大。

常规方法2：利用公法线计算公式W (k)=m{cosαn[π（k-0.5）+z invαn]+2 x sinαn}

可得出 x={W(k)/m- cosαn[π（k-0.5）+z invαn]}/2/sinαn ；

上述两种方法仅适用于圆柱直齿轮，或者在已知螺旋角的情况下，用于斜齿轮计算。

利用软件编程计算：根据公式 W (k)=m{cosαn[π（k-0.5）+z’invαn]+2 x sinαn}

其中 z’=z.invαt/invαn tanαt=tanαn/cosβ

利用VB编程软件的循环命令，同时设定好x和β的取值范围（、W(k)的偏差范围，就可得出符合上述公式条件的x值及β值。

④螺旋角β计算

常规方法：角度仪测量。

与测量者的水平有很大关系，对于18.5 °、20.5°等带有半度的角度很难判定，

总体误差较大。

利用软件编程计算：可与x值同时得出，准确度更高。

2 示例说明

2.1 数据测量（图1）

齿轮z，实测公法线W（k）、W（k+1），跨测齿数k

2.2 计算模数（m）及法向齿形角(αn)

2.2.1 程度中的设定

① 设定公法线差值 Wx=W（k+1）- W(k) = mπcosαn；

② 设定公法线测量误差，理论上设定越小计算越准确，但考虑到可能出现的误差情况，初始设定0.05，如果最终得出值过多，可适当减小。

③ 根据国标模数（图3）标准，设定m值循环起始值为0.25，循环间隔0.25

④ 根据常用压力角的取值特征，设定 αn起始值 12.5，循环间隔2.5

2.2.2 利用循环命令计算

最终结果，如图3，如果最终结果出现多项，选取符合相关标准（GB、ISO）选项，极个别情况可能出现所测绘齿轮为特殊非标齿轮的情况，建议贴近现有标准重新设计，否则很难找到加工方或投入巨大。

图1 数据测量

优选标准模数及压力角

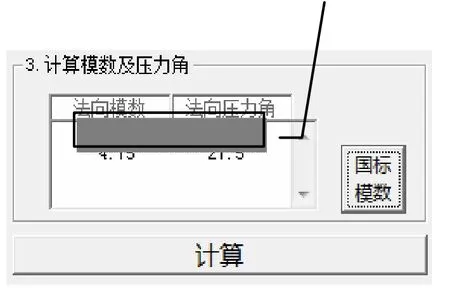
图2 计算模数及压力角

图3 国标模数

2.3 计算变位系数

2.3.1 赋值（图4）

图4 参数赋值

① 引入3.2中计算出的模数及压力角

② 选择齿形

2.3.2 程序内的设定

① 设定公法线偏差范围，根据统计，实际公法线与基础公法线偏差（外齿）在-0.05到-0.25左右，但是如果测量齿轮齿面磨损明显，应适当将上下偏差值降低。

② 设定螺旋角范围，一般在8-25之间。

③ 设定变位系数范围 ，一般在-1到+1之间。

④ 理论公法线基础值：

W（k）’=m{cosαn[π（k-0.5）+z’ invαn]+2 .x. sinαn}

其中 z’=z. invαt/invαn tanαt=tanαn/cosβ

2.3.3 利用循环命令计算

For β =8 To 25 Step 0.5

For x = -1 To 1 Step 0.01

If W（k） - W（k）’ ＜= -0.05 And W（k） - W（k）’ ＞=-0.25 Then

Text7.Text = β ，x

(—如果实测公法线与理论公法线差值在公法线偏差范围内，在文本7中显示β、x值)

End if

Next x

Next β

2.3.4 结果输出

如图5，一般，x 值会出现多个，但都比较相近，

选择任何一个都是可以的。

图5 结果输出

至此，被测齿轮的模数（m）、变位系数（x）、齿形角αn，螺旋角 β都已经得出，加上已知的齿数（z）及自定的精度等级等 ，齿轮加工所需参数就齐备了。

3 特别说明

（1）对于齿轮的测绘，为进一步提高准确性，最好对一个齿轮副的两个齿轮同时进行测绘计算，它们的模数、齿形角、螺旋角（角度一样，方向相反） 相同，变位系数之间存在关联，可更好的额进行比对和选择。

（2）最后结果输出时，可能出现无结果情况，请再次确认测量数据的准确性（特别是公法线），如果测量数据无误，可适当调整设定值的取值范围再次计算。

（3）在3.2.2及3.3.3中的程序仅是为了方便叙述而做的示范性语句，实际程序内还应包括参数赋值、单位换算、关联公式等一系列内容。

4 结束语

利用编程软件的循环命令特性，可完成对齿轮参数数以万计及以上的匹对工作，能够更精准、更快速的完成齿轮参数的选定，这是传统人工方法所不能比拟的。通过实例验证，该方法较传统方法精度更高，且避免了人为误差的可能性，同时对于传统方法较难测绘的斜齿轮，同样适用。

[1]秦永德. 机器测绘[M]. 北京： 北京理工大学出版社,2012.

[2]林卓然. VB语言程序设计[M]. 北京： 电子工业出版社,2009.

[3]成大先. 机械设计手册. 北京： 化学工业出版社,2002.

[4]张展,实用齿轮设计计算手册. 北京： 机械工业出版社,2011.

[5]田培棠. 圆柱齿轮几何计算原理及使用算法[M]. 北京： 国防工业大学出版社,2012.

[6]张枫念,工程数据算法和VB编程实例[M]. 北京： 化学工业出版社,2017.

[7]夏齐霄. 机械设计 VB编程基础及应用实例[M]. 北京： 国防工业出版社,2010.

Application of Programming Software in Gear Mapping

LIU Liangliang*,GUO Yong,DU Boqun,SUN Lingling
（Transmission Components Division,Shantui Construction Machinery Co.,Ltd.,Shandong Jining,272073,China）

The remanufacturing of gear parts is often involved in the maintenance of mechanical equipment.And then the gear can be successfully used for matching,gear mapping accuracy is particularly important. Usually the method is first calculated by the geometric dimension of the gear,and then the parameters are selected and calculated by using the current standard,The accuracy of this method is low,especially for helical gears. In this paper,the principle of measurement is introduced,and the programming algorithm is introduced. By using the cyclic command,a large number of matching calculation of gear parameters is carried out,and the closest parameters are found,so as to improve the measurement accuracy and speed.

gear mapping; programming software; Circular command; Calculation principle

TG86

A

1672-9129(2017)06-0030-03

10.19551/j.cnki.issn1672-9129.2017.06.010

刘亮亮,郭勇,杜博群,等. 编程软件在齿轮测绘中的应用[J]. 数码设计,2017,6(6)： 30-32.

Cite：LIU Liangliang,GUO Yong,DU Boqun,et al. Application of Programming Software in Gear Mapping[J]. Peak Data Science,2017,6(6)：30-32.

2017-02-06；

2017-03-12。

刘亮亮（1982.10-），男，.山东济宁 ；职务：技术主管；学历：大学本科；工作单位：山推工程机械股份有限公司。

Email：meiyoulxy@163.com