区间值模糊信息系统的粗糙隶属度

张佳，张晓燕*，徐伟华

（重庆理工大学理学院，重庆，400054）

区间值模糊信息系统的粗糙隶属度

张佳，张晓燕*，徐伟华

（重庆理工大学理学院，重庆，400054）

Pawlak.Z的粗糙集理论与区间值模糊集相结合可以得到区间值模糊信息系统。本文在已有的区间值模糊信息系统概念的基础上，根据模糊等价关系引入了模糊近似空间。从而给出了相似度，进而利用模糊近似空间中任意两个对象集的相似度，定义了区间值模糊信息系统的粗糙隶属度并讨论研究了粗糙隶属度的相关性质。最后，实例验证了这些性质的可行性和有效性。

粗糙集；区间值模糊信息系统；模糊等价关系；粗糙隶属度

引言

1965年，美国著名控制论专家Zadeh教授提出了模糊集理论[1]。模糊数学突破了经典数学的局限性，用于解决不确定性现象，使得数学的应用范围更加广阔。其中，模糊聚类，决策分析，模糊综合评判[2]，模式识别等被广泛地应用在医学，农业，科学，经济等各个领域。但是，Zadeh的模糊集理论仍有一定的局限性。因此，Dubois D 和Prade H[3]在Zadeh的基础上推广了模糊集理论，提出了区间值模糊集。在处理模糊信息时有效的保护了信息的完整性。目前，已经有许多学者进行了深入研究，并取得了一定的成果[4-5]。

粗糙集理论[6]最早在 1982年由波兰科学家Palwak创立，是一种刻划不完整性和不确定性的数学工具，能有效地分析和处理不精确、不一致、不完整等各种不完备信息。粗糙集理论是经典集合论的推广延伸，近些年将经典Palwak的粗糙集推广为多种形式[7-10]，使得粗糙集理论在多领域得到了迅速发展，研究逐渐趋热。特别地，粗糙集理论的应用[11-12]还包括了地震预报、数据挖掘[13]、模式识别、故障检测[14]、医疗诊断[15]、智能信息处理等领域。

粗糙隶属函数[16]的概念最初是Pawlak提出的，定义在对象集的等价类上，函数值不是和，而是区间。本文的第二部分介绍了基本的相关概念，对一些初步概念性质做了简单回顾。在第三部分中，定义了区间值模糊信息系统中的模糊等价关系，并建立了模糊近似空间。根据模糊等价关系又定义了区间值模糊信息系统的粗糙隶属度。由此，还提出了粗糙隶属度的一些重要性质并给予了证明。在最后，给出了一个例子来证明以上性质。

1 基本知识

区间值模糊信息系统是以区间作为属性值的信息系统，且区间在 [0,1]之间。

定义1.1[17]设论域U上的集合A是一个映射：

对于任意x∈U，则称A为一个模糊集合，A(x)为x对于A的隶属度。

定义 1.2 设U是一个非空有限论域，映射A：U→I[0,1]称为 U上的区间值模糊集。因此，对任意的其中 AL，AR都是U上的模糊集，分别代表A(x)的左，右两个端点值。 在区间值模糊集上定义运算：对于任意的x∈U，有

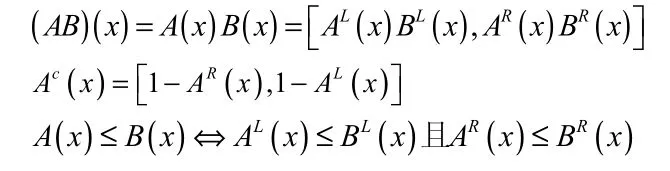
定义 1.3 区间值模糊信息系统为一个四元组I=(U,AT,V,f)三元组I=(U,AT,f)为信息系统其中

U={x1,x2,…,xn}是非空有限论域；

AT={a1,a2,…,am}是非空有限属性集；

f：U×AT→V 是一个信息函数使对任意的uk∈U在属性ai∈AT上对应一个区间值即对任意的 xk∈U ai∈AT有其中为[0,1]上的实数并且满足

定义1.4 设R是U上的一个模糊关系有

（1）R是自反的如果R(x,x)=1∀x∈U

（2）R是对称的如果满足∀x,y∈U有

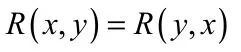
（3）R是传递的 如果满足∀x,y,z∈U有

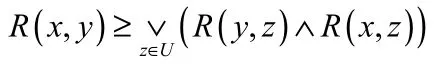
则R为 U上的一个模糊等价关系二元组(U,R)称为模糊近似空间。

定义1.5[18]设(U,R)为模糊近似空间 U是非空有限论域R为 U上的模糊等价关系S⊆U

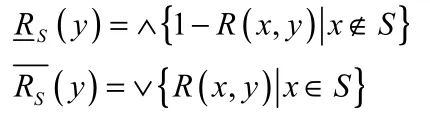
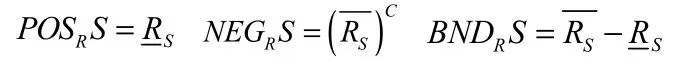
定理1.1 设(U,R)是模糊近似空间S,S1,S2⊆U 则

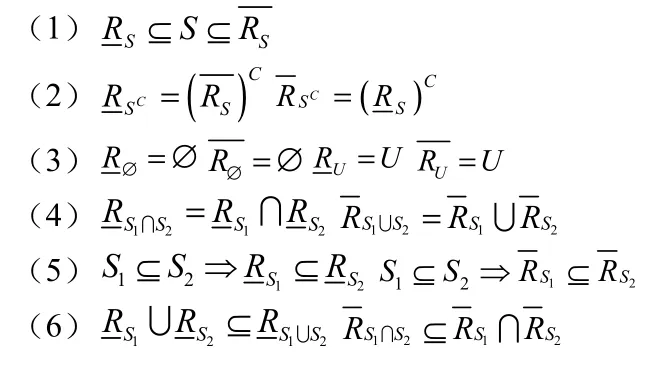
2 区间值模糊信息系统的粗糙隶属度

定义 2.1 设I=(U,AT,V,f)是一个区间值模糊信息系统∀at∈ATxi,xj∈U

其中RAT是相似关系根据定义1.4我们就可以将区间值模糊信息系统转化为在模糊近似空间(U,R)中。则下面两点成立：

（1）U是一个非空论域U到U的一个模糊二元关系RAT是U×U上的一个模糊集R：U ×U→[0,1]所以RAT为U上的模糊关系。

（2）显然RAT满足自反性对称性传递性所以RAT是一个模糊等价关系。

定义2.2 设I=(U,AT,V,f)是一个区间值模糊信息系统R是I上的模糊等价关系S⊆U ∀y∈U则y关于R在集合S中的粗糙隶属度为

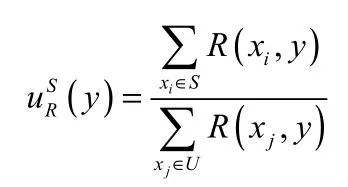
定理 2.1 设I=(U,AT,V,f)是一个区间值模糊信息系统R是I上的模糊等价关系S⊆U ∀y∈U其粗糙隶属度有以下性质：

证明：

（1）根据定义1.2当S=U时可以得到

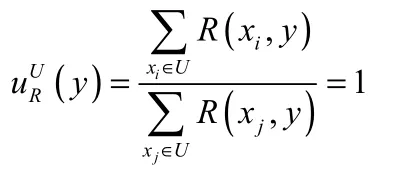
（2）根据定义 1.2和定理 1.1的（1）当S=∅对∀xi∈∅ R(xi,y)=0因此可得到

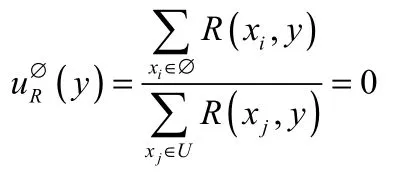
（3）根据定义1.5和定义2.2可得

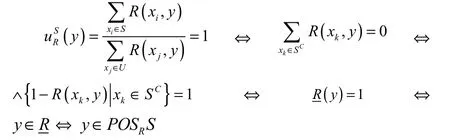
（4）根据定义1.5定义2.2和性质2.1的（2）可得

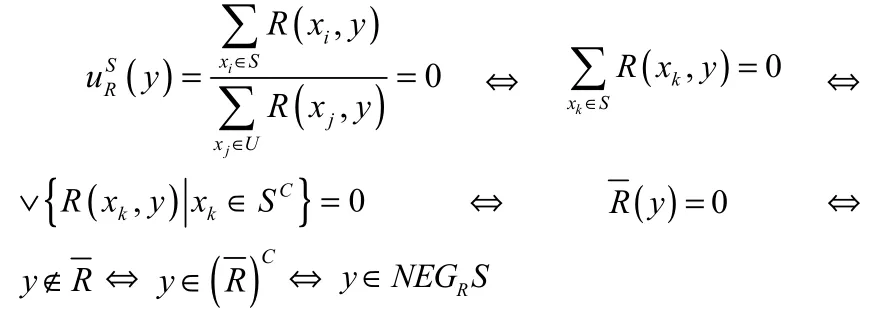
（5）由（3）和（4）可知结论成立

（6）根据定义2.2我们可以得到

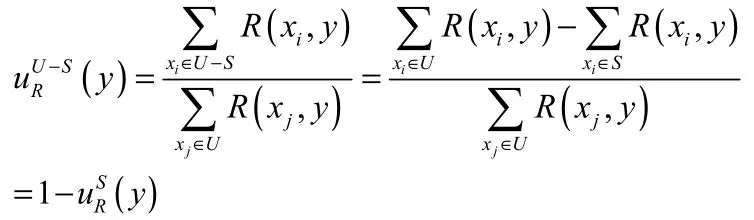
定理 2.2 设I=(U,AT,V,f)是一个区间值模糊信息系统R是I上的模糊等价关系S⊆U ∀y∈U则

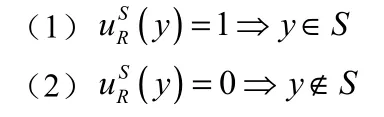
证明：

（1）根据定理2.1（3）有

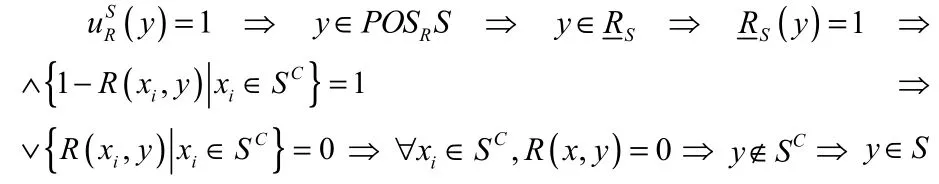
（2）根据定理2.1（4）有

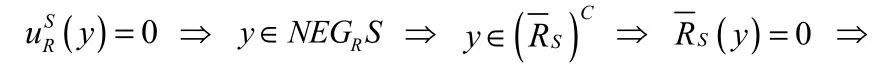
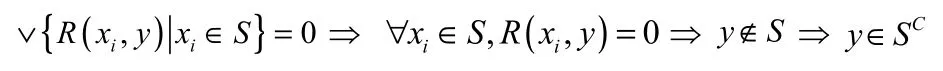
注：

定理 2.3 设I=(U,AT,V,f)是一个区间值模糊信息系统R是I上的模糊等价关系∀S1,S2⊆U∀y∈U则有

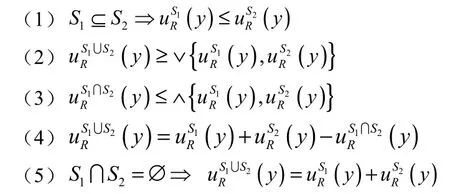
证明：

（1）当S1⊆S2时有

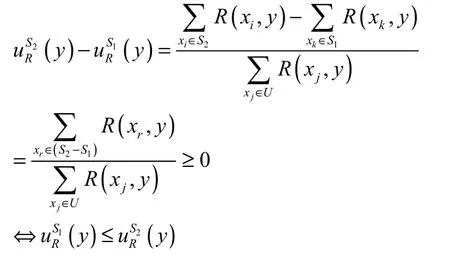
（2）因为

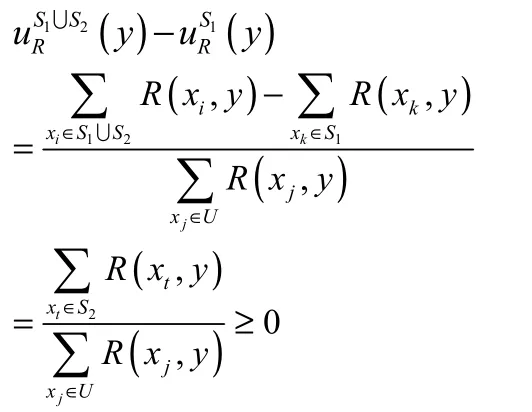
脱了衣服，竹韵才发觉刚才的热水已经给龙斌洗澡用完了，于是，她干脆扭开自来水龙头用凉水冲起来。水虽然有点凉，但还能适应，她边洗边想，下个月领了工资，首先得买台热水器，免得天天要烧水。

（3）因为

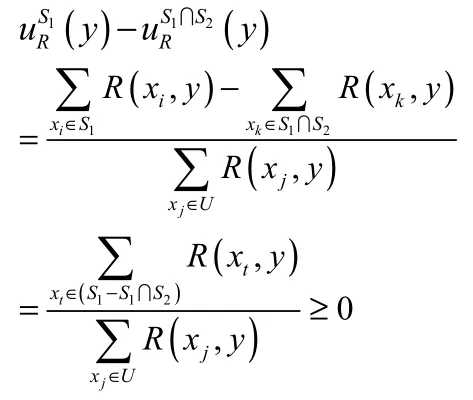
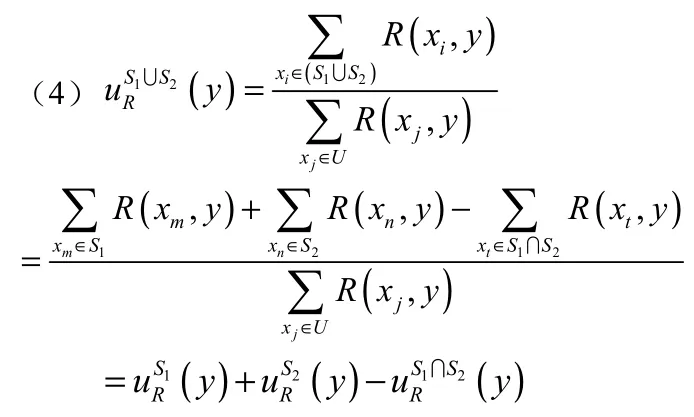
（5）由（4）得到

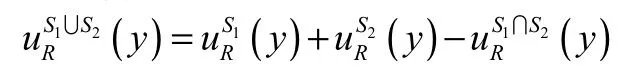
再根据定理2.1（2）知

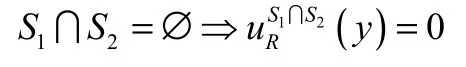
因此

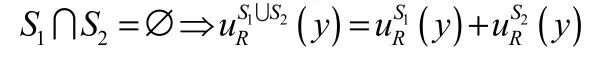
定理 2.4 设I=(U,AT,V,f)是一个区间值模糊信息系统R是I上的模糊等价关系S⊆U ∀y∈U S={S1,S2,…,ST}是一个集族其中∀Si,Sj∈S Si∩Sj=∅ 则有

（2）如果S={S1,S2,…,ST}是U上的一个划分则

证明：

（1）由定理2.3的（4）和（5）可得

因为S={S1,S2,…,ST}是U上的一个划分则∪Si=U（i=1,2,…,T）

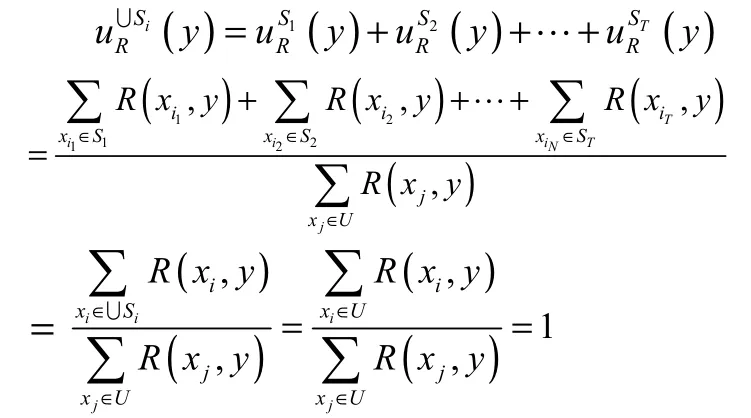
例2.1 如表1设I=(U,AT,V,f)是一个区间值模糊信息系统其中AT={a1,a2,a3,a4,a5}U={x1,x2,…,x10}R是I上 的模糊等价关系(U,R)是I上的模糊近似空间。

设S={S1,S2}为U的一个划分其中 S1={x1,x3,x6,x7,x10}S2={x2,x4,x5,x8,x9}

根据定义2.2我们可以得到xi关于R在S1,S2中的粗糙隶属度：

显然当{S1,S2}为U 的一个划分时上面的例子就可以说明对于任意的因此定理2.4成立。

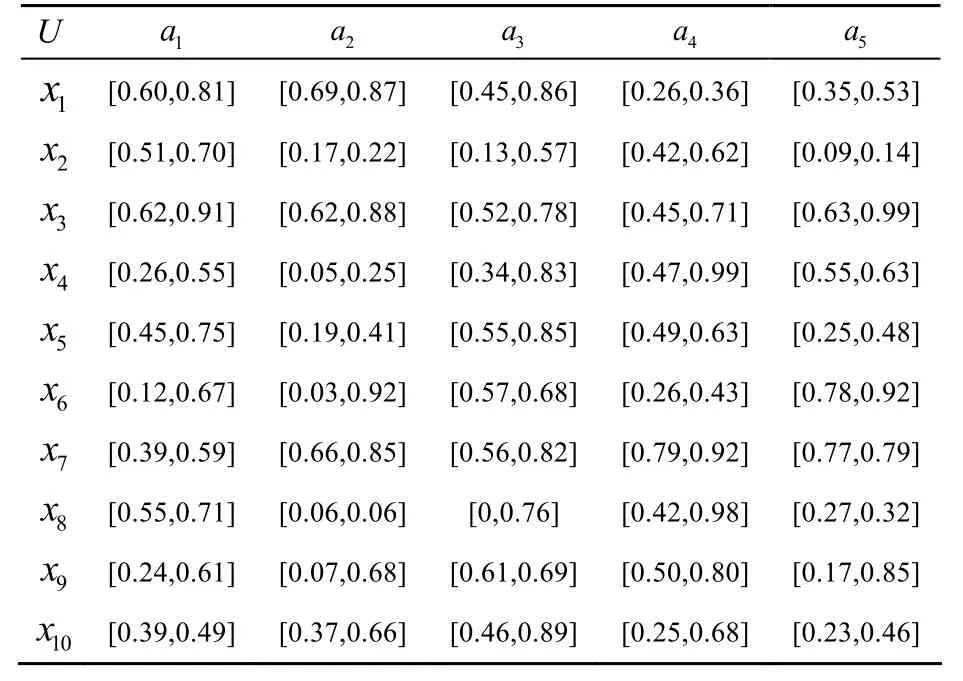
表1 区间值模糊信息系统

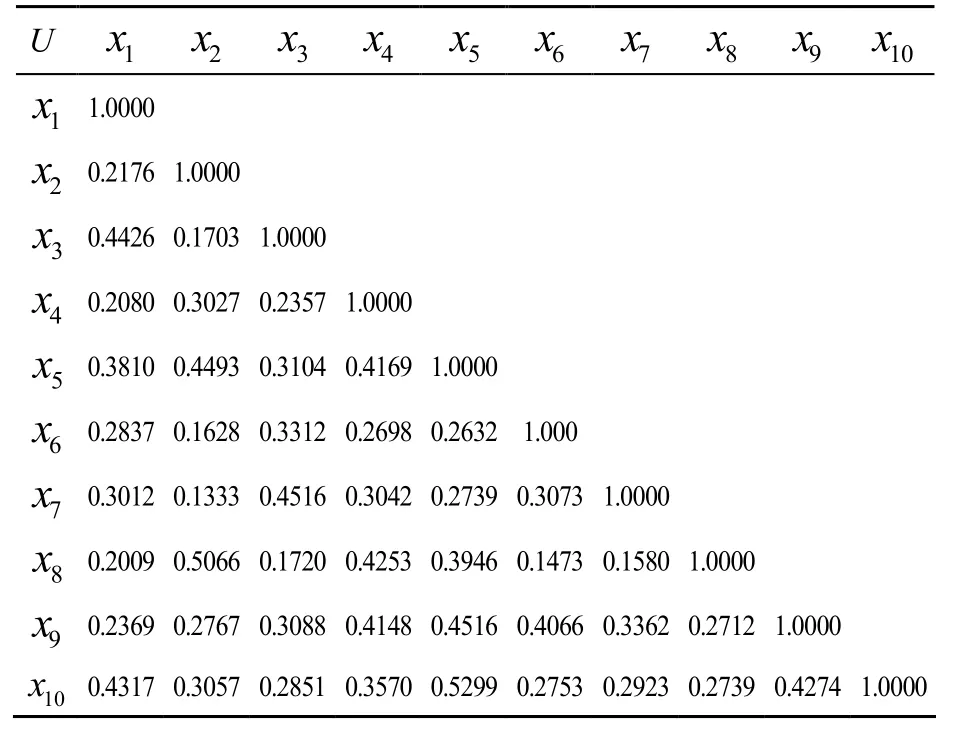
表2 U 上的模糊等价关系

3 结束语

粗糙集理论的发展与应用领域中将经典粗糙集理论推广到模糊关系是一个重要的研究方向。本文定义了在区间值模糊信息系统中的模糊等价关系通过模糊等价关系定义了粗糙隶属度。进而又得到了粗糙隶属度的重要性质并通过例子进行了证明。目前对于粗糙隶属度在其他信息系统中的研究还不全面。所以接下来就要在序信息系统中做进一步的探讨。

[1]Zadeh L A. Fuzzy Sets[J]Information and Control 19658：338-352.

[2]陈水利,李敬功,王向功. 模糊集理论及其应用[M]. 北京： 科学出版社,2006,1-196.

[3]Dubois D Prade H. Fuzzy Sets and Systems： Theory and Application.New York： Academic Press,1980,1-50.

[4]袁学海,李洪兴,孙凯彪. 直觉模糊集和区间值模糊集的截集、分解定理和表现定理[J]. 中国科学： 信息科学,2009,39(9)： 933-945.

[5]史德容,徐伟华. 区间值模糊决策序信息系统的分布约简[J]. 计算机科学与探索,2017,11(4)： 652-658.

[6]Pawlak Z. Rough Set [J]International Journal of Computer and Information Sciences,1982,11： 341-356.

[7]王兆浩 舒兰 丁修勇. 几种粗糙集模型的推广研究[J]. 计算机工程与应用 2011 47(36)：68-72.

[8]吉晨莉. 决策系统中属性约简的研究[D]. 西北师范大学,2013.

[9]Wu Weizhi Mi Jusheng Zhang Wenxiu. Generalized Fuzzy Rough Set[J].Information Sciences,2003,(5)： 263-281.

[10]张文秀,吴伟志. 基于随机集的粗糙集模型(I) [J]. 西安交通大学学报(自然科学版),2000,34(12)： 75-79.

[11]Zhang Xiaohong,Pei Daowu,Dai Jianhua. Fuzzy mathematics and the Rough set theory[M]. Beijing： Tsinghua university press,2012.1.

[12]Xu Weihua,Zhang Xiantao,Wang Qiaorong. Experimental computing on attribute by matlab in dominance-based variable precision rough set[J]. Journal of Chong Qing University of Technology,2013 No.1 Vol.27.

[13]李敏. 基于属性的粗糙集在数据挖掘中的应用[J]. 哈尔滨商业大学学报,2008,24(1)： 88-90.

[14]张腾飞,王锡淮,叶银忠. 粗糙集理论在故障诊断中的应用综述[J].上海海事大学学报200526(4)：20-26.

[15]李骞郑刚. 一种基于粗糙集的冠心病数据分类方法[J]. 天津理工大学学报,2007,23(1)： 70-74.

[16]徐伟华,刘士虎,张文修. 一般二元关系下基于粗糙隶属函数的程度粗糙集[J]. 重庆理工大学学报,2010,24(10)： 101-108.

[17]Lehmann .I Weber .R Zimmermann .H J. “Fuzzy set theory” OR Spectrum vol. 14 no.1 pp.1-9 1991.

[18]Dubois D Prade H. Rough fuzzy sets and fuzzy rough sets. International Journal of General Systems,1990,17(2-3)： 191-209.

Rough Membership Measure in Interval Valued Fuzzy Information System

ZHANG Jia,ZHANG Xiaoyan*,XU Weihua
(School of Science Chongqing University of Technology,Chongqing,400054,China)

Rough set theory of Pawlak. Z and interval valued fuzzy sets can be combined. On the basis of the existing concepts of interval valued fuzzy information systems the fuzzy approximation space is introduced according to the fuzzy equivalence relation. Moreover the similarity measure is given and the rough membership measure in interval valued fuzzy information system is defined by the similarity measure of any two objects in the fuzzy approximation space. Then the properties of rough membership measure are discussed in the paper.Finally an example is given to illustrate the feasibility and effectiveness of these properties.

Rough set theory; Interval value fuzzy information system; Fuzzy equivalence relation; Rough membership measure

TP18

A

1672-9129(2017)06-0008-04

10.19551/j.cnki.issn1672-9129.2017.06.003

张佳,张晓燕,徐伟华. 区间值模糊信息系统的粗糙隶属度[J]. 数码设计,2017,6(6)： 8-11.

Cite：ZHANG Jia,ZHANG Xiaoyan,XU Weihua. Rough Membership Measure in Interval Valued Fuzzy Information System[J]. Peak Data Science,2017,6(6)： 8-11.

2017-03-02。

国家自然科学基金（NO.61472463，NO.61402064），重庆市自然科学基金（No.cstc 2015jcyjA40053），重庆市研究生科研创新基金（NO.CYS16217，NO.CYS17281），重庆理工大学研究生创新基金（NO.YCX2015227，No.YCX2016227）资助。

张佳（1992-）女，山西阳泉，硕士研究生，研究方向：人工智能与粒计算；张晓燕（1979-）女，山西怀仁，博士副教授，硕士生导师，主要研究方向：不确定性推理；徐伟华(1979-），男，博士，教授，主要研究方向：粗糙集、不确定性推理与粒计算。

E-mail：zxy19790915@163.com