结构应变模态参数辨识的最小二乘复频域方法

周思达，曹博远，周小陈

（1.北京理工大学 宇航学院，北京 100081；2.北京理工大学 飞行器动力学与控制教育部重点实验室，北京 100081；3.北京理工大学 深空自主导航与控制工信部重点实验室，北京 100081；4.北京机电工程研究所，北京 100074）

结构应变模态参数辨识的最小二乘复频域方法

周思达1,2,3，曹博远1，周小陈4

（1.北京理工大学 宇航学院，北京 100081；2.北京理工大学 飞行器动力学与控制教育部重点实验室，北京 100081；3.北京理工大学 深空自主导航与控制工信部重点实验室，北京 100081；4.北京机电工程研究所，北京 100074）

由于应变模态对结构状态的敏感性，其在结构在线健康监测和损伤识别方面比位移模态更具优势。利用应变和位移的关系，将最小二乘复频域方法应用到结构应力应变分析中，建立基于应变测量数据的结构动力学参数频域辨识方法。由于应变模态和位移模态是同一种物理状态的不同表达形式，两者在数学表达上有相似性。首先建立以应变为变量的参数化公分母模型，在此基础上将非线性最小二乘问题进行线性化，得到加权线性最小二乘的方程误差。然后采用基于缩减正则方程的算法进行求解，减少计算量，并通过对模型参数施加约束来避免参数冗余。然后，设计并搭建一个自由梁的实验结构系统，利用光纤布拉格光栅应变传感器测量结构动应变数据，根据最小二乘复频域方法，基于应变测量数据辨识得到频率和阻尼比，与传统的基于加速度测量数据的辨识结果相吻合。另外，辨识所得应变模态振型与仿真结果也具有一致性。因此，数值仿真和实验验证表明，文中提出的基于最小二乘复频域方法能够准确辨识结构应变模态。

振动与波；应变模态；模态参数辨识；最小二乘复频域法；模态实验

基于模态测试技术的结构动态分析设计、损伤识别和健康监测得到了广泛深入的研究，并且在机械以及航空航天等领域取得了重要成果。传统的模态测试技术主要基于位移响应（或其关于时间的导数）的测量，但在工作状态下有时不便于测量结构的位移响应，如飞机机翼的变形、直升机桨叶的振动以及大型航天器结构的变形等。然而，基于应变响应的模态测试可以弥补传统模态测试技术的上述不足。另外，由于应变模态参数对结构状态的敏感性，其在结构损伤识别、在线健康监测、疲劳测试以及耐久性分析等方面比位移模态更具优势。光纤布拉格光栅（Fiber Bragg Grating，FBG）传感器能够实时测量结构动应变响应，与传统的位移传感器相比，具有质量轻、抗电磁干扰、便于多路复用等众多优点。近年来，随着光纤光栅传感技术的发展，FBG传感器在结构实时应变响应测量上的应用备受关注。若FBG传感器能取代传统的压电式位移传感器应用于航天器上，将有助于简化线路布局，减轻结构重量，增强抗电磁干扰能力，更好地监测航天器的结构健康状态。

目前，关于利用所测动应变响应数据进行应变模态参数辨识已有部分研究。自20世纪80年代起，人们就已经开始致力于研究直接用应变计来测量应变响应，从而建立应力应变响应预测模型。国内外学者将模态方法引入到应力、应变场中，已经取得了不少成果[1-2]。1979年日本学者村井等在位移响应计算公式中引入位移-应变转换系数来预测应变响应[3]。1984年，英国学者Hillary和Ewins应用电阻应变计测量了力-应变传递函数，并应用于激振力的识别，提出应变模态的概念[4]。我国学者伊立言曾用应变计测量了四边自由的矩形平板频率、阻尼和位移振型，并在位移传递函数的基础上，提出应变模态的概念[5]。此外，中美学者曾合作应用时域法分析梁的应变模态[6]。1988年，李德葆、夏苏等运用逻辑演绎法推导了应变频响函数矩阵的表达式[1]。1989年Bernasconi等[7]及1996年L.H.Yam等[8]同时运用位移模态微分运算方法推导和论述应变模态理论。清华大学的李德葆等着重对位移模态和应变模态间的关系进行了研究，推导了应变响应公式及应变频响函数矩阵，提出了模态试验与应变模态参数识别的方法，并采用仿真计算和实测进行比较验证[9]。2007年，Lae-Hyong Kang等利用位移和应变的关系，根据所测应变对梁的动态位移进行了估计[10]。2012年佛罗里达理工的Hao Jiang等根据梁理论推导了梁从应变模态到位移模态的转换关系，并对质量阶变的梁进行数值仿真和实验验证，实现了时变梁的弯曲振型的实时估计[11]。综上，以李德葆为代表的学者在从位移模态向应变模态转换方面建立了比较系统的理论，并在基于时域的辨识方法上成果颇丰。但时域方法易受噪声干扰，容易出现虚假模态。本文根据应变位移的关系，建立了应变格式的参数化结构动力学模型，利用最小二乘复频域方法来实现对应变模态参数的辨识，并通过实验对该方法进行了验证。

1 应变模态参数辨识的最小二乘复频域方法

1.1 应变格式的参数化结构动力学模型

物理坐标下，n自由度结构动力学系统的一般方程为

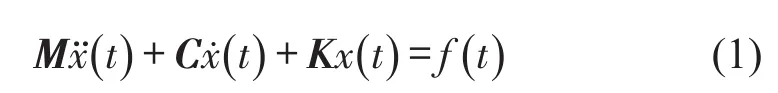
其中M为质量矩阵，C为阻尼矩阵，K为刚度矩阵，为外激励向量，分别为位移向量、速度向量和加速度向量。根据应变ε和位移x的关系，有

其中B为应变矩阵，是和被测结构有关的常系数方阵。因此，可得到应变格式的动力学微分方程

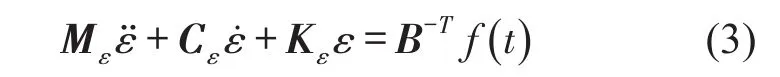
其中Mε=B-TMsB-1，Cε=B-TCsB-1，Kε=B-TKsB-1。

将式(3)进行Laplace变换，并假设初始速度和初始位移向量为零，则得到应变格式下Laplace域的系统运动方程

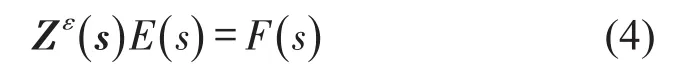
定义应变传递函数矩阵为

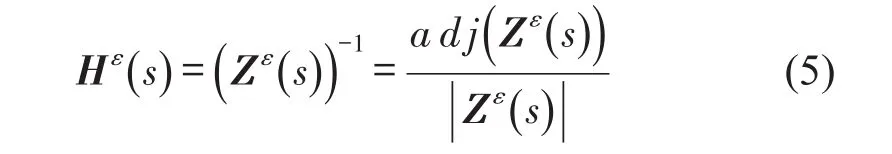
将式(5)进行模态分解，可得到基于应变的极点-留数模型

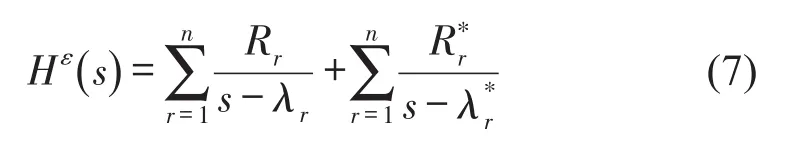
其中λr为第r阶应变模态的系统极点，Rr为第r阶应变模态的留数矩阵，且留数矩阵可分解为

其中Qr为模态比例因子，ψr为应变模态振型，φr为位移模态振型。

根据式(6)，线性时不变动力学系统的应变频率响应函数（第0个输出和第i个输入）可描述为

其中f=1,2,…,Nf为频率采样点数；k=1,2,…,NoNi（即k=(o-1)Ni+i），分子和分母均定义为多项式

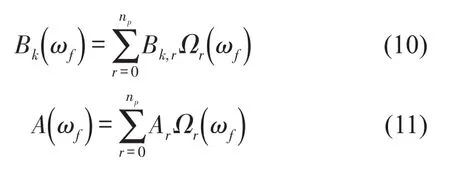
其中np为多项式的阶数；Bk,r和Ar为多项式系数；为广义的频率多项式基函数。在最小二乘复频域（Least Squares Complex Frequency-domain，LSCF）方法中，利用z域模型，从而基函数为

其中Ts为采样时间间隔。

多项式系数可以写成向量的形式

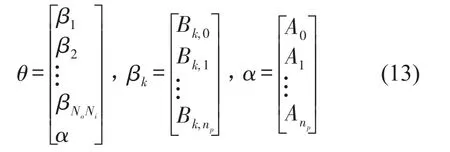
1.2 加权线性最小二乘的形式

非线性最小二乘的方程误差为

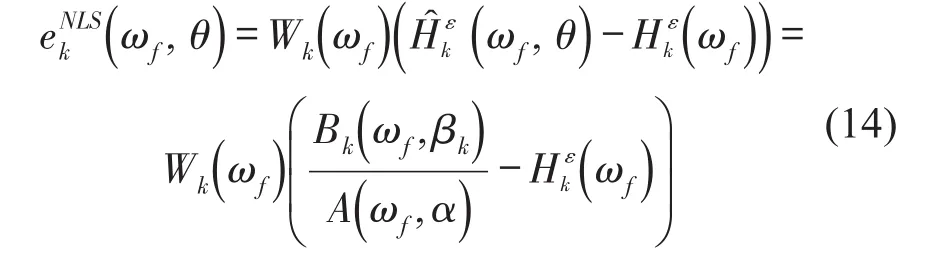
其中θ为待定的未知参数向量；为取决于频率和系统输出的权函数，反映不同输出之间可能存在的数据质量的误差；为应变频响函数；为应变频响函数的估计。

非线性最小二乘的费用函数（cost function）为

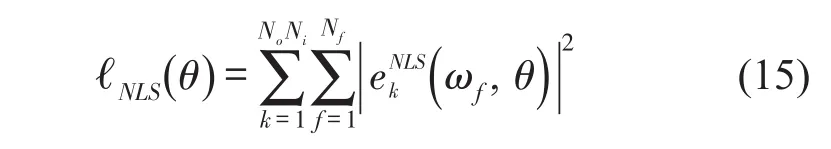
根据公分母模型，可以对应变频率响应函数为基本辨识参数的最小二乘问题进行线性化，即式(14)同乘A( )

ωf,α，得到（次优）线性最小二乘的方程误差

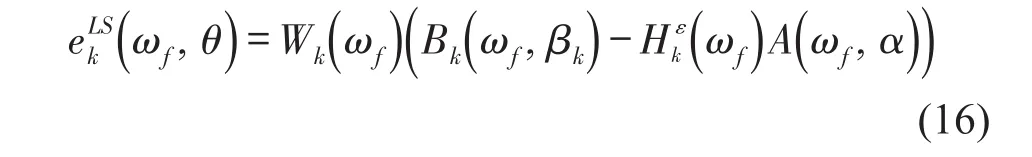
将方程误差写成矩阵形式

因此，线性最小二乘的费用函数为

其中Jacobi矩阵为

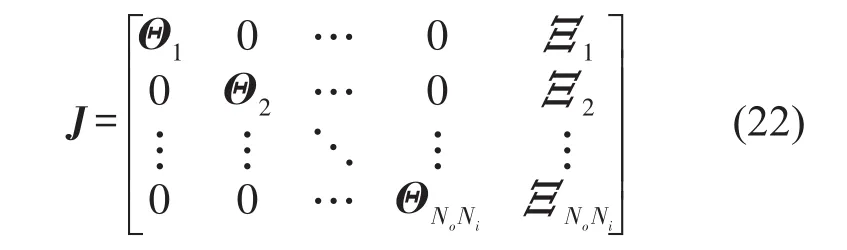
1.3 基于减缩正则方程的求解方法

本文采用基于缩减正则方程的算法来求解如式(21)所示的线性最小二乘问题，该方法不用求解规模庞大的Jacobi矩阵，而是对一个缩减的正则方程进行求解，大大减少了计算量。

式(21)的费用函数最小时，费用函数对未知参数的1阶导数为零，即

华北多特高压交直流强耦合大受端电网系统保护方案设计//罗亚洲,陈得治,李轶群,王青,张剑云,訾鹏,等//(22):11

将式(23)代入式(24)中，得

另外，式(9)所示的参数化模型是参数冗余的，若给定常数γ，则有

如式(26)的参数冗余将会导致缩减的最小二乘正则方程右端项为0，导致方程具有奇异解。因此，必须对模型参数施加约束，例如选取α中最后一个分量为1，则缩减的正则方程为

1.4 模态参数的计算

通过加权的线性最小二乘辨识可得到参数化模型中待估的未知参数向量θ。若θ确定，则可以确定应变频率响应函数的公分母模型。通过将公分母模型转换为极点-留数模型可得到结构的模态参数。

首先，通过求解含有系数α的公分母多项式A(ω,α)的根得到系统极点，从而利用系统极点得到结构的应变模态频率和应变模态阻尼比

接着，根据得到的系统极点和参数化的应变频率响应函数得到系统的各个输入输出对应的留数。

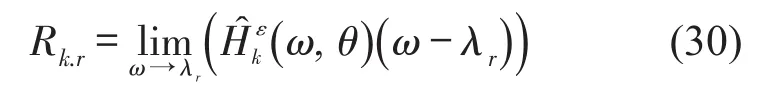
最后，通过留数矩阵计算应变模态振型。对留数矩阵进行奇异值分解（SVD）

假设系统满足模态叠加原理，则有

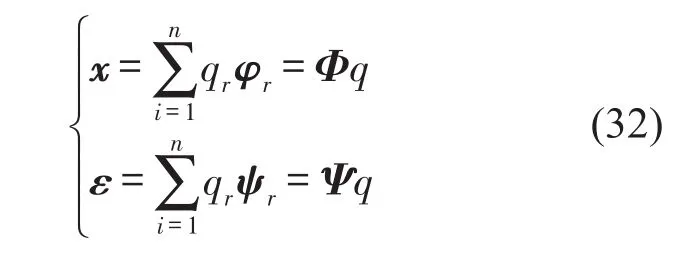
其中Φ为位移模态振型矩阵，Ψ为应变模态振型矩阵，q为模态坐标向量，则可得应变模态振型与位移模态振型间的关系

因此，应变模态振型与位移模态振型完全不相同。

1.5 仅输出模态参数的辨识

对于仅输出模态参数的辨识，结构动力学系统的激励（输入）信号未知，因此，上述用于辨识的测量的频率响应函数也是未知的。为将输入输出的频率模态参数辨识方法拓展到仅输出情况，通常采用结构响应的功率谱函数代替频率响应函数。当系统激励为白噪声时，其功率谱函数矩阵如下式

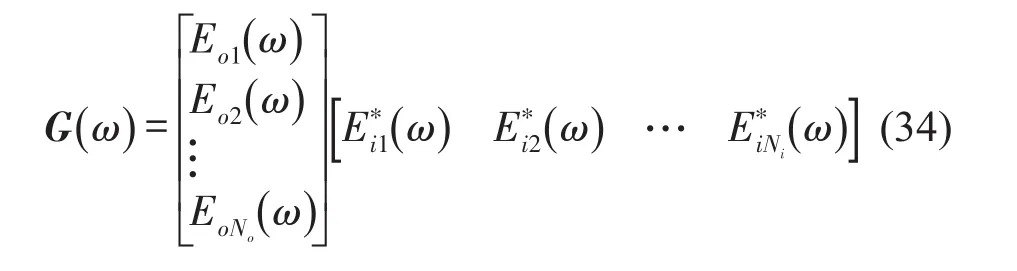
2 实验验证

2.1 实验结构及测试系统搭建

图1 实验装置及测试系统示意图

为验证上文提出的应变模态参数辨识算法，以一根钢制梁为测试结构进行实验验证，该梁的几何参数为：长L=2 000 mm，宽W=60 mm，厚度h=10 mm。实验结构及测试系统的搭建如图1所示，梁的几何参数与仿真模型相同，利用弹性橡皮绳将其竖直吊置以近似自由-自由约束，在梁的两侧分别均匀对应分布15个压电式加速度传感器和15个FBG传感器，从而在对梁施加激励时可以同时测得加速度数据和应变数据。其中，15个加速度传感器分别接入LMS公司的SCADASⅢ振动测试系统的15个通道以采集加速度信号；15个FBG传感器分成3条线路，每条线路按中心波长从小到大分布5个不同中心波长的FBG传感器，接入Micron Optics公司的SM130光纤光栅传感解调仪的3个通道，从而对FBG传感器的反射光波信号进行采集解调以获取动应变数据。激振器（ModalShop 2025E）用于输出不同类型的带宽信号或单频信号，对于该验证实验激振器施加白噪声激励，故可以认为此输入力信号未知。

实验装置的实物照片如图2所示，其中左侧为实验结构的整体图，右上为光纤光栅传感解调仪，右下分别为激振器与加速度传感器以及FBG传感器的局部放大图。

图2 实验装置实物图

2.2 实验结果

实验中，动应变的采样频率为1 000 Hz，采样周期为8 s，对输出信号加Hanning窗以避免泄露现象，将功率谱平均30次以减小噪声。利用本文提出的最小二乘复频域方法对采集的应变数据进行辨识，得到该钢制梁的应变模态辨识结果如表1所示，并与所测位移模态进行对比。

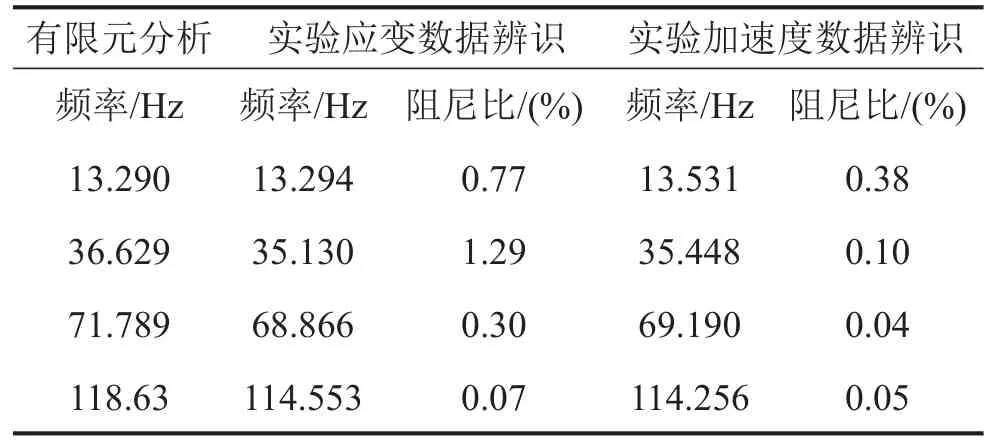
表1 实验辨识结果

由表1可看出，应变数据和加速度数据均可以准确地辨识出结构的模态参数，且与有限元分析的结果相吻合，因此，利用应变响应数据辨识系统的动力学参数是可以保证辨识精度的。但由于Hanning窗的影响，增加了数值阻尼，所以应变模态阻尼比较位移模态阻尼比偏大。

图3和图4分别为辨识出的前4阶应变模态振型与位移模态振型，并与对应的有限元分析的振型作对比。

图3 前4阶应变模态振型的辨识结果与有限元分析结果对比

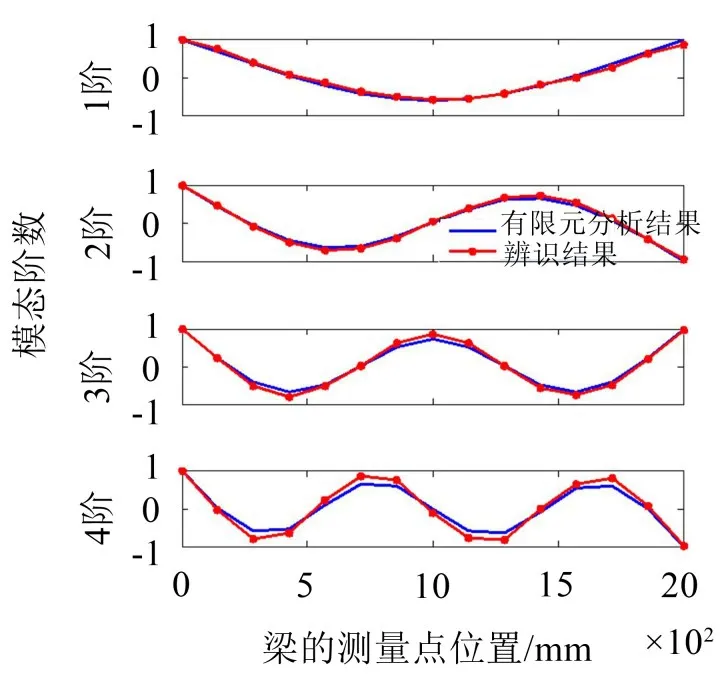
图4 前4阶位移模态振型的辨识结果与有限元结果对比

由图3可以看出，辨识出的前4阶应变模态振型与有限元计算出的振型相吻合，表明本文提出的应变模态辨识方法能够准确辨识结构的应变模态振型。另外，比较图3和图4发现，应变模态振型与位移模态振型是不同的，这与前面的推导结论一致。

图5为应变模态的模态判定准则（Modal Assurance Criterion，MAC），对角线数值接近1，非对角线数值接近0，说明本文所辨识出的前4阶应变模态振型具有很好的正交性。

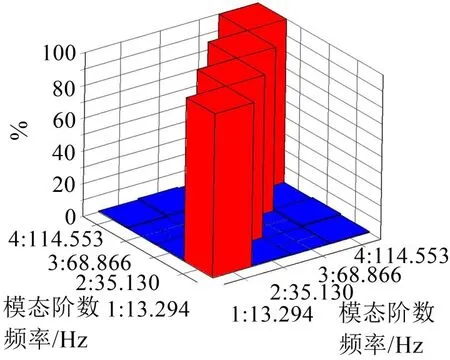
图5 应变模态的模态判定准则

3 结语

本文利用应变和位移的关系，应用最小二乘复频域方法建立了基于动应变测量数据的结构动力学参数频域辨识方法。通过建立以应变为变量的参数化的公分母模型，并在此基础上将非线性最小二乘问题进行线性化，得到加权线性最小二乘的方程误差，然后设计并搭建了一个自由梁的实验结构系统对本文的方法进行了验证。本文的总结与归纳如下：

(1)与传统压电式加速度传感器相比，FBG传感器质量轻，方便复用，可减轻结构质量，简化线路布局。

(2)利用应变与位移的关系，建立基于最小二乘复频域方法的结构应变模态参数辨识方法，该方法仅需用到系统应变响应输出，可应用于环境激励下结构应变模态参数的辨识。

(3)直接利用FBG传感器测得应变数据辨识出结构应变模态，避免了利用位移模态计算应变模态时的差分误差，因此应变模态参数在结构的在线损伤识别和健康监测等方面更具优势。

(4)实验结果表明，本文提出的基于最小二乘复频域方法的应变模态参数辨识方法能够准确辨识出结构的应变模态参数。

[1]李德葆.实验应变/应力模态分析若干问题的进展评述[J].振动与冲击，1996，15(l)：13-17.

[2]陆秋海，李德葆.模态理论的进展[J].力学进展，1996，26(4)：464-472.

[3]村井.动态设计分析的研究[J].小松技报，1979，25(2)：7-14.

[4]HILLARY B,EWINS D J.The use of strain gauges in force determination and frequency response function measurements[C].Proc.of 2nd IMAC,1984:627-634.

[5]伊立言.应变计在实验模态分析中的应用[C].第二届全国振动理论及应用会议，西安，1984.

[6]SONG T C,ZHANG P Q,FENG W Q,et al.The application of the time domain method in strain modal analysis[C].Proc.of 4th IMAC,1986:3-6.

[7]BERNASCONI O,EWINS D J.Application of strain modal analysis testing to real structures[C].Proc.of 7th IMAC,1989:1453-1464.

[8]YAM L H,LEUNG T P,LI D B,et al.Theoretical and experimental study of modal strain analysis[J].Journal Sound and Vibration,1996,191(2):251-260.

[9]李德葆，陆秋海.应变模态分析与曲率模态分析[C].现代振动与噪声技术，2001：149-167.

[10]KANG LAE-HYONG,KIM DAE-KWAN,HAN JAEHUNG.Estimation of dynamic structural displacements using Fiber Bragg Grating strain sensors[J].Journal of Sound and Vibration,2007,305(3):534-542.

[11]JIANG H,VAN DER VEEK B,KIRK D,et al.Real-time estimation of time-varying bending modes using fiber Bragg grating sensor arrays[J].AIAA Journal,2013,51(1):178-185.

Least Square Complex Frequency-domain Method for Structural Strain Modal Parameter Identification

ZHOU Si-da1,2,3,CAO Bo-yuan1,ZHOU Xiao-chen4
(1.School ofAerospace Engineering,Beijing Institute of Technology,Beijing 100081,China;2.Key Laboratory of Dynamics and Control of Flight Vehicle,Ministry of Education,Beijing 100081,China;3.Key Laboratory ofAutonomous Navigation and Control for Deep Space Exploration,Ministry of Industry and Information Technology,Beijing 100081,China;4.Beijing Electro-mechanical Engineering Institute,Beijing 100074,China)

Due to its sensitivity to structural state,the strain mode has more advantages than the displacement mode in online structural health monitoring and damage identification.Since the strain mode and displacement mode are merely the different expressions of the same physical state and they are similar in mathematical expression,the relationship between strain and displacement can be applied to the least square complex frequency-domain method(LSCF)to analyze structural stress and strain.In this study,the frequency domain identification method of structural dynamics parameters is established based on strain measurement data.First of all,a parameterized common denominator model with strain as its variable is established.On this basis,the nonlinear least square problem is linearized and the error of the weighted least square linear equation is obtained.Then,the equation is solved by using the algorithm based on the reduction of regular equations.In this way the amount of computation is reduced and parameter redundancy is avoided by imposing the restriction on the modal parameters.Afterwards,an experimental system of a free beam structure is designed and the structural dynamic strain is measured using Fiber Bragg Grating strain sensors.Finally,the frequency and damping ratio are identified by means of LSCF based on the measured strain data.The acceleration results of the identification agree well with those of the traditional identification method based on the measurement data of acceleration.Besides,the strain mode shapes obtained by this identification method are also consistent with the simulation results.Therefore,numerical simulation and the experiment show that the proposed method based on LSCF can accurately identify the strain modes of structures.

vibration and wave;strain mode;modal parameters identification;LSCF;modal experiment

V214.1；TH113.1

A DOI编码10.3969/j.issn.1006-1355.2017.06.004

1006-1355(2017)06-0017-06

2017-02-28

国家自然科学基金资助项目（11402022）

曹博远（1992-），男，石家庄市人，硕士研究生，主要研究方向为应变模态参数辨识与实验。

周思达，男，硕士生导师。E-mail:zhousida@bit.edu.cn