两种多天线GNSS动态定姿方法的比较

蔡小波，许厚泽，柴 华，丁磊香，王 勇

（1.中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室，武汉430077；2.中国科学院大学，北京100049）

两种多天线GNSS动态定姿方法的比较

蔡小波1，2，许厚泽1，柴 华1，丁磊香1，2，王 勇1

（1.中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室，武汉430077；2.中国科学院大学，北京100049）

针对移动载体对姿态的需求，对两种多天线GNSS动态定姿方法，即直接法和最小二乘迭代法进行了研究。分析了定姿的原理，给出了姿态解算模型。基于车载四天线GNSS的实测数据，分别用两种方法进行了姿态解算，并用同一运动平台高精度惯导给出的姿态作为参考值，对两种定姿方法的精度和可靠性进行了分析和比较。

多天线GNSS；动态定姿；基线；最小二乘迭代

0 引言

在一些特殊的载体上，如车载的移动测量系统或机载的对地观测系统等均需要确定载体的姿态［1-2］。在移动矢量重力测量系统中，为了提高矢量重力水平方向的测量精度，也需要高精度的姿态信息［3］。为了获取载体的姿态，最常见的是利用惯性导航系统（INS）或其与全球导航卫星系统（GNSS）组成的组合导航系统。然而，这类系统存在着成本高、姿态误差会随时间积累等不足［4-5］。近年来，随着 GNSS技术的完善，利用多天线GNSS定姿的方法越来越受关注［6-8］。与INS相比，多天线GNSS定姿成本更低，应用更加灵活，并且姿态误差不随时间积累，具有一定的优势。

多天线GNSS定姿时，一般先解算天线间的动态基线，然后再利用动态基线进行定姿［9-10］。由动态基线定姿的方法主要有直接法和最小二乘迭代法［11-12］。直接法是直接利用天线间的动态基线在导航坐标系各轴上的坐标分量解算载体的姿态，利用一条基线可以解算航向角和俯仰角，利用两条基线即可解算全部的3个姿态角［12］。最小二乘迭代法是在每个历元利用各基线向量在载体坐标系和导航坐标系的坐标分量，在已知载体初始姿态的情况下，利用迭代法对载体的真实姿态进行逼近［11-13］。与直接法相比，最小二乘迭代法可以利用更多天线的数据。本文对这两种定姿算法进行了研究，分别给出了两种方法的姿态解算模型。为了检验两种定姿方法的有效性，基于车载的四天线GNSS实测数据，分别用两种方法进行了姿态解算，并用同平台的高精度INS给出的姿态作为参考值，对两种定姿方法的精度和可靠性进行了评估，并对各自的优缺点进行了比较分析。

1 动态定姿模型

载体的姿态是指与载体固联的载体坐标系相对于导航坐标系的取向，姿态一般用姿态矩阵和姿态角表示。载体坐标系至导航坐标系的坐标变换矩阵称为载体的姿态矩阵，姿态角表示导航系旋转至载体系时绕3个坐标轴旋转的角度。姿态矩阵和姿态角之间的关系可表示为［12］：

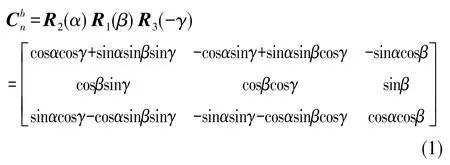
在利用多天线GNSS进行定姿时，多基于天线组构成载体坐标系，如图1所示。天线1为主天线，天线1与天线2的连线与载体纵轴平行，构成载体坐标系的Yb轴，天线1与天线4的连线与载体横轴平行，构成载体坐标系的Xb轴，构建如图1所示的载体坐标系O－XbYbZb。

1.1 直接法

由于直接法只需2条基线，即3副天线，就可解出全部的3个姿态角。本文基于天线1、天线2和天线3给出直接法定姿的模型，天线1、天线2和天线 3在载体系的坐标分别为（0，0，0）、（0，L12，0）、（L13sinθ，L13cosθ，0）。

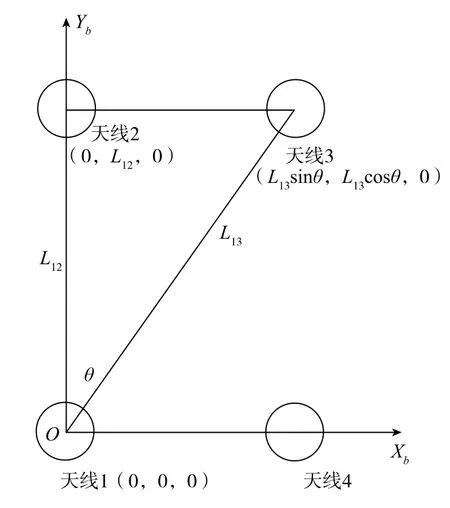
图1 载体坐标系及天线示意图Fig.1 Illustration of body-frame and antenna

在每个观测历元，通过精密单点定位（PPP）可以获得天线1在地固系的坐标，通过动态基线解算可以获得地固系下天线1至天线2、天线1至天线 3 的基线向量，分别记为s12，e、s13，e：

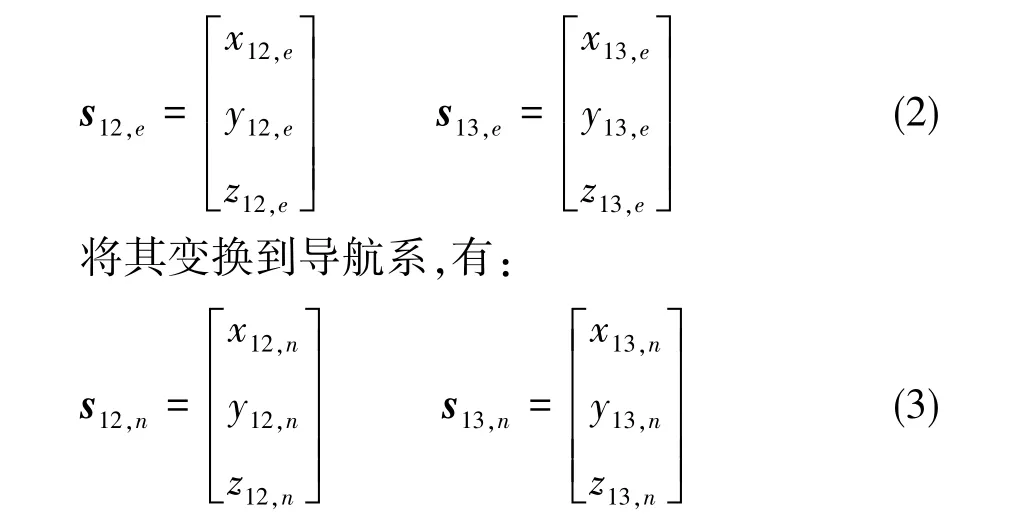
两条基线在载体坐标系的坐标记为：

天线1至天线2的基线向量在载体系和导航系的坐标之间的关系为：

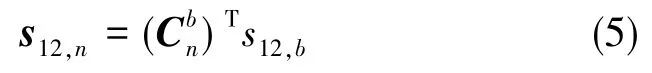
将式（3）、式（4）代入式（5），可解航向角为：

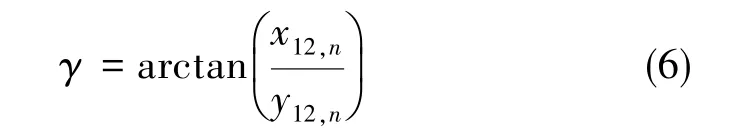
俯仰角为：

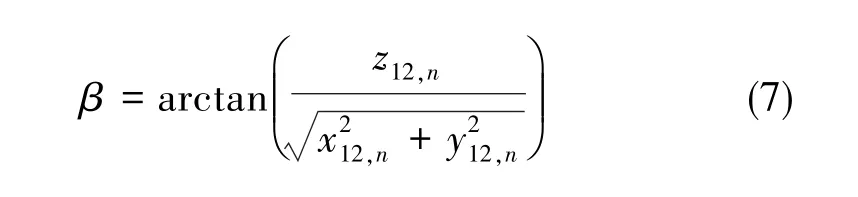
天线1至天线3的基线向量在载体系和导航系的坐标之间的关系为：

将式（3）、式（4）代入式（8），可解得横滚角为：

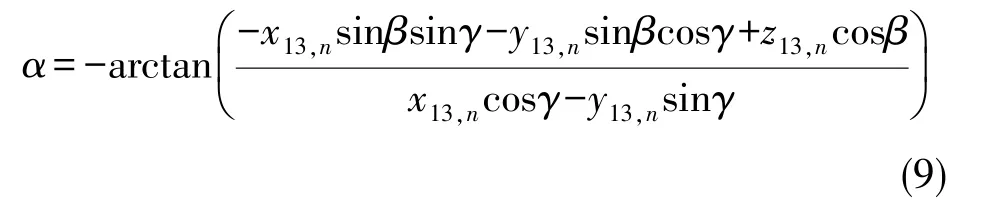
1.2 最小二乘法迭代法

如果天线数多于3个，为了更充分地利用观测数据，需要利用最小二乘法进行姿态解算。姿态矩阵含有9个元素，但只有3个独立的参数，即3个姿态角α、β和γ，最小二乘迭代法将这3个参数作为未知变量进行求解。第i个天线相对于天线1的基线向量在载体系和导航系的投影之间的关系为：

式中，t表示天线数；s1i，n、s1i，b为观测值；α、β和γ为未知参数，基于近似值α0、β0和γ0。对式（10）作线性化得：

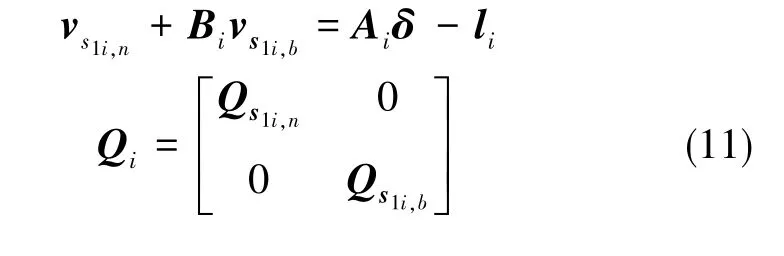
式中，Qi为观测值（s1i，n，s1i，b）的协方差矩阵，其余各符号分别表示为：

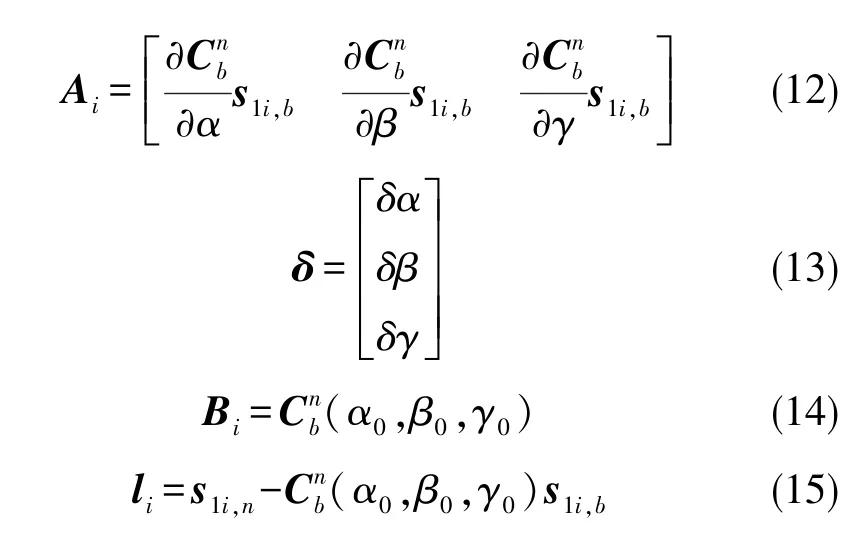
联合所有天线的观测数据，通过间接平差原理可得：

则姿态角的估值为：

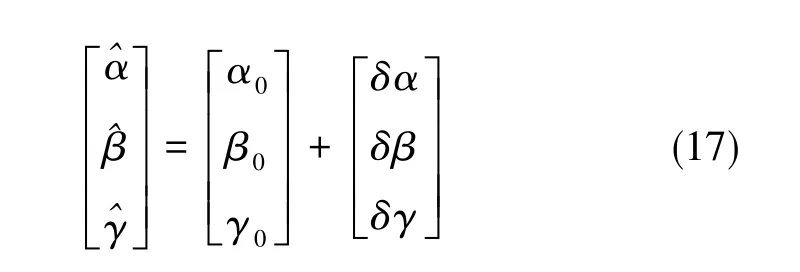
协方差矩阵为：

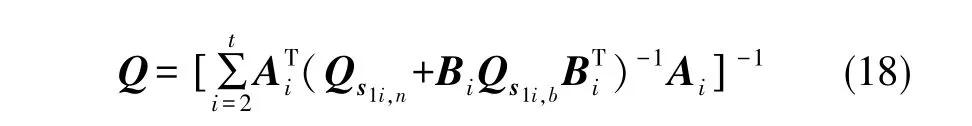
得到δ后判断其值是否大于阈值，若大于阈值，则将姿态估值作为近似值再次进行计算，直到δ小于阈值。最小二乘迭代法能充分利用天线组所包含的全部信息，姿态角的估值也是最优的，但计算复杂，需要进行迭代计算。

2 实验与结果分析

实验时用一辆实验车搭载一套采样频率为1Hz的4天线GNSS用于姿态测量，同时车内搭载一套高精度的INS，陀螺漂移为0.006（°）/h，采样频率为200Hz，用于提供姿态参考值。4副GNSS天线按照图1所示固定于车顶，天线1和天线2之间的基线长度为2.641m，天线1和天线3之间的基线长度为2.820m，天线1和天线4之间的长度为1.053m。实验共采集了45min的动态观测数据，车速保持在40km/h左右。

2.1 姿态解算

直接法利用天线1、天线2和天线3的数据进行姿态解算。先利用精密星历和精密钟差解算天线1的地固系坐标，以及天线1至天线2和天线1至天线3之间的动态基线在地固系下的坐标。然后，利用天线1的WGS84坐标将两条基线向量的坐标变换到导航系。基于导航系下的基线坐标，即可进行载体姿态解算。

最小二乘迭代法利用4个天线的数据进行姿态解算，与直接法姿态解算不同的是，最小二乘迭代法需要利用载体系下的基线向量。于是先通过静态观测数据解算出4天线之间全部基线的长度，从而解得天线2、天线3和天线4在载体系的坐标。姿态解算时，先给定姿态角的初始值，利用导航系下和载体系下的基线坐标，对3个姿态角进行迭代计算。两种方法解得的姿态角与高精度INS给出的参考值如图2所示。

从图2可以看出，在动态条件下，两种方法都能很好地捕捉到载体姿态的变化，并与高精度INS给出的姿态参考值符合较好。

图2 两种方法解得的姿态角与高精度INS的比较Fig.2 Comparison of the attitude angle determined from the two methods and INS

2.2 结果分析与比较

从姿态解算过程可以看出：直接法计算简便，不需要测量天线在载体坐标系的坐标，姿态解算过程中也不需要进行矩阵求逆；缺点是只能处理3天线的数据，不能获得最优解。最小二乘迭代法可以同时利用更多天线的数据，并可以获得最优解，但是需要利用天线在载体系的坐标，计算过程中需要矩阵求逆，在某些动态条件下存在奇异性问题。取高精度INS给出的姿态作为参考值，在消除系统差之后，两种方法定姿的误差如图3～图5所示，误差统计如表1所示。

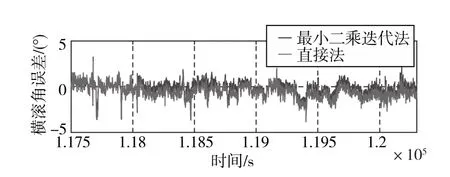
图3 两种方法解得的横滚角误差比较Fig.3 Comparison of the errors of the roll angle determined from the two methods

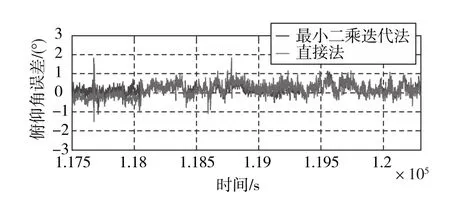
图4 两种方法解得的俯仰角误差比较Fig.4 Comparison of the errors of the pitch angle determined from the two methods

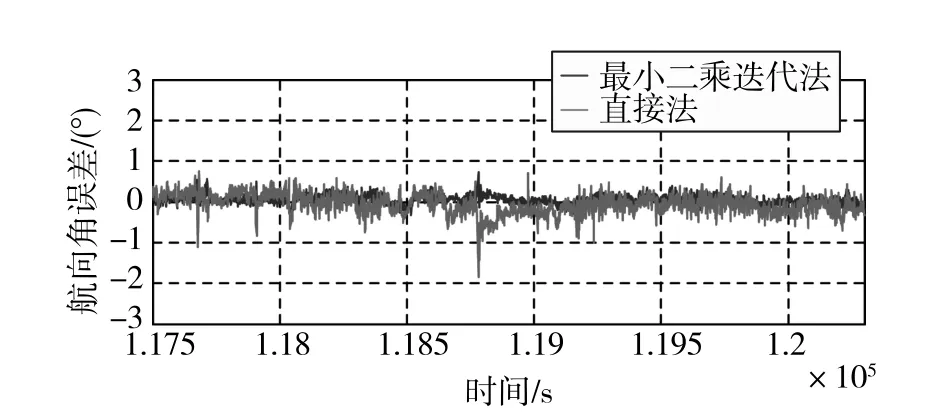
图5 两种方法解得的航向角误差比较Fig.5 Comparison of the errors of the yaw angle determined from the two methods

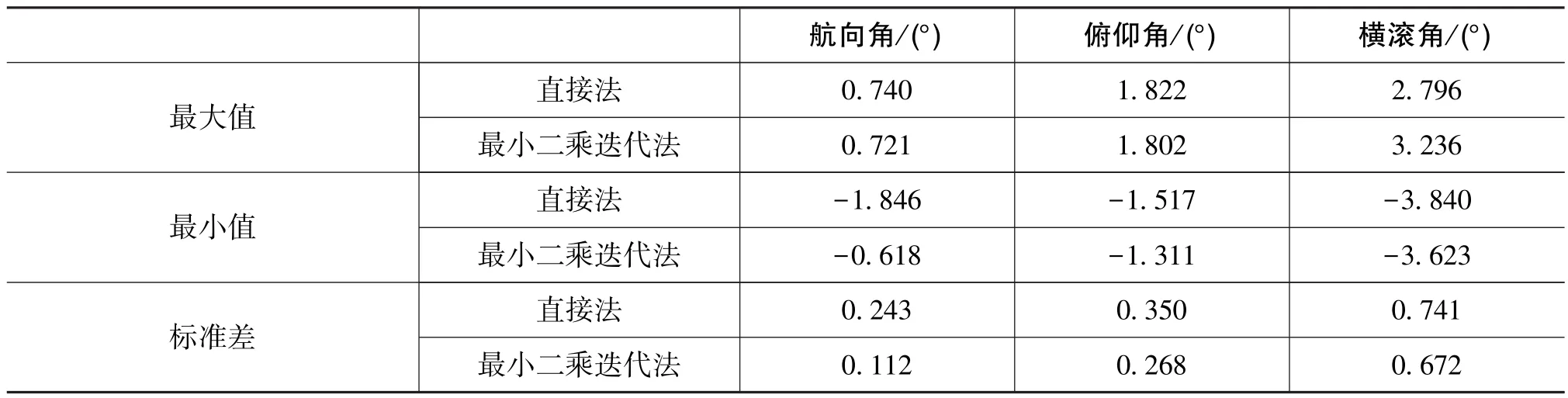
表1 直接法和最小二乘迭代法的精度比较Table 1 Comparison of the attitude precision determined from the direct method and the least square iterative method

从图3～图5及表1可以看出，最小二乘迭代法由于利用了4个天线的数据，姿态解算的精度要高于直接法，可靠性也高于直接法。然而，最小二乘迭代法在迭代计算时对初始姿态有较强的依赖，如果初始姿态精度较差，则最小二乘迭代法并不能提高姿态估计精度。在初始姿态精度过差的时候，迭代还会发散，得不到姿态的正确估值。

多天线GNSS定姿的精度主要与动态基线解算精度有关，除此之外还与天线布局有关。经分析可知，俯仰角的精度与基线长度L12成反比，与俯仰角的余弦成反比，基线长度L12越长，俯仰角越接近于0，航向角的精度越高；俯仰角的精度与基线长度L12成反比，基线长度L12越长，俯仰角的精度越高；横滚角的精度与基线长度L13和θ成反比，基线长度L13越长，横滚角精度越高，且当基线长度一定时，θ＝90°对于提高横滚角的精度最为有利。

3 结论

本文研究了两种基于多天线GNSS的动态定姿方法，给出了两种方法的定姿模型，并对基于4天线的实测数据进行了处理。处理结果表明，在较短基线条件下，通过两种方法均能获得高精度的姿态信息，且最小二乘迭代法的精度稍高于直接法。因此在利用多天线GNSS定姿时，采用基于4天线的最小二乘迭代法解算得到的姿态具有更高的精度和可靠性，在条件有限时，采用基于3天线的直接法定姿亦可达到较高的精度。

[1]Madeira S，Gonçalves J，Bastos L.Accurate DTM generation in sand beaches using mobile mapping[J].Journal of Coastal Conservation，2013，17（3）： 579-588.

[2]Kukko A，Kaartinen H，Hyyppä J，et al.Multiplatform mobile laser scanning：usability and performance[J].Sensors，2012，12（9）： 11712-11733.

[3]柴华，王勇，王虎彪，等.GNSS/SINS组合进行惯性重力测量误差分析[J].大地测量与地球动力学，2011，31（6）： 73-78.CHAI Hua，WANG Yong，WANG Hu-biao，et al.Error analysis for inertial gravimetry by use of GNSS/SINS combination[J].Journal of Geodesy and Geodynamics，2011，31（6）： 73-78.

[4]Liu S，Sun F，Zhang L，et al.Tight integration of ambiguity-fixed PPP and INS：model description and initial results[J].GPS Solutions，2016，20（1）： 39-49.

[5]吴富梅，聂建亮，何正斌.低成本车载GPS/INS组合导航姿态角更新算法[J].中国惯性技术学报，2010，18（6）： 675-679.WU Fu-mei，NIE Jian-liang，HE Zheng-bin.Low-cost GPS/INS integrated navigation algorithm in land vehicle system considering attitude update[J].Journal of Chinese Inertial Technology，2010，18（6）： 675-679.

[6]Rabbou M A，El-Rabbany A.Tightly coupled integration of GPS precise point positioning and MEMS-based inertial systems[J].GPS Solutions，2015，19（4）： 601-609.

[7]Hide C，Pinchin J，Park D.Development of a low cost multiple GPS antenna attitude system[C].The 20thInternational Technical Meeting of the Satellite Division of The Institute of Navigation，Manassas VA，2007.

[8]Aleshechkin A M.Algorithm of GNSS-based attitude determination[J].Gyroscopy and Navigation，2011，2（4）：269-276.

[9]刘根友，欧吉坤.GPS单历元定向和测姿算法及其精度分析[J].武汉大学学报（信息科学版），2003，28（6）：732-735.LIU Gen-you，OU Ji-kun.Determining attitude with single epoch GPS algorithm and its precision analysis[J].Geomatics and Information Science of Wuhan University，2003，28（6）： 732-735.

[10]高源骏.GPS测姿算法与天线布局研究[D].哈尔滨工程大学，2011.GAO Yuan-jun.Research on GPS attitude determination algorithm antenna configuration[D].Harbin Engineering University，2011.

[11]Ballal T，Bleakley C J.GNSS instantaneous ambiguity resolution and attitude determination exploiting the receiver antenna configuration[J].IEEE Transactions on Aerospace and Electronic Systems，2014，50（3）： 2061-2069.

[12]何海波.高精度GPS动态测量及质量控制[D].解放军信息工程大学，2002.HE Hai-bo.Precise kinematic GPS surveying and quality control[D].The PLA Information Engineering University，2002.

[13]王冰，隋立芬，张清华，等.利用GPS解算载体测姿的算法研究[J].武汉大学学报（信息科学版），2013，38（12）：1392-1395.WANG Bing，SUI Li-fen，ZHANG Qing-hua，et al.Research on attitude determination algorithms using GPS[J].Geomatics and Information Science of Wuhan University，2013，38（12）： 1392-1395.

The Comparison of Two Dynamic Attitude Determination Methods Based on Multi⁃antenna GNSS

CAI Xiao-bo1，2，XU Hou-ze1，CHAI Hua1，DING Lei-xiang1，2，WANG Yong1
（1.State Key Laboratory of Geodesy and Earth's Dynamics，Institute of Geodesy and Geophysics，Chinese Academy of Sciences，Wuhan 430077； 2.University of Chinese Academy of Sciences，Beijing 100049）

In view of the demands of attitude in mobile systems，two attitude determination methods based on the multi-antenna global navigation satellite system（GNSS），the direct method and the least square iterative method are researched.The principles of the attitude determination are analyzed and the models are derived.The data from a test on a land vehicle which used four-antenna are processed by the two methods.The attitude from a high-accuracy inertial navigation system（INS）on the same platform is used as reference，and the accuracy and reliability of the two attitude determination methods are evaluated and compared.

multi-antenna GNSS；dynamic attitude determination；baseline；the least square iterative

U666.1

A

1674-5558（2017）01-01338

10.3969 /j.issn.1674-5558.2017.06.004

2016-11-25

国家自然科学基金（编号：41274084）

蔡小波，男，博士，大地测量学与测量工程专业，研究方向为惯性导航及组合导航。