晃动环境下组合导航系统精度事后评估算法研究

陈维娜，曾庆化，刘建业，王慧哲

（南京航空航天大学导航研究中心，南京211106）

晃动环境下组合导航系统精度事后评估算法研究

陈维娜，曾庆化，刘建业，王慧哲

（南京航空航天大学导航研究中心，南京211106）

海风、波浪、海流等因素会产生舰船的摇摆晃动，从而给舰船导航系统精度带来严重干扰。固定区间平滑滤波处理算法能够利用观测时间间隔内全部观测信息得到状态的最小方差估计，对导航精度进行事后评估。在研究晃动环境下的SINS/GPS组合导航应用平滑滤波算法的相关原理的基础上，首先利用Kalman滤波器进行组合导航，存储相关信息后按时间逆序利用固定区间平滑滤波算法进行事后分析。该方法可以针对不同的海况以及不同的海上作业需求，有效地为组合导航系统精度提供检验标准，考核各种海洋环境下的导航系统精度。

组合导航；Kalman滤波；固定区间；最优平滑

0 引言

当舰船处于晃动环境时，由于风浪作用将产生摇摆及振荡运动，舰船运动在波浪载荷和风载荷的作用下也具有随机性。海风除了引起风载荷外，还会使海平面升高，波浪和海流也会对载体的稳定性和结构可靠性产生影响［1］。在这样的情况下，惯性测量单元中的陀螺和加速度计的测量精度也就受到严重影响。所以，在舰船运动过程中，通常需要获得载体的高精度导航参数以便对各种海况下的导航系统进行性能分析和考核，而这依赖于对实时导航数据进行事后评估［2］。因此，针对晃动环境下的组合导航数据精度进行事后分析和处理具有十分重要的现实意义和应用价值。

在晃动环境下，组合导航系统虽然弥补了单一导航系统的缺陷，利用Kalman滤波技术发挥了二者的长处［3］；但是，Kalman滤波只利用了当前时刻及以前的观测信息。为了进一步分析晃动环境下的传感器性能，获得更高精度的舰船运动参数，分析和评估单个传感器及组合系统的导航精度，采用固定区间平滑滤波处理算法对组合导航信息进行事后融合，从而为改进导航系统的性能提供依据。固定区间平滑滤波利用了观测时间间隔内全部观测信息来得到状态的最小方差估计，反映了组合导航系统在理想情况下能够达到的潜在精度［4-5］。本文主要围绕组合导航系统在晃动环境下的事后精度评估问题展开研究，建立了惯性/卫星组合导航系统状态和观测模型，并对晃动环境下的组合导航事后精度评估方案进行设计，最后通过仿真分析验证了本文所提出方法的有效性。

1 舰船在晃动环境下的运动模型

在晃动环境下，舰船受海风、海浪和海流等影响，会引起甲板的摇摆和摇荡运动，从而对舰船的组合导航系统精度产生影响。

舰船的运动一般由两部分组成，即舰船沿航向正常行驶运动以及由于海风、海浪等作用下造成的舰船不规则运动。当舰船处于晃动环境下时，可以近似为两个正弦波组合构成一个余弦波来描述晃动产生的俯仰、横滚、航向以及垂荡、纵荡、横荡［6］。

典型海况下的摇摆模型为：

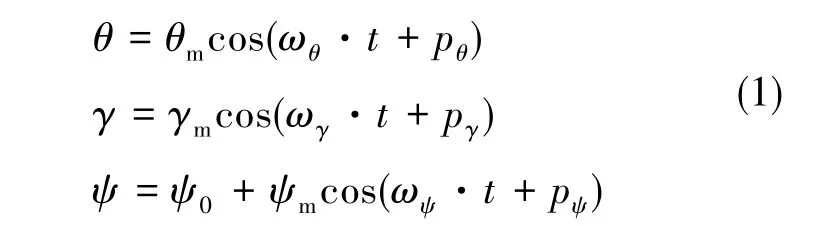
式中，θm、γm、ψm为俯仰、横滚与航向摇摆角的幅值，ωi（i＝θ、γ、ψ）为俯仰、横滚与航向摇摆角频率，pi（i＝θ、γ、ψ）为俯仰、横滚与航向初始相位，ψ0为航向初始方位角。

由垂荡、纵荡与横荡引起的线速度数学模型为：

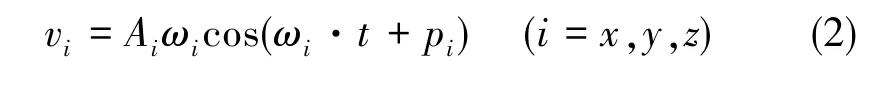
式中，Ai为垂荡、纵荡与横荡线速度幅值；ωi为垂荡、纵荡与横荡线速度角频率；pi为垂荡、纵荡与横荡线速度初始相位，且在 ［0，2π］上服从均匀分布的随机相位。

2 晃动环境下的事后精度评估方案设计

本文设计的晃动环境下舰船组合导航事后数据分析算法包括2个过程：先针对晃动环境设计舰船航迹，然后按时间顺序利用SINS/GPS组合导航数据信息进行实时Kalman滤波，滤波过程中存储有关信息。当滤波结束后，按时间逆序作固定区间平滑滤波处理。平滑处理的结果反映了系统在理想情况下能达到的潜在精度，从而可以对组合导航系统进行事后分析。晃动环境下的舰船组合导航系统事后处理算法结构图如图1所示。

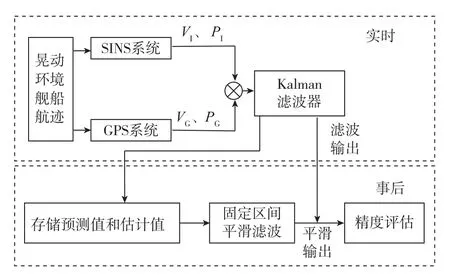
图1 晃动环境下GPS/SINS组合导航系统最优固定区间平滑仿真结构图Fig.1 Structure chart of fixed interval smoothing algorithm of GPS/SINS integrated navigation system in the shaking environment

2.1 组合导航系统状态方程

惯性系统作为整个组合导航系统的基本参考系统，导航坐标系选为东北天地理坐标系。对于捷联惯导系统，考虑到有陀螺仪随机漂移误差和加速计的零偏误差，通常将它们（陀螺漂移和加速度计零偏）扩充为状态向量的一部分，以更好地估计惯性器件的误差。系统的状态方程为：

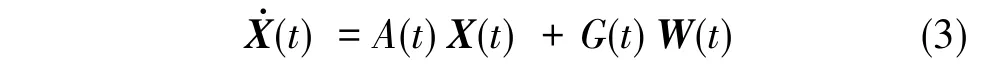
系统状态矢量X为：

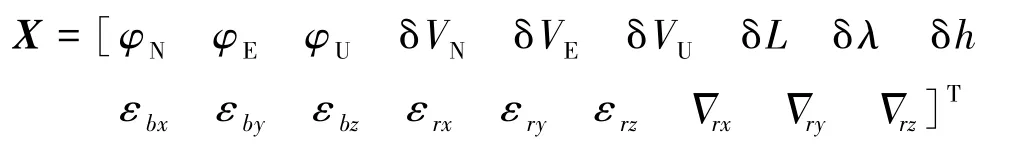
它包括9维惯导系统导航参数误差和9维惯性仪表误差。 其中，φE、φN、φU为平台误差角，δVE、δVN、δVU为东北天方向的速度误差，δL、δλ、δh为纬度、经度、高度位置误差，εbx、εby、εbz为陀螺仪随机常数，εrx、εry、εrz为陀螺仪1阶马尔柯夫过程，为加速度计1阶马尔柯夫过程［7］。

2.2 组合导航系统观测方程

在SINS/GPS组合导航系统中采用位置、速度组合模式，并选择惯性导航系统的误差方程为Kalman滤波的状态方程。在此条件下的量测方程有两组，其中位置量测差值由SINS给出的位置信息（经度、纬度、高度信息）与GPS接收机计算出的相应的位置信息求差，速度量测差值由SINS给出的速度信息与GPS接收机给出的相应速度信息求差［8］。

位置量测矢量定义如下：

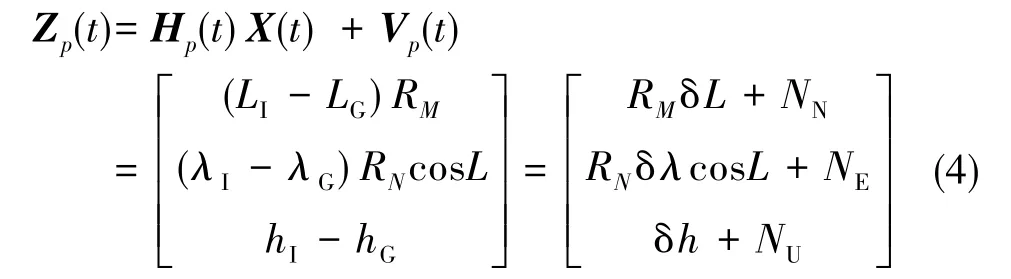
速度量测矢量定义如下：

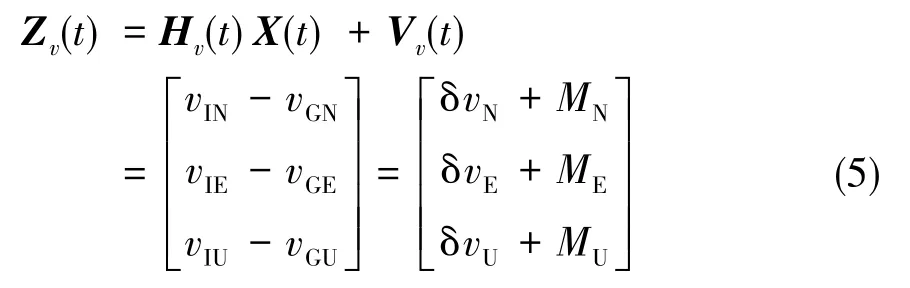
将式（4）和式（5）合并，得：

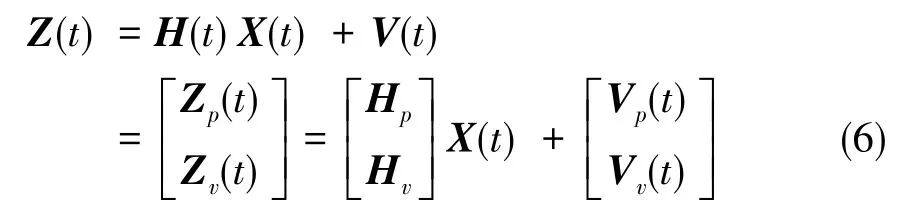
式（6）为SINS/GPS位置、速度组合模式的量测方程。其中，V1（t）为GPS位置、速度量测噪声矢量。

2.3 固定区间最优平滑算法研究

采用事后信息融合的方法可以进一步提高数据融合的精度，固定区间最优平滑滤波算法利用了被估计状态以后适合的量测值来估计，通过增加量测值的方法，以进一步提高系统的估计精度［9］。

假设Kalman滤波的离散状态方程和量测方程为：

假设系统的导航时间为[0→N]，在执行固定区间最优平滑滤波前，首先在整个时间区间内对式（7）所示的离散系统进行Kalman滤波，同时存储各个时刻的实时状态估计值、状态预测值、实时误差估计协方差阵和预测误差估计的协方差阵滤波结束后，按时间逆序作Kalman平滑处理。首先初始化平滑器，令k＝N，然后在[N－1→0]的固定区间内使用平滑算法，其递推公式如下所示。

平滑增益：

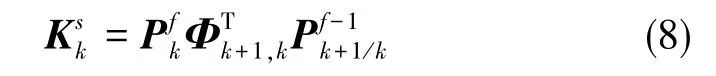
平滑的状态向量和方差阵的更新：

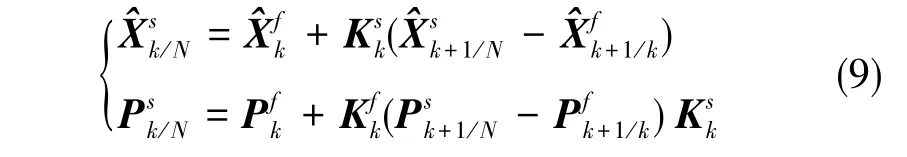
因此，固定区间平滑算法递推公式是一个由k＝N－1到k＝0的倒推过程，即为经过平滑滤波的结果。由于前向滤波数据处理过程已经消除了大部分的误差，再将滤波结果作为后向平滑的初始值，这种方法通过增加量测值提高了系统的估计精度。

3 系统仿真

在海洋环境中，由于水波和舰体本身速度和机动性能的影响，舰载动态环境有着自身的特点，下文将针对晃动环境下的固定区间最优平滑算法进行仿真对比研究。首先搭建系统仿真平台，包括捷联惯导和GPS仿真系统，然后利用Kalman滤波器实时进行组合导航，最后存储有关信息并进行事后固定区间平滑处理。

设定组合导航系统处在晃动环境下，仿真总时间为4000s，仿真条件设置如下：

1）舰船的初始位置为北纬35°、东经120°、初始航向角为45°。

2）受海浪的影响，横摇、纵摇、艏摇幅值为10°、5°、5°，周期为 9s、6s、6s； 垂荡、纵荡、横荡线速度幅值为0.02m、0.03m、0.1m，周期为7s、6s、8s。

3）惯导加速度计随机误差考虑1阶马尔可夫过程为1×10－5g；陀螺仪随机误差考虑随机常数为0.01（°）/h，白噪声为 0.01（°）/h，1 阶马尔可夫过程为 0.01（°）/h。

4）GPS经纬高位置误差为20m、20m、50m，东向、北向、天向速度误差为0.2m/s、0.2m/s、0.2m/s。

在此仿真条件下，Kalman滤波与固定区间平滑滤波的误差曲线对比如图2～图7所示。

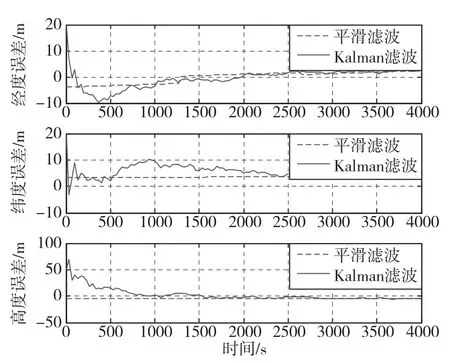
图2 位置估计误差曲线Fig.2 Curves of position estimation error

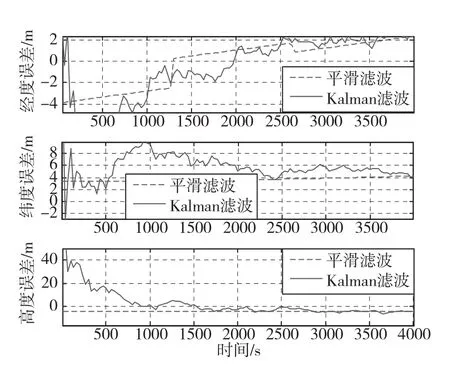
图3 位置估计误差局部放大图Fig.3 Curves of partial enlarged position estimation error

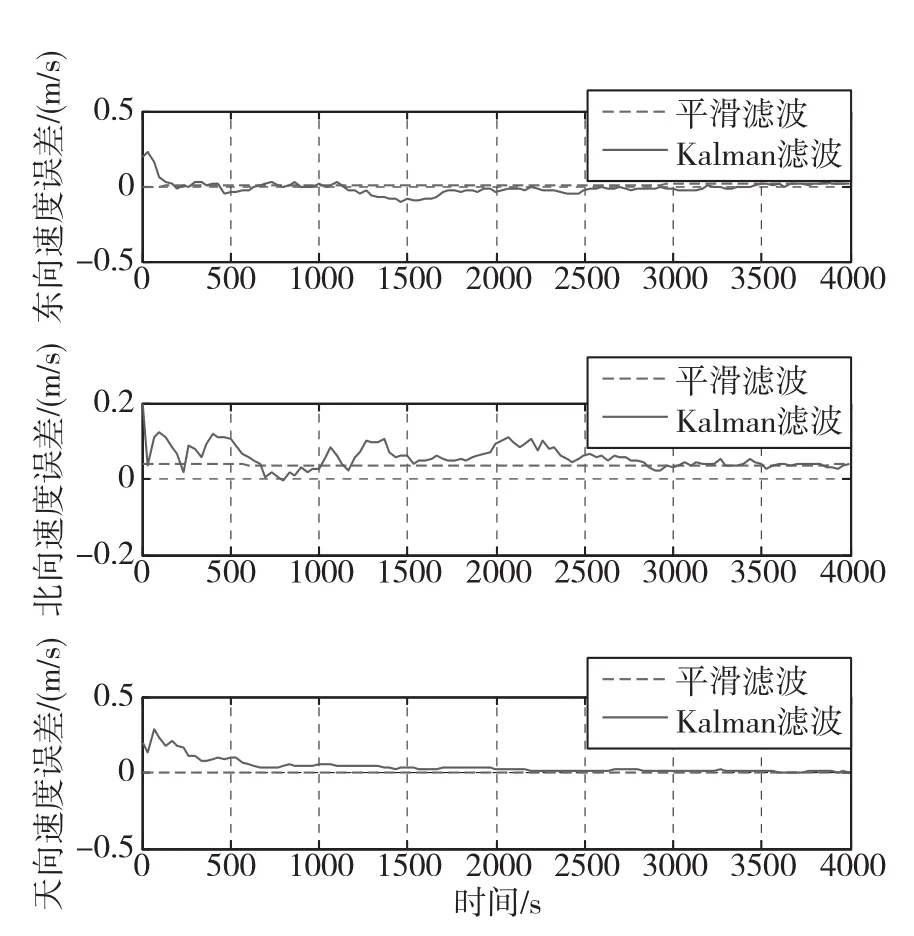
图4 速度估计误差曲线Fig.4 Curves of velocity estimation error

图5 速度估计误差局部放大图Fig.5 Curves of partial enlarged velocity estimation error

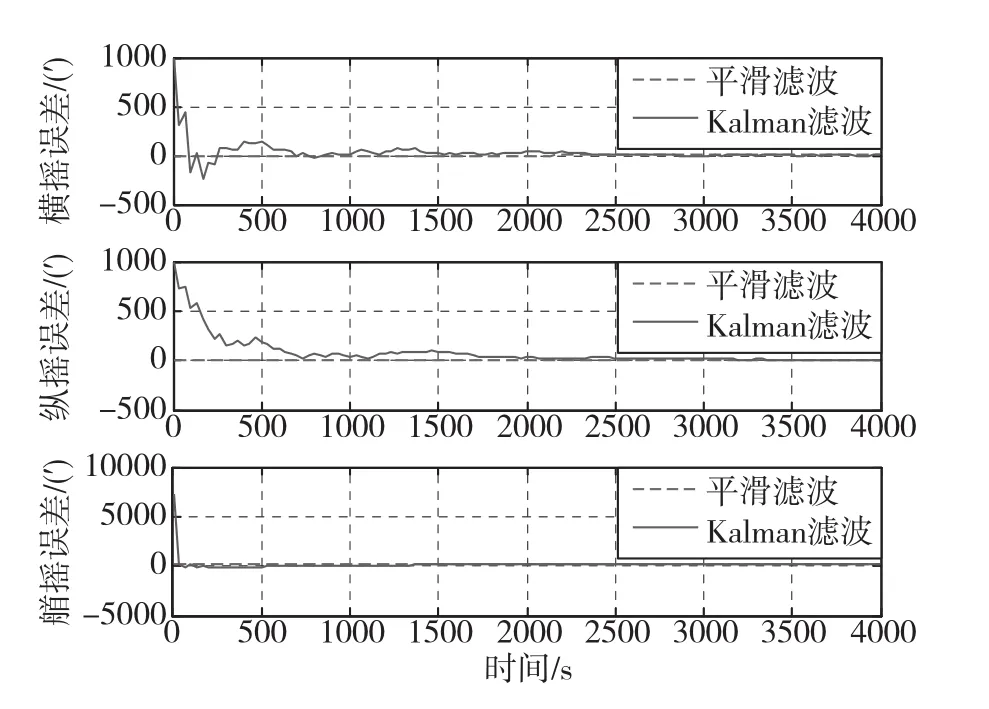
图6 姿态估计误差曲线Fig.6 Curves of attitude estimation error

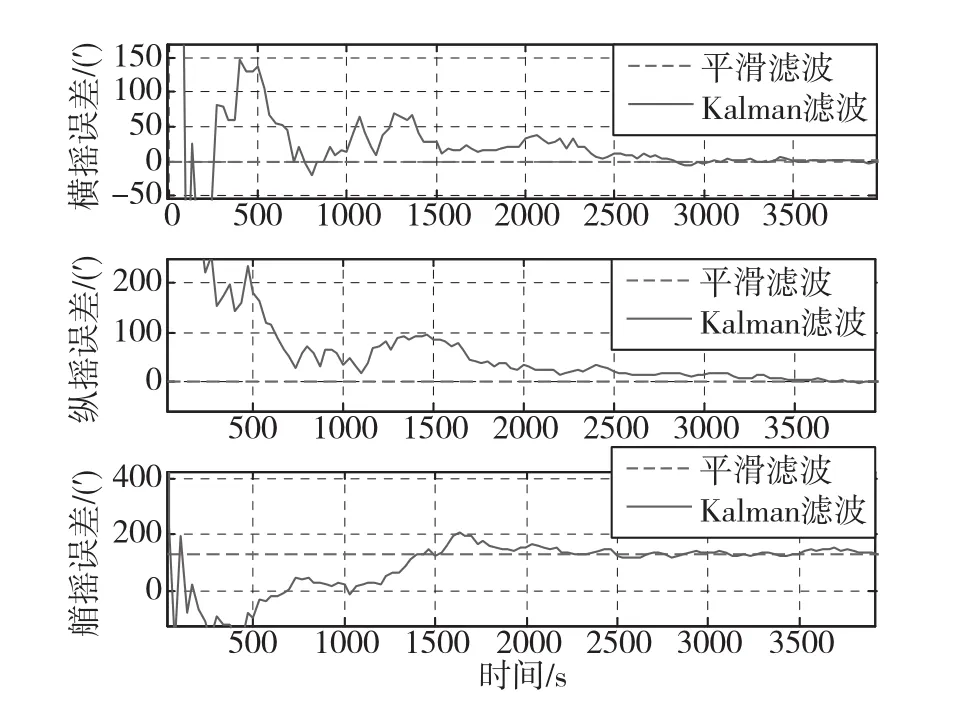
图7 姿态估计误差局部放大图Fig.7 Curves of partial enlarged attitude estimation error

由误差曲线图可以看出，固定区间最优平滑算法得到导航参数的估计误差值与Kalman滤波器相比较为平缓，误差更小。对上述结果做进一步量化分析，表1对比了2种滤波方式下各导航误差的均值与方差。当舰船处于晃动环境时，海风和波浪对组合导航精度产生了影响。因此，在不同的海况下，系统能达到的理想精度也不同。利用该方法可以考核各种海洋环境下导航系统的精度，并能够通过海上试验对导航数据进行事后评估，以满足不同的海上作业需求。

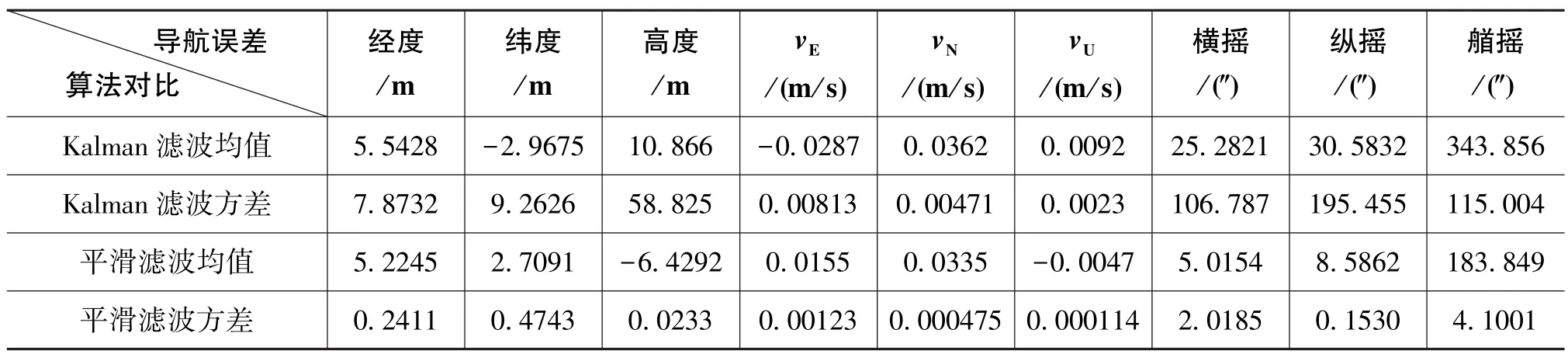
表1 导航信息误差对比表Table 1 Navigation error contrast between two methods

4 结论

本文研究了晃动环境下固定区间平滑算法及其在GPS/SINS组合导航系统事后评估中的应用，在算法研究的基础上，搭建了系统仿真平台，验证了算法性能，给出了相应的导航结果。与Kalman滤波算法相比，固定区间平滑滤波充分利用了观测时间间隔内的全部观测信息对导航数据进行事后分析，导航参数误差曲线收敛更快，变化也更为平缓。因此，该方法可以针对不同的海况以及不同的海上作业需求，有效地为组合导航系统精度提供检验标准，考核各种海洋环境下的导航系统精度。

[1]王珏，潘高峰，黄晓娟，等.船载GPS测姿系统数字滤波算法[J].中国惯性技术学报，2009，17（3）:284-287.WANG Jue，PAN Gao-feng，HUANG Xiao-juan，et al.Digital filtering algorithm in ship-based GPS attitude measurement system[J].Journal of Chinese Inertial Technology，2009，17 （3）:284-287.

[2]信冠杰，卞鸿巍，王战军，等.基于Q-R分解的平滑算法在惯导参数标定中应用[J].中国惯性技术学报，2010，18 （5）:633-638.XIN Guan-jie，BIAN Hong-wei，WANG Zhan-jun，et al.Application of smoothing algorithm based on Q-R decomposition in INS parameter calibration[J].Journal of Chinese Inertial Technology，2010，18 （5）:633-638.

[3]Bhatti U I，Ochieng W Y，Feng S.Performance of rate detector algorithms for an integrated GPS/INS system in the presence of slowly growing error[J].GPS Solutions，2012，16 （3）:293-301.

[4]宫晓琳，张蓉，房建成.固定区间平滑算法及其在组合导航系统中的应用[J].中国惯性技术学报，2012，20 （6）:687-693.GONG Xiao-lin，ZHANG Rong，FANG Jian-cheng.Fixed-interval smoother and its applications in integrated navigation system[J].Journal of Chinese Inertial Technology，2012，20 （6）:687-693.

[5]Yoon H，Sternberg D C，Cahoy K.Interpolation method for update with out-of-sequence measurements:the augmented fixed-lag smoother[J].Journal of Guidance，Control，and Dynamics，2016，39 （11）:2546-2553.

[6]袁涛，曲志刚，徐景硕，等.航母舰载机捷联惯导系统自主对准算法流程研究[J].弹箭与制导学报，2013，33 （2）:23-26.YUAN Tao，QU Zhi-gang，XU Jing-shuo，et al.Algorithm research on independent alignment of aircraft carrier's SINS[J].Journal of Projectiles，Rockets，Missiles and Guidance，2013，33 （2）:23-26.

[7]Chang L，Li J，Li K.Optimization-based alignment for strapdown inertial navigation system:comparison and extension [J]. IEEE Transactions on Aerospace and Electronic Systems，2016，52 （4）:1697-1713.

[8]赖际舟，柳敏，李志敏，等.基于有色噪声自回归建模的惯性/卫星交互多模型滤波导航算法[J].导航定位与授时，2015，2 （6）:19-24.

LAI Ji-zhou，LIU Min，LI Zhi-min，et al.Interacting multiple model filter algorithm of the inertial/GPS integrated system based on the colored noise regression modeling[J].Navigation Positioning and Timing，2015，2（6）:19-24.

[9]Weinert H L.Fixed interval smoothing for state space models[M].New York：Springer Science＆ Business Media，2001.

Research on Accuracy Post⁃evaluation Algorithm of the Integrated Navigation System in the Shaking Environment

CHEN Wei-na，ZENG Qing-hua，LIU Jian-ye，WANG Hui-zhe

（Navigation Research Center，Nanjing University of Aeronautics ＆ Astronautics，Nanjing 211106）

The ship rocks with the sea breeze，waves，currents and other factors，and thus cause serious interferences to the marine navigational system，reducing its accuracy.The fixed-interval optional smoothing algorithm uses all the observation information in the observation time interval to observe the minimum variance estimation of the state，which can implement post-evaluation of navigation accuracy.In this paper，based on the principle of the application of smoothing filter algorithm to SINS/GPS integrated navigation in the shaking environment，Kalman filter is used for integrated navigation，and related information is stored in time.Then，the fixed interval smoothing filtering algorithm is used in post-analysis.The method can be used to provide and access the accuracy evaluation for the navigation system of various marine environments because of different sea conditions and different sea operation requirements.

integrated navigation；Kalman filtering；fixed-interval；optional smoothing

U666.1

A

1674-5558（2017）01-01371

10.3969/j.issn.1674-5558.2017.06.002

2017-02-13

国家自然科学基金（编号：61533008，61328301）；中央高校基本科研业务费专项资金（编号：NS2015037）；南京航空航天大学博士学位论文创新与创优基金（编号：BCXJ13-05）

陈维娜，女，博士，研究方向为惯性技术、组合导航的研究。