基于波束空间二维谱峰搜索的无人机控制算法
2017-12-20陆兴华
陆兴华
(广东工业大学华立学院,广东 广州 511325)
基于波束空间二维谱峰搜索的无人机控制算法
陆兴华
(广东工业大学华立学院,广东 广州 511325)
无人机作大范围机动航行时,由于陀螺仪的交连误差导致飞行稳定性不好,需要进行稳定性控制。传统的控制算法采用扇面波束空间约束加权误差修正算法,不能有效满足姿态大范围变化的控制需求。因此,提出一种基于波束空间二维谱峰搜索的无人机飞行鲁棒性控制算法。描述了无人机作大范围机动航行的控制约束参量模型和纵向运动数学模型,采用相干分布源采集飞行姿态数据,根据姿态数据解出无人机的动力系数、传递函数和频域特性等控制约束参量;采用波束空间二维谱峰搜索方法进行陀螺仪的交连误差补偿和自适应控制,较好地处理无人机不确定动态运动系统的控制问题。仿真结果表明,采用该算法进行无人机飞行控制,较好地削弱了陀螺仪的交连误差对飞行姿态的速度和位置等参量带来的波动,飞行姿态解算的误差结果较小,控制品质较高。
波束空;二维谱峰搜索;无人机;控制
0 引 言
随着飞行器设计和飞行器制造技术的不断发展,飞行器的种类不断扩大,设计工艺逐渐完善,用途越来越广泛。无人机是飞行器的重要分支,是利用无线电遥控设备和自备的程序控制装置操纵的不载人飞机。无人机具有隐蔽性强、机动性好、危险系数低和成本低等优点,广泛应用于军事领域和民用特种领域,在作为侦察机和靶机、航拍、农业、植保、快递运输、灾难救援、影视拍摄等方面都展示了较好的应用价值。无人机的大范围机动性能有效拓展无人机的应用范围。在无人机作大范围机动航行时,由于陀螺仪的交连误差导致飞行稳定性不好,需要进行稳定性控制。因此,研究无人机的飞行稳定性控制算法是进行无人机设计的核心,相关的算法研究受到了极大重视。
无人机的飞行稳定性控制是进行飞行惯导设计和飞行动力学设计的关键技术。飞行控制的核心是飞行的鲁棒性及稳定性。通过飞行姿态数据的实时采集和传输,与飞行惯导系统进行信息交互和陀螺仪控制,执行飞行控制指令。传统方法中,对无人机的飞行控制算法设计主要有模糊神经网络控制算法、PID控制算法、滑膜控制算法、稳态积分控制算法等[1-3]。通过构建相应的控制器,进行姿态误差修正和扰动补偿,实现了飞行稳定性控制,提高了飞行控制品质,取得了一定的研究成果。例如,文献[4]提出一种基于单自由度速率跟踪和惯导失衡补偿的无人机飞行控制算法,求得速率陀螺仪的跃阶响应,通过转动惯量的动量矩特征分析,构建稳态方程实现飞行稳定性控制。该算法提高了控制精度,但计算开销较大,对飞行状态控制的实时性不好;文献[5]提出一种基于能量反演参数自整定修正的飞行姿态控制算法,实现了对大回环飞行下的无人机控制。由于对姿态参量采用模糊PID进行自适应修正,该算法提高了飞行的抗扰动性,但需要大量的飞行姿态先验数据和规则作为引导,在先验信息缺乏时,控制效果不好;文献[6]对无人机飞行控制采用扇面波束空间约束加权误差修正算法,不能有效满足姿态大范围变化的控制需求。
针对上述问题,文中提出一种基于波束空间二维谱峰搜索的无人机飞行鲁棒性控制算法。描述了无人机作大范围机动航行的控制约束参量模型和纵向运动数学模型,实现了控制算法的改进设计,并通过仿真实验对其有效性进行验证。
1 无人机控制约束参量模型和纵向运动数学模型
1.1 无人机作大范围机动航行的无人机控制约束参量模型
为了实现对无人机作大范围机动航行时的飞行稳定性控制,首先需要构建无人机控制约束参量模型和飞行运动的动力学数学模型。建立无人机的纵向运动模型,在速度坐标系、体坐标系、弹道坐标系和地面坐标系中进行无人机的控制参量约束分析。无人机飞行过程中,除初始非操纵段外,其速度变化一般很小[7]。飞行的速度变化过程可以表示为一个连续渐进的状态变量,对飞行姿态的渐进变量求导,得到无人机飞行轨迹跟踪控制系统满足如下非光滑时变函数:
(1)
根据线性化小扰动的优化条件,当x(t)=[x1(t),x2(t),…,xt(t)]T表示的扰动向量误差矩阵收敛时,在弹道某些特征点附近,设无人机在相对惯性空间内的相干分布源模型为:
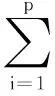
(2)
其中

(3)
无人机在作大范围空间机动航行时,控制系统的参数测量矢量为s(t)=[s1(t),s2(t),…,sq(t)]T,扰动矢量为n(t),两者是相互独立的零均值随机矢量。姿态参量和扰动参量之间的二阶矩分别为:
(4)
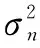
在连续时滞下通过多传感器融合跟踪进行飞行姿态数据的线性滤波和拟合,构建一个线性时变系统对无人机的飞行轨迹进行动力学平衡拟合,拟合过程用微分方程描述为:
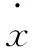
(5)
通过上述系统状态分析和设计,用累加时变方法将稳定性解推广到整个飞行的水平平面和纵向平面中,分析无人机飞行的动静力特性。当无人机受到扰动作用时,气流扰动的量化噪声表示为:
mi(k)=zi(k)+qi(k)=
Hi(k)x(k)+ui(k)+qi(k):=
Hi(k)x(k)+vi(k)
(6)
其中,无人机在受到不确定气流扰动下的量化跟踪误差qi(k)的方差满足:


(7)
考虑存在不确定对流扰动下无人机作大范围机动航行的横滚侧向应力[8-10],对陀螺仪产生的交连误差进行自适应误差修正,得到的无人机教练误差补偿后的控制输出状态方程为:
(8)
根据上述分析,实现对无人机作大范围机动航行的无人机控制约束参量模型构建,从而设计被控对象和控制目标函数,进行无人机飞行控制优化。
1.2 无人机纵向运动数学模型及被控对象描述
在上述进行了控制约束参量分析的基础上,构建无人机纵向运动数学模型。无人机的运动方程主要包括质心运动方程、质心动力学方程。在无人机作大范围空间机动航行的前提下[11],构建无人机的线性扰动方程组,采用姿态传感器得到观测的无人机飞行姿态数据矢量z(t)的协方差矩阵可以表示为:
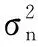
(9)
其中,B=[b1(θ1),b2(θ1),…,bq(θq)]T;无人机飞行姿态的中心波达方向为θi和扩展角σi,作用在飞行惯导陀螺仪上的外力矩协方差矩阵的奇异值分解为:
(10)
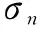
在干扰力矩的作用下,使用单自由度的系数冻结法,在弹道某些特征点附近[12],给出无人机的常系数线性微分方程组:
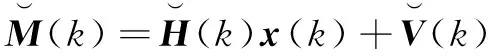
(11)
其中
(12)

综合上述分析,将无人机作大范围机动航行的飞行姿态动力学分析问题转化为如下极小化问题的解:
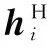
(13)
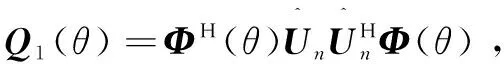
2 无人机鲁棒性控制算法改进的实现
2.1 问题的提出及控制目标函数构建
在上述无人机作大范围机动航行的控制约束参量模型和运动数学模型构建的基础上,进行控制算法改进设计。无人机作大范围机动航行时,由于陀螺仪的交连误差导致飞行稳定性不好,需要进行稳定性控制。传统的控制算法采用扇面波束空间约束加权误差修正算法,不能有效满足姿态大范围变化的控制需求。为了克服传统方法的弊端,提出一种基于波束空间二维谱峰搜索的无人机飞行鲁棒性控制算法。根据上述构建的无人机纵向运动数学模型,采用相干分布源采集飞行姿态数据,在一定飞行高度下满足wij=αij。融合中心相对应于系统原点满足有限时间稳定性,采用二次性能指标[13],在最优控制律引导下,无人机的纵向运动控制满足有限时间收敛性,表示为:
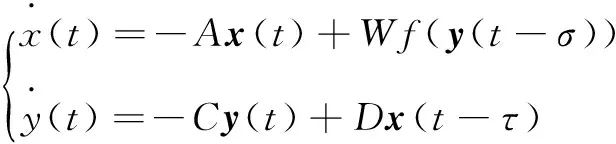
(14)
并有:
x(t)=[x1(t),x2(t),…,xn(t)]T
(15)
y(t)=[y1(t),y2(t),…,yn(t)]T
(16)
f(y(t))=[f1(y1(t)),f2(y2(t)),…,
fn(yn(t))]T
(17)
f(y(t))=g(y(t)+p*)-g(p*)
(18)
根据姿态数据解出无人机的动力系数、传递函数和频域特性等控制约束参量,在控制向量波束空间内,无人机飞行姿态阵列数据矩阵为y(t)=TH(n)x(t),其协方差矩阵Ryy的特征值表示为λi,vi(i=1,2,…,l),l为单自由度陀螺仪作用下的空间波束域的波束个数。无人机的环轴在正弦外力矩作用下特征值大小顺序为:λ1,…,λd,…,λl。综合考虑特征值的大小对控制稳定性产生的影响[14],得到飞行扰动子空间为:
(19)
其中,L(λd+1vd+1,λd+2vd+2,…,λlvl)表示干扰力矩的张成子空间。
(20)
采用波束域噪声子空间估计进行稳定状态求解,若姿态参量采集的阵元数目为M,则波束转换矩阵T(n)(N×L)可以表示为:
T(n)=w[v(1),v(2),…,v(L)]
(21)
其中
v(i)=
[1,ej2πdsin(θ(i))/λ,ej2π2dsin(θ(i))/λ,…,ej2π(M-1)dsin(θ(i))/λ]T
(22)
采用自适应谱峰加权搜索进行飞行控制,采用波束矩阵的加权向量矩阵控制波束主瓣宽度以及旁瓣高度,降低无人机作大范围机动航行时对稳态误差的影响。此时飞行控制波束空间的转换过程可以表示为:y(t)=TH(n)x(t),经过转换后得到控制目标函数为:
RB(n)=E{y(t)yH(t)}=
TH(n)E{x(t)xH(t)}T(n)=
TH(n)RT(n)
(23)
在不确定飞行外力矩扰动下,无人机出现抖振等振荡特性,采用扇面波束空间约束进行振荡抑制,相关矩阵可以表示为:
(24)
其中,B=[b1,b2,…,bq],其特征分解式为:
(25)
经过上述分析,实现了对无人机作大范围机动航行时的控制目标函数构建,以此为基础,进行控制算法优化设计。
2.2 基于波束空间二维谱峰搜索的控制算法实现
采用波束空间二维谱峰搜索方法进行陀螺仪的交连误差补偿和自适应控制,较好地处理无人机不确定动态运动系统的控制问题。
在波束域内,无人机飞行航向陀螺仪接收到的姿态数据的相关矩阵为:
RB(n)=E{y(t)yH(t)}=TH(n)E{x(t)xH(t)}
T(n)=TH(n)RT(n)
(26)
其中,T(n)为波束转换矩阵。
无人机受到不确定气流扰动下陀螺仪的输入瞬态响应特征分解为:
(27)
为了实现无人机流体动力平衡,利用波束域方向矢量biB的一阶近似biB(θi,ζi),得到第i个控制波束域方向矢量biB(θi)=THbi(θi),得到无人机稳定性控制的极小化问题的解:
(28)
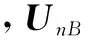
根据求解有约束条件下的拉格朗日极值问题,波束空间二维谱峰搜索控制的拉格朗日代价函数为:
L(θ,ζ)=ζTQ(θ)ζ+2β(1-ζTw)
(29)
其中,β为拉格朗日系数。
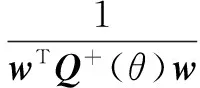
(30)
由此实现对陀螺仪的交连误差补偿。根据空间谱的形式,用间隔扫描的办法得出谱峰值对应的参数,得到无人机鲁棒性自适应控制的空间谱的谱峰位置:
f(θ)=wTQ+(θ)w
(31)
通过上述分析,采用波束空间二维谱峰搜索方法进行陀螺仪的交连误差补偿和自适应控制,实现控制算法改进,较好地处理无人机不确定动态运动系统的控制问题。
3 仿真实验与结果分析
为了测试文中算法的应用性能,在Matlab7.0数值仿真平台上对其进行仿真实验。实验的硬件环境为:Tektronix TX3 True RMS MultiMeter;Agilent 33220A函数信号发生器;INSTEK PST3202可编程电源;Agilent混合示波器。无人机飞行姿态数据采样率大于等于200 kHz,D/A分辨率为12位(至少),输入无人机飞行姿态数据采样阵列源的扩展角度分别为Δ1=50,Δ2=80,飞行位姿变换的方位分别为-5°和10°,飞行扰动干扰的信噪比为2 dB,主旁瓣高度比为30 dB。根据上述仿真环境和参数设定,首先给出在阵元域内的飞行姿态信息采样的波束图,如图1所示。
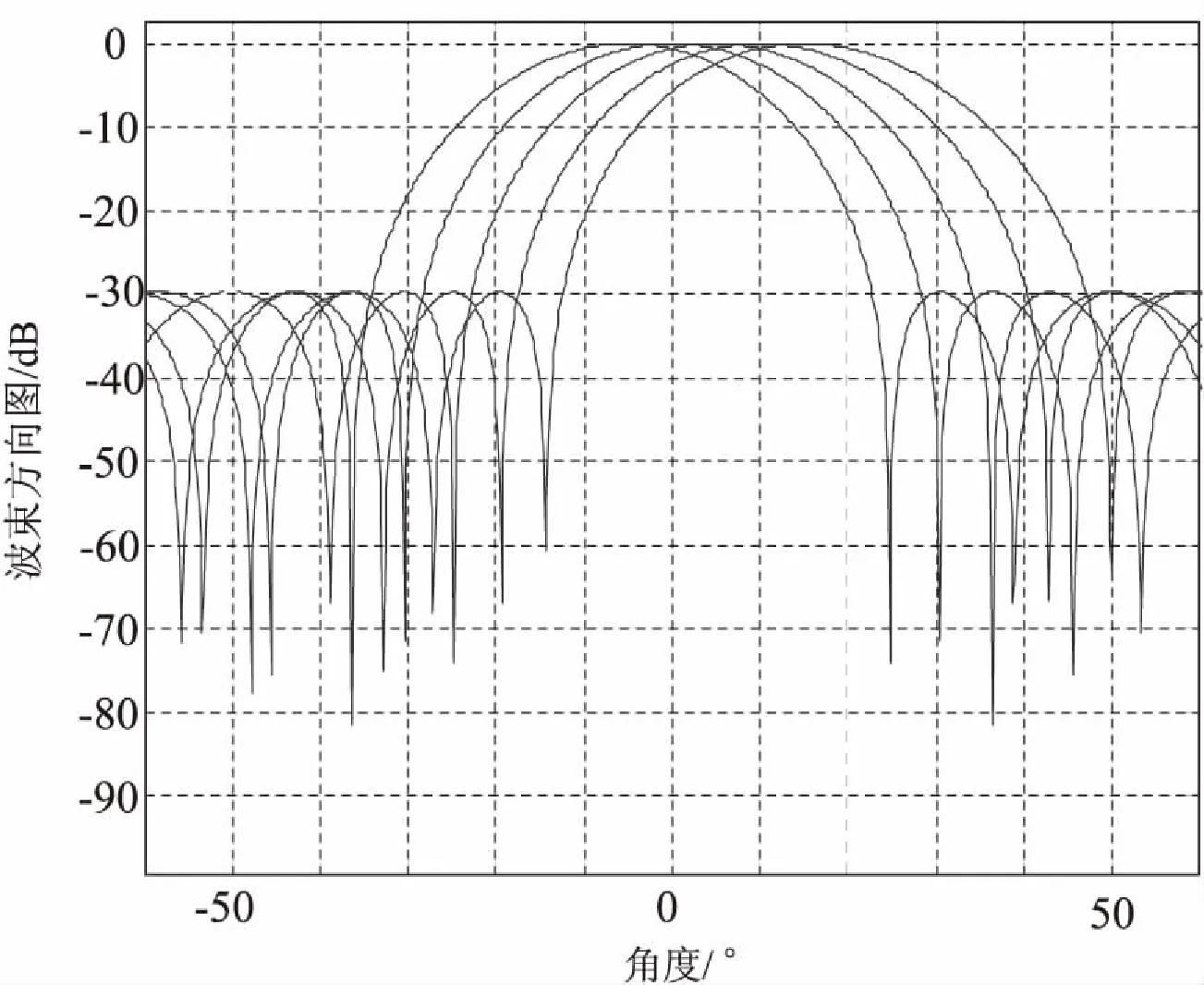
图1 阵元域内的飞行姿态信息采样波束图
采用相干分布源采集飞行姿态数据,根据姿态数据解出无人机的动力系数、传递函数和频域特性等控制约束参量,采用波束空间二维谱峰搜索方法进行陀螺仪的交连误差补偿和自适应控制。采用文中方法和传统的阵元域一阶近似法得到的飞行控制空间增益如图2所示。
由实验结果可以看出,采用文中方法进行波束域空间的二维谱峰搜索,波束域的一阶近似法比阵元域方法在谱峰尖锐度上有所提高,从而提高了控制精度。为了定量对比在实现无人机飞行的速度控制和位置控制中的性能,采用文中算法和传统的PID控制方法,得到无人机的速度和位置的控制输出与预设目标状态的跟踪控制结果,如图3所示。
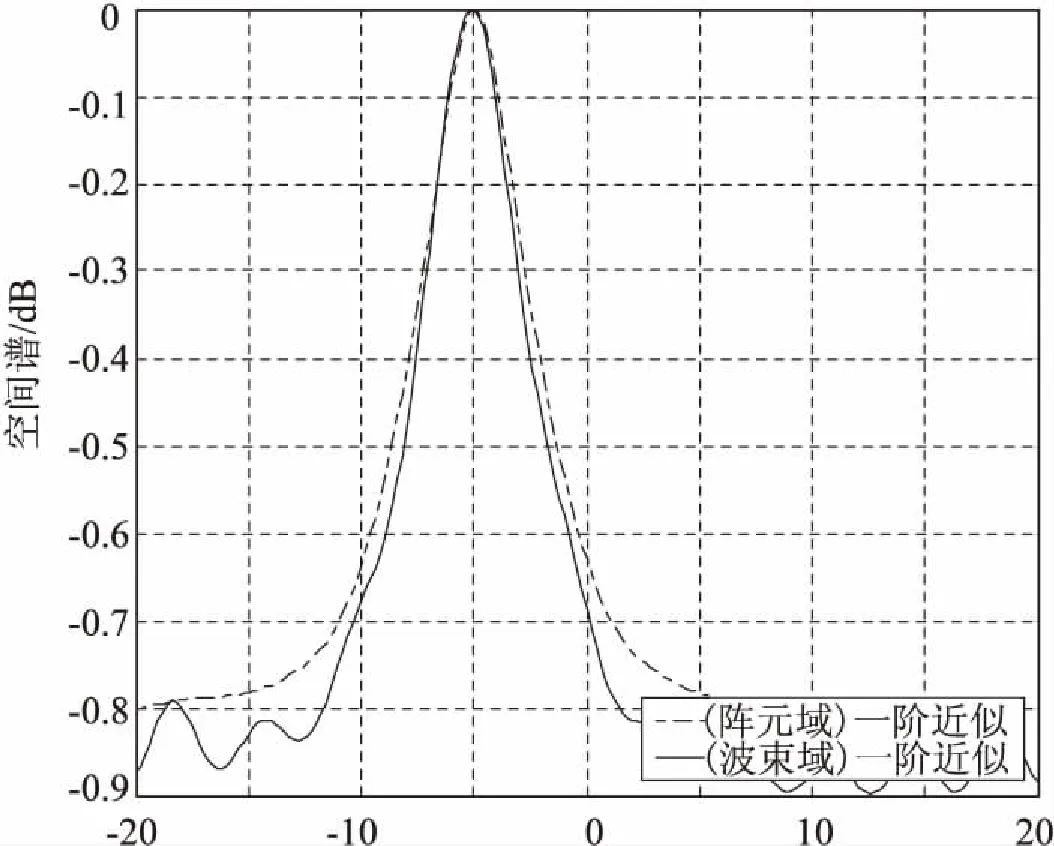
图2 谱峰搜索估计结果
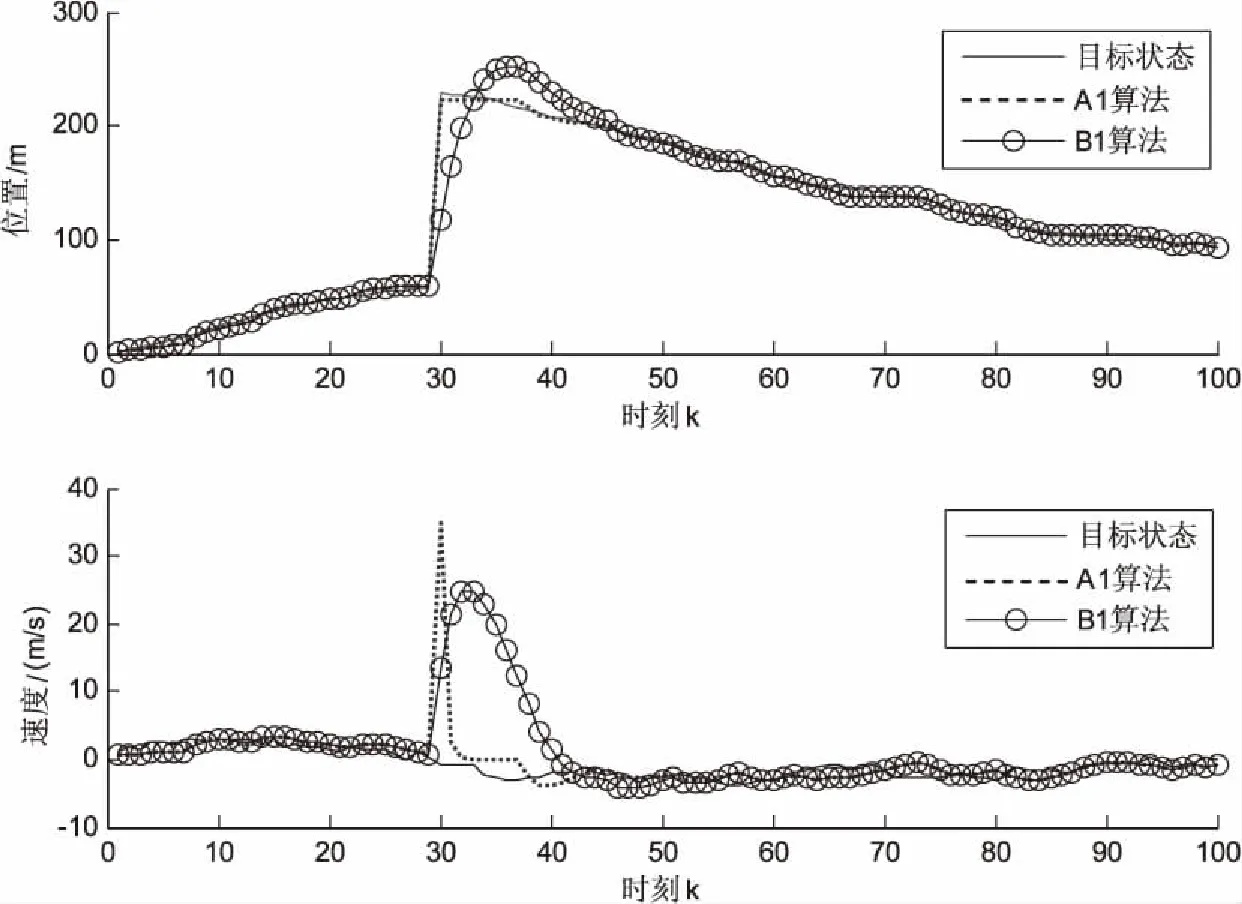
图3 两种算法对无人机飞行控制的参量输出评估对比
对结果进行整理分析,得出两种算法对无人机控制的位置和速度参量的误差结果,见表1。
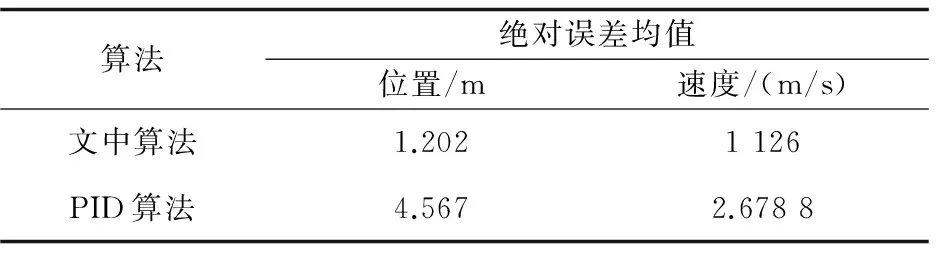
表1 两种算法的绝对误差均值
分析图3和表1的实验结果可知,采用文中算法进行无人机飞行控制,对飞行方位和速度等姿态参量的控制精度较高,误差较低,较好地削弱了陀螺仪的交连误差对飞行姿态的速度和位置等参量带来的波动,飞行姿态解算的误差结果较小,提高了控制品质,展示了优越性能。
4 结束语
文中提出一种基于波束空间二维谱峰搜索的无人机飞行鲁棒性控制算法。首先描述了无人机作大范围机动航行的控制约束参量模型和纵向运动数学模型,采用相干分布源采集飞行姿态数据,根据姿态数据解出无人机的动力系数、传递函数和频域特性等控制约束参量,采用波束空间二维谱峰搜索方法进行陀螺仪的交连误差补偿和自适应控制,较好地处理无人机不确定动态运动系统的控制问题。实验结果表明,采用该算法进行无人机飞行控制,对飞行姿态的速度和位置等参量控制的精度较高,误差较低,控制品质较高,性能优于传统方法。
[1] 陆兴华,陈平华.基于定量递归联合熵特征重构的缓冲区流量预测算法[J].计算机科学,2015,42(4):68-71.
[2] Lee W,Bang H,Leeghim H.Cooperative localization between small UAVs using a combination of heterogeneous sensors[J].Aerospace Science and Technology,2013,27(1):105-111.
[3] 葛立志.基于全弹道控制分析的水下航行器攻击模型视景仿真[J].舰船电子工程,2015,35(3):137-141.
[4] 王 勋,张代兵,沈林成.一种基于虚拟力的无人机路径跟踪控制方法[J].机器人,2016,38(3):329-336.
[5] Brox T, Malik J. Large displacement optical flow:descriptor matching in variational motion estimation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,33(3):500-513.
[6] Evangelio R H,Patzold M,Keller I.Adaptively splitted GMM with feedback improvement for the task of background subtraction[J].IEEE Transactions on Information Forensics and Security,2014,9(5):863-874.
[7] 何大阔,高飞雪,杨 乐,等.一类未知MIMO非线性离散系统的改进自适应准滑模解耦控制[J].控制与决策,2016,31(5):783-789.
[8] 黄国顺,文 翰.基于边界域和知识粒度的粗糙集不确定性度量[J].控制与决策,2016,31(6):983-989.
[9] 窦慧晶,王千龙,张 雪.基于小波阈值去噪和共轭模糊函数的时频差联合估计算法[J].电子与信息学报,2016,38(5):1123-1128.
[10] 李 旭,彭 欢,王春辉.星载激光测距仪APD最佳雪崩增益控制技术研究[J].红外与激光工程,2016,45(5):69-74.
[11] Eldemerdash Y A,Marey M,Dobre O A,et al.Fourth-order statistics for blind classification of spatial multiplexing and alamouti space-time block code signals[J].IEEE Transactions on Communications,2013,61(6):2420-2431.
[12] Lin Y P,Vaidyanathan P P.Theory and design of two-dimensional filter bank:a review[J].Multidimensional System & Signal Processing,1996,7(3-4):263-330.
[13] Suzuki T,Kudo H.Two-dimensional non-separable block-lifting structure and its application to M-channel perfect reconstruction filter banks for lossy-to-lossless image coding[J].IEEE Transactions on Image Processing,2015,24(12):4943-4951.
[14] 明平松,刘建昌.随机多智能体系统一致稳定性分析[J].控制与决策,2016,31(3):385-393.
UnmannedAerialVehicleControlAlgorithmBasedonTwoDimensionalSpectrumPeakSearchingforBeamSpace
LU Xing-hua
(Huali College Guangdong University of Technology,Guangzhou 511325,China)
Due to the error of the gyroscope,the stability of the aircraft is not good,and the stability control is needed when the Unmanned Aerial Vehicle (UAV) is maneuvering in a large scale.The traditional control algorithm uses constrained weighted error correction algorithm of fan beam space and cannot effectively meet the attitude changes in the scope of the control demand.Therefore,a robust control algorithm for UAV flight based on two-dimensional spectrum peak searching is proposed.It describes the control constraint parameter model and mathematical model of longitudinal motion when UAV navigating in a wide range,and uses coherent distributed source for acquisition of flight attitude data by which the control constraints parameters like dynamic coefficients,transfer function and frequency characteristics for UAV are solved,and applies beam space 2-D spectral peak searching method for even error compensation and adaptive control of gyroscope,better processing of UAV uncertain problem of dynamic system control.The simulation results show that the proposed algorithm is used to carry out UAV flight control,which can effectively reduce the error of the gyro and the flight chattering,and the result of the error is small and the control quality is high.
beam space;two-dimensional spectral peak search;unmanned aerial vehicle;control
TP273
A
1673-629X(2017)12-0052-05
10.3969/j.issn.1673-629X.2017.12.012
2016-11-25
2017-03-28 < class="emphasis_bold">网络出版时间
时间:2017-08-01
2015年广东省教育重点平台及科研项目青年创新人才类项目(自然科学类)(2015KQNCX218);2012广东省质量工程项目(粤教高函[2012]204号)
陆兴华(1981-),男,硕士,讲师,研究方向为计算机控制算法、人工智能。
http://kns.cnki.net/kcms/detail/61.1450.TP.20170801.1552.046.html
