应力条件下页岩二维数字岩心的改进研究

李江涛，汪志明*，魏建光，赵岩龙，闵健

1 中国石油大学石油工程教育部重点实验室，北京 102249 2 中国石油大学(北京)油气资源与探测国家重点实验室，北京 102249 3 东北石油大学石油工程学院，大庆 163000

应力条件下页岩二维数字岩心的改进研究

李江涛1,2，汪志明1,2*，魏建光3，赵岩龙1,2，闵健1,2

1 中国石油大学石油工程教育部重点实验室，北京 102249 2 中国石油大学(北京)油气资源与探测国家重点实验室，北京 102249 3 东北石油大学石油工程学院，大庆 163000

目前常用的数字岩心数值重构方法都是基于常压下得到的扫描电镜(SEM)图片或CT扫描结果，导致数字岩心孔隙结构与实际地层有偏差，不利于分析页岩的孔隙特点及模拟页岩气在数字岩心中的流动。本文基于二维数字岩心和岩石弹性力学方程建立了应力条件下页岩数字岩心矿物骨架和有机质的位移计算模型，对数字岩心孔隙结构进行了修正，得到了应力条件下的页岩数字岩心。利用模型模拟了不同应力条件下岩心的孔隙结构变化规律，结果表明：有机质中的纳米孔隙对应力更加敏感，随应力变化的程度更大。对于比较细长的孔隙，受到应力作用后沿短轴方向的位移要比沿长轴方向的要大，会导致一些细长孔隙闭合或形成几个孤立的孔隙。孔隙压力对有机质纳米孔影响最大，会影响页岩气在有机质纳米孔中的流动。数字岩心的修正为进一步利用格子Boltzmann方法研究页岩气的微观渗流规律提供了更准确的流动通道模型。

页岩；数字岩心；应力；孔隙度

0 引言

页岩储层孔隙结构复杂，孔隙尺度变化大，既有纳米级的有机质孔也有微米级的矿物骨架孔，还存在有天然微裂缝。页岩的孔隙结构及尺寸分布对页岩气渗流规律有很大的影响，页岩气在不同的孔隙中可能存在扩散、吸附解吸、滑脱和达西流动等不同的渗流类型，页岩的孔隙结构和渗透率存在很强的压敏效应[1-3]，因此得到符合实际地层情况的页岩孔隙结构对研究页岩气的渗流规律有重要意义。数字岩心技术具有孔隙结构直观、便于分析及参数可灵活调整等优点，近年来，基于数字岩心技术的页岩气微观渗流规律研究受到越来越多学者的关注[4-7]。

数字岩心重构方法主要有2类。一类是通过物理手段直接测量并数值化，如CT扫描成像法[8-9]，这类方法能得到测试岩样的真实孔隙结构，但不能够重复构建，不能预测地层其他位置的孔隙结构，而且这种方法精度和测量范围不能兼顾，如果对精度要求比较高，则测量范围会很窄，不能代表大范围的孔隙分布特征。另一类是利用扫描电镜图片，统计岩样的参数，如孔隙度、孔隙尺寸分布等，结合不同的数学统计预测方法对岩样进行重构，得到符合岩样参数统计规律的数字岩心。这类方法统计参数的取得方式比较灵活，成本比较低，既可以满足精度要求，又可以大范围地进行扫描。数学统计预测方法有随机生长法、高斯模拟法[10-11]、模拟退火法[12-13]、多点统计法[14-15]、马尔科夫链-蒙特卡洛方法(Markov chain Monte Carlo method, MCMC)[16-17]等，可以针对不同的岩石类型选择不同的方法。在重构过程中，可以人为地灵活调整参数，分析不同因素的影响，因此这类方法得到越来越多的应用。

由于实验条件的限制，目前CT扫描结果和扫描电镜图片都是在常温常压下得到的，而储层实际受到地应力和孔隙压力的作用，因此用常压下得到的数字岩心来模拟页岩气的渗流与实际情况存在误差。而且在开采过程中，随着孔隙压力的降低，页岩受到的有效应力也在不断变化，页岩孔隙是一个动态的变化过程，因此基于数字岩心对页岩气渗流进行研究时，需要对岩心进行实时的应力应变修正。李荣强等[18]将均质的人造岩心施加围压，然后放入CT扫描仪中进行岩心压敏效应实验，得到围压升高和降低过程中的孔隙半径分布曲线、形状因子概率曲线、孔喉连通性的变化规律。这种方法需要在每个压力点进行CT扫描，岩心重构和分析过程比较繁琐，成本较高。鞠杨等[19]基于砂岩孔隙结构CT图像，利用ABAQUS软件中的有限元模型模拟了砂岩的三轴压缩的非线性变形，并利用格子玻尔兹曼方法(Lattice Boltzmann Method, LBM)分析了应力作用下孔隙结构变形对甲烷渗流的影响。相比于李荣强的研究，这种数字岩心加有限元模拟的方法节省了实验时间，可以模拟更多因素对岩石应力敏感的影响。但在实际模拟长时间的流体流动时，每模拟一步，就需要先用ABAQUS模拟岩样的变形，再用LBM模拟流体流动，这种方法也比较繁琐。因此需要建立基于数字岩心的岩石应力应变模型，可以方便地与LBM耦合模拟页岩气的流动。

为了研究应力条件下页岩数字岩心孔隙结构的变化，本文先利用MCMC方法建立了包含页岩矿物组分和有机质组分的二维数字岩心，再基于平面应力模型通过有限差分方法建立了数字岩心矿物骨架和有机质的位移计算模型，模拟了应力条件下矿物骨架微米孔和有机质纳米孔的变化规律，为正确研究页岩气在地层条件下的渗流规律提供了基础。

图1 页岩岩心扫描电镜图片Fig. 1 The SEM image of shale core

1 二维MCMC方法重构页岩数字岩心

MCMC法重构图像的主要思路是先利用阈值分割将扫描电镜图片二值化，0代表孔隙，1代表固体，再根据蒙特卡洛思想通过统计不同邻域的状态计算转移概率，再根据马尔可夫链思想利用已确定像素的状态和转移概率确定未知像素的状态[16-17,20]。

本文对四川盆地龙马溪组的页岩岩心进行了电镜扫描，由于矿物骨架孔隙主要为微米孔，而有机质孔隙主要为纳米孔，孔隙尺寸量级不一样，在相同分辨率条件下有机质的孔隙可能会显示不出来，因此对页岩矿物骨架和有机质分别进行扫描，得到了页岩矿物骨架和有机质的扫描图片，如图1所示，然后分别进行了数字岩心重构，如图2所示。由于矿物和有机质的单个像素代表的长度不同，需要将矿物数字岩心图片进行修正，然后将矿物骨架和有机质的数字岩心合并在一起得到含有有机质的页岩数字岩心，如图3所示。

图2 页岩重构数字岩心Fig. 2 The reconstructed digital core of shale

图3 含有有机质的页岩数字岩心Fig. 3 The shale digital core contain organic matter

由于模拟图3的二维数字岩心计算量太大，从中抽取出一部分进行模拟，如图4所示。通过统计施加应力前矿物骨架孔和有机质孔隙所占的像素比例[21]，得到该图片范围内的矿物骨架孔隙度为6.02%，有机质孔隙度为7.72%，总的孔隙度为7.01%。数字岩心在地层中受到地应力和孔隙压力的作用，受力示意图如图4所示，数字岩心的下边界和右边界采用固定边界。

2 二维数字岩心位移计算模型

二维数字岩心受到的应力符合平面应力条件，不考虑垂直平面的应力和应变，所受应力为x方向和y方向的压应力。由于岩心从地层取到地面是应力减小的过程，所以岩心并没有产生更多的破坏，可以认为数字岩心受到地应力作用后的应变是线性应变。根据广义Hooke定律，应力与应变关系为：

图4 数字岩心受力示意图Fig. 4 The stress schematic diagram of digital core

应变与位移的关系为：

联立式(1)-(6)，得到位移和应力的关系式：

平面上每个像素受到的应力是平衡的，不考虑面应力，可得到平衡方程为：

岩心在地层中不仅受到地应力的作用，孔隙中还存在孔隙压力，对岩石的应变也有影响。岩样所受到的地应力的边界条件为：

联立式(7)-(11)，可得到以位移为未知量的微分方程：

边界条件为：

利用有限差分方法，可得到式(12)和式(13)的有限差分格式：

其中，E为杨氏模量，MPa；λ为泊松比；u为各像素点沿x方向的位移，m；v为各像素点沿y方向的位移，m；Δx和Δy为单个像素点代表的长度，m；m和k分别表示矿物骨架和有机质，在矿物骨架和有机质的区域分别采用各自的弹性模量和泊松比。

矿物骨架和有机质的界面满足应力相等和位移连续的边界条件。以图4矿物骨架和有机质的上边界为例。对边界处位于有机质内部的像素点，受到矿物骨架对有机质在x方向的应力， 因此x方向采用应力边界条件，y方向采用平衡方程，边界条件如式(16)所示：

对边界处位于矿物骨架内部的像素点，受到有机质对矿物骨架在x方向的应力，因此x方向采用应力边界条件，y方向采用平衡方程，边界条件如式(17)所示：

同理可得矿物骨架和有机质在其它3个方向界面的边界条件。

对于孔隙壁面，也采用应力边界条件，边界应力值为孔隙压力，但由于孔隙是不规则的，在模拟过程中需要判断孔隙壁面的形状，建立相应的边界条件。如图5所示，一个像素点的应力边界条件需要判断其上、下、左、右4个点的状态，当待求像素周围4个点都为孔隙时，认为待求像素点为也为孔隙，位移设为0。待求像素周围4个点的状态有15种，需要建立15种孔隙的边界条件，在模拟时，需要判断孔隙边界，选择对应的边界条件。

联立式(14)和式(15)及矿物骨架和有机质的边界条件及孔隙壁面的边界条件，可求得应力条件下页岩矿物骨架和有机质各像素点的位移，从而可得到应力条件下孔隙的变化规律。

3 模型验证

Bernabe等人[22]通过理论推导得到了平面有椭圆孔隙的长、短半轴随孔压和围压的变化关系式：

式中：下标c为围压，下标p为孔压，a为椭圆孔长半轴，b为椭圆孔短半轴，G为剪切模量，MPa，。求解式(18)可得到平面存在椭圆孔隙条件下各像素点随应力的位移和应力条件下孔隙的变化规律。图6为围压25 MPa，孔压5 MPa 条件下平面存在椭圆孔隙的各像素点沿短轴方向和沿长轴方向的位移云图，颜色越红表示位移越大，可以看出在x方向和y方向围压相同条件下，像素点沿短轴方向的位移比沿长轴方向的位移大。在不同围压和孔压条件下的模拟结果与理论计算结果如图7-8所示。从图中可以看出模拟的椭圆孔隙长、短半轴随围压和孔压的变化与理论公式非常接近，误差最高为0.2%，证明了模型的准确性。存在误差的原因是椭圆孔隙在数值离散后，不是标准的椭圆。增加图片分辨率，可以使模拟结果与理论计算结果更接近，但是相应的计算量会增加。

图5 孔隙壁面像素点的状态示意图Fig. 5 The schematic diagram of pixels at pore wall

张睿等[1]通过实验研究了孔隙度随有效应力的变化曲线，本文选取了龙马溪组页岩孔隙度随有效应力的变化曲线进行验证。由于张睿等只考虑了总孔隙度的变化，本文模拟结果也只考虑总孔隙的变化，结果如图9所示。从图中可以看出模拟结果与实验结果相近，实验测得孔隙压缩系数平均值为4.89×10-2MPa-1，本文模拟得到的孔隙压缩系数为4.12×10-2MPa-1，说明模拟结果与实验结果吻合良好。

图6 平面存在椭圆孔隙时各像素点的位移云图Fig. 6 The displacement nephogram of pixels of a plane with an elliptical pore

图7 椭圆孔隙长、短半轴长度随围压变化Fig. 7 The length change of semi-major axis and semi-minor axis of elliptical pore with confining pressures

图8 椭圆孔隙长、短半轴长度随孔压变化Fig. 8 The length change of semi-major axis and semi-minor axis of elliptical pore with pore pressures

图9 孔隙度的应力敏感曲线Fig. 9 Porosity change with effective stress of shale cores

4 页岩数字岩心应力模拟结果与分析

利用本文建立的模型模拟了页岩数字岩心受到应力作用后矿物骨架和有机质各像素点的位移。计算条件为x方向和y方向的应力为20 MPa，孔隙压力为5 MPa。页岩岩样取自四川盆地龙马溪组，有机质的弹性模量取8 GPa[19]，泊松比取0.45，矿物骨架弹性模量取20 GPa，泊松比取0.2。单个像素尺寸为∆x=∆y=70 nm。

图10为页岩数字岩心各像素点的位移云图，值越大表明像素点的位移越大。从图中可以看出对于细长的孔隙，沿短轴方向的位移要比沿长轴方向的大，表明岩石中的细长孔隙更容易沿短轴方向减小，会导致一些细长孔隙闭合或形成几个孤立的孔隙。

图11为矿物骨架孔隙度和有机质孔隙度随围压的变化规律，图12为矿物骨架孔隙度和有机质孔隙度随围压的降低程度。可以发现随着围压增大，矿物骨架和有机质的孔隙度都减小，但是在围压增大时有机质的孔隙度降低程度更大，说明有机质纳米孔对围压更敏感。这是因为有机质的弹性模量小，在受到围压作用时，有机质的应变大，从而挤压孔隙导致孔隙度降低程度大。而矿物骨架支撑能力强，可以承受一部分围压，所以矿物骨架孔隙降低程度相对较小。当围压从10 MPa升高到40 MPa时，矿物骨架孔隙减少了6%，而有机质孔隙减少了6.5%，有机质孔隙减小的程度没有比矿物骨架孔隙减小的程度大很多，是因为矿物骨架承受了大部分的围压，使得围压对有机质孔隙度的降低程度不是很明显。

图10 矿物骨架和有机质各像素点的位移Fig. 10 The displacement nephogram of pixels of matrix mineral and organic matter

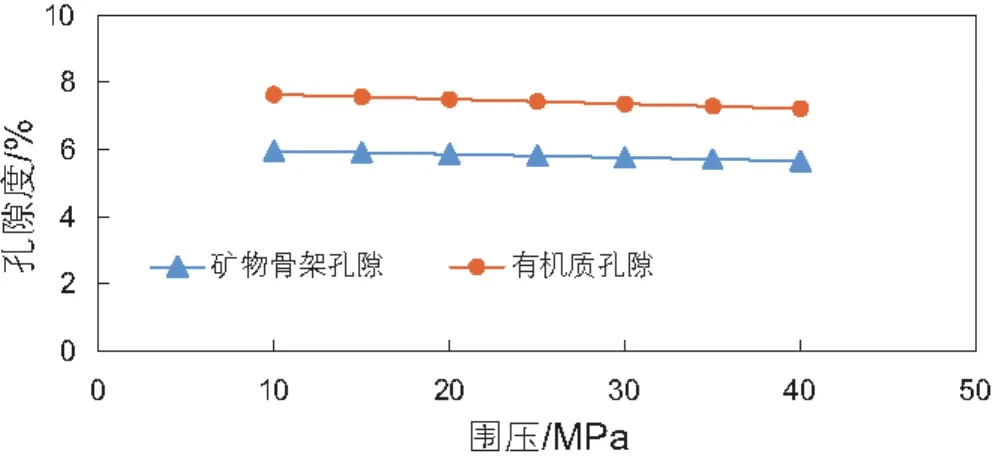
图11 有机质孔隙度和矿物骨架孔隙度随围压的变化Fig. 11 The change of matrix mineral porosity and organic porosity with confining pressures

图12 有机质孔隙度和矿物骨架孔隙度随围压的降低程度Fig. 12 The decrease degree of matrix mineral porosity and organic porosity with confining pressures

图14 有机质孔隙度和矿物骨架孔隙度随孔压的降低程度Fig. 14 The decrease degree of matrix mineral porosity and organic porosity with pore pressures

图13 有机质孔隙度和矿物骨架孔隙度随孔压的变化Fig. 13 The change of matrix mineral porosity and organic porosity with pore pressures

图13为矿物骨架孔隙度和有机质孔隙度随孔压的变化规律，图14为矿物骨架孔隙度和有机质孔隙度随孔压的降低程度。从图中可以看出随着孔压的降低，矿物骨架和有机质的孔隙度都降低，而且有机质孔隙度降低的程度大。这是因为孔隙压力降低时，由于有机质弹性模量小，容易产生形变，导致孔隙变小，孔隙度降低，而矿物骨架孔隙因为矿物颗粒的支撑作用，减轻了孔隙的变形。孔压降低是直接作用于孔隙壁面的，因此有机质孔隙随孔压的变化程度要比随围压的变化程度更加明显，当孔隙压力从17 MPa降低到5 MPa时，矿物骨架孔隙度减少了1.7%，而有机质孔隙度减少了2%。

综上所述，孔压对有机质孔隙的影响最明显。而在生产过程中，地层压力的变化主要是孔隙压力的降低，因此会明显降低有机质纳米孔的孔隙度，从而影响页岩气在有机质纳米孔中的流动。

5 结论

(1)常规数字岩心重构方法一般是基于常压下的扫描电镜图片或CT扫描结果，重构结果与地层条件下的孔隙结构有一定偏差，因此需要对数字岩心进行改进。本文建立的页岩多组分位移计算模型，可以对数字岩心中的矿物骨架孔隙和有机质孔隙进行修正，使数字岩心的孔隙更符合地层实际情况，为页岩气的微观渗流规律研究提供更准确的流动通道模型。

(2)对于比较细长的孔隙，受到应力作用后沿短轴方向的位移要比沿长轴方向的位移大，会导致一些细长孔隙闭合或形成几个孤立的孔隙。

(3)随着围压的增大或孔隙压力的降低，矿物骨架孔隙度和有机质孔隙度都减小。当围压从10 MPa升高到40 MPa时，矿物骨架孔隙减少了6%，而有机质孔隙减少了6.5%；当孔隙压力从17 MPa降低到5 MPa时，矿物骨架孔隙度减少了1.7%，而有机质孔隙度减少了2%。矿物骨架孔隙的变化程度小是因为矿物颗粒可以起到较强的支撑作用。

(4)有机质纳米孔对围压和孔隙压力的比较敏感，是因为有机质弹性模量小，受到应力作用后容易发生形变，挤压纳米孔。其中，孔隙压力对有机质纳米孔的影响较大，会影响到页岩气在有机质纳米孔中的流动，需要进一步研究页岩气在有机质纳米孔中的流固耦合流动规律。

[1] 张睿, 宁正福, 杨峰, 等. 页岩应力敏感实验与机理[J]. 石油学报, 2015, 36(2): 224-231, 237. [ZHANG R, NING Z F, YANG F, et al. Shale stress sensitivity experiment and mechanism [J]. Acta Petrolei Sinica. 2015, 36(2): 224-231, 237.]

[2] 张睿, 宁正福, 杨峰, 等. 微观孔隙结构对页岩应力敏感影响的实验研究[J]. 天然气地球科学, 2014, 25(8): 1 284-1 289. [ZHANG R, NING Z F, YANG F, et al. Experimental study on microscopic pore structure controls on shale permeability under compaction process[J]. Natural Gas Geoscience, 2014, 25(8):1 284-1 289.]

[3] 郭为, 熊伟, 高树生. 页岩气藏应力敏感效应实验研究[J]. 特种油气藏, 2012, 19(1): 95-97. [GUO W, XIONG W, GAO S S.Experimental study on shale stress sensitivity [J]. Special Oil & Gas Reservoirs. 2012, 19(1): 95-97.]

[4] 张磊, 姚军, 孙海, 等. 基于数字岩心技术的气体解析/扩散格子Boltzmann模拟[J]. 石油学报, 2015, 36(3): 361-365. [ZHANG L,YAO J, SUN H, et al. Lattice Boltzmann simulation of gas desorption and diffusion based on digital core technology [J]. Acta Petrolei Sinica, 2015, 36(3): 361-365.]

[5] 张磊, 姚军, 孙海, 等. 利用格子 Boltzmann 方法计算页岩渗透率[J]. 中国石油大学学报(自然科学版), 2014, 38(1): 87-91.[ZHANG L, YAO J, SUN H, et al. Permeability calculation in shale using Lattice Boltzmann Method [J]. Journal of China University of Petroleum, 2014, 38(1): 87-91.]

[6] 王波. 基于数字岩心的页岩气微观渗流研究[D]. 北京: 中国石油大学(北京), 2013. [WANG B. The microscopic percolation study of shale gas based on the digital core [D]. Beijing: China University of Petroleum (Beijing), 2013.]

[7] WU Z H, ZUO Y J, WANG S Y, et al. Numerical simulation and fractal analysis of mesoscopic scale failure in shale using digital images[J]. Journal of Petroleum and Engineering, 2016, 145: 592-599.

[8] LIN W, LI X Z, YANG Z M, et a1. Construction of dual pore 3-D digital cores with a hybrid method combined with physical experiment method and numerical reconstruction method [J]. Transport in Porous Media, 2017, 120: 227-238.

[9] JONES B D, FENG Y T. Effect of image scaling and segmentation in digital rock characterization [J]. Computational Particle Mechanics, 2016, 3(2): 201-213.

[10] JOSHI M. A class of stochastic models for porous media [D]. Kalnsas: University of Kansas, 1974.

[11] HAZLETT R D. Statistical Characterization and Stochastic Modeling of Pore Networks in Relation to Fluid Flow [J]. Mathematical Geology, 1997, 29(6): 801-822.

[12] QUIBLIER J A. A new three-dimensional modeling technique for studying porous media [J]. Journal of Colloid and Interface Science,1984, 98(1): 84-102.

[13] 赵秀才, 姚军, 陶军, 等. 基于模拟退火算法的数字岩心建模方法[J].高校应用数学学报A辑, 2007, 22(02): 127-133. [ZHAO X C,YAO J, TAO J, et al. The digital core modeling method based on simulated annealing algorithm [J]. Applied Mathematics A Journal of Chinese Universities(Ser.A), 2007, 22(02): 127-133.]

[14] OKABE H, BLUNT M J. Prediction of permeability for porous media reconstructed using multiple-point statistics [J]. Physical Review E, 2004, 70: 066 135.

[15] OKABE H, BLUNT M J. Pore space reconstruction using multiple-point statistics [J]. Journal of Petroleum Science and Engineering,2005, 46: 121-137.

[16] WU K J, NAOISE N, JOHN W C, et al. An efficient Markov chain model for the simulation of heterogeneous soil structure [J]. Soil Science Society of American, 2004, 68: 346-351.

[17] WU K J, MARINUS I J, VAN D, et al. 3D stochastic of heterogeneous porous media-applications to reservoir rocks [J]. Transport in Porous Media, 2006, 65: 443-467.

[18] 李荣强, 高莹, 杨永飞, 等. 基于CT扫描的岩心压敏效应实验研究[J], 石油钻探技术, 2015, 43(5): 37-43. [LI R Q, GAO Y, YANG Y F, et al. Experimental study on the pressure sensitive effects of cores based on CT scanning [J]. Petroleum Drilling Techniques, 2015,43(5): 37-43.]

[19] 鞠杨, 王金波, 高峰, 等. 变形条件下孔隙岩石CH4微细观渗流的Lattice Boltzmann模拟[J]. 科学通报, 2014, 59(22): 2 127-2 136. [JU Y, WANG J B, GAO F, et al. Lattice-Boltzmann simulation of microscale CH4flow in porous rock subject to force-induced deformation [J]. Chin Sci Bull, 2014, 59(22): 2 127-2 136.]

[20] 张思勤, 汪志明, 王小秋, 等. 基于MCMC 的数字岩心重建方法[J], 西安石油大学学报(自然科学版), 2015, 30(5): 69-74.[ZHANG S Q, WANG Z M, WANG X Q, et al. Reconstruction of digital core based on Markov Chain-Monte Carlo method (MCMC)[J]. Journal of Xi’an Shiyou University (Natural Science Edition), 2015, 30(5): 69-74.]

[21] 朱益华, 陶果, 方伟. 图像处理技术在数字岩心建模中的应用[J].石油天然气学报, 2007, 29(5): 54-57. [ZHU Y H, TAO G, FANG W. The application of image picture processing technique on digital core modelling [J]. Journal of Oil and Gas Technology, 2007, 29(5):54-57.]

[22] BERNABE Y, BRACE W F, EVANS B. Permeability, porosity and pore geometry of hot-pressed calcite [J]. Mechanics of Materials,1982, 1(3): 173-183.

The modification of modelled two dimensional digital shale under stress

LI Jiangtao1,2, WANG Zhiming1,2, WEI Jianguang3, ZHAO Yanlong1,2, MIN Jian1,2
1 Key Laboratory of Petroleum Engineering of the Ministry of Education, China University of Petroleum, Beijing 102249, China 2 State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum-Beijing, Beijing 102249, China 3 College of Petroleum Engineering, Northeast Petroleum University, Daqing 163000, China

At present, the commonly used numerical reconstruction methods for digital cores are based on the scanning electron microscopy (SEM) images or CT scanning results obtained at atmospheric pressure, which is unrepresentative of the condition of the formation. It is not conducive to analyzing the pore structure of shale and simulating the flow of shale gas in digital rocks. In this paper, a displacement calculation model of shale matrix mineral and organic components has been established based on two dimensional digital rock and rock elastic mechanic equations. The pore structure of the digital rock model was modified under confining stress and pore stress. The effect of stress on pore structure of shale has been studied using the displacement calculation model. The simulation results indicate that the nano pores in organic components are more sensitive to stress. For the slinpores,the displacement along the minor axis is bigger than that along the major axis under stress, which induces the long pores to close or to form some isolated pores. The pore pressure has more significant effect on nano pores, which will affect the shale gas flow in nano pores. The modification of digital core provides an accurate flow path for the future study on shale gas micro seepage flow using the lattice Boltzmann method.

shale; digital core; stress; porosity

*通信作者, wellcompletion@126.com

2016-07-15

国家科技重大专项“多煤层合采全过程流动机理及产能预测研究”( 2016ZX05044005-001)，国家自然科学基金创新研究群体“复杂油气井钻井与完井基础研究”(51221003)，国家自然科学基金“考虑污染条件下页岩气储层气水两相渗流机理研究”(51474070) 和中国石油大学(北京)科研基金（2462017YJRC058）联合资助

李江涛, 汪志明, 魏建光, 赵岩龙, 闵健.应力条件下页岩二维数字岩心的改进研究. 石油科学通报, 2017, 04: 490-499

LI Jiangtao, WANG Zhiming, WEI Jianguang, ZHAO Yanlong, MIN Jian. The modification of modelled two dimensional digital shale under stress. Petroleum Science Bulletin, 2017, 04: 490-499. doi: 10.3969/j.issn.2096-1693.2017.04.045

10.3969/j.issn.2096-1693.2017.04.045

(编辑 马桂霞)