拉幅定型机烘箱内风道的数值模拟与结构优化

刘 佳， 张朱武， 王海朋， 张亚龙

(福州大学石油化工学院， 福建 福州 350116)

拉幅定型机烘箱内风道的数值模拟与结构优化

刘 佳， 张朱武， 王海朋， 张亚龙

(福州大学石油化工学院， 福建 福州 350116)

为改善拉幅定型机烘箱内风道的气流分布和喷嘴出口速度不均匀的现象， 采用Fluent 14.5软件对风道的流场和压力场进行数值模拟， 分析风道的速度矢量图， 计算不同位置喷嘴的出口速度. 模拟计算结果表明： 在风道内等间距安装5块倾斜角为4°的导流板， 并调整风道锥角为3°时， 可以很大程度改善风道内气流分布和喷嘴出口速度的均匀性， 结构优化也较为合理可行.

拉幅定型机； 风道； 导流板； 数值模拟； 结构优化

0 引言

风道作为皮革、 染整等干燥行业中必不可少的设备装置， 是拉幅定型机烘箱内热定型的关键环节之一. 若风道结构设计不合理， 会导致出口风速分布不均匀， 不仅难以保证物料在干燥过程中质量的均一性， 还会延长干燥时间， 增加能耗. 因此， 掌握热气流在风道内的流动特征， 提高喷嘴出口速度的分布均匀性， 对于改善物料干燥效果、 降低能耗具有重要意义[1-2].

目前， 国内外对拉幅定型机内烘箱结构、 换热装置及喷嘴形状及尺寸研究较多. 宋树权等[3]对松弛热定型机腔内三维流场及温度场进行了数值模拟研究， 比较了不同开孔率的均风网对腔内气流组织及温度场的影响， 发现开孔率为5%时的腔内温度均匀性较好， 可减小应力集中， 保证定型机结构寿命. Cay等[4]对拉幅定型机中热气体和热油加热两种方式进行了分析， 结果表明热气体加热方式的效果更好. Kaphahn[5]对拉幅定型机的两种工作空气供给系统方式(旁路系统和风量控制)进行了研究， 指出旁路系统比较适合于如煤气燃烧器等直接热源， 而风量控制系统特别适合用于循环油或蒸气等间接热源系统. 牟国良等[6]设计了一种红外线加热板空气加热装置， 通过对加热装置的二维流场模拟， 发现这种装置不仅能提高热能利用率， 还能使气流和出口温度均匀化分布. 白文华等[7]对印刷涂布烘箱V型条缝喷嘴冲击射流流场进行了数值模拟， 分析了冲击射流中喷嘴高度和宽度对流场分布影响因素， 并设计了较为合理的喷嘴高度和宽度. 徐军等[8]利用流体力学Fluent软件对方孔式、 圆孔式、 条缝式三种不同形状的喷嘴进行了流场仿真分析， 认为不同喷嘴结构应用的适合场合也不尽相同. 目前， 学者对风道的结构设计进行了较多研究， 但对风道内气流分布均匀性的研究较少. 吴成成等[9]对印染热定型机风道进行了流场分析和试验研究， 认为风道端面与风嘴总出风面积相等时， 有利于热定型效率和质量， 但是对风道流场仅停留在定性分析上， 缺乏对风嘴出口风速均匀性的定量分析. 代建武等[10]模拟干燥机气流分配室的流场， 提出3种优化改进方案， 研究结果发现， 平板扰流模型的效果最佳且进行了试验验证与数据分析， 为结构设计提供了参考依据， 但是优化模型过于单一.

本研究利用Fluent软件对风道的气流进行数值模拟分析， 并提出有效的结构优化， 通过对比原始模型和改进模型的流场分布与喷嘴出口速度分布特征， 为拉幅定型机烘箱内风道的结构及类似结构的优化提供理论依据与参考作用.

1 数值模拟

1.1 风道的原始模型

图1 风道局部实物图Fig.1 Image of local air duct

所使用的模型来自某合成革企业的窄缝型喷嘴风道. 由于该风道左右对称， 因此采用对称的半边风道作为计算模型， 这样可以在一定程度上减少计算量， 并且与整个风道作为模型的计算结果偏差较小. 该风道主要由进气端面和23排窄缝型喷嘴等部分组成， 局部实物见图1， 纵截面结构如图2所示. 由图2可见， 进气口位于风道侧面一端， 入口尺寸为450 mm250 mm， 风道长度为4 870 mm， 宽度为800 mm， 右端面高度为250 mm， 左端面高度为60 mm， 上下表面呈一定的锥角α， 风道的上表面封闭， 下表面有23排喷嘴， 喷嘴的间距均为190 mm， 各喷嘴高度为90 mm， 入口为80 mm， 出口为20 mm.

图2 风道的纵截面结构示意图(单位： mm)Fig.2 Longitudinal cross section structure graph of the air duct (unit: mm)

1.2 气体控制方程

对烘箱内风道的速度场进行模拟分析， 暂不考虑温度场的影响， 并假设温度和湿度均为常数. 根据风道内空气的流动状态， 由于流速较低， 可以假设管内流体为不可压缩流体[11]. 由于风道内流体的运动为稳态的黏性流动， 流动状态必须满足基本的守恒方程： 质量守恒方程和动量守恒方程.

质量守恒方程：

动量守恒方程：

式中：xi、xj为坐标分量；ρ为流体密度， kg·m-3；p为流体微元上的压力， N·m-2；ui、uj为速度分量， m·s-1；μ为流体运动粘度， N·s·m-2；δij为函数， 当i=j时，δij=1， 当i≠j时，δij=0.

由于风道内空气的流动状态大多处于完全发展的湍流状态， 尽管RNGk-ε模型与Realizablek-ε模型在处理强旋流或带有弯曲壁面的流动时有一定的优势， 但由于标准k-ε模型足以解决本研究中风道模型的流动问题， 故计算模型采用目前应用最广泛的标准k-ε模型， 壁面区域则采用标准壁面函数法进行处理. 气体流动的湍动能k方程和耗散率ε方程[12]如下：

式中：Gk为由平均速度梯度引起的湍动能k的产生项；μt为湍动黏度系数；C1ε、C2ε、Cμ为经验常数；σk、σε分别为湍动能k和耗散率ε对应的Prandtl数. 在标准k-ε模型中， 根据Launder等的推荐值及后来试验验证， 模型常数分别为C1ε=1.44，C2ε=1.92，σk=1.0，σε=1.3，Cμ=0.09.

1.3 网格划分与边界条件

图3 风道结构及网格示意图Fig.3 Structure and mesh diagram of the air duct

利用ICEM14.5前处理器对风道的物理模型进行网格划分， 由于喷嘴尺寸较小， 对其局部进行网格细化， 整个计算域被划分为1 301 931个网格单元， 1 206 200个节点， 网格示意图如图3所示.

热定型机正常运行时烘箱一区风道内的温度约为160 ℃， 风道入口边界条件采用速度进口， 根据风机风量计算得到入口速度为27 m·s-1， 湍流边界参数采用湍动强度和水力直径， 根据经验公式[13]计算得湍动强度为3.63%， 水力直径为0.16 m； 喷嘴出口边界条件采用压力出口， 设置表压为0 Pa.

1.4 数值计算方法与数据处理

控制方程采用有限体积法进行离散， 速度和压力耦合采用SIMPLIE算法处理， 压力项离散采用标准格式， 动量项、 能量项、 湍流动能和耗散率项离散均采用二阶迎风格式， 除能量方程收敛精度默认为10-6， 其余各参数均设为10-4. 以风道的23个喷嘴出口面作为监测点， 为了更好地定量分析风道内风速分布的均匀性， 建立了一个具有一定参考作用的评定指标[14]. 引入不均匀系数M， 利用M来评价风速的均匀性：

1.5 网格无关性验证与结果分析

在数值模拟中， 网格数量的多少对计算结果精度的影响是不可忽略的. 为了验证本研究中风道模型的网格无关性， 在不改变其它参数的情况下， 通过改变局部网格节点的数量， 比较不同网格数量1 301 931、 2 182 951、 3 166 121的计算结果， 如图4所示. 并将计算结果进行分析对比， 发现模拟的结果误差不超过5%， 在允许范围内. 当网格数量过多时， 对计算机的配置要求更高， 运行更慢， 效率不高， 因此在不影响计算结果的情况下， 以1 301 931网格数作为模拟计算的计算网格.

图5为风道内热气流的三维流线图. 在定常流(即稳态计算时)中， 流线与迹线重合. 由图5可知， 热气流以较大的风速由侧面进风口流入， 沿着风道内X轴负方向向前运动， 大部分热气流经喷嘴出口流出， 其余与封闭端面发生碰撞后返回， 形成一个漩涡. 由于受到进口方向的影响及质点离心力的作用， 靠近外侧空气出现聚集区， 内侧部分区域甚至出现无粒子区， 造成喷嘴出口风速极不均匀. 图6为风道内的压力分布云图. 从图6可知， 在靠近进口端和远离进口端的区域内压力较大， 而喷嘴上流压力取决于风道内压力， 随着压力的增大， 出口流量也会大大增加， 风速也会随之增大， 这就会造成中间区域的喷嘴出口的风速远小于两边. 喷嘴出口1到喷嘴出口23的风速呈现先减小后增大的趋势， 压力图也正好反映出这一点. 图7表示与风道下端面沿Y轴正方向相距1 mm的横截面的速度矢量图， 由于该横截面靠近喷嘴出口， 能清晰地反映流场及出口速度动态， 因此可将该截面作为参考面. 从图7中可以明显地观察到， 靠近内侧的截面区域有一个无粒子区域， 且该区域的风速偏低， 会造成出风风速不均. 同时， 通过对各个监测点的速度进行计算可以发现， 即图4可见， 监测点风速曲线呈U型， 速度波动很大， 不均匀系数M达到70.40%， 这不利于定型机烘箱内物料的干燥， 因此需要对风道进行结构优化.

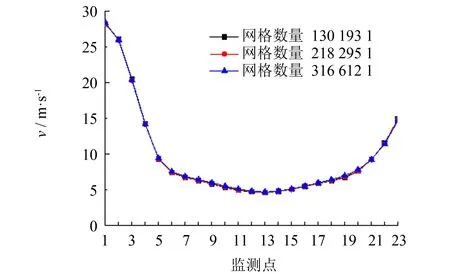
图4 网格无关性验证Fig.4 Neutrality authentication of mesh

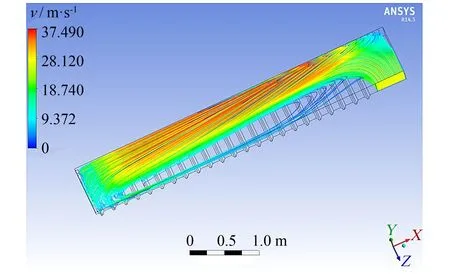
图5 风道内流场分布图Fig.5 Flow field distribution graph of the air duct

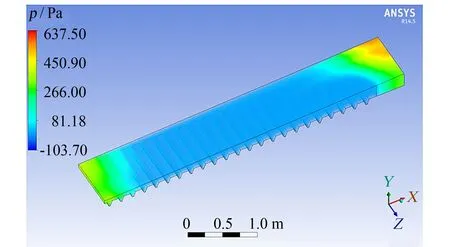
图6 风道内三维压力场分布图Fig.6 Three-dimensional pressure filed distribution graph of the air duct

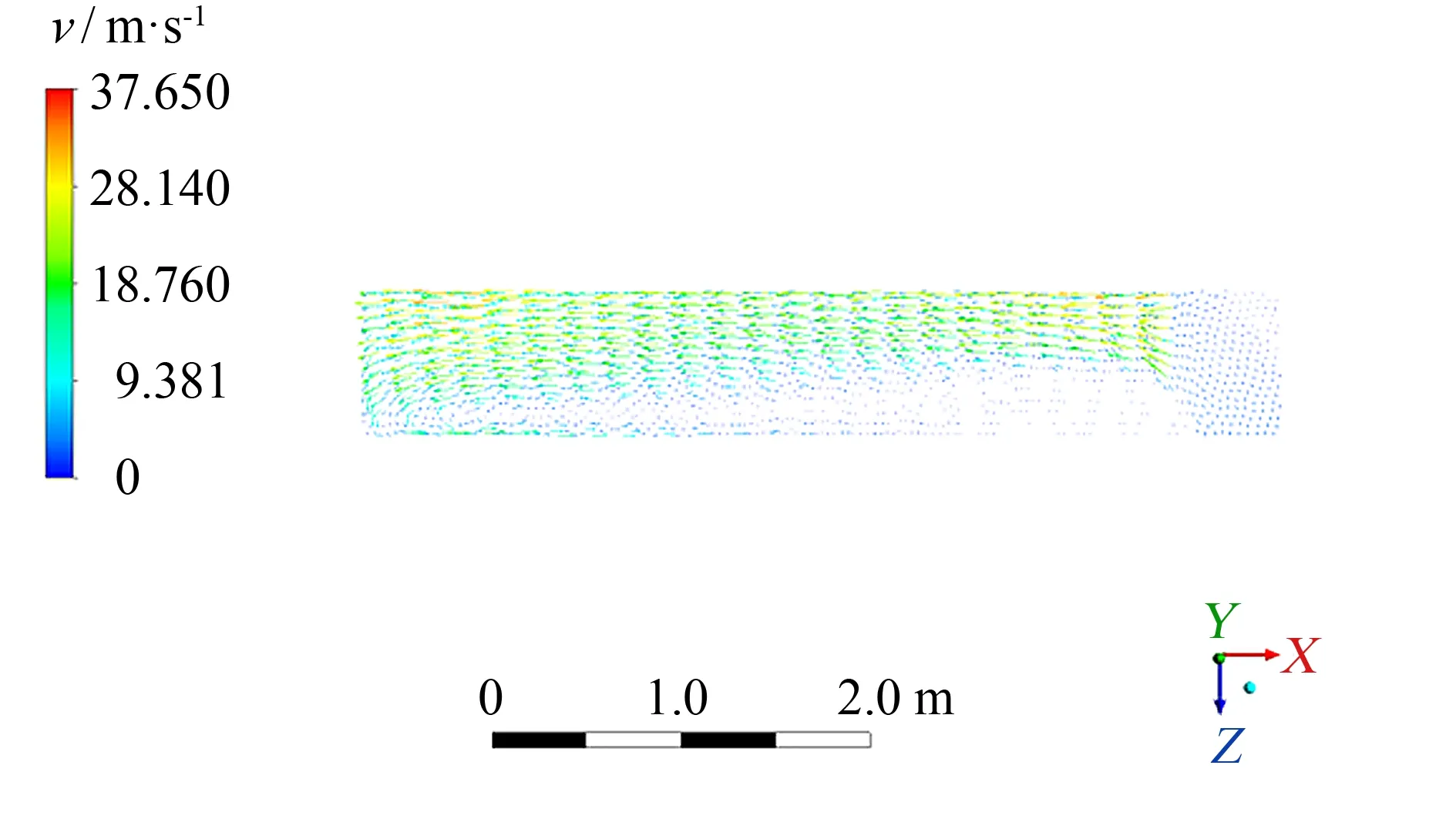
图7 Y=1 mm时截面速度矢量分布图Fig.7 Velocity vector distribution graph with 1 mm Y axle

2 结构优化与仿真分析

2.1 安装导流板

2.1.1 导流板的长度尺寸对流场的影响

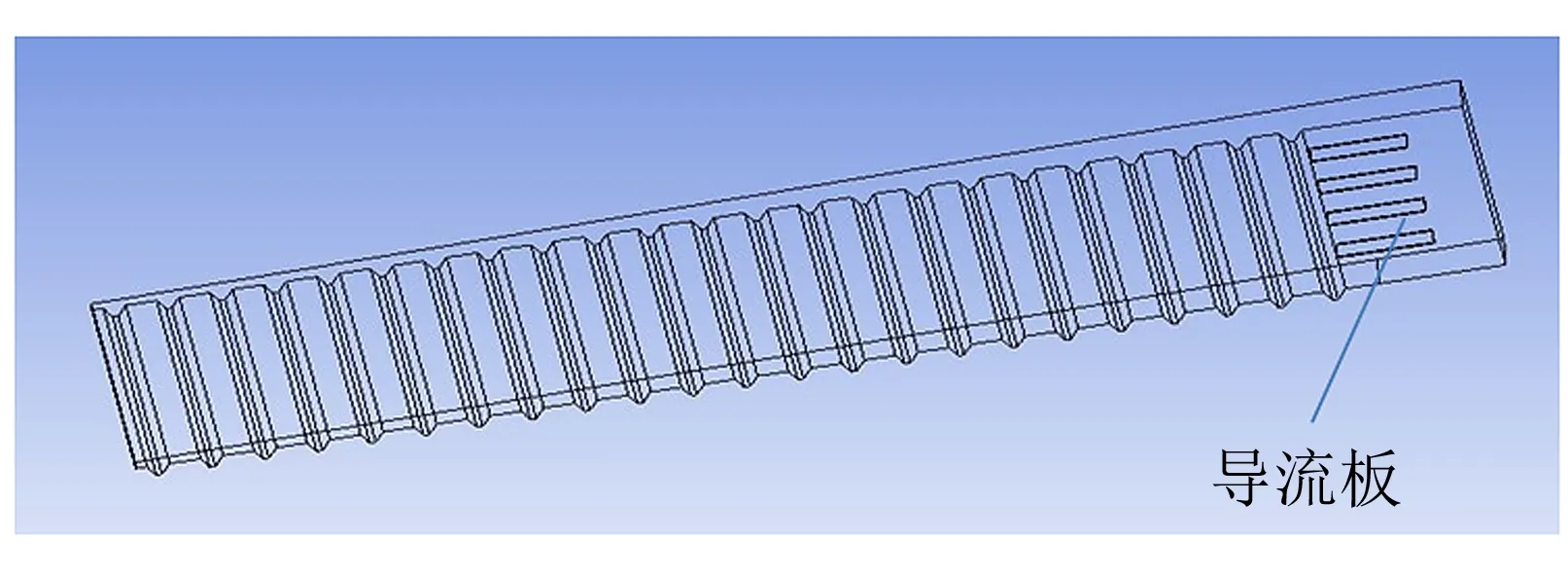
图8 导流板布置方式Fig.8 Guide plates layout

由于导流板具有引流作用， 能使风道内气流分布较为均匀， 且加工安装比较简单、 方便， 研究采用安装导流板的方式来改善风道流场及出口速度均匀性， 并分析导流板的数量及尺寸大小对风道内流场的影响. 导流板数量过多会引起风道内气流流动状态更加紊乱， 增加湍流动能及摩擦损失， 加大能耗， 对于截面面积较大的风道来说， 导流板过少， 导流作用不太明显[15]， 因此安装4块或5块导流板作为改进方式(见图8).

在不影响到喷嘴出口的结构基础上， 多块导流板等间距安装在风道入口处且从下表面垂直插入， 由于导流板的高度过大会造成气流堵塞， 过小导流作用则不明显. 因此， 通过前期模拟分析可确定导流板高度均为125 mm较好， 而导流板的厚度可设为4或5 mm(考虑实际工况)， 导流板的长度范围为120～570 mm.

分别对安装120、 225、 345、 570 mm导流板的风道速度场及各喷嘴出口速度进行模拟计算. 图9为风道流场分布图， 由图9可知， 当安装多块导流板后风道内的气流分布比较均匀， 内侧区域也出现气流聚集区， 有利于出口速度的均匀化. 图10为不同模型喷嘴出口的速度分布对比图. 由图10可知， 当导流板长度不同时， 出口速度分布有所不同， 各喷嘴出口速度曲线整体呈W型. 相比其他长度， 当导流板长345 mm时， 监测点的不均匀系数M为41.74%， 已降到最低. 这是因为， 当长度为345 mm时， 导流板位于喷嘴出口23和进口中间的区域间内， 不仅起到了一个导流作用， 而且导流板的部分区域相当于挡板， 气流撞击导流板后会与来自进口的另一半气流汇合， 在导流板的引流作用下向前运动， 湍流状态更为激烈， 气流在风道内的分布更为均匀， 各喷嘴出口速度总体均值为10.4 m·s-1， 仅次于长度为570 mm的导流板， 但不均匀系数M低于其3.76%； 同时， 计算安装5块导流板时， 选择长度为345 mm的导流板也合适， 但气流的不均匀性比4块只有略微的改善.

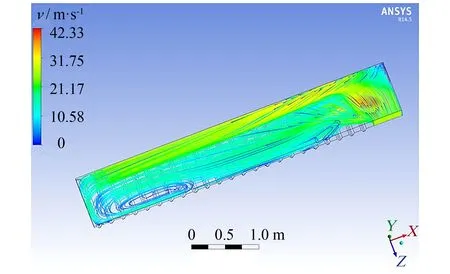
图9 4块导流板长度为345 mm的风道流场分布图Fig.9 Flow flied distribution graph with fours guide plate of long 345 mm

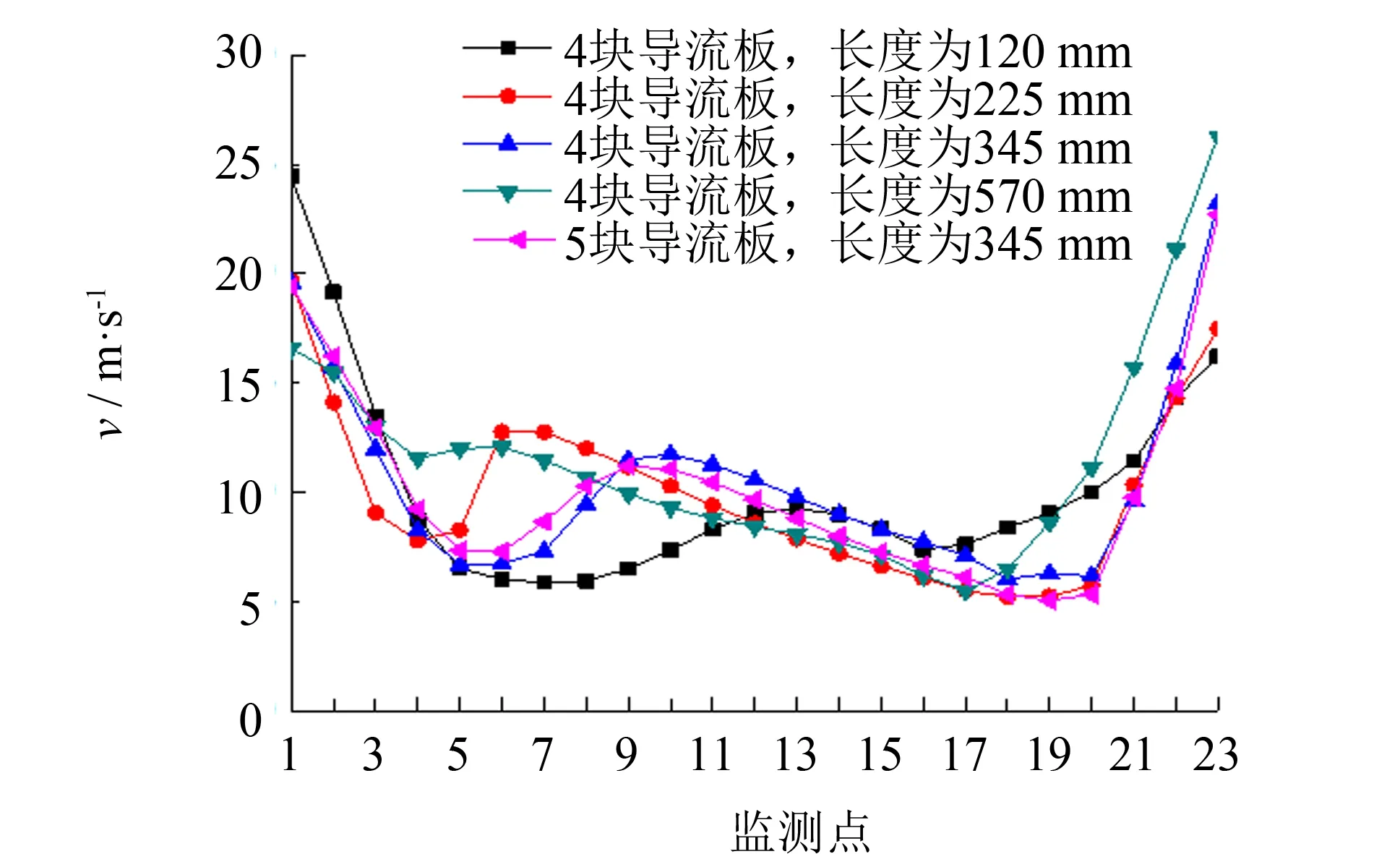
图10 不同模型喷嘴出口的速度分布对比图Fig.10 Nozzles outlets velocity distribution of different model contrast graph

2.1.2 导流板的倾斜角β对流场的影响

以安装4块导流板为主， 分析导流板的倾斜角对流场的影响. 导流板的倾斜角β是导流板与YOZ截面的夹角， 如图11所示. 图12 为倾斜角为4°的截面速度矢量分布图， 由图12可知， 靠近风道外侧的区域速度在20～27 m·s-1之间， 相比内侧区域， 速度场整体都偏大， 喷嘴出口1到出口8之间的区域还出现了一些明显的小型漩涡， 为改善这个现象， 提出改变导流板的倾斜角的改进方案， 对导流板的倾斜角β每间隔4°进行一次建模计算分析.

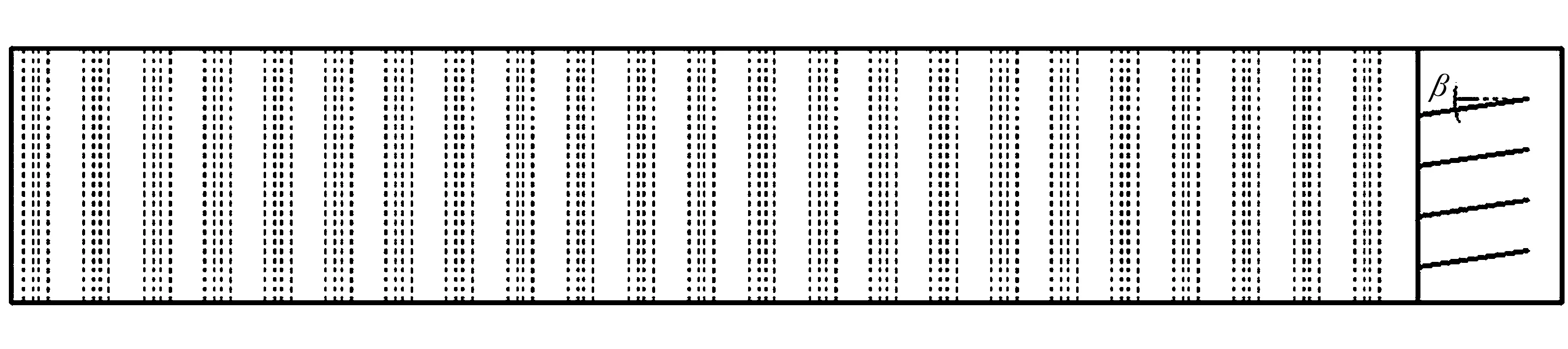
图11 导流板倾斜角的平面示意图Fig.11 Plan graph of guide plates’ title angle

图13为不同倾斜角的喷嘴出口速度分布图. 从图13可以发现， 当导流板倾斜角β分别为0°、 4°、 8°、 12°、 16°时， 各喷嘴出口速度分布曲线仍然呈W型， 总体平均速度在8.9～10.4 m·s-1之间， 不均匀系数M分别为42.68%、 40.35%、 42.31%、 45.53%、 45.77%. 在风道左侧喷嘴出口1到出口8之间有一个较大的波动， 这是由于该区域的气流漩涡导致的. 当导流板倾斜角β为0°时， 喷嘴出口速度波动幅度是最大的. 当倾斜角β为4°， 时， 尽管风道内的漩涡并未得到较大的改善， 但是喷嘴出口的速度波动趋势得到了一定的缓解， 不均匀系数降到最低. 这是由于外侧速度较大的气流在具有一定斜角的导流板作用下， 冲击流速较小的区域， 使风道内流速有所缓和. 但是当倾斜角β大于4°时， 聚集了更多流速大的气流对内侧区域有较大的冲击， 造成出口速度波动较大. 因此， 当导流板倾斜角β为4°时更有利于风道的流场均匀性.

图12 倾斜角为4°的截面速度矢量分布图(Y=1 mm)Fig.12 Velocity vector distribution graph with 1 mm Y axle with 4° title angle

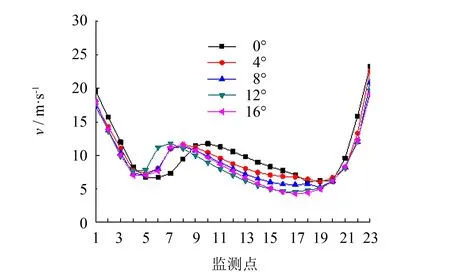
图13 不同倾斜角的喷嘴出口速度分布图Fig.13 Nozzles outlets velocity distribution graph with different title angle

2.2 风道锥角α对流场的影响

为了进一步改善风道气流的分布及出口风速分布均匀性， 对安装导流板后的风道锥角进行分析研究. 在保证进气口风速不变的情况下， 风道锥角α的变化范围为0°～3°. 对风道锥角α每间隔1°进行建模计算， 模拟结果如图14所示.

图15为不同锥角的喷嘴出口速度分布曲线. 图15表明， 当锥角α分别为0°、 1°、 2°时， 各喷嘴出口速度曲线并无太大差别， 整体仍然呈W型， 出口速度仍然不均匀. 通过CFD-Post14.5后处理软件可知， 这些锥角的风道内的气流仍然存在较大的漩涡， 这会延长气流传递路径， 降低物料的干燥效率. 而当锥角α为3°时， 除靠近进口侧的喷嘴22和23外， 喷嘴1的速度偏小， 这是由于喷嘴1出口过于靠近封闭段， 导致其出口流量太小， 从而使喷嘴1出口比平均速度小， 偏差较大. 喷嘴2～21的速度基本保持不变， 出口速度曲线并无较大的波动， 风道内的气流整体分布比较均匀， 原来的漩涡也基本消失， 不均匀系数M降低到31.55%， 这是由于当锥角α为3°时， 风道内的压力基本无变化， 使得出口速度波动较小. 当导流板数量为4或5块时， 两者的计算结果基本无变化， 表明导流板数量基本已到饱和状态. 通过多次对比分析， 导流板数量为5块时， 出口速度更为均匀， 且出口速度整体稍高一些. 因此， 综合考虑后， 当锥角α为3°且安装5块导流板时， 风道内的气流分布及喷嘴出口速度变得更加均匀， 更有利于物料的热定型和干燥效率.

图14 锥角为3°的截面速度矢量图(Y=1 mm)Fig.14 Velocity vector distribution graph with 1 mm Y axle of 3° taper angle

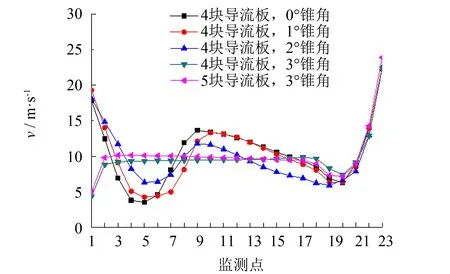
图15 不同锥角的喷嘴出口速度分布曲线Fig.15 Nozzles outlets speed distribution graph with different taper angle

3 结语

对拉幅定型机烘箱内风道的数值进行模拟， 通过增设导流板和改进风道锥角， 改善风道流场及喷嘴出口的风速均匀性， 为实际风道的设计起到参考作用.

1) 在不改变侧面进口的情况下， 在靠近进口的下端面沿宽度方向等间距垂直设置多块导流板， 对风道内的热气流起到了引流作用. 通过模拟分析表明： 安装4块长度为345 mm的导流板时， 气流能获得较好的均匀性， 导流板的数量增加到5块时， 气流的不均性只有略微的改善. 并且， 通过调整导流板斜角β发现， 当斜角β为4°时， 喷嘴出口的速度均匀性得到了最好的改善.

2) 在已安装导流板的风道内， 分析锥角α对风道流场及喷嘴出口速度的影响， 研究发现当风道锥角α为3°且安装5块导流板时， 风道内产生的漩涡基本得到了消除， 各喷嘴出口速度分布最为均匀.

[1] 潘永康， 王喜忠， 刘相东. 现代干燥技术[M]. 北京： 化学工业出版社， 2007.

[2] 高振江. 气体射流冲击颗粒物料干燥机理与参数实验研究[D]. 北京： 中国农业大学， 2000.

[3] 宋树权， 葛友华， 袁铁军， 等. 松弛热定型机腔内三维流场及温度场数值模拟研究[J]. 机械设计与制造， 2011(8)： 93-95.

[4] CAY A, TARAKCOGLU I, HEPBASLI A. Exergetic analysis of textile convective drying with stenters by subsystem models (part 1): exergetic modeling and evaluation[J]. Drying Technology, 2010, 28(12): 1 359-1 367.

[5] KAPHAHN W. Air feed systems in stenter dryers[J]. International Dryer, 1995, 180(2): 10-13.

[6] 牟国良， 张学军， 史增录， 等. 基于CFD的热风加热装置模拟分析与研究[J]. 甘肃农业大学学报， 2014， 49(3)： 125-129.

[7] 白文华， 包能胜， 许鹏， 等. 印刷涂布烘箱V型条缝喷嘴冲击射流流场的数值模拟[J]. 包装工程， 2011， 32(3)： 28-32.

[8] 徐军， 陈海卫， 周一届， 等. 基于Fluent的不同形状烘箱风管流场仿真分析与应用[J]. 轻工机械， 2014， 32(5)： 35-38.

[9] 吴成成， 向忠， 胡旭东. 印染热定型机风道流场分析与试验研究[J]. 浙江理工大学学报， 2016， 35(2)： 218-224.

[10] 代建武， 肖红伟， 白竣文， 等. 气体射流冲击干燥机气流分配室流场模拟与结构优化[J]. 农业工程学报， 2013， 29(3)： 69-76.

[11] 余志勇， 周文， 徐小捷， 等. 竹胶板行业蒸汽烘房的模拟分析与优化[J]. 机电产品开发与创新， 2012， 25(2)： 104-106.

[12] 张师帅. 计算流体动力学及其应用-CFD的软件原理与应用[M]. 武汉： 华中科技大学出版社， 2011.

[13] 杨雪. 单通道滚筒干燥机温度场和流场的数值模拟[D]. 沈阳： 东北大学， 2011.

[14] 韩文霆， 吴普特， 杨青， 等. 喷灌水量分布均匀性评价指标比较及研究进展[J]. 农业工程学报， 2005， 21(9)： 172-177.

[15] 谢振华， 周艳荣. 90°方截面弯管内加装导流板的优化研究[J]. 应用基础与工程科学学报， 2009， 17(4)： 566-573.

Numericalsimulationandstructureoptimizationofairflueinstenteroven

LIU Jia, ZHANG Zhuwu, WANG Haipeng, ZHANG Yalong

(College of Chemical Engineering， Fuzhou University， Fuzhou， Fujian 350116， China)

In order to decrease uneven distribution of airflow and nozzle outlet velocity for air duct in stenter oven, velocity field and pressure field of the air duct were numerically calculated by the Fluent 14.5. Moreover, velocity vector graph and outlet velocity of the nozzle in different positions for the air duct were also analyzed. Finally, the numerical simulation indicated that installing five guide plates with 4° title angle in the air duct by same spaced and adjusting taper angle of the air duct to 3°, which could greatly improved distribution of the airflow and the nozzle outlet velocity and make structural optimization more reasonable and feasible.

stenter oven; air duct; guide plate; numerical simulation; structure optimization

10.7631/issn.1000-2243.2017.05.0706

1000-2243(2017)05-0706-07

TP391.9; TS53

A

2016-08-24

张朱武(1984- )， 副教授， 主要从事高效节能与环保技术方面的研究， zwzhang@fzu.edu.cn

福建省自然科学基金资助项目(2012J05017)

(责任编辑： 洪江星)