饱和电抗器脉冲磁化特性测量分析
2017-12-19张丽萍汪晶慧
张丽萍, 陈 为, 汪晶慧
(福州大学电气工程与自动化学院, 福建 福州 350116)
饱和电抗器脉冲磁化特性测量分析
张丽萍, 陈 为, 汪晶慧
(福州大学电气工程与自动化学院, 福建 福州 350116)
高压直流输电换流阀用饱和电抗器的磁芯工作于脉冲磁化工况, 其分析和设计需要获得脉冲励磁下的磁特性参数. 借助磁脉冲压缩法思路, 利用二阶振荡电路测量其脉冲磁化特性参数, 得到了脉冲激励下的初始磁化曲线和磁滞回线. 利用测量结果计算其等效电感、 饱和时间及磁芯在一个周期内的耗能, 分析磁化速率对磁芯耗能的影响.
脉冲磁化; 磁滞回线; 饱和磁感应强度; 磁化速率; 磁芯损耗
0 引言
高压直流输电是构成坚强电网骨干网架的主要技术手段之一. 直流输电作为成熟可靠的大容量、 远距离、 低损耗输电技术, 在我国乃至全世界的跨区域联网工程中发挥了重要作用. 换流阀是高压直流输电系统的核心装备, 饱和电抗器是换流阀中用来保护晶闸管的重要设备, 饱和电抗器的设计和制造又是换流阀制造中的关键技术之一. 饱和电抗器的工作原理是利用磁芯材料的快速饱和特性, 在晶闸管开通瞬间, 磁芯处于非饱和工作区, 磁导率很高, 阻抗很大, 饱和电抗器承受绝大部分电压, 起到抑制晶闸管开通浪涌电流的作用, 以保护晶闸管; 当饱和电抗器承受大部分电压一段很短时间后(或电流增大到一定程度后), 磁芯快速进入磁饱和状态, 磁导率急剧降低, 阻抗很小, 不影响电路的正常工作. 因此, 饱和电抗器在高磁化速率的磁化过程中电感量的变化是饱和电抗器设计中需要考虑的重要因素.
除此之外, 随着直流输电工程的输送容量不断增大, 饱和电抗器的磁芯损耗也变大, 发热严重. 饱和电抗器的磁芯长期过热会加速其老化, 减少使用寿命, 严重时会造成饱和电抗器失效. 因此, 磁芯损耗也是饱和电抗器设计中的一个重要参数. 在工程应用中常通过测量饱和电抗器的表面温度间接获取饱和电抗器的磁芯损耗, 但表面温度存在着一定的分散性, 因此, 这种方法只能是很粗略地估算磁芯损耗. 国内外学者对饱和电抗器的研究大多基于仿真的电抗器模型的构建[1-2]. 上述对饱和电抗器磁芯损耗的测量和模型分析都没考虑到饱和电抗器高磁化速率工况的影响. 饱和电抗器的感量和磁芯损耗都可由磁化特性获得, 饱和电抗器的磁化过程具有高磁化速率的特征, 这决定了饱和电抗器磁芯的脉冲磁化特性具有特殊性, 直接用静态或者工频的磁参数来指导饱和电抗器的设计和性能分析必然存在较大误差. 为得到饱和电抗器磁芯的脉冲磁化特性参数, 需要测量饱和电抗器实际工况下的电压和电流, 但实际高压大电流工况下饱和电抗器的电压和电流难以测量. 为了获得与实际工况等效的磁化特性参数, 需对其系统进行简化, 搭建适合实验室测量的平台. 饱和电抗器工况具有高磁化速率特点, 这与磁脉冲压缩法[3-12]中非线性电感的工况相似. 磁脉冲压缩法实质上是多级的电阻、 电感和电容串联(RLC)的二阶电路. 饱和电抗器、 晶闸管、 阻尼电容、 阻尼电阻和均压电容组成的换流阀组件本质上也是一个RLC的二阶电路. 因此, 借助磁脉冲压缩法的思路, 搭建用于测量脉冲磁化特性参数的RLC二阶电路.
为获得与实际工况等效的脉冲磁化特性参数, 在保证电抗器磁芯的磁通密度B、 磁场强度H不变的前提下, 减小电抗器体积, 将大体积的电抗器设计为小体积的电感, 增加电感绕组匝数, 从而减小电压和电流, 便于测量. 借助磁脉冲压缩法的思路, 利用储能电容对非线性电感放电的RLC振荡电路测量非线性电感的电压和电流, 获得磁芯脉冲激励下的初始磁化曲线及磁滞回线. 将初始磁化曲线分为不饱和阶段、 饱和阶段及深度饱和阶段, 研究磁化速率对各段感量的影响. 并从磁滞回线中分析一个周期内磁芯的耗能以及磁化速率对耗能的影响.
1 脉冲磁化特性测量电路设计
饱和电抗器实际工作于高电压、 大电流, 难以实测, 需要以降低电压, 减小电流来等效模拟. 为获得与实际工况等效的磁化特性参数, 必须保证模拟工况的磁芯内磁通密度B、 磁场强度H与实际工况一致.
其中:Ae为磁芯横截面积;N为电感的匝数;lg为有效磁路长度;ri、ro分别为磁环内、 外半径.
由式(1)可知, 磁通密度B与电压、 磁芯横截面积、 电感的匝数有关. 降低电压, 为了保持B不变, 可减小磁芯横截面积 . 磁场强度H与激磁电流、 电感的匝数及电感的内外径有关 . 为减小激磁电流可通过增加匝数使H与实际工况相同. 根据模拟工况的电压和电流可算出测量电感的匝数为63匝. 为了确保测量的准确性, 应使磁芯内磁通密度B分布均匀. 当磁芯内外半径之比接近1时, 则可认为磁芯内B分布均匀. 选用厚度为0.08 mm的超薄取向硅钢片绕制成环形磁芯, 尺寸为62 mm × 60 mm × 13 mm.
借助磁脉冲压缩法的思路模拟工况的脉冲磁化特性, 测量电路如图1所示. 其中: C为储能电容; L为被测非线性电感; G为双向可控硅; Rs为电路的等效杂散电阻, 包括导线电阻、 可控硅、 电容及磁芯损耗等效电阻. 让RLC的二阶电路工作在振荡状态, 利用二阶振荡电路产生的反向电流对磁芯去磁. 从图1中的电路可得到下式的方程组:
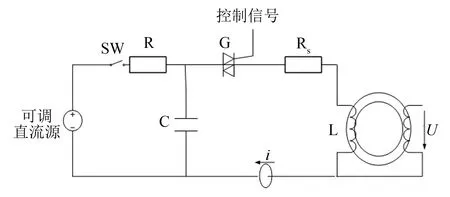
图1 脉冲磁化特性测量电路Fig.1 The circuit for measuring pulse magnetization characteristics
式(2)中微分方程的特征根为:

2 饱和电抗器动态特性测量分析
2.1 初始磁化曲线
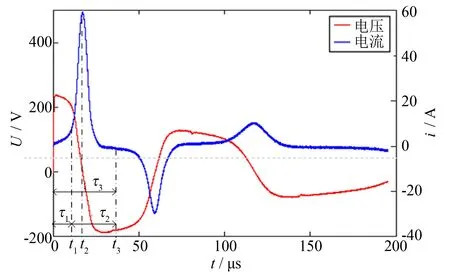
图2 双绕组测量电压、 电流波形Fig.2 Waveforms of voltage and current under double winding test
模拟工况下设计好电感后, 按图1搭建测量电路. 选取满足振荡条件的电容使测量电路产生二阶振荡. 使用电流探头测量原边电流, 为扣除绕组损耗, 电压则取副边绕组感应电压. 图2为1 μF电容充电至250 V, 得到的副边绕组的感应电压u(t)和原边电流i(t)的波形图.
晶闸管导通后, 电容上的电压迅速施加到磁芯上, 电流开始增大. 增大到一定值后, 电感的感量下降, 磁芯上的电压随着电感感量的减小而降低. 图2中电流在t1处出现拐点后电流快速增大. 这是由于电感的磁芯已饱和, 电感的感量变得很小.t2后电流开始减小, 电压反向. 0~t2时间内为磁芯的正向磁化阶段.
由电压和电流波形可获得电感的初始磁化曲线. 改变电容的充电电压就可得到如图3、 4所示的不同磁化速率(dB/dt)下初始磁化曲线. 由图3的初始磁化曲线可将电感的磁化过程分成三个阶段, 从初始到C点为第一阶段, 电感工作于不饱和区, 磁通密度随着磁场强度的增大快速地增大;C点到D点为第二阶段, 电感进入饱和区, 磁通密度增长的速度变缓;D点到磁化过程结束为第三阶段, 电感工作在深度饱和区, 磁通密度随着磁场强度增大略微增加. 由图4的局部放大图可看出随着磁化速率的增加, 初始磁化曲线的上升变缓.
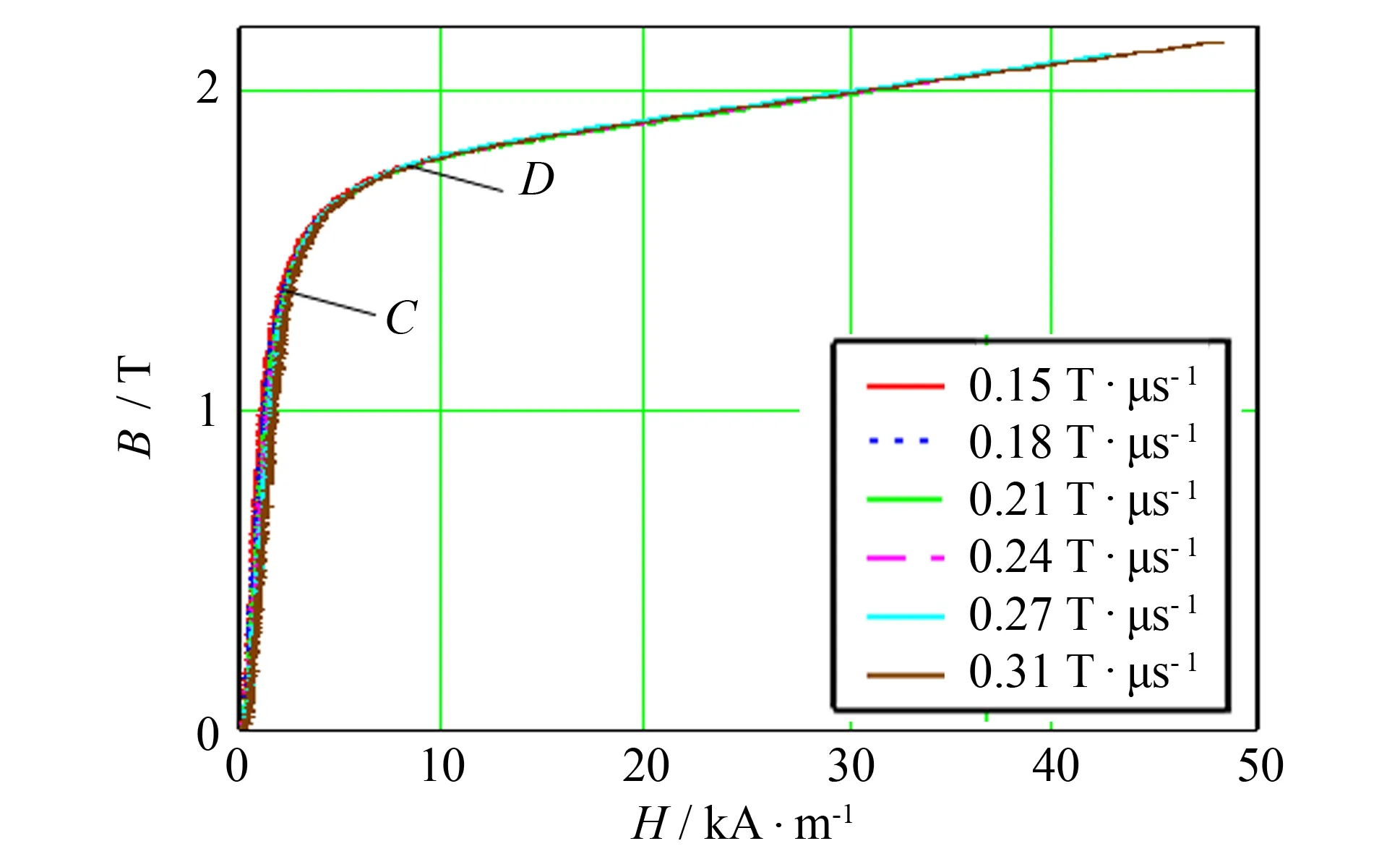
图3 不同磁化速率下的初始磁化曲线 Fig.3 Initial magnetization curve at different magnetization rates

图4 图3的局部放大图Fig.4 Enlargement of Figure 3
2.2 等效相对脉冲磁导率和等效电感
由初始磁化曲线可得到相对脉冲磁导率及电感的感量. 脉冲激励作用下, 磁化速率对相对脉冲磁导率及电感感量的影响尤其明显, 如图5所示. 电感处于非饱和区时, 随着磁化速率的增加, 相同磁通密度B值下的相对脉冲磁导率呈现下降的趋势. 这是由于随着磁化速率的增加, 电感两端的电压升高, 由于电感磁芯相同的B对应的伏秒积一定, 时间变小, 则等效工作频率升高, 磁芯的涡流变大, 涡流的去磁效应增强, 使得磁化电流也变大. 由下式可知,H变大,B不变, 相对脉冲磁导率μr变小. 磁芯进入饱和后, 相同的磁通密度B下相对脉冲磁导率未随着磁化速率的变化而变化. 这是由于磁芯饱和后, 电流不受磁化速率的影响.
式中:μ0为真空的磁导率.
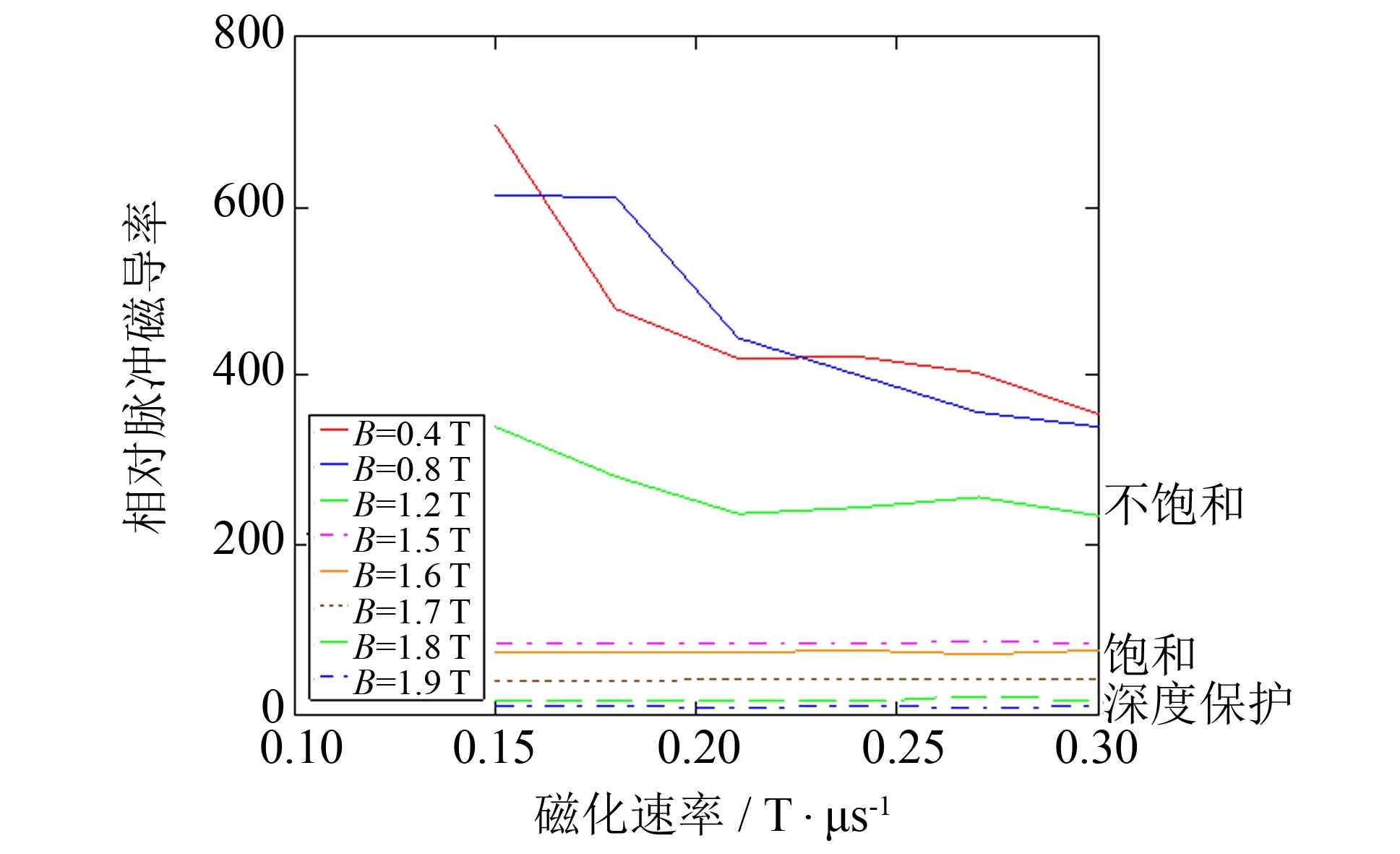
图5 不同磁化速率下的相对脉冲磁导率Fig.5 Relative pulse permeability versus with the magnetization rate
图5中, 当磁化速率为0.15 T·μs-1, 磁芯在不饱和区,B为0.4、 0.8、 1.2 T时所对应的脉冲相对磁导率分别为694、 613、 338. 在饱和与深度饱和区, 不同的B所对应的相对磁导率也相差较大. 因此, 相对脉冲磁导率应采用分区等效的方法来表示电感在不同区的相对磁导率. 等效相对脉冲磁导率定义为, 脉冲激励下磁通密度增量和磁场强度增量的比值.
其中: ΔB为脉冲激励下的磁通密度增量; ΔH为对应ΔB的磁场强度增量.
由式(5)分别算出不饱和区、 饱和区、 深度饱和区的等效相对脉冲磁导率, 再依据下式可分别算出各段对应的感量.
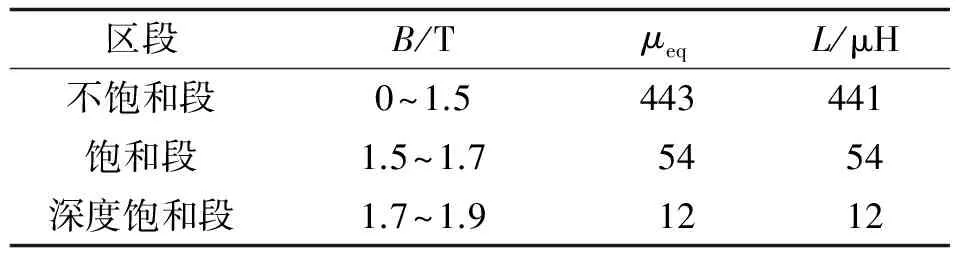
表1 不同磁通密度下电感的感值Tab.1 Inductance under different magnetic flux
式中:μeq为磁芯相对磁导率.
电感在磁化速率为0.15 T·μs-1时, 不饱和段、 饱和段及深度饱和段下的电感值如表1所示. 磁芯饱和后相对磁导率仍会随着磁场强度的增加继续下降. 磁芯深度饱和后其饱和电感感量与空心电感接近. 不饱和段与深度饱和段的电感的感量相差较大, 这样有利于晶闸管在开通过程中起到对电流的抑制作用; 晶闸管完全开通后, 电感的感量很小而不影响电路正常工作.
2.3 饱和时间
电感未饱和时由于感量较大, 会限制电流的上升. 饱和后, 感量急剧下降, 电流快速上升. 电感的饱和时间定义为从施加脉冲激励到电流开始迅速增长的时间. 电感饱和时间的大小直接影响磁芯耗能, 因此, 需要准确地计算饱和时间的大小. 图2中0~t1的时间间隔为电感的饱和时间τ1,t1~t3的时间间隔为τ2, 0~t3的时间间隔为τ3.t3时刻电流值可视为0, 从t3电流值可得到τ3的值.
首先从测出的数据中可粗略估算τ2的值(τ2可视为图2中电流的宽度), 由Ls=(τ2·π-1)2·C-1可算出电感在t1时饱和感量Ls, 由能量守恒得:
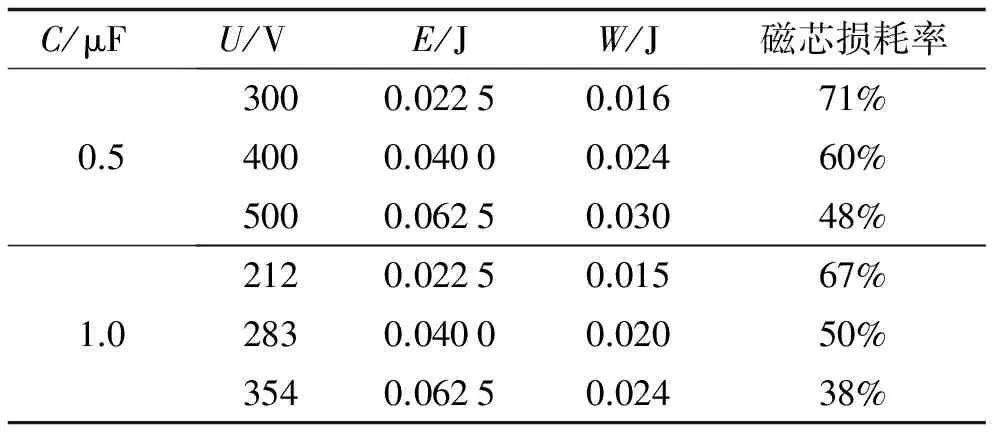
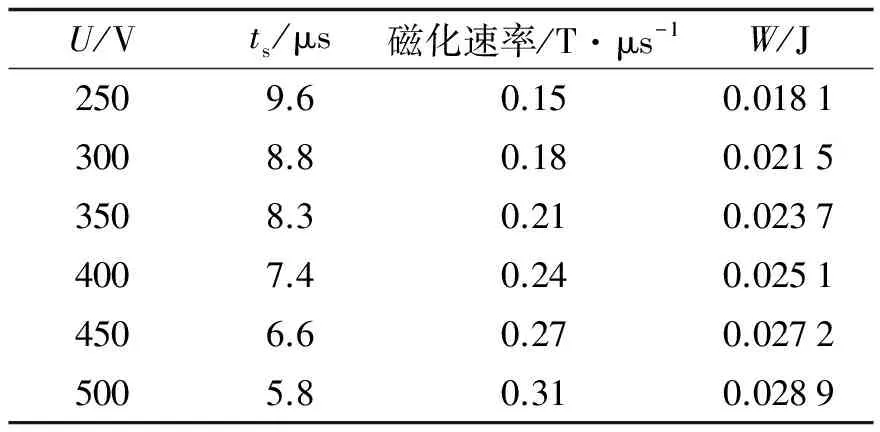
式中:Uτ1、Iτ1分别指的是t1时刻的电压和电流值;Lu是电感在不饱和区的等效感量;Imax是最大电流值. 由于Iτ1< 由式(8)可得到: 通过Uτ1可确定τ1的值, 将此值与τ3-τ2的值相比较, 如果两个值差别很大, 则重新对τ2估值, 重复上述步骤直到τ1与τ3-τ2的值接近为止. 表2算出电容在不同充电电压下的电感饱和时间, 电感饱和时间随磁化速率的增加而变小. 图6 测量得到的磁滞回线Fig.6 Hysteresis loop 由图2中测得的电压和电流算出磁场强度H和磁通密度B, 可得如图6所示磁化速率为0.15 T·μs-1下的磁滞回线. 由磁滞回线面积积分得到此电感的磁芯在一个周期内的耗能为0.018 J. 通过改变电容电压, 可以得到如表2所示的不同磁化速率下测量电感磁芯耗能值. 随着电容电压的升高, 磁芯磁化速率增大, 磁芯等效工作频率变高, 涡流增大, 磁芯损耗也随之变大. 为分析磁芯耗能与充电电容能量的关系, 选取0.5、 1.0 μF两种电容, 调整充电电压, 使得电容充电能量相等, 计算电感磁芯耗能占总能量的比例. 如表3所示, 同一电容, 随着充电能量的增加, 磁芯耗能也增加, 但磁芯耗能占总能量的比例下降. 相同的充电能量下, 充电电压(即磁化速率)越大, 磁芯耗能越大. 表2 不同磁化速率下的磁芯损耗Tab.2 Core loss with the magnetization rate 表3 相同充电能量不同充电电压下的磁芯耗能Tab.3 Core loss for different voltage under the charge energyenergy 1) 采用RLC二阶振荡法获得了不同磁化速率下的速饱和磁芯的初始磁化特性曲线. 2) 在脉冲激励下, 磁芯的非饱和与饱和相对磁导率变化比较剧烈, 电感量也随着变化, 因此采用等效非饱和电感与等效饱和电感来表征脉冲激励电感的感量. 3) 磁芯耗能随着磁化速率的升高而增加. 4) 在相同的电容下, 磁芯耗能随着充电能量的增大而增大, 但总的充电能量所占的比例却变少. [1] 纪锋, 曹均正, 陈鹏, 等. HVDC整流侧阀饱和电抗器铁损仿真研究[J]. 电网技术, 2014, 38(10): 2 680-2 684. [2] 纪锋, 陈鹏, 魏晓光, 等. HVDC换流阀用饱和电抗器的建模及仿真[J]. 智能电网, 2013, 1(2): 65-69. [3] 张东东, 严萍, 王珏, 等. μs级脉冲激励下磁开关磁芯磁特性[J]. 高电压技术, 2009, 35(1): 87-92. [4] BURDT R, CURRY R D. Magnetic core test stand for energy loss and permeability measurement at a high constant magnetization rate and test for nanocrystalline and ferrite materials[J]. Review of Scientific Instruments, 2008, 79: 094 703. [5] ROSHEN W A. A practical, accurate and very general core loss model for nonsinusoidal waveforms[J]. IEEE Transactions on Power Electronics, 2007, 22(1): 30-40. [6] CHOI J, NAMIHIRA T, SAKUGAWA T. Simulation of 3-staged MPC using custom characteristics of magnetic cores[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2007, 14(4): 1 025-1 032. [7] 丁臻捷, 苏建仓, 丁永忠, 等. 环形磁芯快脉冲动态参数测量方法[J]. 强激光与粒子束, 2004, 16(10): 1 343-1 346. [8] 张国伟, 丛培天, 乔开来, 等. 脉冲磁化条件下非晶磁芯的损耗特性[J]. 强激光与粒子束, 2012, 24(5): 1 247-1 250. [9] 饶俊峰, 邱剑, 刘克富. 脉冲压缩电路磁开关动态特性[J]. 强激光与粒子束, 2012, 24(4): 859-862. [10] ZHU J G, HUI S Y R, RAMSDEN V S. A dynamic equivalent circuit model for solid magnetic cores for high switching frequency operations[J]. IEEE Transactions on Power Electronics, 1995, 10(6): 791-795. [11] 王瑞华. 脉冲变压器设计[M]. 北京: 科学出版社, 1996: 204-243. [12] CHOI J, NAMIHIRA T, SAKUGAWA T. Loss characteristics of a magnetic core for pulsed power applications[J]. IEEE Transactions on Plasma Science, 2007, 35(6): 1 791-1 796. Measurementandanalysisofpulsemagnetizationcharacteristicsofmagneticcoreofsaturablereactor ZHANG Liping, CHEN Wei, WANG Jinghui (College of Electrical Engineering and Automation, Fuzhou University, Fuzhou, Fujian 350116, China) The working condition of HVDC converter valve’s saturable reactor is micro-second pulse excitation. In the design of the magnetic core, the magnetic characteristics under fast pulse magnetization need. In order to obtain the initial magnetization curve ofB-Hand hysteresis loop, the magnetic characteristics under fast pulse magnetization is measured by using RLC resonant circuit. The equivalent inductance, saturated time and energy dissipation of magnetic core in one cycle are calculated by the measured results. The magnetizing rate has influence on the energy dissipation of the core. The characteristics are of great significance to the optimal design of saturable reactor. pulse magnetization; magnetic hysteresis loop; saturation magnetic induction intensity; magnetization rate; core loss 10.7631/issn.1000-2243.2017.05.0663 1000-2243(2017)05-0663-05 TM474 A 2017-03-17 张丽萍(1977-), 讲师, 主要从事电力电子功率变换技术、 高频磁技术研究, leep-zh@163.com 福建省自然科学基金资助项目(2016J01217, 2015J01191) (责任编辑: 沈芸)2.4 磁芯能耗

3 结语
