一种采用不变矩的矢量面目标匹配方法
2017-12-19温伯威马京振
温伯威,孙 群,马 超,马京振
(信息工程大学,河南 郑州 450001)
一种采用不变矩的矢量面目标匹配方法
温伯威,孙 群,马 超,马京振
(信息工程大学,河南 郑州 450001)
不变矩作为理想的形状描述子,具有平移、旋转、缩放变换不变的特点。以M. K. HU矩方法为基础,提出一种采用不变矩的矢量面目标匹配方法。该方法以7个矩不变量组成矢量面目标的特征向量,通过度量矢量面目标与候选面目标特征向量之间的欧式距离判定同名实体。对两种不同数据源中水域面目标进行匹配实验,验证该方法的有效性。
形状描述子;不变矩;匹配;面目标;同名实体
在基础地理空间数据生产和更新实践中通常需要利用大量的多源数据,这些数据在语义描述、几何位置、数据格式等方面存在着诸多的不一致性问题,给多源数据的综合利用带来极大困难。基于目标特征进行相似性匹配是解决多源空间数据不一致性问题的主要手段和方法,通过目标匹配实现多源数据信息互补、改善数据质量、扩展数据应用范围[1]。
匹配技术广泛应用于模式识别、计算机视觉、数据库更新与维护、图像分析与理解等领域[2-3]。学者将匹配技术引入到地理信息科学领域,在多源空间数据集成和融合[4-5]、空间数据库多尺度表达和更新[6]、基于位置服务的导航[7-8]等方面取得一定成果。从判别依据上可以将空间目标匹配方法分为几何匹配、语义匹配、拓扑匹配[9-10]。无论采用何种方法都需要提取空间目标的特征,空间目标特征提取的优劣直接影响匹配算法的科学性和合理性。如何提取出一种既能反映空间同名实体之间联系又不随几何变换(平移、旋转、缩放)变化的特征成为空间目标匹配的关键。
面目标在基础地理空间数据中占有相当大的比重,在基础地理数据生产和更新实践中若能实现面目标的自动匹配将会大大降低劳动强度,缩短生产周期。不变矩[11]是描述图形图像形状的重要参数,不随原始图形图像的几何变换而发生变化,在场景匹配、飞机识别、字符识别、图像配准和识别领域具有广泛应用。本文将不变矩应用到矢量面目标匹配中,通过基于不变矩的相似性计算识别出面目标同名实体。
1 面目标形状描述子
1.1 形状描述子
形状是面目标的本质特征之一,是面目标几何匹配的重要特征。面目标间的相似度是进行几何匹配的主要依据,其关键是构造面目标的形状描述子[12]。面目标的形状描述子可以分为全局性描述子和局部性描述子。全局性描述子反映的是目标的全局特征,主要包括面积、周长、方向、角度、紧致性、实心度、偏心率、外接矩形等[13];局部性描述子反映的是目标的局部特征,主要包括特征点、凸凹结构、弧段链等。上述形状描述子都能从不同层面反映面目标的特征,但这些形状描述子都具有局限性,应用于面目标相似性度量各有优缺点。在面目标识别、匹配领域,理想的面目标形状描述子应该具有不随几何变换(平移、旋转、缩放)变化的特点。
1.2 图像不变矩
矩源于统计学,常用来描述随机变量的空间分布特征,在物理学中矩用来表征物质的质量分布。设二维连续随机函数F(x,y)的概率密度分布函数为f(x,y),则F(x,y)的(p+q)阶原点矩mpq的定义为
(1)
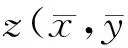
(2)
式中:m00表示图像的零阶矩;m10和m01为图像的一阶矩。
(3)
标准化的中心矩Ipq定义为
(4)
标准化中心矩Ipq具有平移、缩放双重不变特点,但不具备旋转不变的特点。M. K. HU于1962年通过对较低阶数的中心矩进行线性组合,得到一套具有平移、旋转、缩放不变特点的矩不变量(即不变矩),这些不变矩的表达式为
(5)
(6)
(7)
(8)
(9)
(10)
(11)
M. K. HU提出的矩不变量是针对图像区域本身的,具有与图像灰度值密切相关、计算量大等特点。在面目标识别中,反映面目标本质特征的是轮廓,而不是灰度,因此,M. K. HU矩方法有时并不能有效反映面目标的形状特征。R. Y. Wong[13]在M. K. HU研究的基础上提出离散条件下的矩提取方法。
设离散数字图像f(m,n)的尺寸为M×N,其p+q阶矩和中心矩的表示为
(12)
(13)
式中,p,q=0,1,2…。
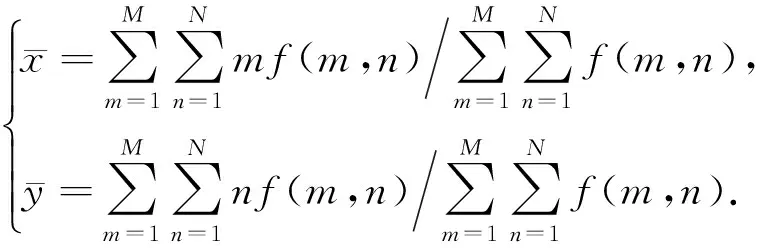
(14)
标准化中心矩Ipq的定义为
(15)
这里γ取值为1+p+q而不是HU矩方法中的(2+p+q)/2。刘亦书[12]等证明轮廓矩不变量同样具有平移、旋转、缩放不变的特点。将式(15)分别代入式(5)~式(11)能够得到轮廓曲线的7个矩不变量。
1.3 矢量图形不变矩
在研究图像区域不变矩与图像轮廓不变矩的基础上,针对工程设计与机械制造领域有大量矢量图形需要识别匹配的问题,曹明[15]提出矢量图形不变矩的构造方法。构造方法为
设G为矢量图形,V={v1,v2,v3,…,vn}为G特征点的集合,(xi,yi)为特征点vi的坐标,n为特征点的个数。矢量图形G的原点矩和中心矩定义为
(16)
(17)
(18)
对μpq进行标准化得到G标准中心矩Ipq,表达式为
(19)
将式(19)分别代入式(5)~式(11)可以得到矢量图形的7个不变矩。
2 基于不变矩的矢量面目标匹配模型
在基础地理信息生产与更新领域,通常需要对来自不同部门、不同时期生产的、不同尺度的多源矢量数据进行融合,生成几何精度高、属性信息丰富、现势性强的基础地理信息。面目标识别、匹配是多源矢量数据融合的重要内容,同时也是多源矢量数据融合的难点。由于几何精度、制图综合等原因,面状同名实体在空间位置、几何形状等方面存在着差异,这些差异使得采用常规的几何匹配方法难以识别出多源矢量数据中的面状同名实体。不变矩作为矢量面目标的形状描述子,具有平移、旋转、缩放不变的特点,这些特点较好地满足了矢量面状同名实体识别、匹配的需求。因此,本文基于矢量图形矩不变量建立面目标匹配模型,具体思路如下:
设R为矢量数据源S中的面目标,R′为矢量数据源S′中的待匹配面目标,按照上文方法分别求得R和R′的7个矩不变量,以这7个矩不变量分别组成R和R′的特征向量a和b。
特征向量a和b之间空间距离可以采用Euclidean距离、Manhattan距离、Mhalanobis距离以及Hausdorff距离进行度量,这里采用欧氏距离计算特征向量a和b之间的距离。特征向量a和b之间的EuclideanD(a,b)可以表示为
(22)
矢量面目标R和待匹配矢量面目标R′之间的相似性可以通过两者的特征向量a和b之间的EuclideanD(a,b)进行度量。当D(a,b)越小时,两者的形状差异性越小,形状相似性越大;当D(a,b)越大时,两者的形状差异性越大,形状相似性越小;当D(a,b)为零时,两者的形状相似性为1,即两者形状完全相似。在矢量面目标匹配过程中,当矢量面目标R和待匹配矢量面目标R′的特征向量a和b之间的EuclideanD(a,b)为最小值时,即判定两者为同名实体。
3 实验与分析
本文选取某地区不同时期生产的两种比例尺均为1∶25万的数据源S和S′。数据源S采用的坐标系为北京1954,数据源S′采用的坐标系为2000中国大地坐标系(CGCS2000),数据源S′的现势性优于S。在对两种数据源数学基础进行统一的基础上,首先对矢量图形不变矩具有平移、旋转、缩放不变的特点进行验证,其次采用基于不变矩的面目标匹配方法对数据源S和S′中水域面状目标进行匹配实验。
选取数据源S中的水域矢量面目标R1,分别对其进行平移、旋转、缩放操作,将得到的矢量面目标分别记为R2,R3,R4,如图1所示。分别计算R1,R2,R3,R4的7个矩不变量,计算结果如表1所示,通过对比可以发现水域矢量面目标R1的在平移、旋转、缩放操作后,其矩在有效数字范围内确实未发生变化。

图1 水域矢量面目标R1,R2,R3,R4
从数据源S中随机选取10个水域面目标,分别记为:A1,A2,A3,…,A10,这些面目标在数据源S′中对应的同名实体分别记为:B1,B2,B3,…,B10。分别计算这些水域面目标的7个矩不变量,将7个矩不变量组成水域面目标的特征向量,按照矢量面目标匹配模型,分别计算数据源S中的面目标与S′中的面目标之间的欧氏距离,计算结果如表2所示。表2中的数值为数据源S与S′中水域面状目标之间的欧氏距离,对角线上的数值为对应同名实体之间的欧式距离,例如:A1与B1,B2,B3,…,B10之间的欧式距离分别为:(0.213 59,0.317 38,0.707 34,0.879 19,1.082 51,3.860 93,0.811 14,0.556 71,1.552 20,1.500 67)(单位:×1010)。从表2可以看出,除A9与B9这对同名实体之间的欧式距离不是A9与B1,B2,B3,…,B10之间欧氏距离的最小值外,其余同名实体间的欧式距离都是对应列的最小值。
采取人工方式比对A9与B1,B2,B3,…,B10之间的形状差异可以发现,A9与B3之间的形状差异最小,但两者并非同名实体。因此,可以得出如下结论:①矩不变量对形状特征较为敏感,当同名实体间的形状差异不大时,采用不变矩判定多源地理空间数据中的矢量面状同名实体比较有效。②仅采用不变矩进行矢量面目标匹配可能会造成误匹配,为了提高同名实体匹配的查准率,可以结合基于面目标空间位置的匹配方法(如基于面目标质心的匹配方法)一起使用,减少同名实体误匹配的概率。

表1 R1,R2,R3,R4的7个矩不变量
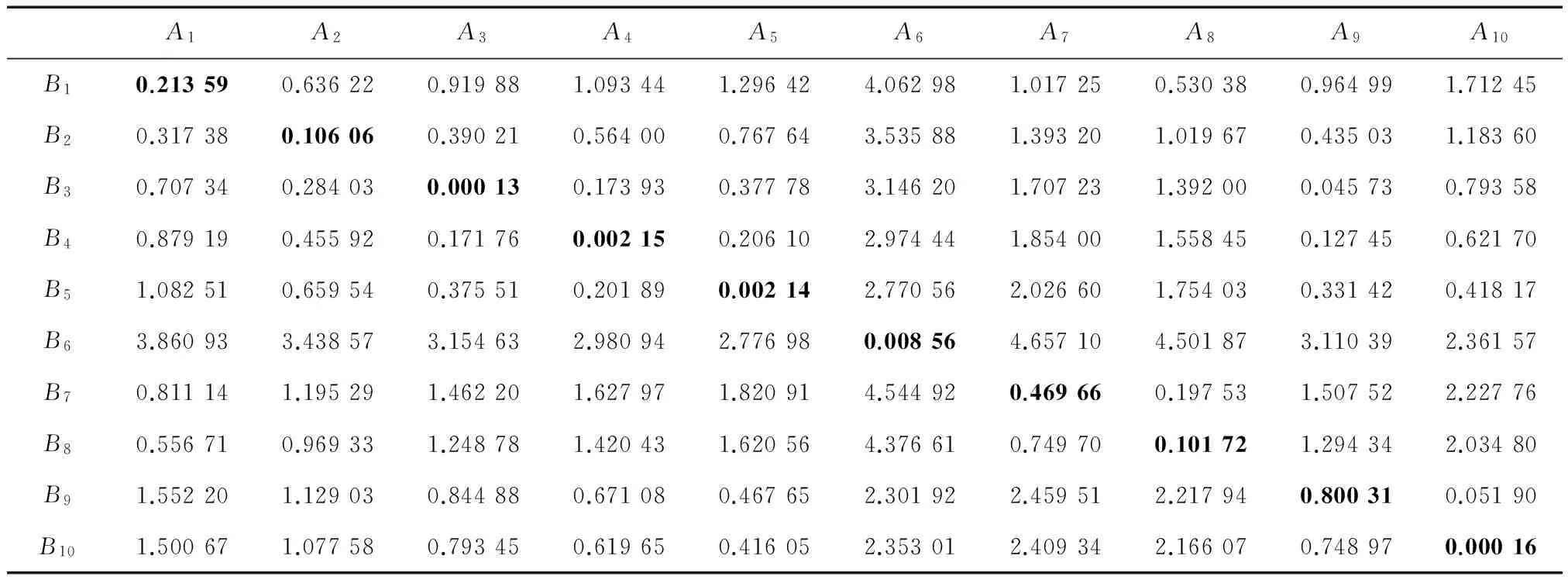
表2 数据源S与S′中水域面状目标之间的欧氏距离 ×1010
4 结 论
本文在深入研究M. K. HU图像区域不变矩与图像轮廓不变矩的基础上,提出一种采用不变矩的矢量面目标匹配方法。该方法以M. K. HU矩方法中7个矩不变量组成矢量面目标的特征向量,通过度量矢量面目标特征向量与候选匹配面目标特征向量之间的距离进而确定同名实体,以某地区不同时期生产的两种比例尺均为25万数据源中的水域面目标进行实验,验证基于不变矩的矢量面目标匹配方法的有效性,同时亦指出该方法的局限性:当同名实体间的形状差异较大时,基于不变矩的矢量面目标匹配方法确定的同名实体可能存在误匹配。
[1] 赵彬彬, 邓敏, 徐震, 等. 多尺度地图面目标匹配的统一规则研究[J]. 武汉大学学报(信息科学版), 2011,36(8):991-993.
[2] AMIT Y, GEMAN D, FAN X. A Coarse-to-fine Strategy for Multi-class Shape Detection[J]. IEEE Transactions on Patterns Analysis and Machine Intelligence, 2004, 26(12): 1606-1621.
[3] 于家城, 陈家斌, 晏磊, 等. 图像匹配在海底地图匹配中的应用[J]. 北京大学学报(自然科学版), 2007, 43(6): 733-737.
[4] 安晓亚, 孙群, 尉伯虎. 利用相似性度量的不同比例尺地图数据网状要素匹配算法[J]. 武汉大学学报(信息科学版), 2012,37(2):224-228.
[5] 赵东保, 盛业华, 张卡. 利用几何矩和叠置分析进行多尺度面要素自动匹配[J]. 武汉大学学报(信息科学版), 2011,36(11):1371-1374.
[6] 王育红. 面向更新信息提取与集成的空间实体匹配方法[J]. 测绘科学, 2011,36(1):128-130.
[7] STIGMAR H. Matching Route Data and Topographic Data in a Real-time Environment[C]. Proceedings of the 10thScandinavian Research Conference on Geographical Information Science, 2005:13-15.
[8] QUDDUS M A, OCHIENG W Y, NOLAND R B. Map Matching Algorithms for Intelligent Transport Systems Applications[C]. Proceedings of the 13thWorld Congress on Intelligent Transport Systems and Services, London, 2006.
[9] 付仲良, 逯跃锋. 利用弯曲度半径复函数构建综合面实体相似度模型[J]. 测绘学报, 2013,42(1):143-150.
[10] 陈换新, 孙群,肖强,等.空间数据融合技术在空间数据生产及更新中的应用[J]. 武汉大学学报(信息科学版), 2014,39(1):117-121.
[11] AL-BAKRI M. Developing Tools and Models for Evaluating Geospatial Data Integration of Official and VGI Data Sources[D]. Newcastle: Newcastle University,2012:109-114.
[12] 张显全, 郭明明, 唐莹, 等. 一种新的几何特征形状描述子[J]. 计算机工程与应用, 2007,43(29):90-92.
[13] 潘泉, 程咏梅, 杜亚娟,等. 离散不变矩算法及其在目标识别中的应用[J]. 电子与信息学报, 2001,23(1):30-34.
[14] 刘亦书, 杨力华, 孙倩. 轮廓矩不变量及其在物体形状识别中的应用[J]. 中国图像图形学报, 2004,9(3):308-312.
[15] 曹明. 不变矩在矢量图形识别中的应用[D].大连:大连理工大学, 2008.
[责任编辑:张德福]
A matching method of vector area object using invariant moments
WEN Bowei, SUN Qun, MA Chao, MA Jingzhen
(Information Engineering University, Zhengzhou 450001, China)
Invariant moment is a perfect shape descriptor, which has the invariant characteristic under transformation (translation, rotation,scale). Based on the method of M. K. HU moments, a matching method of vector area object using invariant moments is proposed in this paper. In this method, the eigenvector of vector area object consists of seven moment invariants, and the same entity is judged through measuring the Euclidean distance between the eigenvector of vector area object and the eigenvector of candidate vector area object. A similarity matching experiment between the water area objects from different data sources is made, and the experiment results validate the proposed method.
shape descriptor; invariant moment; matching; area object; same entity
10.19349/j.cnki.issn1006-7949.2017.02.002
2016-04-09
国家自然科学基金资助项目(41201391;41571399)
温伯威(1986-),男,博士研究生.
P208
A
1006-7949(2017)02-0005-04
引用著录:温伯威,孙群,马超,等.一种采用不变矩的矢量面目标匹配方法[J].测绘工程,2017,26(2):05-08,13.
