我国金融机构系统性风险动态监测
——基于CCA和动态因子copula模型的研究
2017-12-19王培辉
王培辉,袁 薇
(河北大学经济学院,河北 保定 071002)
我国金融机构系统性风险动态监测
——基于CCA和动态因子copula模型的研究
王培辉,袁 薇
(河北大学经济学院,河北 保定 071002)
本文结合未定权益分析法和动态因子copula模型研究了2008年1月至2016年3月我国金融机构系统性风险。研究结果表明:(1)基于未定权益分析法计算的信用价差指标较好地揭示了单一金融机构违约风险动态变化,次贷危机期间较高,2015年以来再次升高,具体来看,证券公司最高,保险公司和信托公司居中,银行最低。(2)基于动态因子copula模型计算的系统性风险指标较好地反映了我国金融机构系统性风险演进,2009年下半年至2014年底系统性风险较高,样本期间内金融机构在系统重要性上没有显著差异。比较发现单一金融机构违约风险较高,并不意味着系统性风险高,这取决于金融机构间相依结构。因此,加强金融机构宏观审慎监管时,应关注金融机构间相依结构动态变化。
系统性风险;未定权益分析法;动态因子copula模型
一、引 言
自2007年次贷危机爆发以来,金融机构稳定性和系统性风险监测已经成为各国中央银行的一项关键任务,并发展成为各国货币政策目标。次贷危机的一个突出特点是之前独立运动的金融资产,危机期间突然同时波动变化,金融资产间相依结构发生变化,协动性明显增强。危机后新的审慎监管更加关注金融资产协动性带来的系统性风险。这需要描述金融资产收益率的联合分布,以估计它们之间的相依结构,然而在现代金融时间序列分析中,多元变量联合分布建模仍然是一大挑战。当金融资产数量增加时,这一任务变得更加困难。在学术界和实践领域常用的处理方法是使用多元正态分布,但该类模型存在明显的缺陷,多元正态分布不能拟合金融时间序列的尖峰、厚尾和非对称相依结构等特征。另一方面,经济金融因素及其对系统性风险的影响是随着时间推移而不断发展的。例如,金融市场流动性、公司违约风险、经济政策有效性等都随时间和经济状态不同而不同,这些都会对金融资产相依关系产生影响。不考虑这些潜在影响可能会对金融资产相依关系判断不准确,给出错误的政策建议。
次贷危机后学者提出一些新的研究方法,通过降维来估计系统性风险,如CoVaR[1]、MES[2]等方法。这些方法通过单一资产与市场指数关系进行测算,可能会遗漏系统性风险的有用信息,如一个公司可能会对数家公司产生影响,但不会对这个市场指数造成影响,因而这类方法优势有限。Oh和Patton(2016)[3]、Creal和Tsay(2015)[4]、Lucas et al.(2016)[5]等提出的动态因子copula模型,适用于研究多元时间序列动态相依结构变化,在复杂经济条件下评估金融机构(或市场)稳定性,监控系统性风险。
国内对于金融机构系统性风险测度仍集中在单一机构对整体的影响,缺乏对多机构联合的系统性风险研究。随着我国金融改革深化,金融市场一体化程度日益提高,加之金融机构各类综合型业务的开展,使得金融机构间资产负债联系紧密而复杂,金融资产间协动性加强,有必要监测系统性风险动态变化。本文把未定权益分析法和动态因子copula模型结合起来,测度我国金融机构动态系统性风险,为我国监管机构监控系统性风险提供可行参考。
二、文献综述
系统性风险测度一直是金融学者关注和研究的重点内容之一。次贷危机后,金融机构系统性风险监测成为各国金融监管当局的迫切任务。学者提出多种系统性风险测度方法,相关研究主要有以下两个方面:
一是以测度单一金融机构系统性风险贡献为出发点,具体研究方法包括两大类:第一类是假定单一金融机构陷入经营困境,对其他金融机构乃至金融部门的影响,主要有市场指标法[6]、网络模型法[7]、CoVaR方法[1]等;第二类是当金融系统面临危机时,哪些金融机构更易受到影响,损失较大,主要有Shapley值[8]、MES[2]、SRISK[9]等。市场指标法多为实践中金融监管部门使用,金融监管部门可以获得金融机构定期披露的详细信息,但限于信息收集整理时间较长,不利于金融机构系统性风险动态监测和预警。网络模型法面临同样的问题,该方法以金融机构间往来交易数据为基础,更难搜集,多以银行间交易市场数据代替,且无法分析不同金融子行业间风险传导。CoVaR、Shapley值、MES和SRISK方法以金融机构股价数据为基础,时效性较好,便于对金融机构系统性风险实时跟踪监测。
总体而言,这两类方法侧重于分析单一金融机构系统性风险,识别系统重要性金融机构,但不能分析金融机构联合违约带来的系统性风险,不适于整体金融部门系统性风险监测。
二是测度多个金融机构联合违约带来的系统性风险。该类研究主要有未定权益分析法和联合违约概率分析法两大研究方法。未定权益分析法(简称CCA模型)结合了股票价格和资产负债表信息,能获得一系列具有前瞻性且易于计算的公司违约风险指标。学者通过建立国家或部门资产负债表,将CCA模型应用于一国主权债务风险、各宏观部门风险的测度;一些中央银行也开始使用该模型测度金融部门违约风险以及多家金融机构违约可能带来的风险传染,对本国银行业和整个金融部门进行压力测试,如Castren和Kavonius(2009)[10]、Saldías(2013)[11]、Harada et al.(2013)[12]等。Jobst和Gray(2013)提出了Systemic cca分析法,结合极值理论和多元copula产生一个多元极值分布,拟合金融机构间相依结构,捕捉金融系统联合违约的整体预期损失,并用该方法衡量了美国金融体系的系统性风险[13]。未定权益分析法已经应用于分析多家银行、金融部门或主权债务系统性风险,帮助监管部门建立新的监管框架,应对不断提升的系统性风险。联合违约概率分析法是由Segoviano和Goodhart(2009)[14]提出,研究使用当一家金融机构陷于经营困境时,至少一家金融机构也出现经营困境的条件概率密度来衡量系统性风险,将金融机构系统性风险测度由单一维扩展到多维。在此基础上,Zhou(2010)[15]提出用一家特定金融机构出现经营危机时,系统中金融机构陷于经营危机的预期数量衡量系统性风险,给出了系统影响指数和系统脆弱指数两个系统性风险衡量指标。Peeters(2011)[16]使用金融机构规模加权系统影响指数,构建了系统加权损害指数。
这两种方法均测度了金融系统多家金融机构联合违约带来的系统性风险,但在实践应用上仍存在一些问题。CCA分析法主要问题在于个体违约风险指标如何加总为系统性风险指标。目前已有的几种方法为简单算数平均加总、资产加权加总和协方差加总法。这些方法一定程度上反映了金融机构系统性违约风险,但忽略了金融机构间非线性相依结构。Systemic cca分析法使用了非线性相依结构,但模型假定任意两变量间相依结构相同且不随时间变化,这显然与现实不符。联合违约概率方法面临同样问题,在计算金融机构系统性风险指标时需要估计变量联合概率发布,当金融机构数量较多时,固定相依结构假定使得计算结果出现偏差。Oh和Patton(2016)[3]、Lucas et al.(2016)[5]等提出了时变参数的动态因子copula模型,能较好地描述多变量间相依结构的动态变化。本文将CCA模型和动态因子copula模型结合起来,参考联合违约概率方法的系统性风险指标,分析我国金融机构联合违约风险,为系统性风险动态监测提供可行指标。
三、研究设计
(一)未定权益分析法与信用价差计算
未定权益分析法假定资产市场价值随机波动,并服从几何布朗运动,具体形式如下:
dAt=μAAtdt+σAAtdWt
(1)
上式中μA为漂移率或资产收益率;σA为资产收益率的标准差。由伊藤引理可知,At服从对数正态分布。
(2)
公司股权价值可以看作是以资产市场价值为标的,以公司负债为执行价格的欧式看涨期权。给定到期时间T,在风险中性假定下,估计模型时采用同期无风险收益率r代替资产收益率μA,由期权定价公式可得:
Et=AtNd1-De-rT-tNd2
(3)


同时,资产市场价值波动率与股权价值波动率存在如下关系:

(4)
联立式(3)和式(4),优化迭代求解可得At和σA。公司信用风险价值相当于一个以公司资产市场价值为标的,到期债务额为执行价格,到期期限为T-t的欧式看跌期权。如果债权人购买了这样一个期权,那么就可以消除公司违约的信用风险。看跌期权价值可以看作是消除公司债权违约的信用风险成本。进一步的,风险负债价值等于到期债务额的现值减去信用风险成本。
Dt=De-rT-t-Pt
(5)
在风险中性假定下,根据B-S期权定价公式,可得每个公司信用风险成本为:
Pt=De-rT-tN-d2-AtN-d1
(6)
假定债务到期收益率为y,满足y≻r。

(7)
信用价差s=y-r代表债权人所承担违约风险的补偿。代入(5)、(6)和(7)可得:
(8)
由上式可计算出公司信用价差,为监测金融机构违约风险提供了一个明确且易于处理的预警指标。
(二)动态因子copula模型
金融机构违约风险存在明显的动态相关性,基于未定权益分析法计算的信用价差是衡量单个金融机构违约风险的指标,不能反映多个金融机构联合违约风险状况,不利于监管部门监控金融机构系统性风险。使用动态因子copula作为连接函数,拟合金融机构信用价差间动态相依结构,构建系统性风险度量指标,可以有效解决这一难题。
构建高维变量相依结构模型的一个关键问题是降维。学者们提出了一种灵活的因子copula建模框架。结合本文研究内容,考虑如下因子copula模型:
uit=Fxitθ,i=1,2,…,nt=1,2,…,T
xit=λitγλzt+εit,i=1,2,…,n
(9)
z~FZγzεi~iidFεγε
其中,Fxitθ为xit的边际分布函数;zt为变量xit的共同因子;λitγλ为共同因子zt潜在的时变权重;FZγz和Fεγε分别是共同因素和异质因素的单变量分布函数,本文假定FZγz函数形式为Skew-tνz,φz,Fεγε函数形式为tνε。γλ,γZ,γε为所需要估计的copula参数集。
动态模型的一个关键特征是参数如何随时间变化的。学者们针对copula模型提出了多种参数动态化方法,GAS模型在应用于高维动态copula建模时更有优势,它是一种纯粹基于数据本身驱动的时变参数建模方法,一定程度上避免了设定时变参数动态过程的主观性,该方法的详细讨论参见Creal et al.(2013)[17]。这种时变参数建模方法能较好地适应尖峰厚尾型多元变量联合分布概率密度函数,提高了动态波动性和相关性估计的稳定性。因此,本文使用GAS方法描述模型动态特征,动态参数的GAS模型具体形式如下:
logλi,t=ωi+βlogλi,t-1+αsi,t-1,i=1,2,…,n
(10)

上述动态因子copula模型没有具体解析表达式,因此也无法求得该copula模型似然函数解析表达式,只能通过数值方法来解决这一问题。本文使用基于数值逼近的似然函数值最大化方法,估计动态因子copula模型参数值。
(三)系统性风险指标
系统性风险可以定义为大量公司或机构处于经营困境的风险。当其他金融机构处于经营压力之下时,一家金融机构经营出现问题,风险看似可控,实际上却不是这样的。如果一家金融机构处于经营困境中,也许仍然可以获得其他正常金融机构的支持,但当两个、三个或更多金融机构处于经营困境时,情况会变得很糟糕,坏的结果一起发生会使问题变得更严重。本文借鉴相关研究,同时考虑金融机构规模的影响,设计两个指标衡量金融机构系统性风险。
本文定义当金融机构未来一季度信用价差高于某一门限值时,则金融机构处于经营危机中,具体如下:
Yi,t+60=Isi,t+60≻c
(11)
其中,I{}为指示性函数,括号中为真,取值为1,否则取值为0。c为信用价差固定门限值,可根据研究需要设定。
指标一是使用多家金融机构同时出现经营困境的概率衡量系统性风险。联合违约概率定义为:
(12)
其中,wi为根据金融机构规模计算的权重;k为处于经营困境的金融机构数量。
指标二是金融机构i陷入经营困境时,所有金融机构中出现经营危机的比例,称为条件违约概率。定义为:
(13)
四、我国金融机构动态系统性风险测度
(一)数据选择与说明
考虑到数据连续性及研究需要,本文选取在国内A股上市的26家金融机构,包括14家银行、6家证券公司、3家保险公司、3家信托公司,涵盖金融业四个子行业,研究使用日度数据。股权价值等于金融机构总股本(流通A股+非流通股+H股)×当日实际收盘价;采用向前复权股价计算股票收益率,并用GARCH(1,1)测算股权价值波动率;无风险利率选用一年期中央银行定期存款利率;债务违约阀值为短期负债+0.5×长期负债,由于金融机构资产负债表季度公布,本文利用线性插值法转换为日度数据。所有数据均来自于Wind资讯。
样本考察期为2008年1月1日至2016年3月31日,包括了次贷危机爆发影响、财政四万亿投资计划、欧债危机、地方政府债务问题、金融深化改革及经济增速下滑等一系列比较有影响的宏观经济时期,有助于认识复杂宏观经济环境背景对我国金融机构系统性违约风险的影响。
(二)我国金融机构信用价差的动态特征
在分析金融机构系统性风险动态特征之前,首先分析单一金融机构违约风险,本文使用前文介绍的金融机构信用价差这一指标。金融机构信用价差越大,说明其违约损失补偿越高,违约风险越大。将相关变量代入未定权益分析模型,使用MATLAB2012优化求解可得金融机构信用价差。整体来看,信用价差指标能较好地捕捉到单一金融机构违约风险动态变化,反映出不同市场环境和宏观经济背景对金融机构违约风险的影响。
表1列出了样本期内26家金融机构信用价差序列描述性统计分析情况。由表1可以看出各金融机构信用价差序列数值上表现出较大差异,均呈现出尖峰、右偏特征。从均值来看,证券业最高,达到0.227%,然后依次为保险业0.075%、信托业0.056%,银行业最小为0.042%。进一步比较单个金融机构信用价差发现,国有大型商业银行信用价差要显著低于股份制商业银行和城市商业银行,这与陈忠阳和刘志洋(2013)[18]研究一致。这主要是由于大型商业银行的国有属性,其背后有国家信用的支持。市场普遍预期当国有大型商业银行出现偿付问题时,政府会进行救助,存在“大而不能倒”现象,这一预期已经反映到了大型商业银行信用价差中。此外,相比其他金融机构,国有大型商业银行资产规模大、业务范围广、风险控制能力较强等优势,也使其违约风险低于其他金融机构。证券公司违约风险要明显高于其他金融机构。这主要是因为证券公司收益更易受股市波动影响,样本期内几次股市大跌使证券公司收益下降,违约风险较高。

表1 金融机构信用价差描述性统计分析
图1给出了样本考察期内银行业、信托业、保险业和证券业的信用价差动态变化。*限于篇幅,没有给出各个金融机构的信用价差时序图。2008年次贷危机爆发以来,金融机构违约风险不断攀升,至2008年第四季度达到峰值,之后开始回落。2010年第一季度小幅波动之后,基本维持在较低水平。直到2014年底信用价差水平再度提高,2015年一度超过次贷危机期间最高水平。可见,金融机构信用价差易受到市场和经济因素影响,金融机构违约风险短期内可能会剧烈变动。各金融机构信用价差序列动态走势高度一致,样本期内呈现出同升同降的变化,这说明金融机构间违约风险存在动态相关性,表现出较强协动性特征,有必要测度金融机构联合违约风险,加强动态系统性风险监测。

图1 金融机构信用价差动态变化

图2 金融机构因子载荷动态变化
(三)动态因子copula模型估计
由于信用价差数据表现出明显的尖峰和右偏特征,本文首先选用残差服从Stewed-t分布的AR(1)—GARCH(1,1)模型拟合各序列边际分布,然后将估计的标准化残差进行概率积分变换获得uit,用于动态因子copula分析。表2给出了动态因子copula模型估计结果。可以看出,β参数为0.9197,说明模型时变参数具有较高的持久性。时变参数系数比较显著,相比传统静态copula模型,动态因子copula模型具有更好的表现,较好地拟合了金融机构间动态相依结构演变。模型中因子载荷(λt)是序列相关结构的标准指标,因子载荷越大,金融机构间相关性越强[3]。
图2给出了样本期内估计的因子载荷的动态变化。各金融子行业序列为同类金融机构因子载荷的平均值。观察图2我们发现,金融机构间相依结构变动大体可分为三个阶段:2008年1月至2009年12月为第一阶段,2008年因子载荷相对稳定,大部分集中在0.5~1之间,金融机构相关性在0.2~0.5左右;2009年开始在波动中大幅提高到2以上。总体上这一阶段金融机构间相关关系由大到小依次为保险公司、银行、证券公司和信托公司。2010年1月至2014年12月为第二阶段,在此期间因子载荷一直维持在高水平波动,金融机构间相依结构发生明显变化,金融机构相关关系明显提高,达到0.8以上,意味着一家金融机构出现问题,至少还有20家金融机构会同时陷入困境。银行的因子载荷波动较小,且显著小于其他三类公司;保险和证券公司波动较大,一度回落到1.5以下。这一阶段相依关系依次为信托公司、保险公司、证券公司和银行。2015年1月进入第三阶段,金融机构相关性下降,因子载荷降到2以下。证券和信托公司回落到2008年水平,并有进一步下降趋势;银行和保险公司仍然较高,银行降幅最小。这一阶段相关性变为银行最大,保险公司次之,信托和证券公司最小。

表2 动态因子copula模型参数估计结果
注:所有参数均在1%显著性水平上显著。
(四)时变系统性风险测度
比较大的金融危机通常会导致经济萧条或衰退。危机发生时,银行和其他金融机构破产会通过资产负债和流动性渠道触发其他金融机构倒闭,危及实体经济稳定性。最近的金融危机表明传统的微观审慎监管不能有效防范系统性风险。上文研究也证实了金融机构间相依结构会随经济环境变化而不断变动,需要监测系统性风险动态变化。本文利用蒙特卡洛模拟法计算两个系统性风险指标。设定信用价差99%分位数为违约门限值。在时刻t,基于估计的动态因子copula模型产生n组随机变量uit,i=1,…,26t=1,…,n,n为测度周期。因为上市金融机构财务数据季度披露一次,故假定n为60个交易日(约为一个季度),以预测下一季度系统性风险变动状况。然后由边际分布模型迭代求出金融机构下一季度末的信用价差,进而计算出联合违约风险和条件违约概率。重复上述过程1000次,求期望值得模拟的系统性风险。
图3给出了k=2和k=5的联合违约概率动态变化,即同时有2家或5家以上金融机构陷入经营困境的概率。我们发现k=2和k=5时金融机构联合违约概率走势高度一致,k=2时联合违约风险略高于k=5时,说明金融机构间协动性较强。下面以k=2时为例进行分析,2009年第二季度之前金融机构联合违约风险几乎为零,2009年第二季度直接升高到样本期内最大值0.711,这再次表明系统性风险实时监测的必要性。2009年下半年风险概率略有下降但仍在0.68以上。2010年下降到0.6以下,直至2014年第三季度,除2013年第四季度有一个短暂下降外,其他时间均保持在0.5~0.6之间波动。2014年第四季度以来,联合违约风险大幅下降,违约概率回落到0.1以下。2016年有上升趋势,但上升幅度较小。
图4给出了条件违约概率动态变化。可以看出同联合违约风险表现相似,2009年第二季度条件违约概率攀升至0.84以上,第三季度达到极值1,这表明任何一家金融机构违约时,其他金融机构也会一起违约。2009年底重新下降到0.85左右,一直维持到2014年第三季度。2014年底下降到0.1以下,之后2016年又有所上升超过0.7。当一家金融机构条件违约概率较低时,说明金融机构间相关性较低。这家金融机构经营陷入困境不会导致其他金融机构经营出现问题。如果金融机构条件违约概率高于其他金融机构,说明其对于金融市场稳定有较强影响力,是系统重要性金融机构,在样本期间内,四类金融机构表现差异不大,大部分时间段相差不超过2%,金融机构间表现出较强相关性,与上文因子载荷分析结论相一致。
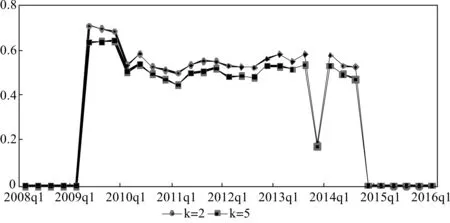
图3 金融机构联合违约概率动态变化
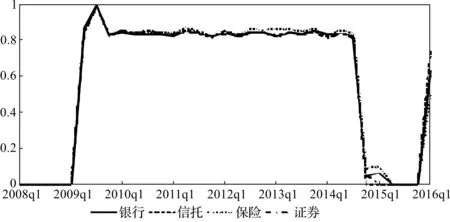
图4 金融机构条件违约概率动态变化
综合对比以上分析,我们发现2008年次贷危机爆发期间,单一金融机构违约风险显著提高,这与现有研究一致;与二元模型(MES、CoVaR等)测度结果不同,次贷危机期间系统性风险并不高,而是2009年下半年开始达到较高水平。二元模型仅考虑了单个金融机构股价指数与市场指数关系,没有涉及金融机构间相依关系。本文使用的动态因子copula模型能拟合金融机构间相依结构,并且较好地描述了动态相依结构的变化,对系统性风险评估更准确可靠。次贷危机对我国影响主要有金融和贸易两个渠道。我国金融机构参与国际金融市场交易规模有限,次贷危机爆发主要是国内投资者信心和市场预期受到冲击,股市下跌造成金融机构资产市场价值下降,进而单个金融机构融资成本上升违约风险较高。危机发生并未造成我国金融机构资产大规模减记,金融渠道影响较快但影响有限。近年来,出口贸易是拉动经济增长的重要源动力之一。次贷危机发生导致我国出口负增长,不少企业因此陷入经营困境,甚至破产跑路,这直接影响到金融机构投资或贷款的收回,给金融机构造成较大损失。这一渠道作用较慢,直到2009年才逐渐显现,但影响较大,金融机构受波及范围较广。因此,次贷危机后金融机构间相关性大大提高,远超过次贷危机期间水平。另一方面,为稳定经济增长,2008年底政府推出了扩大内需、促进经济增长的十项措施,预计到2010年底投资四万亿。各金融机构纷纷通过影子银行等方式为政府投资融通资金,这使得金融机构间本已紧密的资产负债联系更加错综复杂,协动性增强,出现“一荣俱荣、一损俱损”的局面。金融机构被动成为一个整体,这一情况直到2014年底才有所缓解。从系统性风险测度结果来看,2014年底以来,金融机构系统性违约风险回落,这主要缘于金融机构相关性减弱而非其自身风险的下降。政府在充分认识经济进入新常态阶段后,实施“一带一路”“供给侧改革”等经济发展战略,不断深化金融体制改革,加强金融机构违约风险监控,增强金融机构抗风险能力,2014年底以来多次下调法定存款准备金比率,释放流动性。在一系列经济金融政策措施作用下,金融机构相关性下降,虽然在金融监管压力下,单一金融机构违约风险有所提高,但金融业整体系统性风险大大降低。
五、结 论
本文基于2008年1月1日至2016年3月31日股价和财务数据,运用未定权益分析法测度我国26家上市金融机构的信用价差,并构建动态因子copula模型估计金融机构系统性风险。研究发现信用价差变动较好地揭示了单个金融机构违约风险动态变化特征;相比二元变量模型,动态因子copula模型表现更好,描述了样本期内金融机构间相依结构变化。
从单一金融机构违约风险来看,次贷危机期间和2015年以来金融机构个体违约风险均大幅提高,远超过其他时间段违约水平。从金融机构系统性违约风险来看,与单一金融机构违约风险相反,上述两个时间段系统性违约风险较小,不到0.1,而2009年下半年到2014年底,联合违约风险指标一直在0.8以上,这主要是缘于这段时期金融机构较高的相关性。这一发现与二元变量模型结果明显不同,说明仅关注二元变量相依关系不足以反映金融业整体风险状况,必须加强对多家金融机构间相依结构变动的关注。正如前文所言,一家金融机构违约对金融市场影响可能有限,但当其他金融机构与这家金融机构协动性较强,也同时陷入困境时,将对金融市场造成严重影响,二元模型无法揭示这一点。本文分析认为由于我国金融机构开放度较低,受次贷危机直接影响较小,主要问题来自于出口负增长带来经济下滑,企业破产倒闭造成各种呆坏账,这是2009年之后金融机构相依关系变强、系统性风险加大的主要原因。
从本文分析结果来看,各金融机构违约风险呈现较大差异,相比其他金融机构,银行违约风险较低,但其相依关系波动较小,近期处于高点,需加强监控。传统微观审慎监管措施不能有效防范系统性风险,单一金融机构违约风险低,系统性风险不一定低,系统性风险更多地依赖于金融机构间相依结构。从系统性重要机构来看,由于相关性较高,条件违约概率测度结果没有显著差异,表明在一家金融机构陷入困境时,其他金融机构以一个较大的概率陷入经营困境,没有发现明显的系统性重要机构,或者说每个金融机构都很重要。这意味着金融监管部门仅关注系统性重要机构仍然不足。因此,需要加强宏观审慎监管,关注金融机构间相依结构变化。
[1] Adrian,Tobias,Markus K. Brunnermeier.CoVaR[R].National Bureau of Economic Research,2011.
[2] Acharya, V.,R. F. Engle,M. Richardson.Capital Shortfall: A New Approach to Ranking and Regulating Systemic Risks[J]. American Economic Review,2012,102(3),pp.59-64.
[3] Dong Hwan Oh,Patton A. J. Time-Varying Systemic Risk: Evidence from a Dynamic Copula Model of CDS Spreads[J].Journal of Business and Economic Statistics,2016,Forthcoming.
[4] Creal D. D.,Tsay R. S.High Dimensional Dynamic Stochastic Copula Models[J].Journal of Econometrics,2015,189(2),pp.335-345.
[5] Lucas A.,Schwaab B.,Zhang X.Modeling Financial Sector Joint Tail Risk in the Euro Area[J].Journal of Applied Econometrics,2016,Forthcoming.
[6] Financial Stability Board.Policy Measures to Address Systemically Important Financial Institutions[R]. 2011.
[7] Mistrulli,Paolo Emilio.Assessing Financial Contagion in the Interbank Market: Maximum Entropy Versus Observed Interbank Lending Patterns[J].Journal of Banking and Finance,2011,35(5),pp.1114-1127.
[8] Tarashev N.,Borio C.,Tsatsaronis K.The Systemic Importance of Financial Institutions[J].Bis Quarterly Review,2009,pp.75-87.
[9] Brownlees, T.C.,Engle, R.F.Volatility, Correlation and Tails for Systemic Risk Measurement [Z].NYU-Stern Working Paper,2012.
[10] Castren, O.,Kavonius, I. K. Balance Sheet Interlinkages and Macro-Financial Risk Analysis in the Euro Area[Z].ECB Working Paper,No.1124,2009.
[11] Saldías M.Systemic Risk Analysis Using Forward-looking Distance-to-Default Series [J].Journal of Financial Stability,2013,9(4),pp.498-517.
[12] Harada K.,Ito T.,Takahashi S.Is the Distance to Default A Good Measure in Predicting Bank Failures? A Case Study of Japanese Major Banks[J].Japan & the World Economy,2013,27(4), pp.70-82.
[13] Jobst A.,Gray D. F.Systemic Contingent Claims Analysis—Estimating Market-Implied Systemic Risk[Z].IMF Working Paper,No.13(54),2013.
[14] Segoviano Basurto M.,Goodhart C.Banking Stability Measures[J].Journal of Information Processing,2009,23(2),pp.202-209.
[15] Zhou C.Are Banks Too Big to Fail? Measuring Systemic Importance of Financial Institutions [J].International Journal of Central Banking,2010(12),pp.205-250.
[16] Peeters,R.Quantifying Systemic Importance:An Extreme Value Approach[D].Master Thesis, Maastricht University,2011.
[17] Creal,D.D.,S.J. Koopman,A. Lucas.Generalized Autoregressive Score Models with Applications[J].Journal of Applied Econometrics,2013,28(5),pp.777-795.
[18] 陈忠阳,刘志洋.国有大型商业银行系统性风险贡献度真的高吗?——来自中国上市商业银行股票收益率的证据[J].财贸经济,2013,(9):57-66.
DynamicMonitoringofSystematicRiskofChinaFinancialInstitutions——BasedonCCAandDynamicFactorCopulaModel
WANG Peihui,YUAN Wei
(School of Economics,Hebei University,Baoding 071002,China)
This paper uses contingent claim analysis and dynamic factor copula model to study the systematic risk of financial institutions from January 2008 to March 2016.The findings are as follows: (1) The credit spread reveals the dynamic changes of the single financial institution’s default risk, which was at a high level during the subprime crisis and has risen again since 2015. The risk was at its highest in securities companies, followed by insurance companies,and trust companies,and at its lwest in banks. (2) Simulation of the systematic risk index reflects the systematic risk of financial institutions. During the second half of 2009 to the end of 2014 the systematic risk was at its highest. It is found that the higher risk of default in a single financial institution does not mean that the systematic risk is high, which depends on the dependence structure of financial institutions. Therefore, when strengthening the macro prudential supervision, regulators should pay attention to the dynamic changes in the dependence structure.
Systematic Risk; Contingent Claim Analysis; Dynamic Factor Copula Model
2016-12-23
国家社科基金青年项目(14CJY073)
王培辉(1981-),男,河北沧县人,河北大学经济学院副教授;袁薇(1982-),女,河北邯郸人,河北大学经济学院讲师。
F832
A
1004-4892(2017)12-0043-11
(责任编辑:原蕴)
