一种复杂条件下编队姿态协同控制方法

彭司萍, 龙正平, 马 肸

(火箭军工程大学理学院，西安 710025)

一种复杂条件下编队姿态协同控制方法

彭司萍, 龙正平, 马 肸

(火箭军工程大学理学院，西安 710025)

针对无角速度量测及饱和输入条件下的编队姿态协同控制问题，将未知饱和控制影响与外部扰动合并为复合外部扰动，设计了一种外部状态观测器准确估计系统角速度和复合外部扰动；在此基础上，提出了一种有限时间滑模协同控制律，通过构造合适的Lyapunov函数从理论上证明了系统的稳定性；仿真结果表明，该方法能够在有限时间内实现对姿态的准确估计和协同控制。

编队协同； 航天飞行器； 状态观测器； 外部扰动； 饱和输入； 滑模控制

0 引言

编队飞行由于在军事侦察、深空探测、环境监测和定位服务等领域的巨大优势和广阔前景而引起专家和学者的高度重视[1-5]。与单个飞行器相比，编队协同控制不仅需要在局部连通条件下保证编队实现队形、姿态协同控制[6]，而且需要克服外部扰动、控制饱和、通信时延和模型不确定性等因素的影响[7]，这就使得控制律设计变得异常复杂。因此，在复杂条件下，如何设计高精度和强鲁棒性的协同控制律仍然是当前编队协同控制研究的重点和难点问题[8-12]。

从公开文献来看，针对单个飞行器无角速度量测条件下的控制律设计已经比较成熟。文献[13]利用刚体被动特性，设计了基于姿态误差四元数的非线性滤波器作为反馈输入，从而消除角速度量测的必要性；文献[14]采用线性渐近稳定的姿态控制器，利用欧拉参数描述被动刚体，但无法避免姿态奇异的问题；文献[15]在文献[14]的基础上提出了非奇异四元数的自适应全状态反馈控制器，并保证系统的全局渐近稳定性；文献[16]则采用修正罗德里格斯参数描述飞行器姿控方程，设计了无源滤波器实现对飞行器姿态的跟踪，但是只能保证有限时间内实现系统姿态精确估计，并没有设计控制律保证飞行器姿态实现有限时间精确跟踪。现有关于编队姿态协同控制的研究多是假定姿态和角速度已知的全姿态反馈控制律设计，文献[17-19]利用全状态反馈解决了编队姿态协同控制问题，即编队成员及其相邻成员的姿态及角速度信息均可量测，从而构成全状态反馈控制器的设计。从现有文献来看，尚未有关于同时考虑无角速度量测和饱和输入条件的编队姿态有限时间协同控制的研究。

1 数学模型

飞行器的姿控系统可被认为是刚体系统。为了避免姿控中存在的奇异问题，通常采用修正罗德里格斯参数(MRPs)描述刚体姿态运动。飞行器的姿态运动学和动力学方程表示为[20]

(1)

式中：n为编队成员个数；Ji∈R3×3代表第i个飞行器的转动惯量矩阵；ui∈R3为控制力矩；di∈R3为外部扰动力矩；ωi∈R3为本体坐标系B下第i个飞行器的角速度；qi∈R3表示描述飞行器姿态的修正罗德里格斯参数[21]。

式(1)飞行器姿控系统可以转化为

(2)

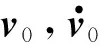
2 一致性问题和有限时间观测器

2.1 一致性问题

所谓一致性问题是指随着时间的演化，编队系统中所有成员的状态趋于一致。一致性协议(Consensus Protocol)是系统成员之间相互作用的规则，它描述了每个成员与它相邻成员间的信息交换过程。

在一致性问题的研究中，图论是重要的分析工具，在此对本文中涉及的部分图论概念进行简单介绍。图由顶点和边组成，记为G=(V,E,A)，其中，边缘集E(G)⊆V×V={(vi,vj),i,j=1,…,n}，集合V={v1,v2，…,vn},A=(aij)∈Rn×n为加权的邻接矩阵,在图中假设节点与自身没有连通性，即aii=0，另外，若节点vj有一条边指向节点vi，则aij=1，否则，aij=0。如果aij=aji，对所有的i,j∈V均成立，则系统为无向图，否则为有向图。

2.2 有限时间状态观测器

为了能够处理未知状态的影响，可行的办法是通过设计有效状态观测器实时估计未知状态真实值。扩张状态观测器(ESO)是一种有效的非线性系统观测器[22]，可以将系统扰动作为系统状态估计出来。为此，本文设计一种新型的扩张观测器以实现未知状态的有限时间观测

(3)

3 主要结论

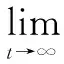
3.1 姿态追踪误差系统

为了便于分析，引入两类状态辅助变量：绝对状态误差和相对状态误差。其中，绝对状态误差为

将其代入式(2)的姿控系统得到姿态追踪误差系统

(4)

定义相对状态误差

(5)

同时，定义耦合追踪误差αi1,αi 2,αi 3∈R3为

式中：ai j是邻接权重矩阵A的元素，若记M=(L+B)⊗I3，则耦合追踪误差可转化成

故可得到如下姿控方程

(6)

3.2 滑模协同控制律设计

首先引入滑模控制变量si=δαi1+αi 2，其中,δ为给定的正整数。对si两边求导可得

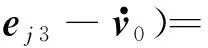
(7)

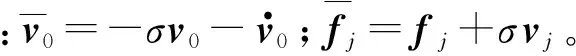
对于第i个飞行器，提出如下滑模控制律

(8)

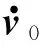
3.3 稳定性分析

式(8)的控制律稳定性可由如下定理得到。

定理1考虑式(3)非线性观测器，当系统存在外部扰动且角速度不可量测时，式(8)的控制律能够保证姿态追踪误差在有限时间内收敛到稳定点附近。

证明给定Lyapunov函数

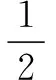
(9)

对Lyapunov函数两侧求导，并将式(6)和式(8)代入式(9)即可得到

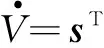
(10)

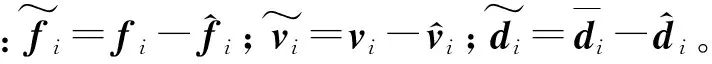
(11)

式中:c1=2λminkmin;c2=nε。

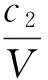
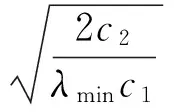
(12)

进而得到，绝对姿态追踪误差e1可以在有限时间内收敛到

(13)

综上所述，式(8)的控制律能够保证编队飞行器在有限时间内跟踪期望的姿态轨迹q0，且保证绝对姿态跟踪误差e1在有限范围内。

3.4 饱和控制条件下的滑模协同控制律设计

在实际工程中，饱和控制是控制律设计中一项非常重要的非线性约束。本文主要考虑式(1)编队姿控系统在角速度不可量测以及未知非对称饱和控制条件下的姿态协同控制问题。

假定未知非对称饱和控制ui有如下形式

(14)

式中：νri k为控制输入，k=1,2,3；umin i和umax i为未知饱和控制上下界参数，且umin i≠umax i代表非对称控制输入。

为了便于分析，将式(1)的系统转换为

(15)

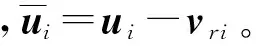
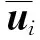
(16)

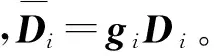
基于式(3)的观测器输出，提出饱和控制条件下的控制律为

(17)

则式(15)的编队飞行器姿控系统稳定性可由定理2给出。

定理2考虑姿态追踪系统存在角速度不可量测，饱和控制和外部扰动条件下，观测器设计如式(3)所示，则在式(17)的控制律作用下，绝对姿态追踪误差e1在有限时间内收敛到平衡点附近。

证明与定理1证明类似，此处从略。

从式(15)可以看出，虽然饱和控制的上下界未知，但是通过转化可将控制输入未知项与外界扰动合并，由所设计的观测器估计得到真实值，进而通过控制律补偿最终消除未知饱和控制项的影响。

4 数值仿真

给出一个仿真算例，以此验证所设计控制算法的有效性。

设计方案如下：假定飞行器编队由6个Follower飞行器和1个Visual Leader飞行器组成，编队成员之间的通信拓扑关系如图1所示。其中,只有成员1,6能够获得期望的姿态信息。

图1 编队飞行器通信拓扑示意图Fig.1 Communication topology of formation

设加权邻接矩阵A和B分别为

B=diag(0.1,0,0,0,0,0.1)。

将飞行器视为刚体，转动惯量矩阵采用文献[21]提供的数值

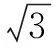
图2a、图2b分别表示观测器的角速度、姿态观测误差随时间的变化曲线，从图中可看出，所设计的观测器大约在2 s之内即可实现对真实角速度和姿态的精确跟踪。图3表示编队成员姿态随时间的变化曲线，从图中可以看出，在控制器的作用下，编队成员的姿态能够在有限时间内实现对期望状态的跟踪。根据图4容易看出，所设计的滑模面能够在较短时间内收敛到平衡点附近。

图2 姿态观测误差随时间变化曲线Fig.2 Observation error versus time

图3 编队成员姿态随时间变化曲线Fig.3 Attitude of formation members versus time

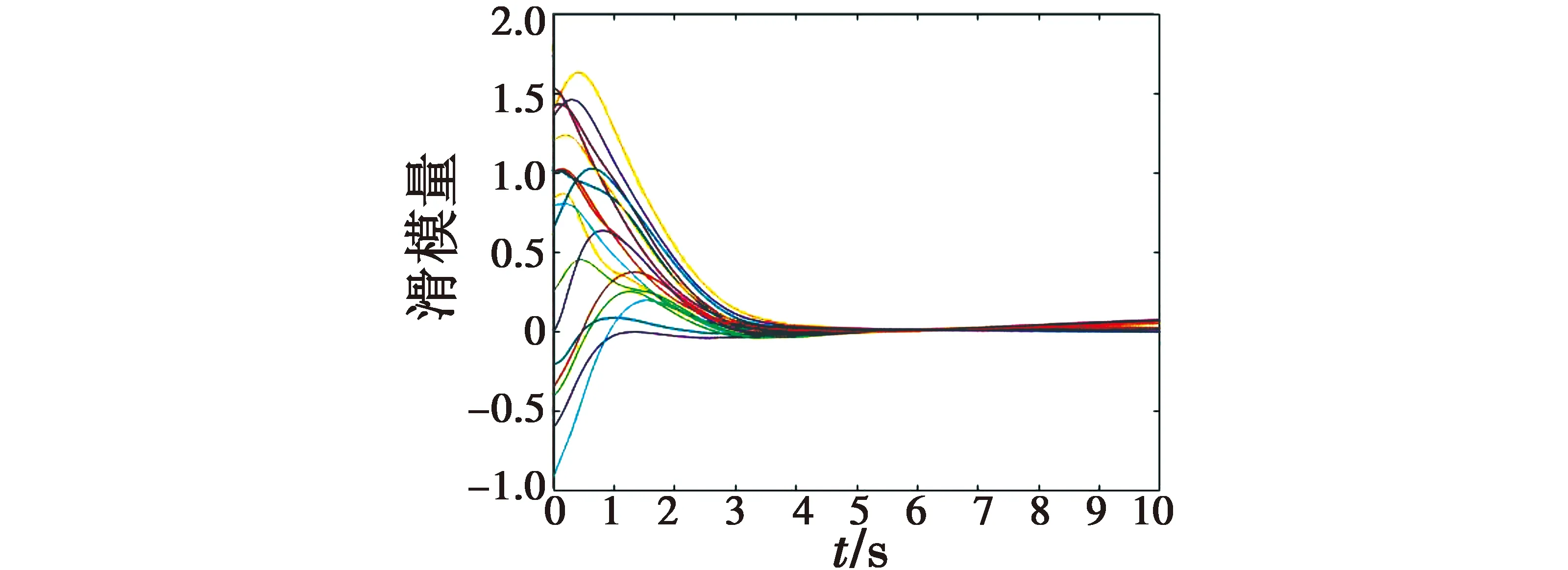
图4 滑模面随时间变化曲线Fig.4 Sliding mode surface versus time

5 结论

本文研究了角速度不可量测、存在饱和控制及外部扰动条件下的编队飞行器姿态协同控制问题。针对角速度不可量测问题，设计了有限时间观测器，实现对飞行器角速度的有限时间估计；将饱和控制的约束与外部扰动合并转化为一个复合外部扰动；提出基于观测器输出的有限时间滑模协同控制律，保证飞行器姿态追踪误差在有限时间内收敛到稳定状态；通过构建合适的Lyapunov函数，从理论上证明了所设计控制算法的有效性。下一步，将考虑切换拓扑、通信时延等条件下的姿态协同控制问题。

[1] 吴婧馨.编队卫星分布式姿态协同控制研究[D].哈尔滨:哈尔滨工业大学,2012.

[2] 丁世宏,李世华.空间飞行器姿态的有限时间跟踪控制方法[J].航空学报,2007,28(3):628-633.

[3] 陈天立,周超,周绍磊,等.面向协同突防的无人飞行器自动编队控制[J].电光与控制,2014,21(5):58-62.

[4] DU H,LI S.Finite-time attitude stabilization for a spacecraft using homogeneous method[J].Journal of Guidance, Control,and Dynamics,2012,35(3):740-748.

[5] 赵刚,周琳莉,黄席樾.六自由度飞行器编队建模与控制[J].系统仿真学报,2011,23(10):2178-2183.

[6] 邵义龙,段欣妤.多无人飞行器协同编队控制[J].科技信息,2013(20):111-112.

[7] KANG W.NonlinearHcontrol and its application to rigid spacecraft[J].IEEE Transactions on Automatic Control,1995,40(7):1281-1285.

[8] FRAGOPOULOS D,INNOCENTI M.Stability considerations in quaternion attitude control using discontinuous Lyapunov functions[J].IEE Proceedings-Control Theory and Applications,2004,151(3):253-258.

[9] JOSHI S M,KELKAR A G,WEN J T Y.Robust attitude stabilization of spacecraft using nonlinear quaternion feedback[J].IEEE Transactions on Automatic Control,1995, 40(10):1800-1803.

[10] KRSTIC M,TSIOTRAS P.Inverse optimal stabilization of a rigid spacecraft[J].IEEE Transactions on Automatic Control,1999,44(5):1042-1049.

[11] PARK Y.Robust and optimal attitude stabilization of space-

craft with external disturbances[J].Aerospace Science and Technology,2005,9(3):253-259.

[12] TSIOTRAS P.Stabilization and optimality results for the attitude control problem[J].Journal of Guidance, Control,and Dynamics,1996,19(4):772-779.

[13] LIZARRALDE F,WEN J T.Attitude control without angular velocity measurement:a passivity approach[J].IEEE Transactions on Automatic Control,1996,41(3):468-472.

[14] TSIOTRAS P.Further passivity results for the attitude control problem[J].IEEE Transactions on Automatic Control, 1998,43(11):1597-1600.

[15] TAYEBI A.Unit quaternion-based output feedback for the attitude tracking problem[J].IEEE Transactions on Automatic Control,2008,53(6):1516-1520.

[16] AKELLA M R.Rigid body attitude tracking without angular velocity feedback[J].Systems & Control Letters,2001,42(4):321-326.

[17] 李贵明,刘良栋.刚体卫星姿态的有限时间控制[J].空间控制技术与应用,2011,37(3):1-8.

[18] DIMAROGONAS D V,PANAGIOTIS T,KOSTAS J.Leader-follower cooperative attitude control of multiple rigid bodies[J].Systems & Control Letters,2009,28(6):429-435.

[19] CHUNG S J,AHSUN U,SLOTINE J E.Application of synchronization to formation flying spacecraft:Lagrangian approach[J].Journal of Guidance,Control,and Dynamics, 2009,32(2):512-526.

[20] 张松,万晓正,贾鹤鸣,等.基于模糊自适应终端滑模的飞行器姿态跟踪控制[J].自动化技术与应用,2014,33(7):1-7.

[21] ZOU A M.Finite-time output feedback attitude tracking control for rigid spacecraft[J].IEEE Transactions on Control Systems Technology,2014,22(1):338-345.

[22] 曹伟.基于终端滑模的飞行器姿态有限时间控制研究[D].秦皇岛:东北大学,2012.

CoordinatedAttitudeControlforSpacecraftFormationFlyingUnderComplicatedCondition

PENG Si-ping, LONG Zheng-ping, MA Xi

(College of Science,Rocket Force University of Engineering,Xi’an 710025,China)

This paper focuses on the attitude tracking control problem of spacecraft formation flying under unmeasured angular velocity and saturation input.By combining the unknown saturation effect with the external disturbance into a compounded disturbance,a novel finite-time observer was designed to estimate the angular velocity and compounded disturbance.Based on which,a finite-time sliding-mode cooperative control protocol was proposed.The stability of the system was verified theoretically by constructing an appropriate Lyapunov function.Simulation result shows that the method can implement accurate estimation and cooperative control to the attitude in limited time.

formation coordination; spacecraft; state observer; external disturbance; input saturation; sliding mode control

V448.2

A

1671-637X(2017)03-0046-05

2016-02-06

2016-04-16

彭司萍(1979 —),女，湖南保靖人，硕士，讲师,研究方向为军事运筹学。