GPS/北斗组合卫星导航系统快速选星算法

刘 帅， 赵国荣， 高 超， 曾 宾

(海军航空工程学院,a.研究生管理大队； b.控制工程系，山东 烟台 264001)

GPS/北斗组合卫星导航系统快速选星算法

刘 帅a， 赵国荣b， 高 超b， 曾 宾b

(海军航空工程学院,a.研究生管理大队； b.控制工程系，山东 烟台 264001)

为实现GPS/北斗组合卫星导航系统的快速选星，提出一种基于几何布局的快速选星算法。根据最优选星方案的卫星分布特点，利用卫星高度角和方位角信息实现卫星的区域划分，应用代价函数法对中仰角区域的卫星进行筛选，得到最终的选星方案。与最优选星算法相比，该算法计算量明显减小；仿真结果表明，该算法能将几何精度因子(GDOP)控制在小于2.5的范围内，具有较好的选星效果。综合考虑算法复杂度和选星效果，基于几何分布的快速选星算法能够满足航空航天等对精度和实时性要求较高的领域的需求。

组合导航； 选星算法； 几何布局； 代价函数； 北斗导航系统

0 引言

全球卫星导航系统(GNSS)具有全球、全天候、连续、实时的精密三维导航与定位能力，被广泛应用于定位、测量、授时等各个领域[1]。截止2012年，GPS系统已拥有31颗在轨卫星，成为全球星座组网最完善、用户数量最多的卫星导航系统[2]。同时，GLONASS，Galileo和北斗系统的快速发展使得卫星导航领域具备了更多的活力与潜力。多个卫星导航系统，可以增加可见星的数量，为用户提供更多可利用的数据，从而为提高卫星导航精度和系统的稳定性创造了条件。但可见星数目的增加，不可避免地造成不同系统间数据的冗余，因而对接收机的数据处理能力和处理速度提出了更高的要求。在航空航天等领域，卫星导航系统往往被应用于动态定位、快速姿态测量等实时性要求较高的方面，此时，提高运算速度是非常重要的。

传统的选星算法运算量大，难以满足航空航天对实时性要求较高的需求。本文从导航卫星选取的角度研究如何充分利用多个卫星导航系统的有用信息，同时避免多卫星导航系统带来的冗余，以期提高组合卫星导航系统的效率和精度。

1 基本概念

卫星选星主要是指从接收机能够接收到的所有可见星中选取一部分空间分布合理、导航解算效率高、效果好的卫星作为信号来源，用于定位、定姿等具体应用。

1.1 几何精度因子(GDOP)

在卫星导航领域，卫星导航定位误差的标准偏差σG可以表示为

σG=GGDOP·σUERE

(1)

式中,σUERE表示伪距测量值的标准偏差。从式(1)不难发现，几何精度因子是影响导航定位精度的重要参数，在伪距测量值标准差确定的情况下，其值越小，导航定位精度越高。研究选星算法的目的，就是要在较小的计算复杂度下得到较高的导航定位精度，因此，GDOP可以用来作为衡量选星算法性能优劣的重要指标。

GDOP可以做如下定义

(2)

式中,G为观测矩阵，假设共有N颗可见星，则G可以写成下列形式

(3)

式中，Ii(i=1,2,…,N)表示第i颗卫星相对于接收机位置的单位观测矢量。

1.2 最优选星的几何分布

卫星的空间几何分布对导航精度有着重要的影响，通过对最优选星方案的卫星几何分布进行研究，可以得出一些可供借鉴的有用信息。文献[5]的研究成果表明，当卫星较为分散地分布于接收机的不同侧时效果最好。文献[6]通过研究大量的实测数据，提出了一种GDOP值相对较小的卫星分布：一定数量的可见星处于接收机天顶位置,其他可见卫星均匀地分布在低仰角圆面附近。表1给出了不同选星数下处于天顶位置的卫星数目及相应的GDOP值。

文献[7]对GDOP与可见星方位角和仰角的关系进行了研究，通过仿真发现，被排除的卫星均处于30°～60°仰角范围内，且有一个或多个方位角邻近的其他卫星。结合这个结论，文献[7]提出一种基于被排除卫星分布规律和高低仰角区卫星数目比的选星算法，仿真结果显示其具有较好的选星效果。

表1 选星总数与天顶位置卫星数关系

1.3 代价函数

在卫星导航定位中，可能会出现几颗卫星与接收机连线几乎在一条线上的情况，此时它们提供的信息将存在很大的冗余。为提高效率，在选星过程中应尽量避免这种情况。通过两颗卫星视线向量的相似性来去除冗余卫星是一种有效的方法[8]。

假设接收机观测两颗卫星i和j的视线向量的夹角为θij，则代价函数定义为

Jij=cosθij。

(4)

不难发现，两条视线向量的夹角越小，即两视线向量越接近于共线，则代价函数值越大，可以用代价函数来反映两条视线向量的共线程度。

为了计算Jij，定义矩阵

(5)

式中,Ii(i=1,2,…,N)含义同式(3)。

通过矩阵F可以计算得到矩阵

(6)

进而，可以得到

(7)

通过求矩阵D中的最大元素，可得到相互间“冗余”最大的两颗卫星，进而可以从二者中排除一颗。

在排除卫星的过程中，可以借鉴文献[6]的结论：当高、低仰角区卫星数目比k1∶k2<1∶3时，选择仰角高的卫星而排除仰角低的卫星；反之，当高、低仰角区卫星数目比k1∶k2>1∶3时，选择仰角低的卫星而排除仰角高的卫星。

2 基于空间分布的快速选星算法

从卫星空间几何分布的角度入手，综合考虑高度角、方位角两方面因素，并与代价函数法结合，本文提出一种综合快速选星算法，具体步骤如下所述。

1) 根据仰角大小，将空间划分为3个区域，低仰角区(0°～30°)、中仰角区(30°～60°)和高仰角区(60°～90°)。假设预期的选星数为k，根据表1中的数据确定选择的高仰角区卫星数目k1。

2) 计算低仰角区的卫星个数k2。若k≤k1+k2，则从低仰角区删除k1+k2-k颗卫星，余下的低仰角星与高仰角区选出高度角最大的k1颗卫星共同构成选星方案。若k>k1+k2，用代价函数法在中仰角区删除N-k颗卫星。在具体操作时，可以按照均匀分布的原则，根据方位角将中仰角区划分为m部分，且每一部分包含左边界不包含右边界。根据k1和k2的比例关系，在每一部分中，用代价函数法对可见星进行逐步筛选，直到余下的卫星数满足要求。具体的选择过程如图1所述。

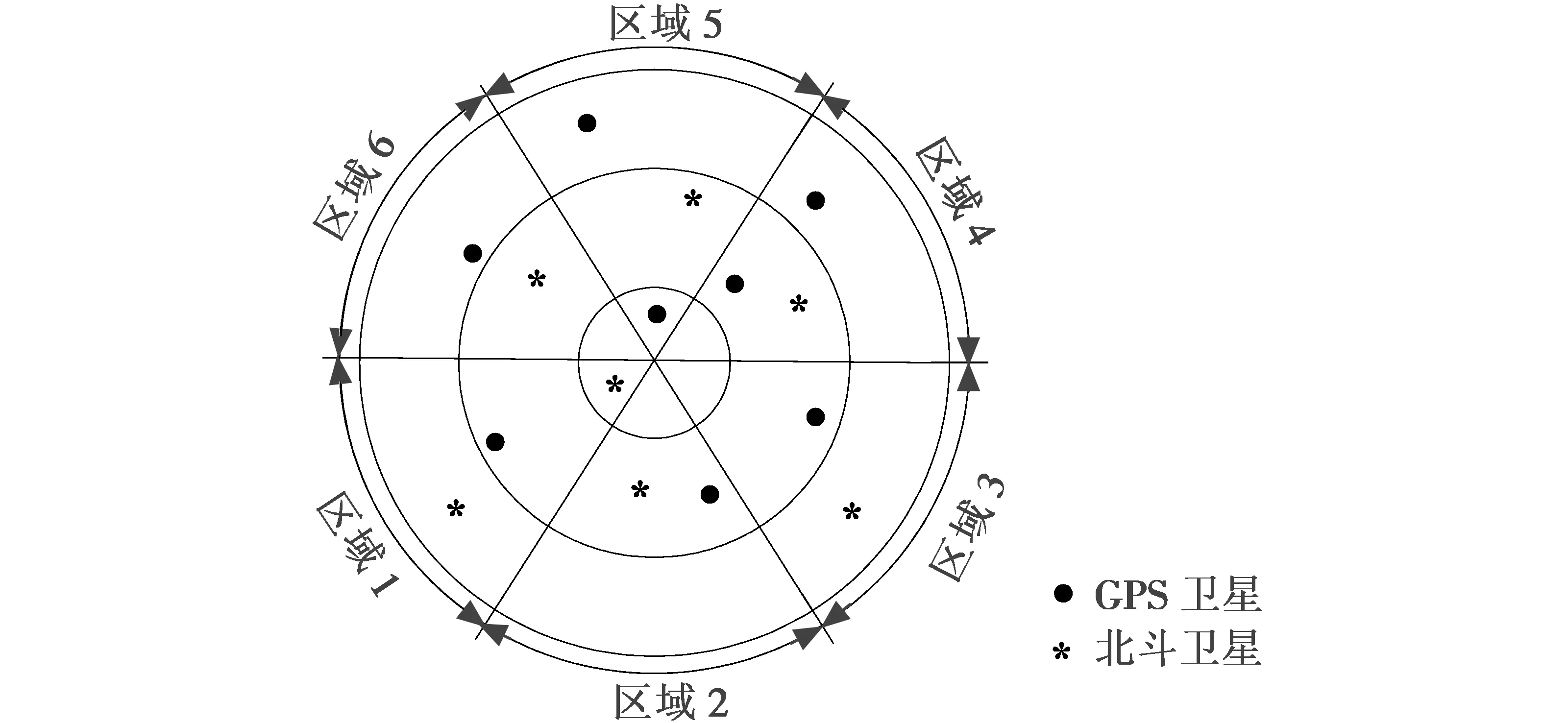
图1 区域划分示意图Fig.1 Schematic diagram of group division

算法的流程如图2所示。

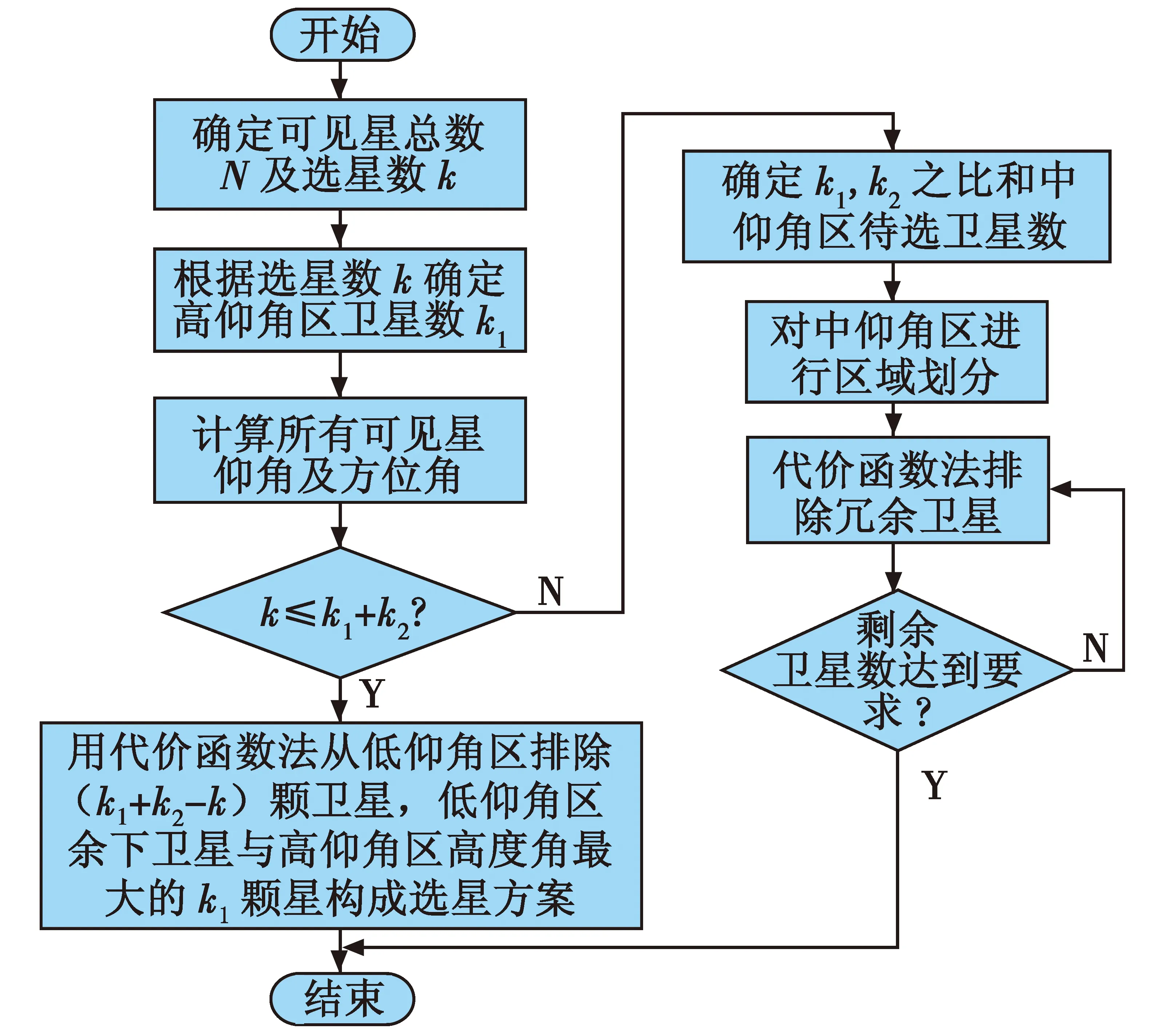
图2 选星算法流程图Fig.2 Flow chart ot the fast satellite selection algorithm

3 仿真及结果分析

多个卫星导航系统使得空间中可见星数量大大增加，现有的GNSS接收机一般都能够同时接收多个卫星导航系统的信号，使得卫星在导航定位过程中有了更多的选择余地。首先，对多个卫星导航系统下的可见星数目进行仿真[9]，以北纬37.52°，东经121.39°，高度15 m处的GPS/北斗双系统接收机为例，得到图3所示的可见星数目仿真图。

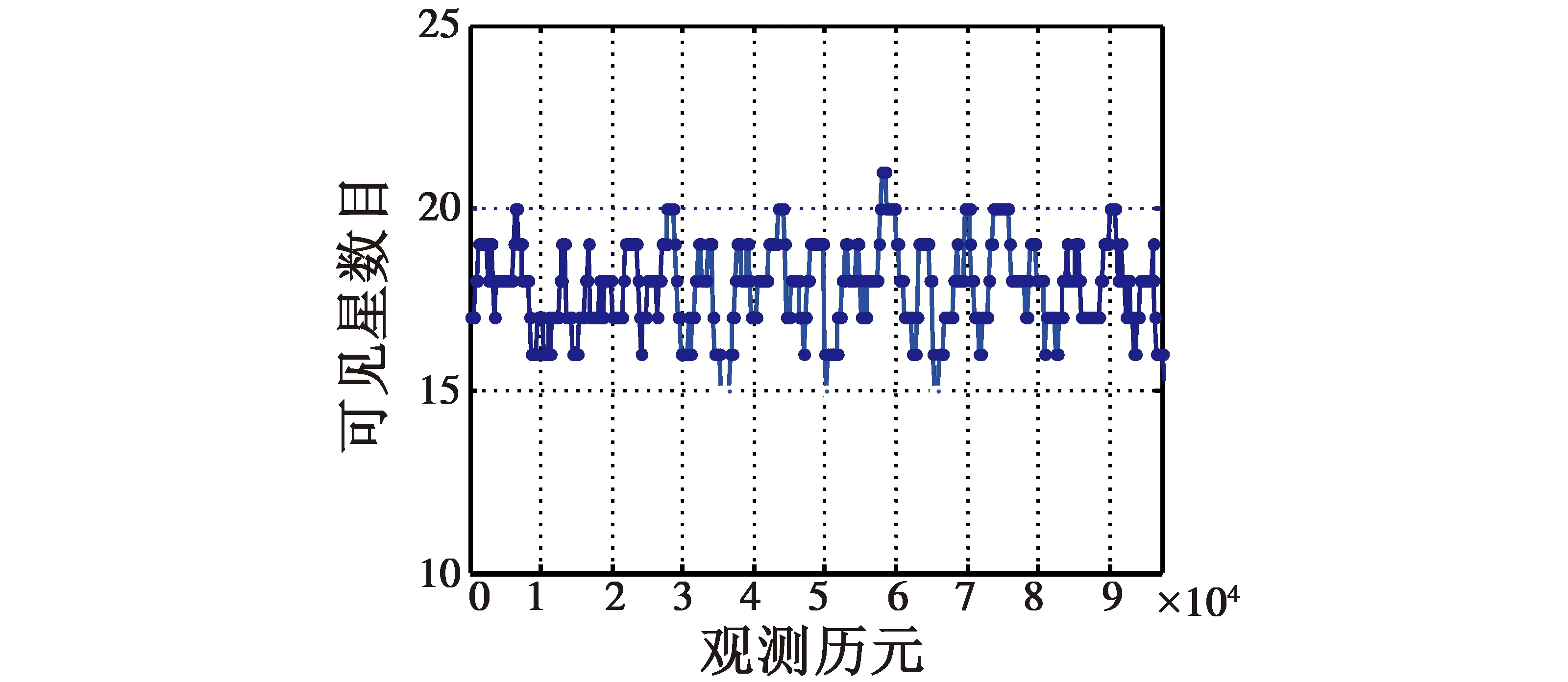
图3 可见星数目仿真图Fig.3 The number of visible satellites

从图3中不难看出，双系统接收机可以接收到的可见星数目在15颗到21颗之间。可见星数量的增多使得导航定位更加准确可靠，但也不可避免地带来了计算量的增加。表2从计算量的角度对最优选星算法和本文提出的快速选星算法进行了对比。

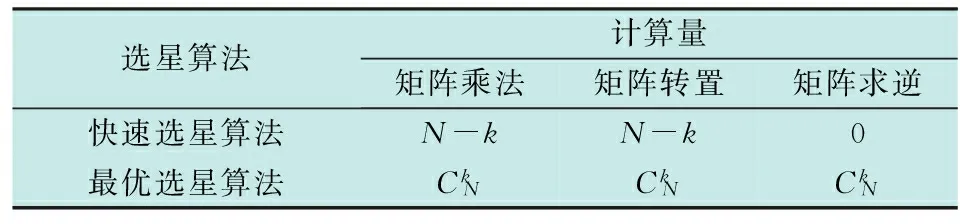
表2 计算量对比表

注：选星数为k，可见星总数为N。

不难发现，本文提出的快速选星算法在计算量上明显小于最优选星算法。在高速动态定位、实时姿态测量等领域，提高运算效率是非常重要的。从这个角度讲，快速选星算法具有较大的现实意义，但还需通过GDOP值对选星效果进行评定。

按照本文提出的选星算法选星，在GPS/北斗双模接收机上进行验证，实验结果如图4所示。

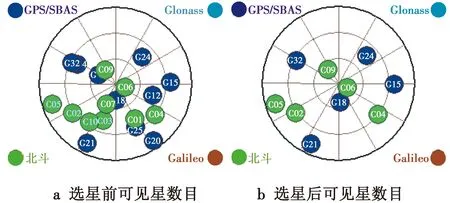
图4 实验结果Fig.4 Experimental result

计算选星后的GDOP值，得到如图5所示的变化曲线。作为对比，图6给出了用最优选星算法得到的GDOP变化曲线。

通过GDOP的仿真图可以看出，快速选星算法得到的选星方案GDOP值基本上能控制在小于2的范围内，个别GDOP值较大时也不超过2.5。要满足卫星导航系统的可用性条件，GDOP值应控制在小于6的范围内，而对于用户定位精度要求较高的情况，需将GDOP控制在小于4的范围内[10]。该快速选星算法能将GDOP控制在小于2.5范围内，其选星效果能够很好地满足导航定位的需求。

图5 快速选星算法GDOP变化曲线Fig.5 GDOP value of fast selection algorithm

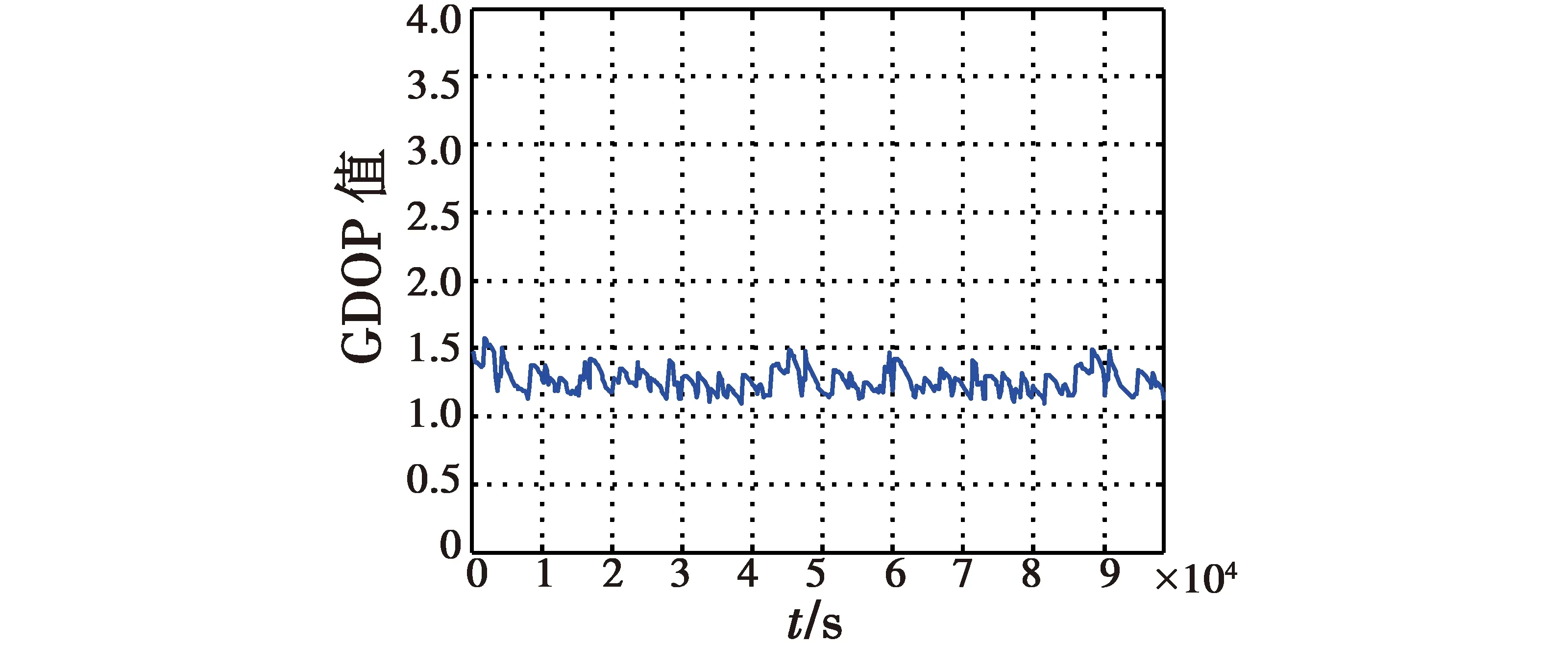
图6 最优选星算法GDOP变化曲线Fig.6 GDOP value of optimum algorithm

通过与最优选星算法相比也可以看出，GDOP的增加量较小，故从选星结果角度看，该快速选星算法也是一种可行的选星策略,可以将其应用于精确测量、快速定位、精密授时等领域。

基于几何分布的快速选星算法，对接收机所在的位置和高度并没有特别的要求，故选星算法本身不受接收机所在位置和高度的影响。但需要指出的是，在接收机周围有遮挡的情况下，卫星的可见性会受到影响，极端情况下，甚至会接收不到足够数量的卫星信号，此时，选星过程已经失去意义。

4 结束语

本文通过对最优选星方案的卫星空间几何分布进行研究，提出了一种综合快速选星算法。充分利用了卫星的高度角和方位角信息及最优选星方案的卫星分布特点，提高了运算效率。仿真结果表明，该快速选星算法选星效果较好，GDOP值始终在可控范围内，以较小的精度损失换来了选星效率的大幅提高,为GNSS接收机在实时性要求较高的动态定位、姿态测量等领域的应用创造了条件。

[1] 周立锋，曹淑艳，姜大治，等．GPS高精度测速算法探讨[J]．电光与控制,2009,16(2)：84-85．

[2] 纪龙蛰，单庆晓．GNSS全球卫星导航系统发展概况及最新进展[J].全球定位系统,2012,37(5)：56-61．

[3] 张强，张晓林，李宏伟，等．组合卫星接收机中的选星算法[J].北京航空航天大学学报,2007，33(12):1425-1426．

[4] 黄继拯，刘红，赵艳，等．GPS/北斗的组合选星算法研究[J]．舰船电子工程,2011,31(8)：82-83．

[5] PRATAP M,PER E.全球定位系统——信号、测量与性能[M].罗鸣，译.2版.北京：电子工业出版社,2008．

[6] ZHANG M Y,ZHANG J.A fast satellite selection algorithm:beyond four satellites[J].IEEE Journal of Selected Topics in Signal Processing,2009,3(5):740-747.

[7] 金玲，黄智刚，李锐，等．多卫导组合系统的快速选星算法研究[J]．电子学报，2009,37(9)：1933-1934．

[8] WEI M M,WANG J,LI J Q.A new satellite selection algorithm for real-time application[C]//International Confe-rence on Systems & Informatics,Yantai,2012:2567-2570.

[9] 许承东,李怀建,张鹏飞.GNSS数学仿真原理及系统实现[M].北京:中国宇航出版社,2011.

[10] 霍航宇,张晓林.组合卫星导航系统的快速选星方法[J].北京航空航天大学学报,2015,41(2):273-276.

AFastSatelliteSelectionAlgorithmforGPS/BDIntegratedNavigationSystem

LIU Shuaia, ZHAO Guo-rongb, GAO Chaob, ZENG Binb

(Naval Aeronautical and Astronautical University,a.Graduate Students’ Brigade;b.Department of Control Engineering,Yantai 264001,China)

To realize fast satellite selection for GPS/BD integrated navigation system,a selection algorithm based on the geometry layout is presented.According to the geometry layout feature of the optimal satellite selection result,the visible satellites are divided into different groups by their azimuth and elevation,and then cost function is used for selecting satellites in each group.Compared with the original optimum satellite selection algorithm,the fast satellite selection algorithm need less computation.The emulation result shows that it works well and can keep the Geometric Dilution of Precision (GDOP) within 2.5.It can satisfy the requirements to precision and real-time performance in the aerospace field.

integrated navigation; satellite selection algorithm; geometry layout; cost function; Beidou navigation system

TN967.1

A

1671-637X(2017)03-0032-04

2016-03-22

2016-04-25

国家自然科学基金(61473306)

刘 帅(1990 —),男，山东烟台人，硕士，研究方向为飞行器综合导航技术。