谐振耦合式无线电能传输系统谐振线圈的优化设计*

2017-12-18仲崇德朱武张乐

电测与仪表 2017年21期

仲崇德，朱武，张乐

（上海电力学院，上海200090）

0 引言

传统的有线电力传输方式存在不少问题，而且不能满足特殊场合的需要，太多的电线和插座给人们的生活带来多种不便［1-2］，这些问题的解决都需要一种脱离电线的电能传输方式。目前，电能无线传输主要有三种方式，分别是电磁感应式，谐振耦合式和利用微波原理方式传输［3-4］。经过多年的发展，感应式的无线电能传输技术比较成熟［5-6］，主要应用于磁悬浮列车［7］，体内医疗器械的供电［8］等，但传输距离比较近，技术应用方面有很多的限制；利用微波原理的无线电能传输距离远，但传输效率很低［9］；与前两者相比，谐振耦合无线电能传输技术的传输距离在两者之间，同时又满足低电磁辐射和电磁兼容的要求［10］，拥有更加广阔的应用前景。因此，国内外很多高校的专家学者们积极开展谐振耦合无线电能传输方面的研究［11-12］。

然而，该技术现在还处于起步阶段，许多理论和实验研究还比较欠缺［13-14］，尤其是关于谐振线圈的参数选取方面。本文从系统耦合模型出发，分析了传输效率和功率与谐振状态、互感以及线圈本身等因素之间的关系，提出了谐振器优化设计方法，并给出了实例仿真，最后设计制作多组谐振线圈，以验证该方法的可行性。

1 系统模型及分析

1.1 系统模型

谐振耦合式电能无线传输系统包括高频电源，发射回路，接收回路和负载，为简化起见，将高频逆变的发射源部分直接等效到发射回路，可得谐振式耦合电路的模型如图1所示。

图1 谐振耦合电路模型Fig.1 Circuitmodel of resonant coupling windings

其中VS为高频电源；R1和R2分别是两回路在高频下的等效电阻；L1和L2是两线圈的电感量；C1和C2是串联谐振电容；RL为负载；M为互感；D为传输距离。

当收发回路中LC的固有谐振频率和发射源的频率相一致时，电路发生串联谐振，此时，电路中的阻抗最低，流过收发线圈的电流最大，在有效的距离范围内，发射回路所发射的大部分能量被接收回路接收；如果收发电路的固有频率与发射源频率不一致时，发射回路大部分的能量不能被接收回路吸收，造成传输效率比较低，即失谐状态。

由图1的耦合电路模型可以得出如下方程：

为了简化起见，将收发回路的阻抗分别记为Z1和 Z2，即：

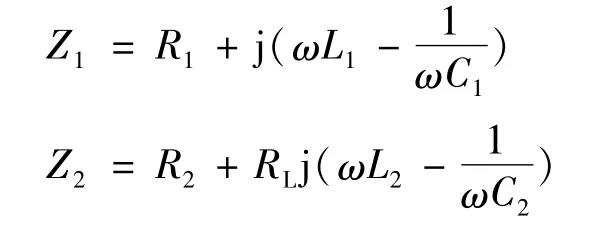
代入式（1），可求得两回路的电流如下：

则发射回路的输入功率Pin为：

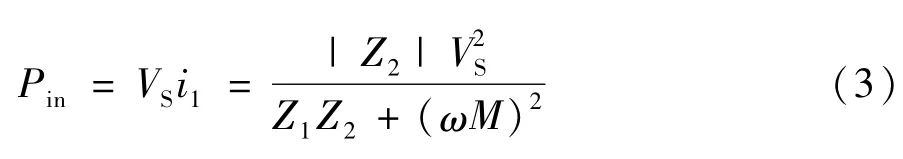
接收回路中RL上的功率即输出功率Pout为：

传输效率为：

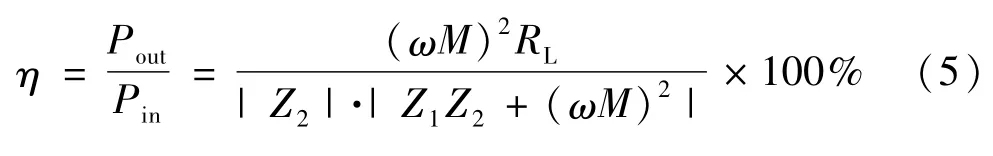
谐振时，有 Z1=R1，Z2=R2+RL，则式（5）又可写为：

通过式（6）和式（7）的比较，可以看出谐振状态时，系统的传输效率最高。

1.2 谐振器传输功率与效率分析

由系统电路模型可以得到传输功率式（4），将Z1、Z2代入得：

从式（8）中可以看出，系统输出功率受多个参数影响，系统频率ω，互感M，高频电源Vs，发射端阻抗R1、X1，接收端阻抗 R2、X2以及负载 RL。由于影响参数比较多，可以分开讨论，假设其它参数均为定值时，考虑单一参数对功率的影响。

1.2.1 谐振状态对传输功率的影响

将其它参数设为已知，考虑谐振对传输功率的影响即是考虑电抗X1和X2对传输功率的影响，讨论式（8）中Pout的极值，由于分子均为已知，只需讨论分母的极值即可。令 N=［R1（R2+RL）-X1X2+（ωM）2］2+［R1X2+（R2+RL）X1］2，显然是关于 X1和X2的二次函数，分别对其求偏导并等于零得：

当（ωM）2-R1（R2+RL）≤0时，方程组（9）有唯一解：X1=X2=0。此时N取得最小值，即在谐振状态时，输出功率最大。

1.2.2 互感对输出功率的影响

系统的其它参数都为已知，谐振器也在谐振状态，即X1=X2=0，谐振频率为ω，可得：

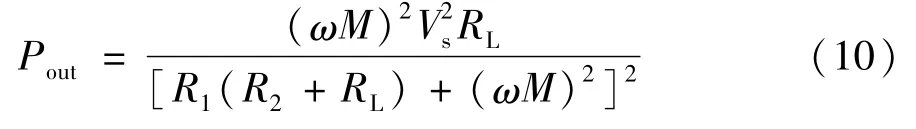
对求导数并令其等于零，得：

图2 互感对输出功率的影响Fig.2 Influence of mutual inductance on the output power

1.2.3 互感对输出效率的影响

在谐振状态下，从式（7）明显可以看出：当M=0时，取得最小值；当M值在一定范围增加时，系统效率η不断提高，M足够大时，输出效率将由负载和接受端等效电阻决定，从而趋于最大值。互感对系统效率的影响如图3所示。

图3 互感对系统效率的影响Fig.3 Influence of mutual inductance on the system efficiency

文中分析了互感值对系统输出功率和输出效率的影响，互感值受两线圈的半径、匝数以及它们之间的距离而决定，所以在系统设计时，两谐振线圈的距离并不一定是越近越好，线圈的匝数和半径也不一定是越大越好，而是应该根据系统的其它参数选择最优值。

2 谐振器参数设计

2.1 谐振器参数

导线在高频状态下的损耗电阻由高频电阻和辐射电阻组成［15］。一方面，电流在导线中的分布并不均匀，存在“趋肤效应”，使导线的有效电阻增加；另一方面，高频交变电流产生电磁辐射，也会有相应的损耗，这部分损耗等效为辐射电阻。高频电阻R和辐射电阻Rr可通过以下公式来计算：

式中ω为系统角频率；μ0为真空磁导率，μ0=4π×10-7H/m；σ为线圈导线的电导率；N为线圈匝数；r为线圈半径；α为导线半径；c为光速，3.0×108m/s；f为系统频率。

本文系统所用频率为1 MHz，辐射电阻远远小于高频电阻，即Rr≪R，所以忽略辐射电阻，线圈电阻近似等于高频电阻R。两平行同轴的密绕线圈参数除了高频电阻外，还包括线圈自感L和线圈互感M，分别由式（14）和式（15）求得［16］：

式中N为线圈匝数；r为线圈半径；a为线圈导线半径；d为两线圈中心之间的距离；

如果确定谐振线圈的半径r0、r1和两线圈的距离即传输距离d，根据式（15）可得：

然后再根据两线圈乘积的公约数选取两谐振线圈的匝数，同时还要兼顾其它元件如电容的电压电流以及MOS管的耐压和耐流值。选定谐振线圈的匝数后，代入式（14）即可计算得出线圈的电感值L。

由于本文线圈采用“密绕”的方式，线圈间的分布电容不足以满足谐振条件［17］，需要外加谐振电容以使线圈谐振频率在1 MHz附近。电容的选择除了满足电容值的要求外，还须满足高频特性，所以本文选择了适用于高频电路的云母电容。由上文确定了线圈的电感L和系统的谐振频率f后，可由以下公式求得谐振电容值。

2.2 参数仿真

本文选择谐振频率为f=1 MHz，直流电源电压Vs=10 V，线圈导线选择直径2 mm铜线，谐振线圈半径r0=0.1 m、r1=0.1 m，传输的距离d=0.2 m，在谐振频率下，忽略辐射电阻，根据上文公式粗略计算高频电阻为0.5Ω，考虑到线路走线和元件的因素，为计算方便，选取等效电阻R=1Ω，选取负载电阻RL=10Ω。在上述参数下，互感对输出功率和效率的影响如图4所示。

图4 互感对系统效率和输出功率的影响Fig.4 Influence of mutual inductance on the system efficiency and output power

根据式（16）得两谐振线圈的匝数乘积N0N1=54.2≈54，取其公约数，并且为了使两回路中的电流不至于过大，两线圈的匝数可分别取6匝和9匝，参数如表1所示。

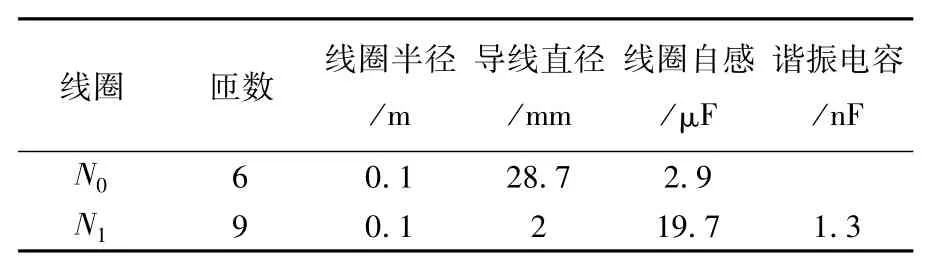
表1 仿真的线圈参数Tab.1 Simulation of the coil parameters

3 实验及分析

为验证上述谐振耦合电能无线传输谐振器参数分析的可行性，本文制作了一个工作频率为1 MHz的谐振耦合系统，线圈参数与表1相同。

实验电路如图5所示，由高频驱动电路产生频率为1 MHz的驱动信号，经单管组成的E类放大器后输出具有一定功率的正弦波，通过发射电路将能量传递到接收电路。其中MOS管采用的是IRF840，和为高频三极管BFG31，Rc为0.1的高频采样电阻，线圈均采用密绕方式。

当发射电路直流输入为10 V/2.6 A时，发射线圈电压和采样电阻上电压如图6所示。

由图6可计算出两电压的相位差大约为，输出电压峰值为161.2 V，采样电阻两端电压峰值为0.36 V。因此计算出发射电路的发射功率为：

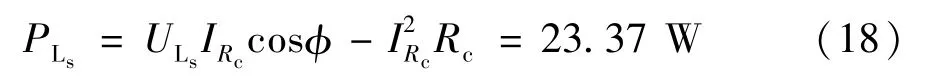
测得此时负载上接收到的功率为14.76 W，那么发射电路到接收电路的效率为η=14.76/23.37×100%=63.2%，由于考虑到线圈有很小的辐射损耗以及设计的误差，故可以认为符合上文理论上计算的接收功率16.27W和效率69.6%。

将发射线圈和接收线圈参数交换，即取发射线圈匝数N0=9，接收线圈匝数N1=6，保持两线圈其它参数和谐振状态均不变。测得直流电源输入为29 W，发射线圈发射功率为23.58 W，负载接收到的功率为14.63 W，系统效率为 η=14.63/23.58×100%=62.0%，可见负载接收到的功率和效率与交换之前的功率和效率基本相同。

图5 谐振耦合无线电能传输电路设计Fig.5 Design of resonant coupling wireless transmission circuit

图6 发射电路输出电压和采样电阻两端电压Fig.6 Output voltage waveforms of Ls and Rc

不断改变两线圈的参数，得到的结果如表2所示。

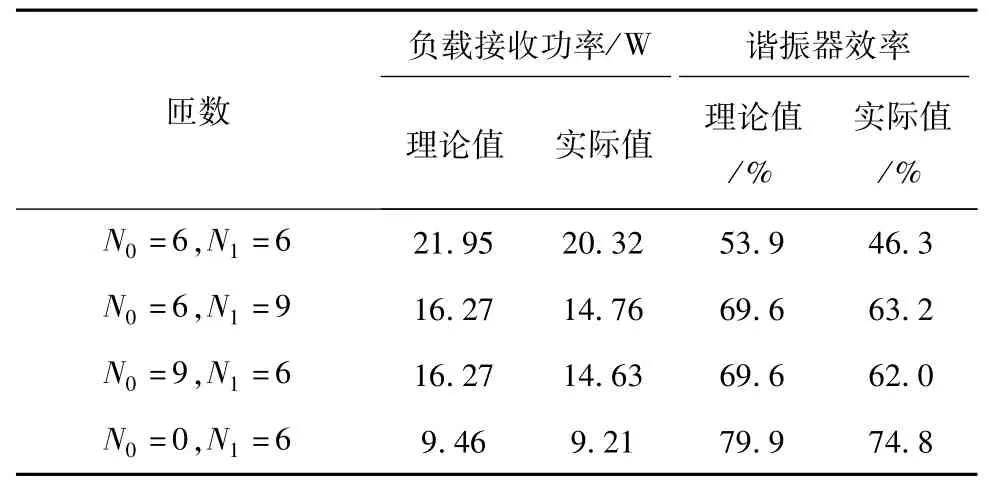
表2 谐振器不同参数下负载接收功率和效率Tab.2 Load receiving power and efficiency under different parameters of resonators

从表2中可以看出，当谐振器两线圈均为6匝时，系统传输功率比较高，但相应的效率却比较低；两谐振器线圈均为9匝时，系统传输功率比较低，相应的效率却比较高；两线圈匝数乘积为定值时，系统传输的功率与效率基本相同。以上表中实验结果和理论值相比较，两者有一定的误差，这主要是理论计算中忽略了线圈小部分的辐射损耗以及硬件设计上的损耗。忽略掉这些误差，实验结果和理论计算值具有较好的一致性。