基于卷积神经网络的绝缘子故障识别算法研究

高强，孟格格

（华北电力大学电气与电子工程学院，河北保定071003）

0 引 言

绝缘子是高压架空输电线路的关键部件之一，由于长期处于运行电压的作用下，加上露天环境腐蚀，绝缘子可能会出现掉串、断裂、污秽等故障，对电力系统影响很大，因此，对故障绝缘子的识别具有重要意义。目前国内外识别绝缘子主要是依据轮廓、颜色和纹理［1-3］等特征来进行，对故障绝缘子的检测方法主要有紫外成像法，红外成像法和电场法。紫外成像法可以有效检测绝缘子放电的故障缺陷，红外成像法可以检测发热故障，电场法仅适合检测存在于绝缘子上较严重的短路性故障，但这样特征提取方式和故障检测方法并不能完全代表绝缘子的情况。卷积神经网络（Convolutional Neural Network，CNN）作为深度学习（Deep Learning）的一种，避免了特征提取的过程，而隐藏地从训练数据中进行学习，这样提取的特征更能全面地代表图像。加上其提出局部感知野、参数共享以及降采样，使其对平移、比例缩放、倾斜等其他形式的变形具有高度不变性。因此，被广泛的应用于如手写体识别［4］、字符识别［5］、人脸识别［6］、交通信号识别［7］、手势识别［8］等领域。

随着CNN的广泛应用，各种问题也被深入研究，很多优化的结构和算法被提出。文献［9］通过重复使用较小卷积核，设计并实现一种新的卷积神经网络结构，有效减少训练参数的数量并提高识别的准确率；文献［10］提出深度卷积神经网络（Deep Convolutional Neural Network，DCNN）结构解决识别中计算量大，特征提取复杂等问题；另外，文献［11］指出，引入ReLU激活函数代替传统的Sigmoid函数和tanh函数，也能够提高网络的识别性能。文献［12］利用主成分分析网络（Principal Component Analysis Network，PCANet）对图像进行预处理，去除图像之间的相关性进而降低对调参的要求，提高识别效果。

目前，关于提升CNN性能和识别率的研究非常多，但很少有从卷积核之间相关性角度研究的。在CNN网络结构中，卷积层的作用是通过不同的卷积核来进行卷积运算提取图像的特征信息，但不同卷积核之间的相关性表明核函数可能提取到相同的特征，会影响提取信息的独立性，而提取相同的信息对识别率的提高并没有帮助。本课题从核函数去相关性的角度出发，改进BP算法，使在不增加核函数数量和网络计算量的基础上，独立且全面地提取绝缘子样本的特征，进而有效的提升绝缘子样本的分类性能。

1 核函数相关性分析

1.1 卷积神经网络的网络结构

卷积神经网络的基本结构如图1所示，它是一个多层的神经网络，每层由多个二维平面组成，每个平面是由多个独立的神经元构成。

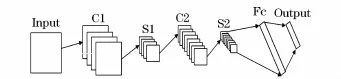
图1 卷积神经网络基本结构Fig.1 Basic structure of convolutional neural network

输入图像经过卷积层C1的卷积运算后，加偏置，加激活进入到降采样层S1，降采样层可以通过多种池化方法得到特征映射图，这些图再进行卷积运算得到C2层，再经降采样得到S2层，S2层经过单层感知机得到Fc并进行全连接得到最终的输出。

1.2 BP算法误差传播分析

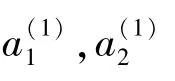
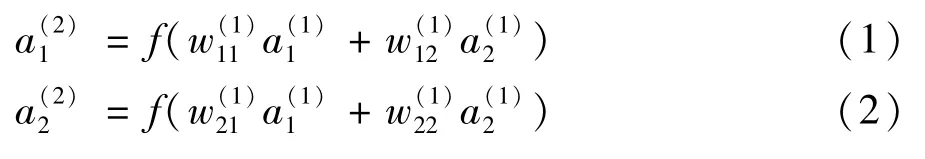
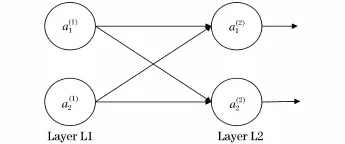
图2 CNN第一层与第二层运算关系Fig.2 Operational relationship between first and second layers of CNN

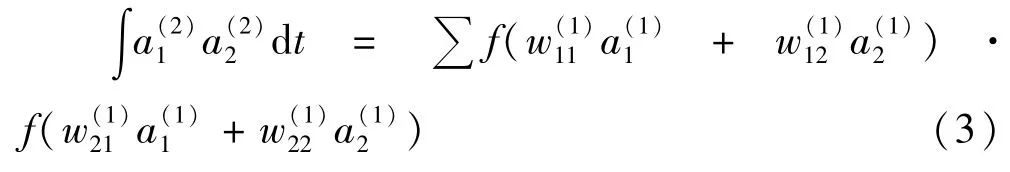
在反向传播中，权值误差的更新公式如下：

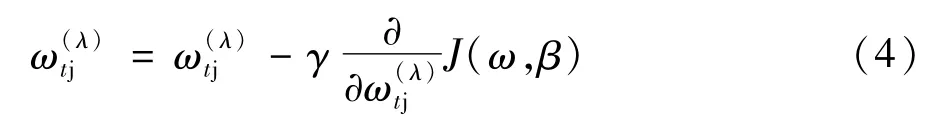
式中γ是学习率；J（w，b）是损失误差函数。误差对权值的导数为：

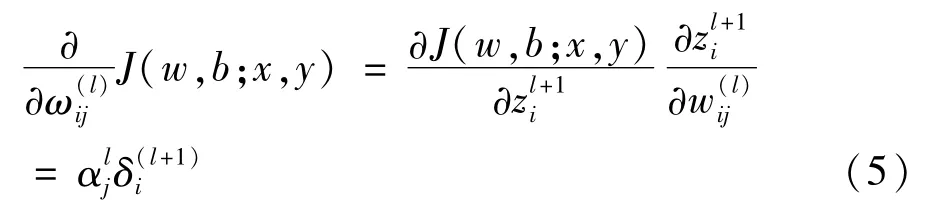
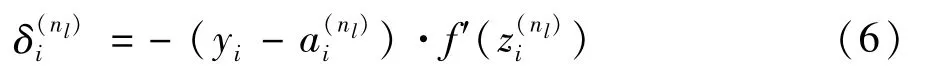
对l=nl-1，nl-2，……，2的各个层，残差的表达式为：

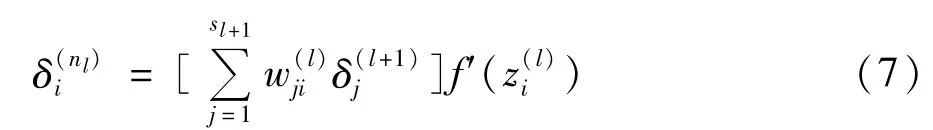
因此，权值误差的修正量可表示为：

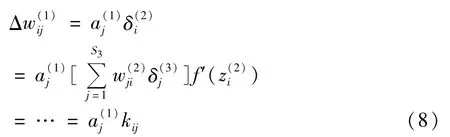
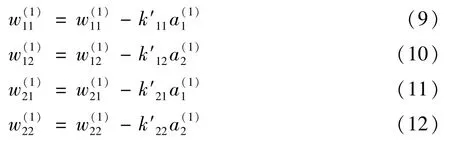
因此，得第二层特征图之间的相关性为：

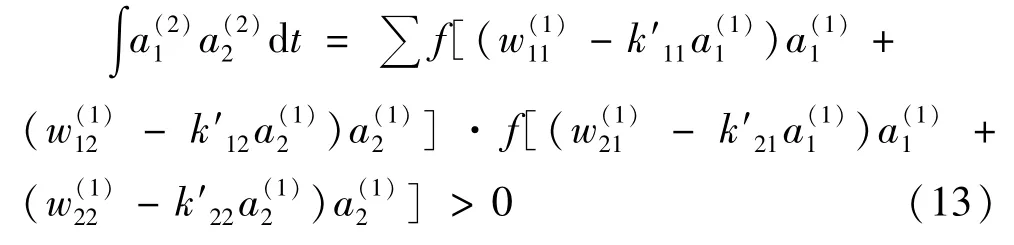
根据信号检测与估值［13］理论，对确知信号进行检测的问题与神经网络的模式分类是一致的。按照一定的准则判定哪个信号的存在，给出了误码率公式为：

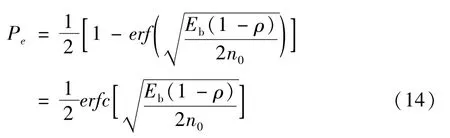
式中ρ是信号间的互相关系数。可见，互相关系数越小，误码率越低。因此，降低第一层输出信号的互相关系数应能提高识别率。根据式（2）可知，第一层输出信号与核函数有关。

1.3 基于向量空间理论的相关性影响的分析

对一幅M×N的图像，可以被看成是M×N维向量空间T中的一个向量a。核函数L×L（L＜min（M，N））维是H空间的向量h，由于L＜min（M，N），因此，H是T的子空间。CNN卷积运算提取特征信息，就是用子空间H表达T的过程，或者，可以认为是用子空间H近似空间T。其近似程度可以用距离来表示。

首先扩展H子空间的维数，使H与T同维，即L+L1=M，L+L2=N，在扩展出来的L1和L2维度上，都填充上0。因此，L空间与T空间的距离可以表达为：

从H空间中任意选择k个核函数向量hi，k个无关向量组可表达的最大维度是k维。假定每一维度用1表示，则k维向量与a的距离为：

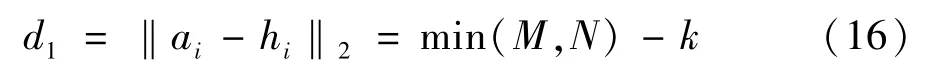
如果k个向量是线性相关的，则k个向量中至少有一个是不独立的，如果k个向量中独立向量个数为k-r（r≥1）个，只能组成一个 k-r维基底，所表达的最大维度是k-r维，与a的距离为：

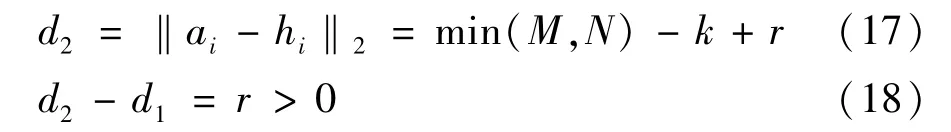
因此，由k个线性相关向量组成的基底，在表达T空间的向量（图像）时，其误差要大于k个线性无关组向量的误差。

CNN卷积运算的过程，其核函数向量的维度（如3×3核、5×5的核）保持不变，而移动核函数的过程相当于其维度范围在改变，即用不同核函数向量组来表达图像，也就是特征提取的过程。按照BP算法进行训练，误差在前向传播时，如果不控制卷积核之间的相关性，核函数向量即可能是线性相关的，也可能是无关的。其结果表现出收敛误差的不同。

寻找具有独立向量的核函数组是减小收敛误差的途径。如何去掉核函数的相关性，需要借助其他数学工具。本文采用小波分解来构造核函数，以保持核函数之间的无关性。

1.4 基于小波分解算法构造

从图像处理角度来看，小波分解不仅可以覆盖整个频域且小波分解通过选取合适的滤波器可以极大的减小或去除所提取的不同特征之间的相关性。本文对核函数进行小波分解，通过去除核函数之间的相关性来保证提取特征之间的独立性进而提高卷积神经网络的识别率。

小波分解后的图像是对原图像“不同分辨率”的表达［14］。即一个图像作小波分解后，可得到一系列不同分辨率的子图像。具体步骤如下：

（1）初始化网络结构以及各连接参数，在第一层卷积核初始化时使用小波分解方法，去除核之间的相关性；

（2）假定选择4个核函数。用训练样本进行BP算法传播，并在误差反向传播到第一层时，用小波分解法对卷积核误差的修改量进行处理。

分成独立块：即将4个核函数的误差修正量加在一起进行小波分解，生成4个完全独立的子块（低频部分分解系数、垂直方向分解系数、水平方向分解系数、对角线方向分解系数），每个核函数分别选取其中一个子块作为修正量；

分成组合块：每个核函数的误差修正量分别进行小波分解，核1的修正量不做处理，核2的修正量去除垂直方向分解系数，核3的修正量去除水平方向分解系数，核4的修正量去除对角线方向分解系数；

（3）把每一次训练的误差给核函数更新时，都按照（2）进行修正。

2 去相关算法的实验验证

实验选用MNIST、CIFAR-10和CK三个标准数据集，并与传统CNN算法比较，验证核函数去相关算法的有效性。

2.1 MNIST库上的实验

MNIST手写体数据库包含70 000张0～9的图片，每类7 000张。其中60 000张训练样本，10 000张测试样本。每个样本均为28×28的灰度图像并直接作为网络的输入。在测试中，采用的网络结构为：4C-（2×2）S-12C-（2×2）S-100F，核函数误差修正方式为组合块。不同尺寸卷积核去相关算法与传统BP算法对应的识别率如表1所示。其中，识别率绝对提升量=本文算法识别率-传统算法识别率，识别率相对提升量=（本文算法识别率-传统算法识别率）/（1-传统算法识别率）。

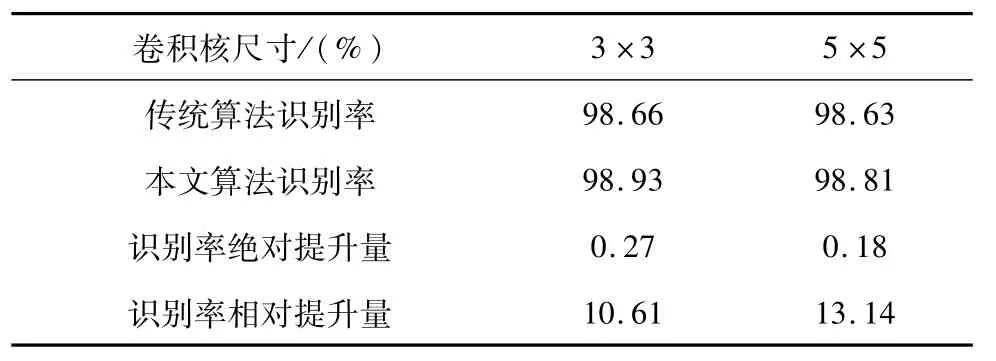
表1 不同尺寸卷积核的网络识别率（MNIST库）Tab.1 Identification rate of different sizes of Kernels（MNIST database）

从表1可以看出，对应不同尺寸的卷积核，本文算法的识别率总是优于传统算法。在3×3和5×5核函数尺寸下，识别率的相对提升量分别为10.61%和13.14%，说明核函数去相关算法通过去除核函数之间的相关性，提取到了样本更加独立的特征，也说明该方法在MNIST库上取得了一定的效果。

2.2 CIFAR-10库上的实验

CIFAR-10数据库包含10类共60 000张32×32的彩色图像，每类6 000张，其中50 000张训练集，10 000张测试集。在网络结构为：4C-（2×2）S-16C-（2×2）S-240F，卷积核尺寸为5×5，核函数误差修正采用组合块的前提下，传统算法与本文算法的网络识别率随着训练次数的变化曲线如图3所示。

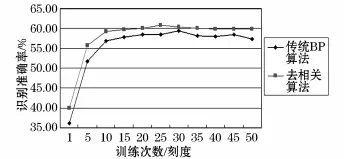
图3 传统BP算法与去相关算法识别率随训练次数变化曲线Fig.3 Curve of recognition rate of traditional BP algorithm and decorrelation algorithm with the change of training times

从图3可以看出，在CIFAR-10数据库上，本文算法收敛速度快于传统算法，且最高识别率60.85%大于传统算法下的最高识别率59.41%，尤其在训练次数比较少时这种优势更加明显，比如在训练次数为5时，传统算法识别率为51.8%，而本文算法可以达到55.69%。

2.3 CK库上的实验

CK库是发布于2010年的cohn-kanada Dataset，共6类1810张图片，实验中选取90%（1629张）作为训练，10%（181张）作为测试。在测试中，采用的网络结构为：4C-（2×2）S-8C-（2×2）S-100F，核函数误差修正方式为独立块。对应不同尺寸卷积核本文算法与传统算法对应的识别率见表2（其中，迭代次数为50）。

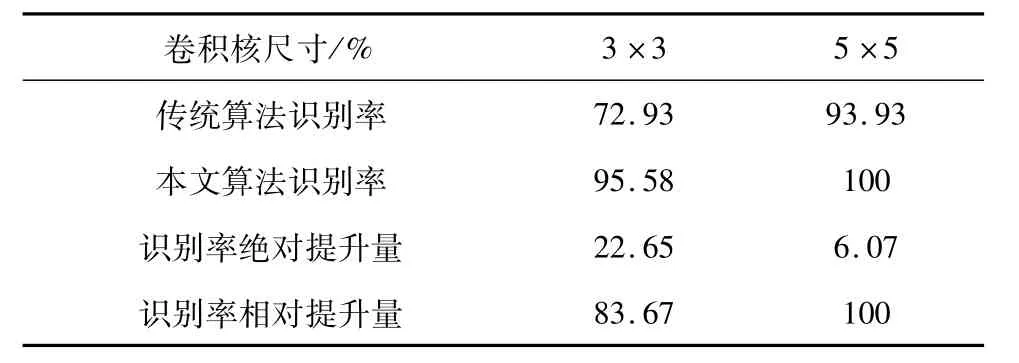
表2 不同尺寸卷积核的网络识别率（CK库）Tab.2 Identification rate of different sizes of Kernels（CK database）

从表2可以看出，本文算法的绝对识别率较传统BP算法分别提升22.65%、6.07%，相对识别率分别提升了83.67%、100%，尤其在5×5的卷积核尺寸下，网络能对样本实现100%的识别。其原因可能是该库中，样本数较少，不同类样本间特征区别明显，而本文算法恰好提取了样本的不同特征，完成对样本100%的识别。

3 绝缘子故障识别的研究

在上述数据集上的实验结果说明，相较于传统算法，该算法能取得更好的效果，除此，能在不同核函数尺寸的条件下取得较高识别率，且此算法达到与传统算法相同识别率的前提下，所需的训练迭代次数更少，训练时间更短。文献［15］将深度信念网络应用在绝缘子故障识别中并取得一定成果，接下来，我们将此算法应用在绝缘子故障识别中。

3.1 绝缘子库的建立

由于目前没有公开的绝缘子数据库，本文采集正常绝缘子和故障绝缘子来建立数据库。该库中有1 200张绝缘子图像，包括800张正常绝缘子，400张故障绝缘子（包括掉串、放电痕迹、断裂、污秽等）。为保证CNN网络的泛化性，库中绝缘子的大小、形状，受光照强度等各不相同，且对样本做了旋转、缩放等处理。库中部分正常绝缘子样本和故障绝缘子样本如图4、图5所示。

图4 正常绝缘子图像Fig.4 Images of normal insulators

图5 故障绝缘子图像Fig.5 Images of faulty insulators

3.2 绝缘子故障的实验

3.2.1 绝缘子故障识别过程

实验中从800张正常绝缘子中随机选取600张作为训练样本，剩下200张作为测试样本，同样，从400张故障绝缘子中随机选取300张作为训练样本，剩下100张作为测试样本。将样本大小均归一化为64×64，作为CNN的输入。

确定好训练集和测试集后，对网络进行初始化，网络结构初始化为：4C-（2×2）S-8C-（2×2）S-100F，两个卷积层核函数尺寸均为5×5，batchsize的大小设为30。

在第一个卷积层初始化时，对四个核函数分别进行小波分解处理，每个核分别选取小波分解后的不同子块。

用训练样本进行BP算法传播，并在误差反向传播到第一层时，用小波分解法对卷积核误差的修改量进行处理，在这里，核函数的误差修正方式采用组合块，网络训练完成后，对测试集进行测试，并计算网络识别的正确率。

3.2.2 实验结果

在3.2.1的结构和参数前提下，当训练的迭代次数从10次变化到50次时，本文算法和传统算法对训练样本和测试样本的识别率如表3所示。

由表3可以看出，随着训练的迭代次数增加，两种算法对训练样本和测试样本的识别率均呈上升趋势，对传统算法来说，当迭代次数增加到40次时识别率基本保持不变，对本文算法来说，当迭代次数增加到20次时，识别率即可保持基本不变。且就识别率而言，该算法能对训练样本实现100%识别，由于传统算法对测试样本的最高识别率99.77%，该算法对测试样本识别率也以98.33%高于在传统算法下的96.67%。在本实验中，传统算法达到收敛（迭代次数为40）所需要的时间为4.13 m，本文算法达到收敛（迭代次数为20）所需要的时间为2.12 m。综上，该算法在对绝缘子故障的识别中，从识别率和收敛速度而言，均优于传统算法。

表3 迭代次数对识别性能的影响Tab.3 Effect of iteration number on recognition performance

3.2.3 实验结果理论分析

用互相关系数来表示特征图之间的相关性，互相关系数值的范围在-1～1之间，为负代表两个图像呈负相关，为零代表不相关，为正代表正相关。传统算法和本文算法下，对应特征图之间互相关系数值如表4所示，在此，选取5个样本特征图之间的互相关值来做对比。

表4 不同样本特征图之间互相关系数Tab.4 Cross correlation coefficient of different samples

由表4可以看出，对应不同样本，此算法下特征图之间的相关性均小于在传统算法下，结合1.2和1.3的分析，说明核函数去相关算法能更有效提取相互独立的特征图，获取更多的信息，这对于提高网络的识别性能也更有力。

3.2.4 与其他算法的比较

为验证该算法在绝缘子故障识别中的有效性，实验将该算法与文献［16］的3-CNN，文献［17］的CConvNet以及文献［18］提出的算法进行对比。本实验中，3-CNN算法采用的网络结构为：4C-（2×2）S-6C-（2×2）S-6C-（2×2）S-100F，CConvNet算法采用的网络结构为：2C-4C-（2×2）S-6C-8C-（2×2）S-100F，将该算法与文献［18］提出的算法结合，在网络训练时，也对核函数进行去相关性处理。不同算法的识别性能如表5所示。

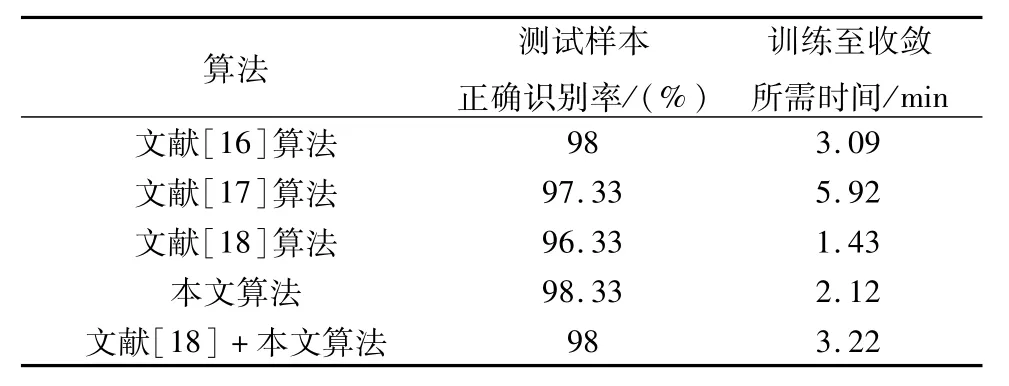
表5 不同算法识别性能比较表Tab.5 Comparison table of the classification performance among different algorithms

从表5可以看出，该算法在识别率上明显优于其他算法，且将该算法与其他算法相结合，识别效果也得到进一步改善，如将文献［18］算法与该算法相结合后，文献［18］的识别率由96.33%提升至98%。从训练至收敛的时间来看，文献［18］所需时间最短，但其识别率仅有96.33%，说明网络结构简单、提取的特征不够全面，虽然节省了训练的时间却造成了更多的错误识别。综上，该算法在绝缘子故障识别中表现出不错的效果，具有一定的应用价值。

4 结束语

文章基于改变卷积核对图像特征的表达，提出了通过小波分解去除核函数相关性的算法。用较少且不相关的卷积核来独立、全面地提取图像的特征，实现更好的识别效果。MNIST、CIFAR-10和CK数据集上的实验表明，此算法不仅可以提高识别率而且能加快收敛速度。最后将此算法应用在绝缘子故障识别中，说明此算法具有一定的有效性和可行性。