基于卡尔曼滤波预测的电动汽车分时租赁监测数据去人为干预技术研究*

龙弃，侯兴哲，肖剑锋，孙洪亮，刘永相，朱彬

（国网重庆市电力公司电力科学研究院，重庆401123）

0 引 言

电动汽车凭借其清洁环保的优势，迅速受到国内外的广大关注［1］。而分时租赁业务凭借其减少车保有量、增加车共享量的绿色环保作用，逐渐受消费者所接受。因此，各地电动汽车分时租赁行业正蓬勃发展，其多级管理平台纷纷建立。总管理平台具有集中采集车速、里程、SOC电量百分比、地理位置、时间、温度等车辆状态信息的管控作用，同时为大数据分析研究奠定了坚实的数据基础［2］。

预处理技术作为数据分析的基础，对所采集的参数起着至关重要的作用。例如，车速反映了驾驶员违章违规情况，时间、里程、SOC电量百分比反映了经济收益情况，温度反映车辆安全问题等，这些数据都存在人为干预的可能性。大型电动汽车分时租赁管理平台一般采用多级管理结构，平台间采用无线通信方式，数据所有者出于隐私保护、规避责任等目的考虑，监测数据在传输过程中进行人为的数据干扰［3-4］，给安全、法律、经济带来极大隐患。因此，有必要根据对所采集的数据进行再预测，以检验其真实性，还原得到最优预测结果。

其中，车速作为车辆管理的核心参数，车速预测受到国内外学者的极大关注。常规的车速预测方法主要包括以下三种：（1）根据采集的公路平曲线半径和纵坡度等线形数据和样本车速，利用回归模型［5-7］、学习型算法［8-9］等预测公路可能出现的运行车速。刘硕，王俊骅等［10］通过多元逐步线性回归建立城市地下道路运行车速预测模型，研究地下道路中车速的分布特征及运行车速。魏朗、陈涛等将驾驶人的道路线形感知和车速进行模糊量化并通过多组模糊规则对车速进行预测［11］。（2）仅根据四个车轮传感器的轮速信号，利用最大轮速法［12］、斜率法［13］、综合法［14］、递推法［15］、非线性滤波法［16］等确定参考车速。（3）基于轮速和其他传感器，即轮速与纵向加速度、横向加速度、横摆角速度等信号，利用卡尔曼滤波等算法为基础的数学模型确定车辆参考速度［17-19］。徐进等建立了考虑侧向容许加速度、纵向加速度、制动减速度、制动热衰退和环境速度与线形参数关系的模型，计算了期望速度［20］。赵治国等结合电子稳定程序系统传感器信号，基于车辆动力学模型和轮胎模型，设计融合驱动轮转矩信息和传感器信息的车速估计算法［21］。

传统车速预测所需的参数均为原始数据，可保证其真实性。但在平台与平台间的无线通信过程中存在一定人为干预的可能，相应的预测结果也会随之变化，不具有任何抗干扰能力。因此，根据受干预影响的采集数据而得到最优预测车速的算法研究较少。为了保证大数据分析数据源的有效性，有必要采用一定的算法进行数据预处理。

文章结合电动汽车分时租赁管理平台的数据采集方式，采用人为干预概率曲线量化监测数据与协方差比间关系，将人为干预概率曲线区间和观测量关系作为输入，建立了回归对象决策树并引入传统卡尔曼滤波算法，从而提出基于决策树分析的卡尔曼滤波预测方法，并应用于车速预测领域，为电动汽车分时租赁管理平台数据预处理奠定了理论依据和有效地实现大数据分析奠定坚实的技术支撑。

1 电动汽车分时租赁管理平台

重庆市电动汽车分时租赁服务平台定位于重庆市大型综合公众服务平台，主要服务于社会用户、服务运营商和政府机构，用于整合集成社会服务资源，提供全套业务服务，给政府提供新能源基建相关数据、商业运营环境数据、用户商业信用评价数据等信息，为要害部门的政策制定与决策提供技术支撑。平台结构框架如图1所示。

本平台内部架构主要分为基础数据采集管理平台和运营服务支撑平台两个部分。数据采集管理平台负责采集管理基础服务设施的信息数据，主要依凭于直接接入平台的监控终端和第三方平台的输入，主要包括车辆资源信息数据、充换电资源数据、车位资源数据和其他资源数据。运营服务支撑平台构建于基础数据采集管理平台的上层，用于为社会用户和服务运营商提供安全稳定的商业交互渠道，主要包括汽车租赁服务、充换电服务、车辆停泊服务和其他第三方增值服务。

本平台提供直接接入本平台的业务服务和提供第三方服务接口实现平台与平台对接的第三方服务等两种接入方式。其中，平台与平台对接方式的数据传导过程中，为了隐瞒超速违规事故、规避违规事故、肆意增加经济收益、隐瞒车辆安全问题等以达到增加商业利益的目的，有一定概率会通过程序或人工方式对真实采集数据进行人为干预。特别的，车速作为车辆管理的基本参数，其涉及法律层面问题，有必要研究一种算法根据总平台所获得的数据（可能受到人为干预）预测其人为干预前的真实值，从而消除人为干预影响。

图1 重庆市电动车分时租赁管理平台Fig.1 Configuration of Chongqing electric vehicle time-sharing lease management platform

2 传统卡尔曼滤波算法

传统卡尔曼滤波算法是一种以最小均方误差为最佳估计准则，采用信号与噪声的状态空间模型，利用前一时刻的估计值和当前时刻的量测值来更新对状态变量的估计，求出当前时刻的估计值，算法根据建立的系统方程和量测方程对需要处理的信号做出满足最小均方误差的估计［22］。

因此，卡尔曼滤波算法是一种循环更新算法，具有数值解的预估-校正能力，其可分为两个部分：时间更新方程和测量更新方程。时间更新方程可视为预估方程，测量更新方程可视为校正方程。其离散卡尔曼滤波器时间更新方程如下所示：

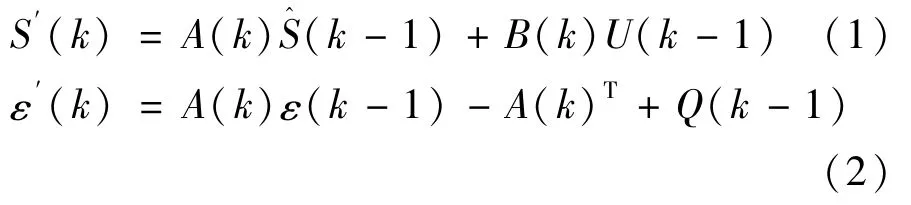
式中 S′（k）是先验估计值；是后验估计值；U（k）是系统控制输入；A（k）、B（k）均为状态变换矩阵；ε（k-1）为上一时刻最优估计值；随机信号w（k）和v（k）分别表示过程激励噪声和量测噪声。假设随机信号均为相互独立、正态分布的白色噪声：

实际系统中，过程激励噪声协方差Q和量测噪声协方差R可能会随每次迭代计算而变化，但变化方式则需根据实际情况而定。

离散卡尔曼滤波器状态测量更新方程：

式中 H（k）是卡尔曼增益；C（k）是状态变换矩阵；X（k）是量测值。

一次时间更新程序和测量更新方程计算后，整个过程再次重复，上一时刻所计算得到的后验估计被作为下一次计算的先验估计，循环往复，逐渐逼近回归对象，从而最终得到最优估计值。

然而，电动汽车分时租赁管理平台的采集数据中，根据量测值与限值（例如量测车速与违章限值）之间的关系，使得量测值可能受到人为干预的影响，从而导致量测值不再是最优回归对象。因此，传统的卡尔曼滤波算法因其回归对象固定而不再适合该问题，需要进一步改进算法该公式，使其回归对象具有自动选择性。

3 采集数据人为干预概率曲线

实际上，不是所有采集数据都具有人为干预的可能。本文以车速为例进行说明。当速度远低于违章车速限值时，几乎不会出现数据人为干预的情况，此时的量测值极大概率是真实值。但是，随着车速的增加，车速数据被人为干预的概率逐渐增大。特别地，为了让人为干预后的结果合理化、平滑化，在违章车速限值附近时，人为干预的概率陡然增加。而当所测采集车速数据逐渐增加，超过违章车速限值后，发生数据人为干预的概率反而逐渐减小，此时更倾向于相信该量测值的真实性。

因此，采集数据人为干预心理动机基本满足高斯函数变化规律，因此不妨设置人为干预概率曲线满足以下高斯公式：

式中a/b决定了正态分布曲线的宽窄，经过多次试验可知，本文采用a=3.5；b是违章车速限值，km/h；c是被研究车辆的最大车速值，km/h；k是数据人为干预概率曲线最大幅值，不妨k设为1。

根据图2的高斯曲线特性可知，当量测车速值为该路段违章车速限值的0.663 6和1.336 4倍时，量测车速值中有50%概率受到了人为干预的影响；当量测车速值为违章车速限值附近时，人为干预概率陡增。但随之，若量测数据大于违章车速限值时，反而人为干预概率逐渐减小，直至0附近，此时量测车速可信度反而增加，说明其未对上传的监测数据实施人为干预行为。该曲线规律与实际情况所述的变化规律一致，因此该概率曲线是合理的。

图2 车速数据人为干预概率曲线Fig.2 Human intervention probability curve for speed data

从图2可知，根据50%概率的两条x轴垂直界限可将车速数据人为干预概率曲线分为区间①和区间②等两部分，即区间①的人为干预概率较低，其结果倾向于量测值，而区间②的人为干预概率较高，很有可能发生数据人为干预。

4 基于决策树分析的卡尔曼滤波预测方法

为了将卡尔曼滤波算法应用车速预测领域，时间更新方程、状态更新方程中变量均需进行调整。

4.1 时间与状态更新方程

时间更新方程：

式中 V′（k）是速度先验估计值（k）是速度后验估计值；am（k）是量测加速度作为系统控制输入；式（1）～式（6）中 A（k）在本文中为单位矩阵；B（k）是状态变换矩阵，本文为采样时间△t；ε′（k）是预测值的协方差；ε（k-1）为上一时刻速度最优估计值。

时间与状态更新方程中，随机信号w（k）和v（k）仍分别表示过程激励噪声和量测噪声。过程值是基于量测加速度和经验计算公式得到（本文称为理论车速值）。假设随机信号均为相互独立、正态分布的白色噪声，仍满足式（3）～式（4）关系但实际系统中，过程激励噪声协方差Q和量测噪声协方差R是不定的，需要进一步量化。

离散卡尔曼滤波器状态测量更新方程：

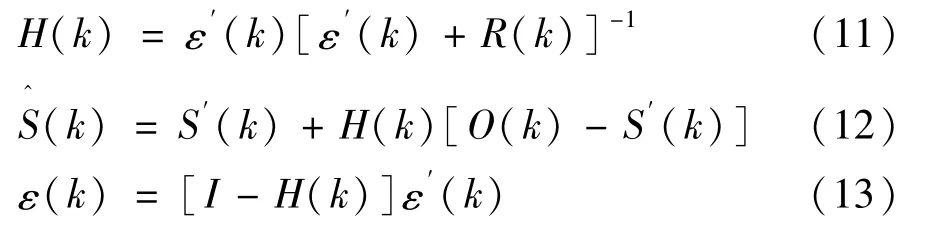
式中 H（k）是卡尔曼增益；式（5）～式（7）中C（k）在本文中为单位矩阵；O（k）为回归对象，而非式（6）中固定的量测值X（k）。这是因为量测值可能受到人为干预的影响，因此与传统卡尔曼滤波算法有所不同。且回归对象根据违章车速限值与量测值之间关系而有所变化。

综上，噪声协方差R、Q与回归对象O（k）均与量测值、理论值、限值间有紧密的关系，本算法中将充分考虑以上影响因素，从而通过多次迭代得到最优预测值

4.2 噪声协方差及协方差比S

根据式（2）和式（5）可知，过程激励噪声协方差Q和量测噪声协方差R的大小直接影响协方差估计值ε′（k）和卡尔曼增益 H（k）。因此，不妨设过程协方差Q与量测协方差R之间的比值为S，即当S越小，则最终结果更偏向于量测值，反之偏向于过程值，即理论值：

4.3 回归对象决策树

回归对象不仅受反映人为干预概率曲线的协方差比值S影响，同时还与理论车速v理、量测车速v测及违章车速限值w等观测量间的关系有关，不同条件下的回归对象决策树如图3所示。

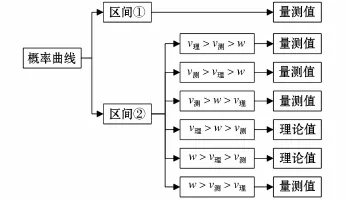
图3 回归对象决策树Fig.3 Decision tree of return object

由反映人为干预概率曲线的协方差S和多种车速关系所构成的回归对象决策树融入传统卡尔曼滤波算法中，从而得到基于决策树分析法的卡尔曼滤波算法。利用该算法所得到最优预测结果可有效减少人为干预因素的影响，获得可信度更高的车速源数据，以达到对运营总平台所采集的数据预处理的目的，为有效地实现大数据分析奠定坚实的技术支撑。

5 算法验证

采用文献［23］的量测加速度曲线，其试验车辆沿直线行驶，经历了“加速-制动-滑行”操作。通过经验公式（17）计算得到理论值，理论、量测、文献数据曲线对比如图3所示。

为了研究该算法的有效性，将参考文献［22］中的加速度等比例放大以扩大速度范围，为验证多种违章速度限值下的预测车速效果提供基础。

从图4可知，0.5 s采集周期加速度与量测加速度基本一致，而1 s采集周期加速度相比量测加速度更为平滑，有一定差距。但是，实际运营中，为了降低通信流量成本，采集周期难以满足0.5 s的要求，基本均在1 s及其以上。为了结合实际情况，本文采用1 s采集周期得到的量测加速度进行研究。

图4 加速度曲线［22］Fig.4 Acceleration curve based on literature［22］

分别将违章车速限值设置为50 km/h、80 km/h，其理论速度、预测速度、量测速度分别如图5所示。

图5 违章车速限值为50 km/h的对比分析图Fig.5 Curve comparison analysis under speed limit of 50 km/h

当违章车速限值设置为50 km/h时，理论值、量测值、预测值速度曲线变化情况如图5（a）所示。其中，理论值是按1 s采样周期采样（如图4所示）的加速度计算得到。为了模拟理论值与量测值相差的特殊情况，量测值是在理论值基础上进行了波动调整以扩大其数值差别和考虑更多可能的情况。

由图5（a）可知，0 s～3 s段量测车速较低，其值约为10 km/h～30 km/h，距违章车速限值50 km/h较远。根据图2可知，属于区间①范畴，协方差比S取2，该速度下人为干预概率低，此时量测值可信度高，故决策树结果是以量测值为回归对象。车辆加速过程中，量测车速逐渐增加，人为干预概率随之增加，此时属于区间②范畴，协方差比S取0.5。进一步，区间②中理论速度、量测速度与车速限值关系复杂，4～6 s时段中理论值高于量测值，由于人为干预概率风险较高，选择理论值为回归对象，递归过程如图5（a）的4 s～6 s时段所示。而在7 s～15 s时段中，量测值高于理论值，其决策树结果为量测值，此时预测值最终向量测值回归。车速进而增加，当量测值高于车速限值50 km/h后，根据图2可知人为干预概率开始下降，量测值可信度回升，预测值的回归对象依旧为量测值，如16 s～26 s区间所示。当车速下降后，虽然速度降到车速限值50 km/h附近，人为干预概率极大，预测值向理论值回归，而在远低于违章车速后重新向量测值回归，通过图5（b）中速度偏差绝对值可直观说明以上变化规律的正确性。

当违章车速限值设置为80 km/h时，理论值、量测值、预测值速度曲线变化情况如图6（a）所示。

图6 违章车速限值为80 km/h的对比分析图Fig.6 Curve comparison analysis under speed limit of 80 km/h

理论值、量测值均与图5（a）中一致。由图6（a）可知，0 s～7 s和27 s～35 s两时间段内，量测车速较低，其值约为10 km/h～45 km/h，距违章车速限值80 km/h较远，属于区间①，故回归对象为量测值。加速过程中车速持续增加，在8 s～17 s时间段内，属于区间②范畴而S取0.5，且量测值高于理论值，决策结果仍为量测值。进而，在18 s～22 s区间时，S取0.5，理论值高于量测值，且在限值车速附件，此时人为干预的概率较大，有故意调低了数值嫌疑，因此预测值向理论值回归逼近。而在23 s～26 s时间段内，仍属于区间②，虽然人为干预概率仍然较高，但量测值高于理论值，最终决策结果是以量测值为回归对象，预测值逐渐向量测值回归逼近。通过图6（b）中速度偏差绝对值可直观说明以上变化规律的正确性。

综上，通过两种不同违章车速限值条件图5（b）和图6（b）的对比可知，本算法能够很好起到智能地选择回归方向的作用，还原得到可信度较高的最优预测曲线，有力地打击数据人为干预行为，为大数据分析提供有力的保证、奠定了坚实的技术基础。

6 结束语

提出根据人为干预概率曲线以量化速度与协方差比间的关系，建立了人为干预概率曲线区间和观测量关系作为输入的回归对象决策树，改进了传统算法，提出了基于决策树分析的卡尔曼滤波预测方法，从而完善基于卡尔曼滤波预测的电动汽车分时租赁监测数据去人为干预技术研究，并结合文献数据和模拟数据，验证了其有效性，并得到以下结论：

（1）低速时，人为干预概率较低，可信度较高，回归对象以量测值为主。但在违章车速限值附近时，回归对象则需根据量测值、理论值、限值间的关系进行选择，不再是单一以量测值或理论值为主；

（2）该方法适应于设置不同的违章限值。根据不同违章车速限值，该算法可自动根据人为干预概率曲线与回归对象决策树的判断结果进行计算，从而智能向可信度更高理论值或量测值进行回归逼近，最终构成最优预测车速曲线；

（3）该方法可扩展至温度、里程等其他车辆状态信息，只需根据参数的特点调整时间更新方程和决策树中的参数关系即可。