针对电网电压扰动的Vienna整流器复合控制方法*

王春阳，姚钢，殷志柱，周荔丹

（1.上海交通大学电气工程系，上海200240；2.上海电气集团股份有限公司中央研究院，上海200070）

0 引 言

三相PWM整流器以其高功率因数的特点，成为许多学者研究的热点［1］。相比于传统PWM整流器，Vienna整流器效率高，具有良好的可靠性，在能量单向流动的高功率密度场合得到广泛应用［2-3］。由于新能源技术和直流微网的快速发展，交直流混合电网在未来电力系统中占据的比重也会越来越大，Vienna整流器可以通过交流主网对直流电网进行供电［4］。若交流电网中存在谐波，则会部分注入直流微网中［5］，其中的谐波电流会引起直流侧电压的波动，进而影响直流电网的供电可靠性，同时直流电网也会反作用于交流电网，产生更大的危害。因此整流器对于电能质量问题的应对显得尤为重要。

文献［6］采用虚拟磁链进行定向，其中的积分器容易受到谐波干扰产生定向偏差。文献［7］针对电网电压严重不平衡情况，通过注入功率纹波改变电流参考值，但控制较为复杂。文献［8］针对三相四线制Vienna整流器，提出了基于物理解耦模式下的控制方法，文献［9］引入了混合导通模式下的电压前馈控制方法，二者控制算法简单易行，但同样仅仅基于理想电压条件，对于谐波等电能质量问题应对不足［10］。

文中基于三相四线制Vienna整流器，采用解耦模式的控制方法，简单灵活，通用性强。由于传统控制方法在处理电能质量问题和提高电流跟踪精度两方面应对不足，因此本文对之加以改进。针对电网背景谐波以及电力电子器件运行引起的电压凹陷问题，引入一种改进型电流跟踪方法，控制简单，同时可有效应对电能质量问题。针对传统的PI控制跟踪精度有限的问题，提出了一种基于PI控制和重复控制的复合控制方法，对电流环加以改进。与传统方法相比，该方法既能保持较好的动态性能，也能够有效抑制电网谐波电压对网侧电流的影响，有效解决电能质量问题［11］。网侧电流谐波含量的降低也能减小直流侧电压波动，维持良好的输出特性。最终的仿真和实验结果验证了所提方案的正确性。

1 三相四线制Vienna整流器工作原理

三相四线制Vienna整流器主电路拓扑如图1所示。

图1 三相四线制Vienna整流器拓扑结构Fig.1 Topological structure of three-phase-four-wire Vienna rectifier

图1中，三相电压源中性点与直流侧电容分裂点相连，构成三相四线制系统。Sa，Sb，Sc为双向功率开关，由IGBT与一个二极管整流桥组成［12］。对于三相对称系统来说，输出电压纹波小且稳定性强，相间扰动对于输出电压影响较小，因此可以实现三相物理解耦，电路等效为三路输出并联的单相三电平PFC电路，从而可以进行单相控制，控制方法简单灵活，适用性强。传统单相控制结构如图2所示。

图2 三相四线制Vienna整流器传统控制结构（单相）Fig.2 Conventional control structure of three-phase four-wire Vienna rectifier（single phase）

2 电压谐波与塌陷情况下的电流跟踪方法

由于用电负荷多种多样，电网在运行过程中会受到干扰，产生电能质量问题。其中电压谐波问题和电力电子器件运行产生的电压塌陷问题比较普遍。

当电网中接入由晶闸管桥构成的整流性负载时，电网电压会在晶闸管开断瞬间出现周期性凹陷，由此可以模拟出电压塌陷波形。对塌陷波形进行FFT分析，可以得到其除了基波分量外，还含有较多的高次谐波分量，其中以5，11，17次谐波为主。因此电压塌陷问题也可以看作是理想基频电压中，混入了高次谐波。

当电网电压中存在背景谐波，按照传统电流跟踪方法，此时的电压采样信号含有谐波信息，由此作为电流参考信号，跟踪出的电网电流也一定含有谐波分量。因此对电流跟踪方法做出改进，采用锁相环提取电压信号基频分量的相位信号，作为电流信号的参考信号。理想情况下，电网电流可以有效跟踪该信号，实现正弦无畸变。

以电压正半周为例，运用状态平均法［13］可以得到电路的平均状态方程：

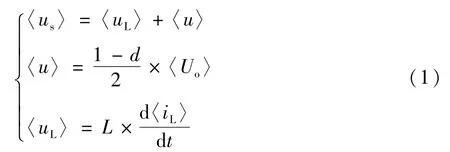
式中d为双向开关占空比；〈x〉为该电气量开关周期内的平均值。当电压us为理想电网电压时，此时电网电流能够完美跟踪基波电压信号，因此电感电压uL与开关处电压u均为理想正弦信号。而当电网电压存在谐波或因电力电子器件运行而产生波形塌陷时，us降低，u不变，因此uL降低，从而导致iL降低。此时电流环发挥作用，iL低于iref，控制信号占空比升高，u降低，最终保证uL稳定，iL维持原来正弦波形。由此保证谐波电压下电网电流仍为基波正弦值，且以单位功率因数运行。电流环具体调节过程如图3所示。

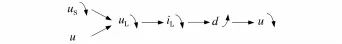
图3 谐波电压调节过程Fig.3 Harmonic voltage regulating process

3 复合控制理论分析

传统控制方法电流环采用PI控制器进行跟踪，具有快速性，但跟踪误差较大。尤其当电网电压存在背景谐波时，PI控制不能保证电流完美跟踪参考信号，导致网侧会存在一定的谐波电流。因此引入基于内模原理的重复控制器，可以有效抑制周期性扰动［14］，改善跟踪效果。虽然重复控制对于周期性扰动信号抑制效果较好，具有较好的稳态精度，但其修正过程以工频周期为步长，动态过程较长。因此本文采用PI控制与重复控制器并联的控制结构，既保留了PI控制的快速响应通道，同时也提高了跟踪精度，可以有效抑制谐波电压干扰。

图4 复合控制电流环结构Fig.4 Hybrid control system current loop structure

图4中，iref为电流参考信号；iL为实际电感电流；ierr为偏差电流；z-N为周期延时环节；Q（z）为辅助补偿器；S（z）为受控对象补偿器；zk为超前环节；PI为比例积分控制环节；K为占空比到电压比例系数，其值为Uo/2。

由图4可知，复合控制方法采用PI控制与重复控制并联的模式，共同对电流跟踪误差信号进行作用。稳态情况下，误差信号较小，跟踪效果良好。当出现负载突变或者较大扰动时，实际电流偏离参考值，此时PI迅速做出反应，改善跟踪效果。一个周期后，重复控制检测到跟踪误差ierr，内模对于误差进行逐周期累加，直到最终ierr趋向于0。通过PI控制的快速响应与重复控制的精准跟踪，可以实现更好的控制效果，改善电流波形质量。

计算图4中闭环脉冲传递函数为：

其中：

对于离散控制系统，当且仅当特征方程的所有根都位于单位圆内，系统才能稳定。但本文中基频fs=50 Hz，采样频率 fc=20 kHz，N=400，属于高阶方程，因此采用另一种方法判断稳定性。可以将方程（4）转变为：

设（i=1，2...，N）为特征方程的根，若|zi|＜1，则|zi|N＜1。我们定义 H（z）=|Q-C（z）P（z）|，这样可知当H（z）＜1时，系统必然稳定。

式（5）中 Q按照工程经验取 0.95［15］，P（z）可以看成系统的等效控制对象，因此需要设计合理的补偿函数S（z）对被控对象进行补偿，以实现控制目标。由P（z）幅频特性可知，在中低频处存在-40 dB的增益，相位不存在滞后，所设计的二阶滤波器S（z）应满足补偿后低频相互抵消，高频衰减的原则。可以看出S（z）P（z）在低频段增益为零，高频段快速衰减，但是 S（z）P（z）在中频段存在一定相位滞后，因此引入超前环节zk对相位进行补偿，该环节对幅频特性曲线无影响，k的大小取决于 S（z）和 P（z）总的相位偏移。由图5中可以看出补偿后的zkS（z）P（z）在幅频曲线上，在低频处零增益，在中高频处迅速衰减。在相频曲线方面，在中低频处无相位偏移。最终保证系统对于工频信号无衰减，对于工频的谐波信号具有明显的抑制效果。基于以上分析，在采样频率为20 kHz时，针对P（z），本文设计的补偿函数为：

由图5可知，补偿后的控制对象C（z）P（z）在全频段位于0 dB线以下。因此可以得到：

图5 复合控制中函数特性曲线Fig.5 Function characteristic curve of hybrid control

由此可知满足 H（z）=|Q-C（z）P（z）|＜1的稳定性条件。

为进一步确定函数C（z）特性，对于超前环节zk中的k进行讨论分析。如图6所示，当k取不同值时，函数相频曲线不同。既要保证补偿后的受控对象在低频段无相移，同时高频段相移不应过大，因此取定k值为5。

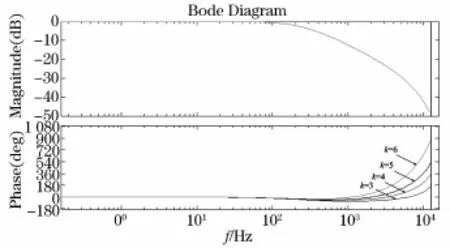
图6 k变化时 zk S（z）P（z）函数特性曲线Fig.6 Function characteristic curve of zk S（z）P（z）with varied k

由于实验中主要的谐波来源为电网电压，因此系统对于电网电压的工频谐波抑制能力至关重要。提高谐波抑制能力、改进电流波形质量也是加入重复控制的根本目的。因为Q不为1，因此系统存在稳态误差，可以根据谐波电压产生的稳态误差来分析不同控制方法的谐波抑制特性［15］。

将图4控制框图离散化可以得到误差信号ierr与谐波源us的关系，可以得到传统控制模式的谐波抑制特性：

同样，可以得到复合控制的谐波抑制特性：

显而易见，引入重复控制后，传递函数的分母多了一项GRC（z），因此系统跟踪误差减小，对于谐波抑制能力有所增强，增强的效果体现在GRC（z）上。

综上所述，与传统控制相比，复合控制具备较强的谐波抑制特性，使得电流跟踪的稳态误差更小，跟踪效果更好，有效减小了电流畸变程度。

4 仿真分析

为验证所提出谐波电压下新型控制方法的正确性和可行性，在Matlab/Simulink中搭建了三相四线制Vienna整流器基于传统控制和复合控制的仿真模型，通过对比两者控制效果，验证所提方案的优越性。同时也为实际的实验平台搭建提供仿真依据。系统仿真参数如表1所示。

表1 系统仿真参数Tab.1 Parameters of the simulation system

按照表中参数，首先搭建了系统仿真模型，分别基于三种情况进行了仿真：理想电网电压下、电网电压中加入谐波分量、电网电压塌陷。通过对比传统控制模式和复合控制模式下，两者电流跟踪的效果，最终得到复合控制方法在改善电流波形质量、抑制电流谐波方面的优越性。由于本文重点研究谐波电压下复合控制方法的跟踪效果，而理想电压与电压塌陷结果与之基本一致，因此本文仅列出谐波下的仿真结果。

4.1 谐波电压

在理想工频电网电压中加入3，5，7次谐波电压分量，有效值均为25 V，保证电压畸变率为20%左右。图7比较两种控制方法电流畸变程度，可以看出复合控制对于电流的谐波分量抑制效果更为明显，电流畸变更小，同样也能实现单位功率因数运行，同时直流侧波动也更小。

图7 两种方法在谐波电压下效果对比图Fig.7 Contrast charts of current tracking under harmonic voltage with two different methods

4.2 谐波畸变率

将三种工况下电流谐波畸变率汇总，得到表2，可以看出复合控制对于电流的谐波分量抑制效果更为明显，电流畸变更小。

表2 三种工况下谐波畸变率Tab.2 Total harmonic distortion under three working conditions

5 实验结果

为了验证所提出复合控制策略的有效性，搭建了三相四线制Vienna整流器的3 kW实验样机。实验装置主控制器采用DSP+FPGA的方式，实现全数字化控制。DSP作为系统的主控芯片实现数据处理和核心控制算法，FPGA完成数据的快速收发。实验采用Fluke电能质量分析仪与示波器记录数据。

5.1 理想电网电压

交流侧输入相电压为78 V，直流侧负载采用20 Ω，总运行功率为3 kW。当电网电压为理想电压时，如图8所示，通过比较传统控制与复合控制波形，可以得到各自的电流波形畸变率和功率因数。同时样机在40Ω—20Ω，与20Ω—40Ω两种负载切换模式下，均能正常工作。

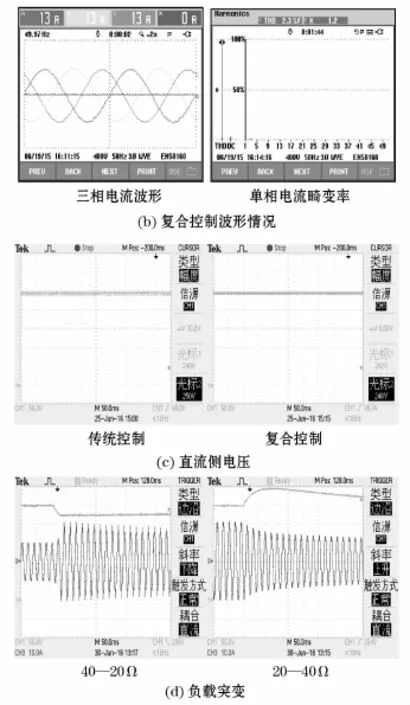
图8 两种方法对比效果图Fig.8 Contrast charts of working effects with two different methods

5.2 谐波电压

在Vienna整流器交流侧并联一个不控整流器作为谐波源，提供谐波电压。可以看出电压波形发生明显畸变，其中含有一定含量的5，7次谐波，谐波畸变率为8.3%。如图9所示，此时对比传统控制与复合控制的电流波形质量，可以得到复合控制跟踪精度更好。

图9 两种方法抑制谐波效果对比图Fig.9 Contrast charts of restraining harmonic with two different methods

6 结束语

以三相四线制Vienna整流器的拓扑结构为基础，基于单相解耦模式，实现了功率因数校正。主要针对电网电压受到干扰的情况，提出了针对谐波的改进电流跟踪方法。同时对电流环加以改进，引入重复控制与PI控制并联的复合控制方法，对复合控制器的参数设计与谐波抑制特性进行了充分的理论分析，通过对比传统控制方法与复合控制的不同，验证了所提方案的有效性。最终实验表明，复合控制方案拥有更好的谐波抑制特性，有效地降低了电网电流的畸变程度，波形质量有了明显的提高。同时也能减小直流侧电压波动，使得直流输出更稳定。