基于GA-PS的轨道橡胶隔振器滞回模型参数识别

， ，

(1.石家庄铁道大学 土木工程学院，河北 石家庄 050043；2.石家庄铁道大学 机械工程学院，河北 石家庄 050043)

基于GA-PS的轨道橡胶隔振器滞回模型参数识别

刘伟栋1，廖英英1，刘永强2

(1.石家庄铁道大学 土木工程学院，河北 石家庄 050043；2.石家庄铁道大学 机械工程学院，河北 石家庄 050043)

针对一种新型可便捷检修和更换的浮置板用隔振器中的橡胶结构元件进行力学性能试验，得到了不同幅值和频率激励下位移-力滞回特性曲线。采用一种半物理模型Bouc-Wen模型来模拟橡胶滞回特性，利用一种新型的参数识别方法GA-PS法对模型中的未知参数进行识别，得到了可以很好模拟橡胶滞回特性的数学模型，并进行了验证。结果表明：不同的幅值和频率激励下，Bouc-Wen模型的仿真滞回曲线和实验测量滞回曲线吻合良好，验证了GA-PS识别方法在橡胶隔振器参数识别中的有效性与准确性。这种参数识别方法可以精确地识别出可以模拟橡胶特性的滞回曲线的参数，为模型的后续应用打下了基础。

浮置板；隔振器；滞回曲线；参数识别；Simulink

0 引言

日新月异的今天，轨道交通给人们带来便利的同时噪声带来的不利影响愈加严重，减振降噪成为轨道交通领域中一个不可回避的课题。经过研究和实际列车运行实践比较，浮置板减振效果明显，减振效果是各种减振措施中最好的[1-5]。浮置板的减振器系统主要有两种：橡胶制品和钢弹簧制品。两者在施工工艺、产品更换和设计计算上大致基本相同，但由于橡胶减振器的价格低三分之二而为其一大优势[6]。当浮置板质量相同时，橡胶减振器制作的浮置板和钢弹簧的垂向固有频率差别甚微。钢弹簧在防腐和抗老化的性能上不及橡胶[7-8]。在降低振动要求来说，需要减振器具有三向刚度，橡胶本身的特性很容易调整到要求刚度，但是钢弹簧却很难达到要求。本文采用的是新型轨道交通浮置板用减振器的橡胶元件，此新型隔振器具有很大的纵横向刚度，最大的优势在于安装和更换方便，限位器也可不再使用。对这种新型的隔振器橡胶元件进行试验，得到可表示橡胶特性的滞回曲线，选择Bouc-Wen模型模拟橡胶滞回曲线，并用一种新型的参数识别方法GA-PS法[9]进行参数识别获取其中的位置参量，分析并处理数据获得了其力学特性的参数。

图1 橡胶试件

1 橡胶试件实验

实验用橡胶试件尺寸，外径：R=225 mm，内径：r=45 mm，厚度：h=60 mm。如图1所示。

图2 MTS试验机

为了确保实验的真实可靠性，实验步骤的制定根据振动与冲击隔离器性能测试方法国家标准GB/T 15168—94。橡胶试件在25±5 ℃环境中存放4～6 h后，在此环境中进行性能测试。确保所有测试仪器、设备、仪表全部都符合GB5170要求。实验采用的实验仪器为石家庄铁道大学交通环境与安全工程研究所的MTS试验机，如图2所示。试验机最大的试验荷载为±250 kN，实验频率范围可以达到0.001～50 Hz，最大的工作空间为1 625 mm，可控变量有力、位移、应变。此试验机为美国产的，精度较高，采集数据灵敏。

对橡胶试件进行正弦加载，首先进行预载27 kN，排除由于实验仪器和试件接触不良好造成的误差。加载频率分别为：6 Hz,7 Hz,8 Hz,9 Hz,10 Hz,13 Hz，加载幅值分别为：0.8 mm，1.0 mm，1.2 mm，1.4 mm，1.6 mm。在保证全周期的滞回图形对的前提下，选取一定数量的控制点绘制得到完整的滞回曲线。首先采用幅值为1.6 mm、频率为 8 Hz 的试验数据进行参数识别，再用其他幅值和频率的试验数据进行验证。

2 模型参数识别方法

2.1 遗传算法

Holland教授在1962年提出了遗传算法Genetic Algorithm。遗传算法的计算首先从一个个体数量一定的原始的种群开始，但染色体的特征各异，然后在反复修改群体的同时随机选择一组个体作为父本产生子代。最后经过连续的遗传修正逐渐走向群组的最优化解。遗传算法优点是可以解决其他的一些标准优化算法无法解决的问题，比如目标函数为不连续、不可微的、具有随机性或很强的非线性特性。遗传算法每次用 3种主要类型的方法产生下一代[10-12]。本文中滞回函数为非线性约束问题，主要采用扩大化的拉格朗日遗传算法(Augmented Lagrangian Genetic Algorithm, ALGA)进行，算法为

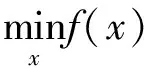
约束为

ci(x)≤0,i=1…mceqi(x)=0,i=m+1…mt
A·x≤b
Aeq·x=beq
lb≤x≤ub

(1)

式中，ci(x)为非线性不等式约束函数，个数为m；ceqi(x)为非线性等式约束函数；mt为非线性约束的总个数；Aeq,beq为线性等式约束系数；A,b,lb,ub为线性不等式约束系数。

利用Matlab进行计算的表述为

遗传算法它的全局搜索能力较强，能在较为宽泛的范围内快速识别到需要的解。但是遗传算法的缺点也很明显，很容易识别失败，在未获得最优解之前就收敛，此时得到的解不具有全局性而仅仅是局部的。

2.2 模式搜索法

模式搜索法Pattern Search是一种直接搜索算法，其目标函数不一定可微也可能是非连续。模式搜索法优点是可以快速地得到全局的最优解。模式搜索法的计算首先在已知节点的附近分布一个包括一系列的点的网格结构，它由已知的节点进行矢量计算得出的，矢量计算中的那些向量被称之为模式。在计算中如果在这些网格中发现了一个比当前目标函数更小的点，就会用这个点来取代本次计算的点，用于下一次的计算，以此类推直到找到了最优的解[13]。

利用Matlab进行计算的表述为

式中，@objfun为目标函数的句柄；x0为算法初始节点；x为算法得到的最终节点；fval为算法得到的最终目标函数值。

用模式搜索法进行计算，类似于遗传算法可以进行线性以及非线性的约束计算。尽管模式搜索法的计算效率高速度快，但是它的缺点在于过度地依赖初值，仅仅单独使用的时候效果不是很好。

2.3 GA-PS搜索法

综述分析可知：遗传算法的全局搜索能力较强但是局部的识别能力较差；模式搜索法计算速度快，在给定优良的初始值可以得到局部的最优解。单独使用遗传算法的时候因其易收殓，不一定能得到最精确的解，可能是全局的一个解。但此值具有全局最优性，可以满足模式搜索法对于初始值的依赖，可快速地识别得到最优局部解。这种联合方法既考虑了遗传算法的易失败性也考虑了模式搜索法的初始值依赖性，充分利用二者的优势，快速地得到参数识别所需要的最优解。

3 Bouc-Wen 模型

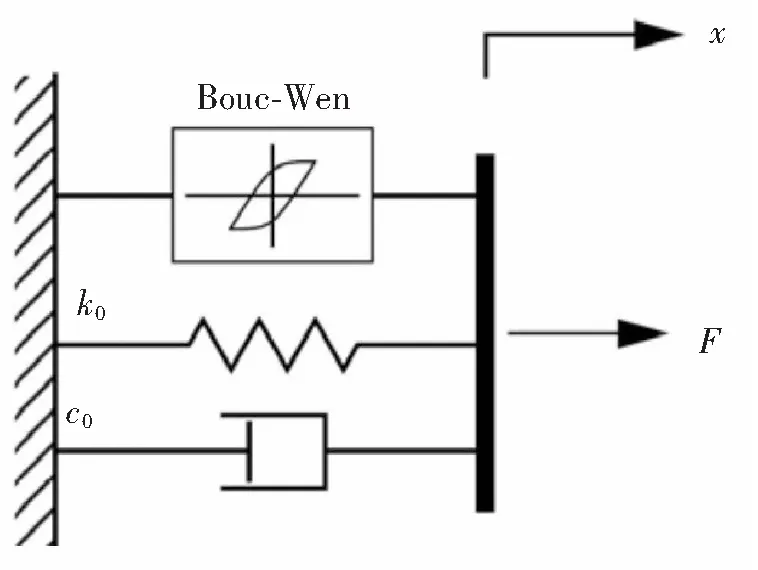
图3 Bouc-Wen 模型

对于橡胶滞回特性的问题，橡胶本构模型有: Mooney-Rivlin、Bouc-Wen 模型、Polynomial及 Prony 模型等。考虑模型的适用性，本文采用Bouc-Wen 模型进行橡胶滞回曲线的参数识别。Bouc-Wen 模型能够很好地模拟橡胶滞回的特性，通用性特别强，便于数据的处理。Bouc-Wen 模型如图3所示。

Bouc-Wen力学模型为

目标函数

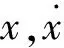
此目标函数值的意义可以表示为仿真值和试验值的误差率，误差率越小仿真的吻合率越大，用100%减去误差率可以得到识别结果的吻合率。由以上公式可以看出，共有8个待识别参数：c0、k0、x0、α、β、γ、n、A。Bouc-Wen 模型的Simulink程序如图4所示。

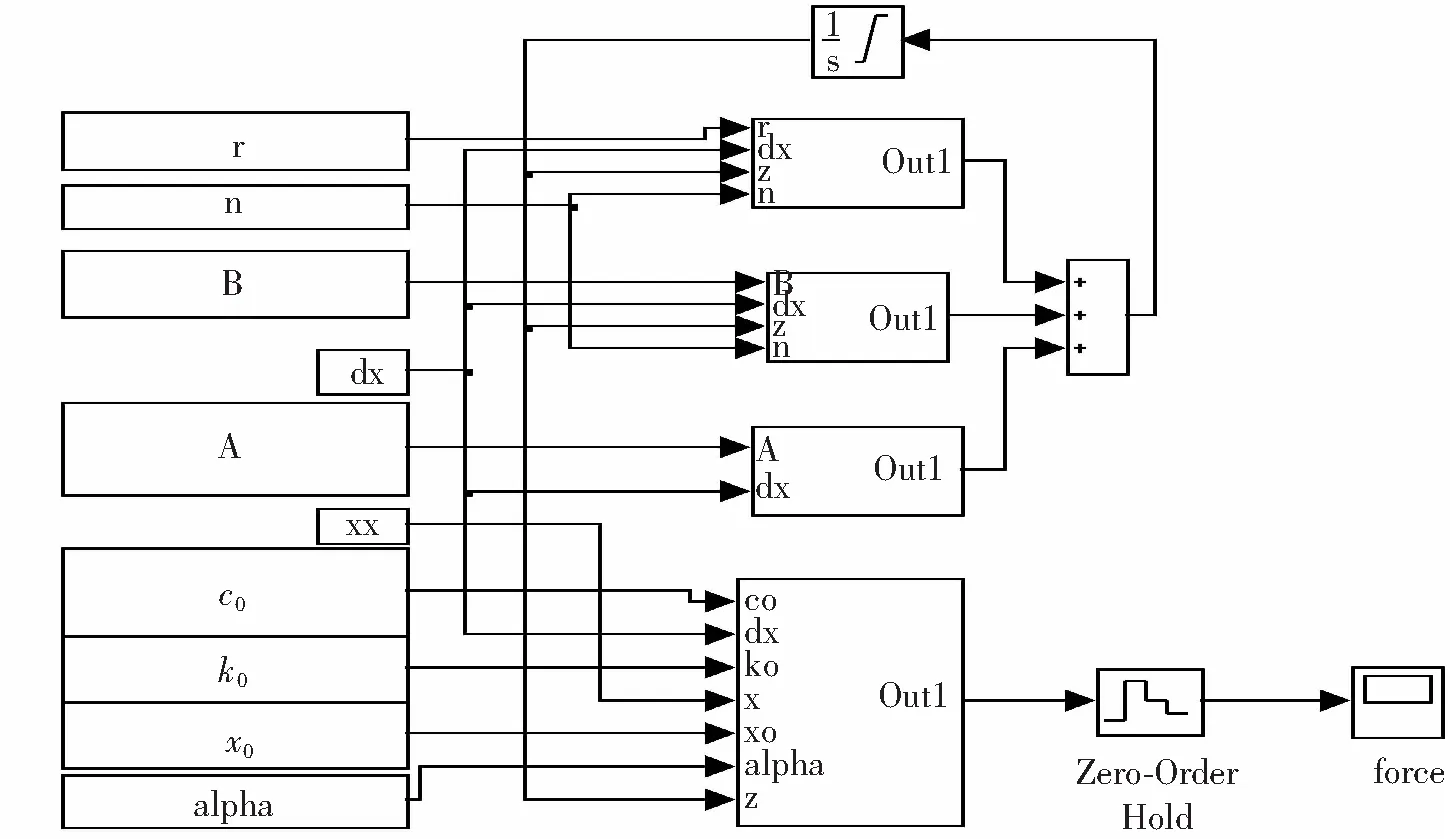
图4 Simulink程序图

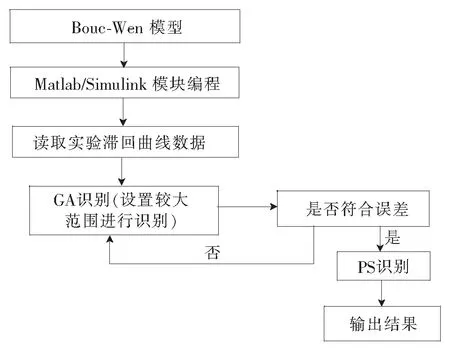
图5 参数识别流程图

4 参数识别

参数识别流程如图5所示。

利用频率为8 Hz，幅值为1.6 mm的实验数据作为识别数据进行识别，采用其他幅值和频率数据进行验证。Simulink中设置GA-PS识别的控制参数：采用初始群体个数为N=50 ；选择算法采用随机均匀分布选择；交叉采用分散交叉的方法，交叉概率取 0.8；变异采用高斯函数方法，生成服从高斯分布、均值为 0 的随机数加到父代上，尺度取 0.5，压缩取 0.7，进行1 000代运算。PS识别运算进行500次运算。识别结果为：alpha=1.863，c0=7.236，k0=6 463.996，r=2.062，B=-6.099，A=12.360，n=0.797，x0=-0.028，fval=0.0137。吻合率为98.63%。识别Bouc-Wen 模型结果为

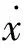
(7)

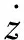
(8)

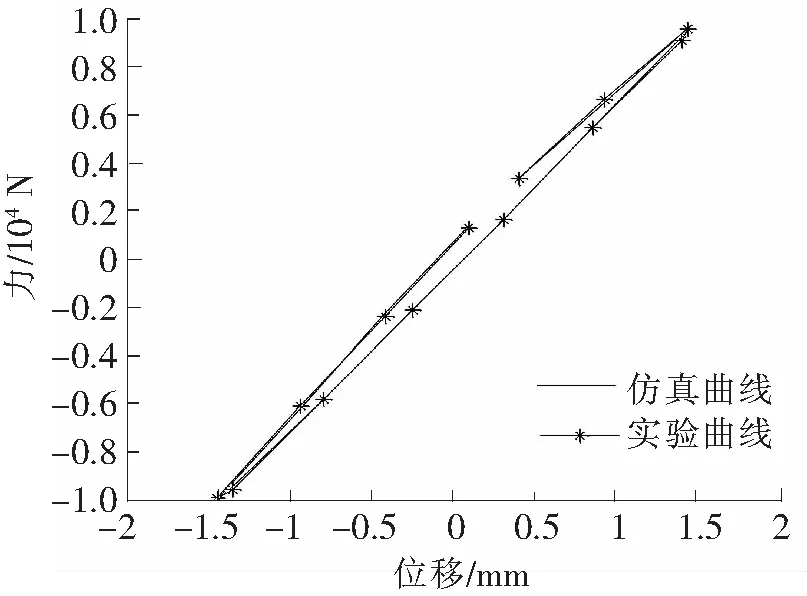
图6 1.6 mm 8 Hz实验与仿真对比图

5 结果分析

5.1 识别结果分析

为了确定此方法识别的参数的可靠性，现代入频率为8 Hz、幅值1.6 mm的原始数据到所识别出来的Bouc-Wen 模型里面得到位移-力的滞回曲线并和原始实验得到的滞回曲线进行对比分析，如图6所示。

由图像对比可知： 频率为8 Hz，幅值为1.6 mm时实验滞回曲线和仿真滞回曲线吻合非常好，很好地证明了GA-PS识别方法的初步有效性。

5.2 识别结果验证

上节已经提到频率为8 Hz，幅值为1.6 mm为参数识别数据识别出来的8个未知参量的初步有效性，为了进一步的验证此方法的正确性以及精确性，利用其他实验数据验证。识别结果对比如图7～图10所示。

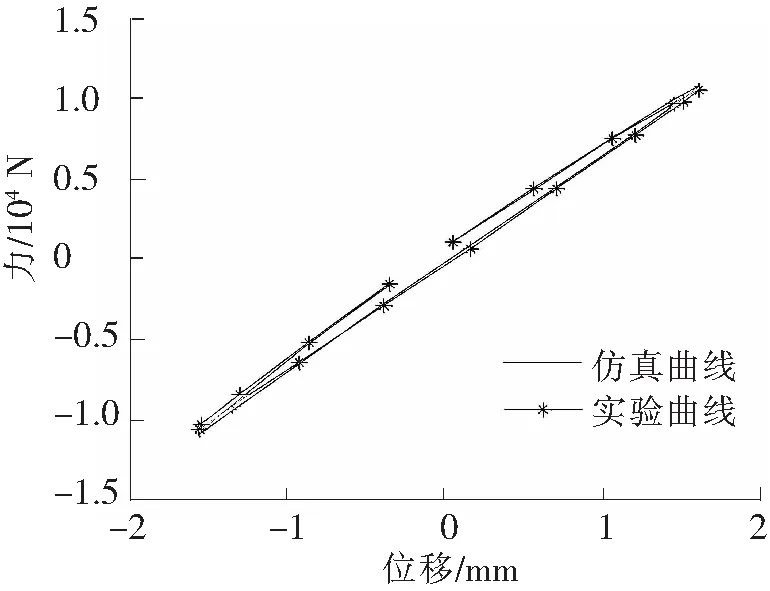
图7 1.6 mm 6 Hz实验与仿真对比图

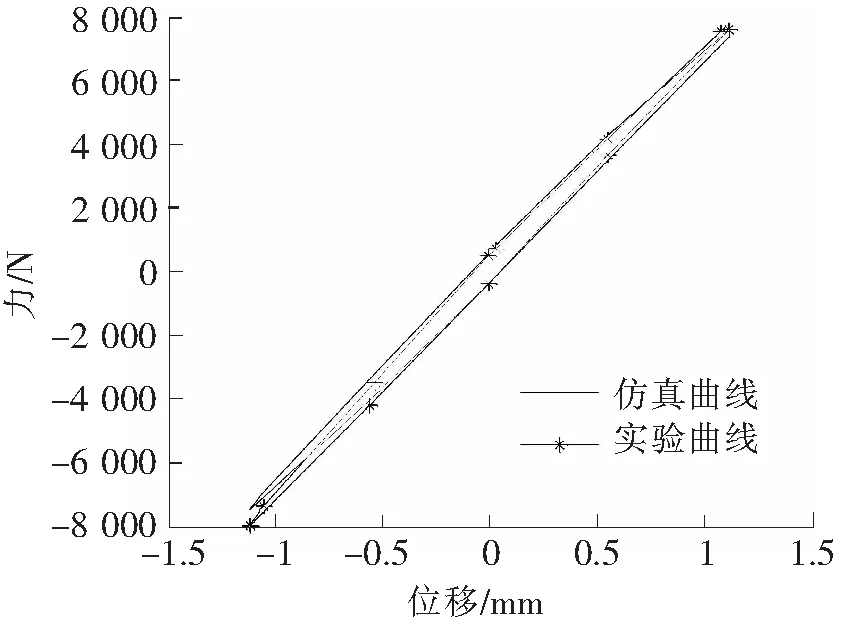
图8 1.6 mm 10 Hz实验与仿真对比图

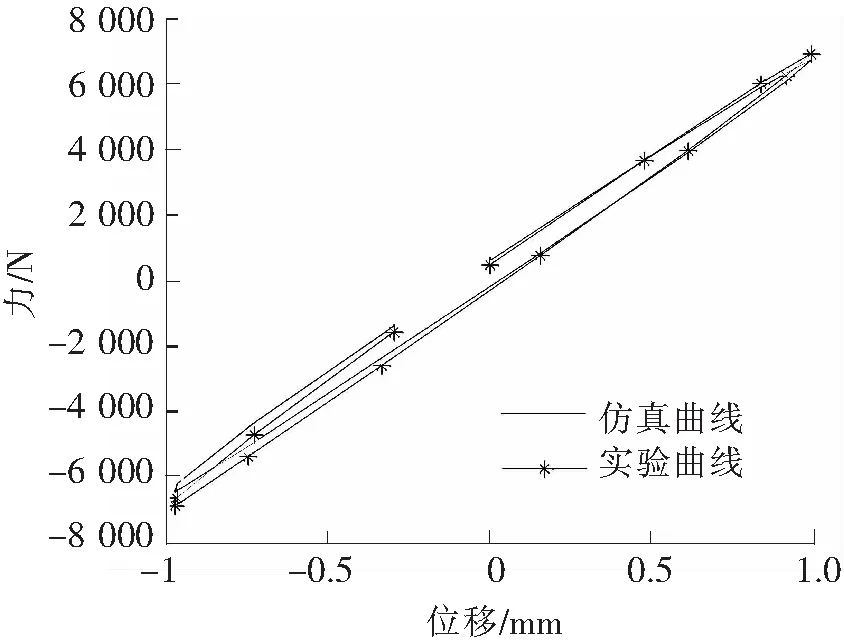
图9 1.0 mm 8 Hz实验与仿真对比图

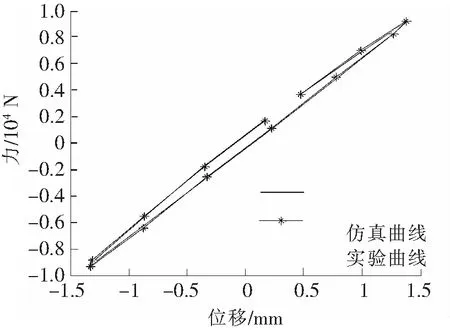
图10 1.4 mm 8 Hz实验与仿真对比图

图7～图10为部分不同的频率和幅值下原始实验图像与识别后的图像对比图。其他频率和幅值的组合对比吻合性良好。通过对比图显示，不同的幅值和频率下，Bouc-Wen模型识别滞回曲线和实验测量滞回曲线吻合良好。

6 结论

通过对新型减振器橡胶元件的实验得到不同幅值和频率橡胶滞回曲线，并选择Bouc-Wen模型模拟橡胶滞回曲线，用一种新型的参数识别方法GA-PS法进行参数识别获取未知参数。识别出的未知参量带入到模型当中，进行实验和仿真的对比验证。

主要结论如下：

(1)以频率为8 Hz，幅值为1.6 mm作为识别原始数据下识别出的参数值符合Bouc-Wen模型各项参数的取值范围，并且原始数据绘制的图像与仿真图像吻合度良好，可以达到98.63%。

(2)以频率为8 Hz，幅值为1.6 mm作为识别原始数据下识别出的参数值代入到Bouc-Wen模型中，同时分别验证其他频率和幅值，对比图结果表明不同幅值和频率下实验与仿真结果吻合度良好。

(3)GA-PS识别法对橡胶元件滞回模型进行参数识别有效性好，识别精度高，其结果可以作为有限元仿真的基础应用。

[1]刘海涛,王继军,赵勇,等.城市用减振型无砟轨道的研发[J].铁道建筑,2016,56(1):59-62.

[2]李建斌.城市轨道交通轨道减振降噪设计研究[J].石家庄铁道大学学报：自然科学版,2011,24(1):73-77.

[3]义涛.城市轨道交通减振降噪分析及工程措施[J].铁道工程学报,2010,27(2):85-88.

[4]颜华,姚力.浮置板轨道设计[J].铁道工程学报,2002,19(4):12-15+11.

[5]杨绍普,郭亚娟.浮置板道床非线性动力特性分析[J].振动与冲击,2006,25(2):51-54+183-184.

[6]姚京川,杨宜谦,孙宁.浮置板式轨道结构的发展[J].中国铁路,2003,42(7):20-22+10.

[7]徐志强,姚京川,杨宜谦,等.橡胶支承浮置板式轨道结构动力计算分析[J].铁道标准设计,2003,47(8):11-13.

[8]林松,张鲲,孙磊,王旭,等.橡胶隔振器动态特性的本构研究[J].振动与冲击,2011,30(3):177-179+210.

[9]刘永强.基于磁流变阻尼器的高速动车组半主动控制与时滞分析[D].北京:北京交通大学机械电子与控制工程学院,2011.

[10]边霞,米良.遗传算法理论及其应用研究进展[J].计算机应用研究,2010,27(7):2425-2429+2434.

[11]葛继科,邱玉辉,吴春明,等.遗传算法研究综述[J].计算机应用研究,2008,25(10):2911-2916.

[12]李伟,王轲,朱德懋,等.基于遗传算法的非线性迟滞系统参数识别[J].振动与冲击,2000,19(1):10-13+90.

[13]黄天云.约束优化模式搜索法研究进展[J].计算机学报,2008,30(7):1200-1215.

ParameterIdentifyingoftheRubberDamperHysteresisLoopBasedonGA-PS

LiuWeidong1,LiaoYingying1,LiuYongqiang2

(1.School of Civil Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China; 2.School of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China)

An experiment is conducted pointing at the rubber isolator used on a new type of track floating slab which is easy to repair and replace,and then the displacement force hysteresis characteristic curves are obtained under different amplitude and frequency excitation. Using a semi physical model, Bouc-Wen model, the hysteretic characteristics of rubber is simulated. By using a new type of parameter identification method, the unknown parameters of the model are identified.The results show that the simulated hysteresis curves are in good agreement with the curves which are measured by experiment under different amplitude and frequency excitation, which verifies the efficiency and accuracy of the GA-PS in parameter identification of rubber isolator. The method of parameter identification can identify parameters of hysteresis loops which can imitate characteristic of rubber accurately,and lay the foundation for high-precision model of finite element analysis.

floating slab;vibration isolator;hysteresis loop;parameter identifying;simulink

U214.5

A

2095-0373(2017)04-0046-06

2016-08-31责任编辑车轩玉

10.13319/j.cnki.sjztddxxbzrb.2017.04.09

国家自然科学基金(11227201;11202141; 11302137; 11472179;11572206;11372199)、河北省自然科学基(A2013210013; A2015210005)、河北省教育厅项目(YQ2014028)

刘伟栋(1991-),男，硕士研究生，研究方向：轨道减振降噪。E-mail：379894497@qq.com

刘伟栋，廖英英，刘永强.基于GA-PS的轨道橡胶隔振器滞回模型参数识别[J].石家庄铁道大学学报:自然科学版,2017,30(4):46-51.