自锚式预应力混凝土矮塔斜拉桥的力学极限跨径研究

, ， ，

(1.天门市建设工程质量监督站, 湖北 天门 431700；2.中交第二航务工程局有限公司技术中心，湖北 武汉 430040)

自锚式预应力混凝土矮塔斜拉桥的力学极限跨径研究

彭义1,宋涛2，盛曼1，江姣1

(1.天门市建设工程质量监督站, 湖北 天门 431700；2.中交第二航务工程局有限公司技术中心，湖北 武汉 430040)

从主梁竖向挠度及应力、拉索强度、屈曲稳定性、抗风稳定性等的5个方面探讨了基于当前技术条件下的自锚式预应力混凝土矮塔斜拉桥的极限跨径。研究表明：屈曲稳定性是限制矮塔斜拉桥跨径增大的决定性因素，恒活载作用下的主梁应力居次要地位，而主梁挠度、拉索强度及结构抗风稳定性对该结构体系的极限跨径影响很小。预应力混凝土矮塔斜拉桥极限跨径的突破首先要解决该结构体系的屈曲稳定性问题。该研究成果可用于双塔塔梁固结、墩支承体系的矮塔斜拉桥的初步概念设计阶段选择合理的结构参数。

桥梁工程；矮塔斜拉桥；极限跨径；屈曲稳定性

0 研究背景

苏通长江大桥和昂船洲大桥的建成以及正在建设的沪通长江大桥引领着现代斜拉桥向千米级发展。自从上世纪70年代起，很多学者就开展了基于力学的斜拉体系极限跨径的研究，但是随着材料科学和计算手段的发展，极限跨径到底是多少，到现在还是未知。Gimsing[1]从拉索竖向支承效率角度，推算出斜拉体系的极限跨径是5 000 m;李国豪[2]从拉索弹性模量非线性角度提出斜拉体系的极限跨径是3 600 m；瑞士Miler[3]认为钢桥的极限跨径是5 000～7 000 m，采用CFRP材料，其极限跨径为15 000 m；法国J.Muller[4]认为如果采用“双锚体系”可将斜拉体系的极限跨径做到3 000 m；德国R.Saul[5]对2 000 m左右的斜拉体系和悬索体系做了全面分析后，认为斜拉桥在经济性能上更为经济。Gimsing[1]曾提出过一个大胆的设想：在斜拉体系中若综合运用双锚体系、空间拉索体系及新型材料等可将斜拉体系的极限跨径做到20 000 m,因此对于主跨采用15 000 m的斜拉体系直接跨越直布罗海峡，无需中间修筑基础。目前，已建成的大跨矮塔斜拉桥均采用常规的双塔三跨全自锚式结构体系、双索面布置，如大连长山大桥(主跨为260 m)及正在建设主梁采用钢桁架的芜湖长江公铁二桥(主跨为588 m)[6]。在当前技术条件下，开展该体系的极限跨径的研究，有重要的现实意义，但是目前暂时未见相关文献报道。本文将从主梁挠度及应力、斜拉索强度、屈曲稳定性、抗风稳定性等方面展开此研究。

1 活载作用下的主梁竖向挠度

主梁在恒载作用下的挠度可通过设置预抛高来消除，下面仅讨论主梁在活载作用下的挠度。将主梁等效为多跨弹性支承连续梁，其竖向挠度计算表达式为

式中，P为作用于跨中的集中荷载；p为均布荷载；L为特征长度；K为地基系数。

为简化计算，假设边中跨比为0.5，则由式(1)可得

将式(2)代入式(1)可得

式中，k为高跨比；Lc为主跨跨度。

结构计算参数取值如下：大跨度斜拉体系一般采用双向3车道或4车道布置，可按照《公路桥涵设计通用规范》[7]确定活载集度p，若按照双向4车道布置，车道纵向折减系数为0.97，车道横向折减系数为0.5，偏载系数为1.15，则活载集度为p=46.85×103N/m。考虑到重车作用，将活载集度放大1.5倍，则活载集度为1.5×46.85×103=70.28×103N/m。因此，本计算中车道荷载中的均布荷载取为7.0×104N/m。车道荷载中的集中荷载取为P=161×104N/m，拉索和主梁的弹性模量分别取为1.95×105MPa,3.6×104MPa,主梁抗弯惯矩为50 m4。

主梁主跨跨径与最大竖向挠度之间的关系如图1所示。由图1分析知，在活载作用下主梁的竖向挠度随主跨跨径迅速增大。竖向挠度随梁上索距增大而增大；随高跨比增大而减小。如梁上索距为4 m，高跨比为0.1时，此时主梁的竖向挠度值不作为矮塔斜拉桥的极限跨径的限制条件，在考虑经济性能的前提下[8]，矮塔斜拉桥的极限跨径为500 m，因此在概念设计阶段选取合理的主梁显得尤为重要。

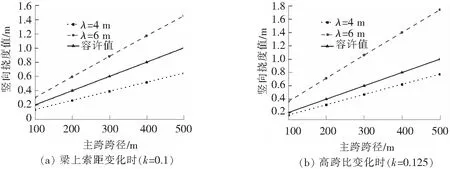
图1 主跨跨径与竖向最大挠度之间的关系

由此分析可知，影响矮塔斜拉桥在活载作用下竖向挠度的因素有以下方面：索塔高度与主梁主跨之比(即高跨比)、拉索在主梁上的布置间距、主跨跨径及拉索的弹性模量等。增加主梁的高度及高跨比、减小主梁上的索距都可达到减小主梁竖向挠度的目的。在上述诸多因素中，其中高跨比能够显著影响主梁在活载作用下的挠度。

2 恒、活载组合作用下的主梁应力

靠近桥塔处的主梁在恒、活载作用下承受着较大轴力，其成为限制斜拉体系的极限跨径进一步增大的因素。靠近桥塔处主梁的轴力近似表达式为

可得

式中，ηA为靠近主塔截面的主梁截面增大系数；A0,Ag,[σ],γg为主梁靠近主塔截面的截面面积、平均面积、容许应力及容重；ηg为考虑主梁构造等主梁容重增大系数；g,p分别为作用主梁的恒活载；g2为二期恒载。

计算参数取值如下：活载p及二期恒载g2取值为7×104N/m；混凝土主梁容重γg取值为2.65×104N/m；Ag主梁截面取值为50 m2；C60混凝土的容许应力为26.5 MPa。矮塔斜拉桥极限跨径与主梁平均截面之间的关系如图2所示。由图2分析可知，主跨极限跨径随主梁截面增大而增大；在主梁截面积一定条件下，主跨极限跨径随拉索在梁塔上的索距比及索塔高跨比增大而增大。但是在主梁截面面积在30～50 m2范围内，主跨极限跨径随主梁面积增大而较其他面积增大较快。当主梁截面面积为50 m2，梁塔索距比为6，索塔高跨比为0.1，容许压应力为26.5 MPa,此时极限跨径仅为479 m。

上述计算过程并未计入恒活载引起弯矩对主梁的作用，如计入弯矩引起的弯曲应力，则主梁的轴向压应力将会降低。为研究方便，将主梁的容许应力乘以0.8的折减系数，在同等条件下，此时的极限跨径仅为383 m。

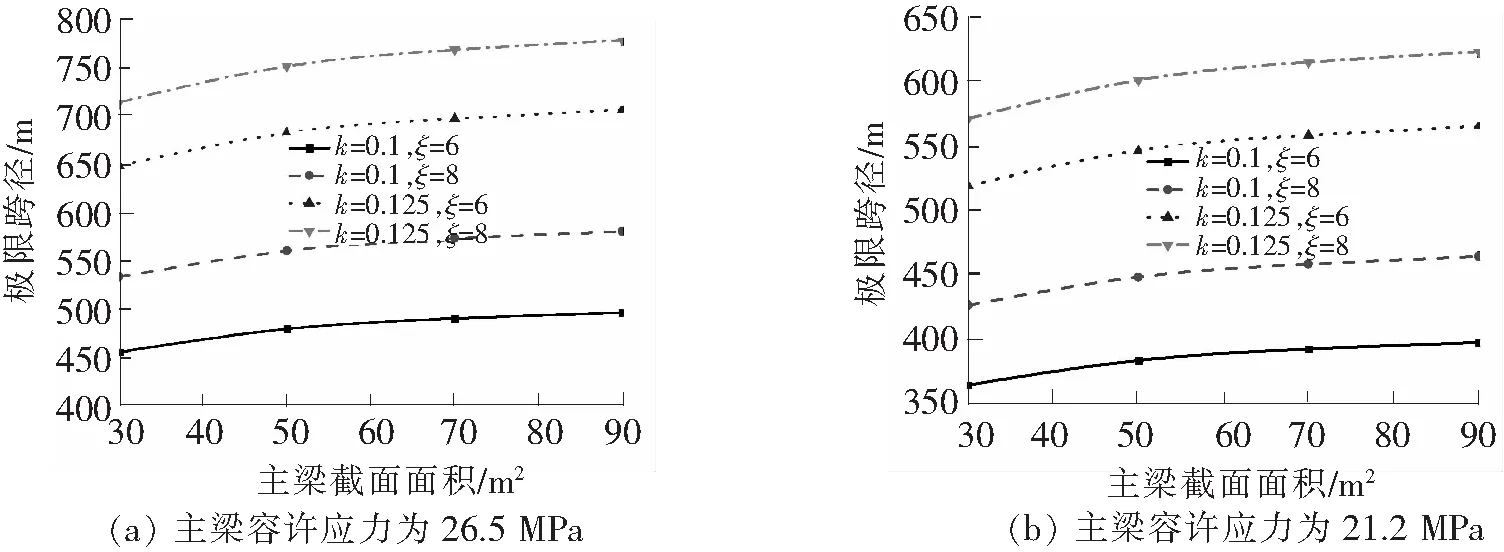
图2 主跨跨径与主梁平均面积之间的关系

3 斜拉索强度

在斜拉体系中受力最不利的拉索是靠近跨中的最长斜拉索。随着主跨跨径的增大，拉索长度必将随着增大，从而导致拉索竖向支承效率降低。现在计入垂度效应情况下，探讨矮塔斜拉体系的拉索强度对主跨极限跨径的影响。

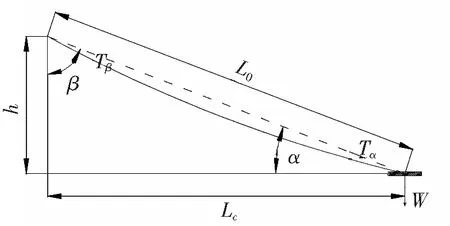
图3 斜拉索受力示意图

《公路斜拉桥设计细则》[9]规定，在斜拉桥计算中必须考虑拉索的垂度效应，并指出可采用抛物线索单元考虑拉索的垂度效应具有足够的计算精度。

由图3分析可知，存在如下关系表达式

式中，Tα,Tβ分别为拉索梁端及塔端的索力;H为拉索索力在梁端的的水平分力。

计入拉索垂度效应后，索塔高跨比与极限跨径的关系如图4所示。由图4分析可知，主跨极限跨径随梁上索距减小而增大；随高跨比增大而增大；随恒载集度增大而减小。当恒载集度为g=5.0×105N/m，高跨比为0.1，梁上索距为4 m，计入经济性能的因素，此时矮塔斜拉桥的极限跨径为500 m。

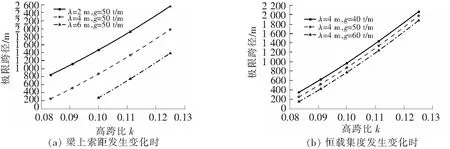
图4 索塔高跨比与极限跨径的关系

计入拉索的垂度效应后，随拉索的长度增加，拉索梁端的水平倾角进一步减小，从而使得拉索竖向支承效率减小。对于计入垂度后的拉索，定义其竖向支承承载效率为

式中，θe为拉索竖向支承承载效率；V0,V1分别为计入拉索垂度效应前后的拉索梁端索力的竖向分量。

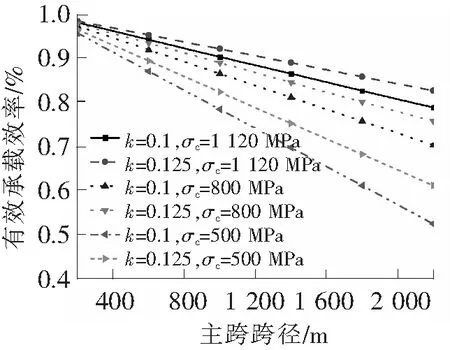
图5 主跨跨径与拉索有效承载效率的关系

本文为研究主跨跨径与计入拉索垂度效应后的有效竖向承载效率，特将主跨跨径适当放大。主跨跨径与拉索有效竖向承载效率的关系如图5所示。由图5分析可知，拉索竖向支承效率随主跨跨径增大而迅速减小；当主跨跨径确定时，拉索竖向有效支承效率随结构高跨比及拉索截面的应力增大而增大。

拉索强度限制主跨跨径进一步增大主要有以下因素：索塔高跨比、主梁恒载集度及梁上拉索布置间距等。当拉索抗拉强度极限确定，可采取增大高跨比、减小梁上恒载集度及索距等措施，达到发挥主梁极限跨径的目的。如采用GFRP筋做成斜拉索，则是提高极限跨径的一种措施。

4 屈曲稳定性

随着主跨跨径的不断增大，斜拉体系的失稳模态由桥塔控制转变为主梁屈曲或索梁塔耦合失稳等。在恒活载作用下的主梁将承受较大的轴向压力，易发生面内屈曲失稳；若主梁横向抗弯刚度不足，则其发生面外失稳。本文将主梁等效为两端铰接的弹性地基梁，其弹性支承刚度K采用lc/4处的地基系数，其面内屈曲稳定性按式(10)计算，其表达式为

式中，Ncr为面内屈曲临界压力；K(lc/4)为lc/4处的弹性地基系数，lc/4处的弹性地基系数按照式(11)计算；N(lc/4)为lc/4处的轴力，按照式(12)计算。

结构计算参数取值如下：恒载分别取5×105N/m,8×105N/m，主梁竖向抗弯惯性矩分别取为50 m4，40 m4，横向抗弯惯性矩分别2 000 m4,1 000 m4。

矮塔斜拉桥一阶弹性稳定系数与主跨跨径之间的关系如图6所示。由图6分析可知，一阶弹性稳定系数随主跨跨径增大而减小，尤其是一阶面外稳定系数降低更为显著。从另一个角度分析可知，要求在设计主梁时要注意结构稳定性控制由面内转为面外失稳控制。若规定失稳系数不小于4，竖向和横向抗弯惯性矩分别取为50 m4，2 000 m4,恒载取为5×105N/m。此时结构的极限跨径由一阶面内稳定性控制，其极限跨径为306 m。

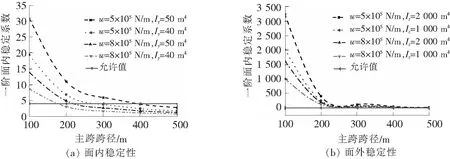
图6 主梁弹性稳定与主跨跨径的关系

由此分析可知，影响主梁屈曲稳定性的因素主要有主梁抗弯惯矩、恒活载荷载集度等因素，如要提高结构的稳定性尽可能减小恒载集度，从而有效提高结构的弹性稳定性。

5 抗风稳定性

矮塔斜拉桥一般修建峡谷或水道等风力作用较为明显的地方，因此在设计过程中需要考虑桥梁抗风问题。《公路桥梁抗风设计规范》[10]规定斜拉体系需进行抗风稳定性验算。

斜拉体系的抗风稳定性验算主要包括：颤振稳定性、驰振稳定性及静力稳定性。目前，大跨及超大跨斜拉体系抗风稳定性研究重点在于结构的颤振稳定性，但是有的学者研究指出，静力失稳可能在大跨或超大跨斜拉体系中率先发生，并在一些实验中得到证实。静力失稳研究不够深入，规范[10]给出的估算公式误差出入较大，一般采用风洞实验加以验证。下面仅就颤振稳定性，讨论矮塔斜拉体系的极限跨径。由近似计算公式可知

式中，ηs为形状系数；ηa为攻角效应系数；ft为扭转基频；B为桥面全宽，B=2b；μf为风速脉动修正系数；Vd为设计基准风速；m为桥面系主缆单位长度质量。

由《公路斜拉桥抗风设计规范》[10]5.2.2条，对双塔斜拉桥的扭转基频可按式(14)估算

式中，C为扭转基频常数。

由式(13)、式(14)可得

结构计算参数取值如下：C=14；主梁截面形状截面系数ηs=0.90；风攻角效应系数ηa=0.90；空气密度ρ=1.25；风速脉动修正系数μf=1.20；设计基准风速Vd=400 m/s；主梁高宽比H/B=5/36。

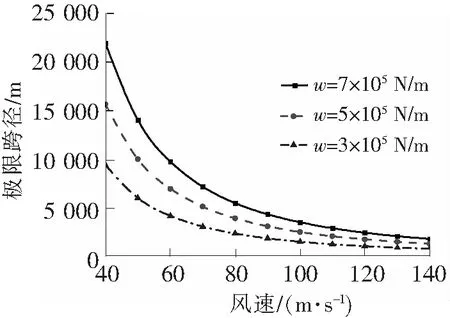
图7 设计基准风速与极限跨径的关系

矮塔斜拉桥极限跨径与设计基准风速的关系如图7所示。由图7分析可知，矮塔斜拉桥的极限跨径对设计基准风速增大而迅速减小而随桥面系质量增大而增大。当设计风速为40 m/s，桥面系每延米质量为5×105N/m，同时在计入经济性能的前提下，此时矮塔斜拉桥极限跨径为500 m。

由此分析可知，影响矮塔斜拉体系的抗风稳定性主要有以下因素：主梁自重及截面特性、设计基准风速等。若要提高结构的抗风稳定性可通过以下措施：增大主梁的单位长度质量；改变主梁截面形式；提高结构的扭转基频等。

6 结论

从主梁挠度及应力、拉索强度、结构屈曲及抗风稳定性等方面探讨了矮塔斜拉桥的极限跨径。为方便比较，将受各因素限制的矮塔斜拉桥的极限跨径列于表1中。

表1 自锚式预应力混凝土矮塔斜拉桥极限跨径

由以上研究结果，可得出以下结论：

(1)结构屈曲稳定性是限制矮塔斜拉桥跨径增大的决定性因素；恒活载作用下的主梁应力居次要地位，而主梁挠度、拉索强度及结构抗风稳定性对该结构体系的极限跨径影响很小。

(2)限制矮塔斜拉桥主跨跨径进一步增大的两个因素均与主梁恒载集度有关。对于预应力混凝土矮塔斜拉桥，在设计工作中应尽可能采用质轻高强的高性能混凝土，以达到实现进一步增大主跨跨径的目的。

[1]Gimsing N J, Georgakis CT. Cable Supported Bridges[M]. Chichester: John Wiley& Sons Ltd.,2012.

[2]李国豪.大跨桥梁发展概略[R].上海:同济大学,1987:1-10.

[3]Miler U．Structural tensile elements made of advanced composite materials [J]．Structural Engineering International,1999, 99(4):281-285.

[4]Muller J M.Very Long Span Bridges: Concepts, Materials and Methods [R].Kobe: IABSE,1998: 34-48．

[5]R Saul,林广元.特大跨度斜拉桥[J].世界桥梁,1991(3):78-79.

[6]宋涛.矮塔斜拉桥近似分析方法研究[D].西安:长安大学,2016.

[7]中华人民共和国交通部. JTG D60-2015公路桥涵设计通用规范[S].北京:人民交通出版社,2015.

[8]陈从春.矮塔斜拉桥设计理论核心问题研究[D].上海:同济大学,2006.

[9]重庆交通科研设计院.JTG D65-01-2007公路斜拉桥设计细则[S].北京：人民交通出版社，2007.

[10]中华人民共和国交通部. JTG/T D60-01-2004 公路桥梁抗风设计规范[S].北京:人民交通出版社,2004.

StudyonLimitationSpanofSelf-anchoredExtradosedCable-stayedBridge

PengYi1,SongTao2,ShengMan1，JiangJiao1

(1.Tianmen Building Quality Surveillance, Tianmen 473000, China; 2.Technology Center of .Second Harbor Engineering Co. Ltd ., CCCC. , Wuhan 430040, China)

The limit span of self-anchored concrete extrodosed cable-stayed bridge is discussed from the deformation and stress of main girder, the strength of the cable, the buckling stability , and anti-windy stability under the current condition of technology. The results show that the buckling stability is the main factor to limit the increase of extrodosed cable stayed bridge span; girder stress under dead and live load is secondary factor; while the girder deformation , cable strength, and anti-windy stability have little effect on the limitation span of extradosed cable stayed bridge. The primary problem of increasing extrodosed cable stayed bridge span is to improve the structural buckling stability. The result can be applied to selecting rational structural parameter for the extradosed cable stayed bridge with double-towers while the tower is rigidly connected with the girder and supported by the pier.

bridge engineering;extradosed cable-stayed bridge;limitation span;buckling stability

U448.25

A

2095-0373(2017)04-0006-07

2016-09-19责任编辑车轩玉

10.13319/j.cnki.sjztddxxbzrb.2017.04.02

国家科技支撑计划(2011BAG07B03)

彭义(1989-),女,助理工程师, 主要从事桥梁与隧道工程研究。E-mail:761282698@qq.com

彭义,宋涛，盛曼，等.自锚式预应力混凝土矮塔斜拉桥的力学极限跨径研究[J].石家庄铁道大学学报:自然科学版,2017,30(4):6-11.