山区地下开采地表移动变形分析

， ， ， ， ，

(1.中铁三局集团 第二工程有限公司，河北 石家庄 050031；2.石家庄铁道大学 工程力学系，河北 石家庄 050043；3.石家庄铁道大学 土木工程学院，河北 石家庄 050043)

山区地下开采地表移动变形分析

张玉根1，安延伟1，王永彬1，闻磊2，袁维3，王伟3

(1.中铁三局集团 第二工程有限公司，河北 石家庄 050031；2.石家庄铁道大学 工程力学系，河北 石家庄 050043；3.石家庄铁道大学 土木工程学院，河北 石家庄 050043)

地下开采引起的地表移动变形可对地表建(构)筑物产生损坏，地下开挖地表移动变形分析对地表建(构)筑物的安全评价有着重要的实际应用价值。利用概率积分法推导出山区地表移动变形的数学模型，分析山区地下开采地表移动变形特性，利用该数学模型对具体工程实例进行分析。研究结果表明：地表自然坡坡角不同时，最大水平拉伸变形不同，随着坡度的增加，最大水平拉伸变形减小；在靠近山脚处水平变形较大，水平移动系数对地表的水平变形影响显著。该数学模型可很好地分析山区地下开采地表移动变形，为矿区地表建(构)筑物的设计和施工提供了可靠的分析方法。

地下开采；地表移动变形；山区；概率积分法

0 引言

如今，岩层移动变形研究有了许多新的发展，地下开采引起的地面下沉和移动变形问题也有了较为成熟的分析方法[1-6]。谭志祥等[7]在实测资料基础上，通过理论分析获得了下沉系数与采宽的关系式以及水平移动系数、主要影响范围角、拐点偏移距与宽深比的关系式。秋兴国等[8]采用计算机可视化手段得到了一种用于任意形状采煤工作面开采后地面沉陷变形预测系统。胡海峰等[9]结合高速公路实例，得出残余变形预测与计算方法。目前，基于概率积分法对矿山开采地表移动变形进行分析是公认的方法，概率积分法被引入到《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程》(煤行管字[2000]第81号)(以下简称“三下规程”)中，作为煤矿开采地表移动变形的最主要方法，由于非煤矿山缺乏类似“三下规程”的行业规范，因此非煤矿山开采地表移动变形计算也普遍借鉴“三下规程”中的概率积分法。随着现代化手段的进步和计算机性能的飞速发展，地下开采岩层移动变形正趋于电算化和可视化发展，但地下开采地表移动变形理论研究对地表地形因素考虑较少，当研究对象满足平面应变条件，可以采用二维概率积分法分析时，目前能够考虑地形因素的二位概率积分法公式推导极少，山区地下开采地表移动变形缺少理论基础。随着采矿业的发展，人们越来越多的开发高陡山区的矿产资源，不仅对山体稳定产生了重大影响，而且势必对矿区附近地表设施产生危害。山区地下开采地表移动变形基础理论研究是必要的，山区地表移动变形数学模型的建立可很好地分析山区地下开采地表移动变形特征，为矿区地表建(构)筑物的设计和施工提供可靠的分析方法，具有重要的实际应用价值。

1 山区地下开采地表移动变形数学模型

假设被采动岩体为随机介质，在水平矿层单元开采的影响下，山区地表形成了单元下沉盆地，单元下沉盆地累积组成地表下沉盆地，如图1所示。

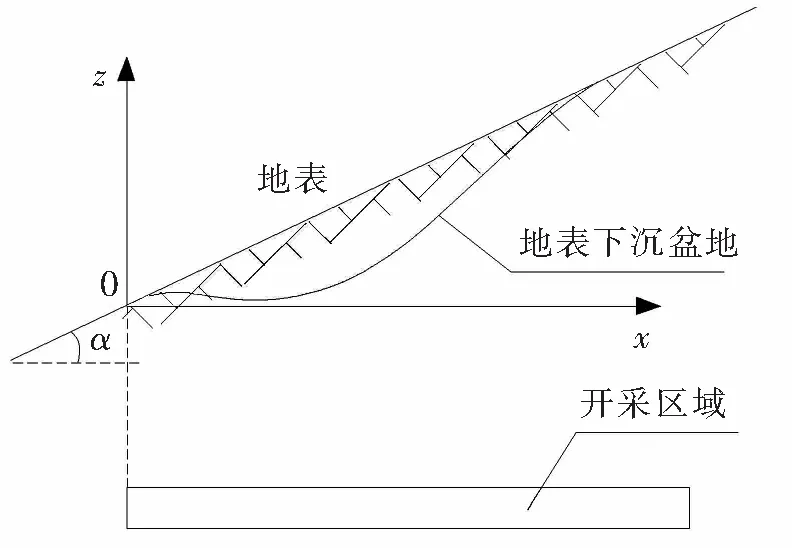
图1 山区地表下沉盆地示意图

地下各单元开采对地表点的影响称为影响函数，可采用式(1)的形式表示。

式中，h，P为待定参数；x为开采单元坐标值。

开采对地表总的影响等于地下各点开采影响的叠加，对于厚度均一的水平矿层，地表任一点的下沉表达式为

式中，-s0，s0为井下开采所划分微元的起始边界；Wmax为最大下沉值；r(x,z)为主要影响半径。

主要影响半径随地表点的位置而变化是山区地表移动规律的最大特点。山地各地表点所对应的主要影响半径r(x,z)为

因此，山地地表下沉计算公式可表示成

式中，L为开采宽度；k为下沉系数；m为开采厚度；H为最大开采深度；β为主要影响范围角；α为山地地表自然坡的坡角。

由此可得，采区上部地表岩层水平移动计算公式为

式中，b1为水平移动系数，其他符号意义同前。

地表水平变形表达式可由式(4)导出，其表达式为

本文山区地下开采地表移动变形数学模型属于平面问题研究范畴，矿体开采形态需满足平面问题假设，该数学模型的应用前提是被采动岩体可视为随机介质且符合概率积分法应用条件。

2 数学模型应用分析

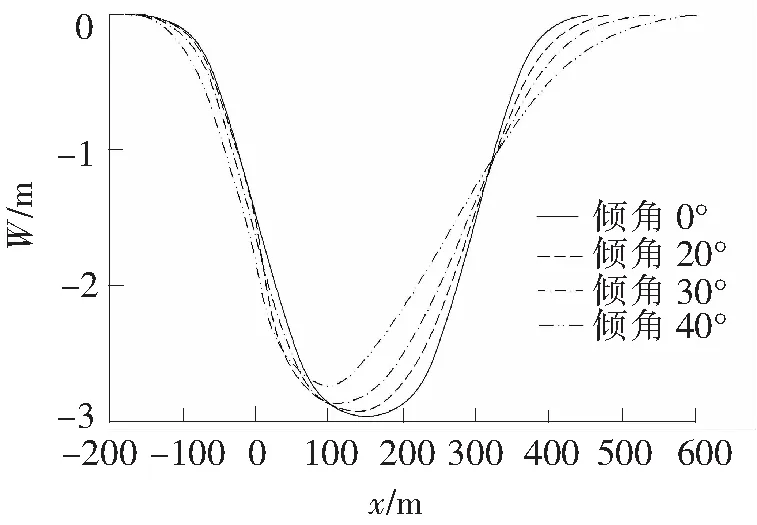
图2 地表下沉曲线

某矿区位于丘陵地带，地表高低起伏，下部矿层厚度为10 m，开采范围宽度为300 m，采用长臂法开采，冒落法管理顶板，上覆岩层为近水平状沉积岩，为中等坚硬岩石，最大开采深度H为400 m，适合采用概率积分法进行地表移动变形分析。根据现有的资料，结合“三下规程”相关规定，采用工程类比法获得地表移动计算参数为：主要影响范围角β=70°；下沉系数k=0.3。

2.1 不同自然坡脚地段地表变形分析

按坡角α分别取0°、20°、40°、60°时考虑，取水平移动系数为b1=0.25。

根据地表移动参数值，利用推导出的数学模型进行计算分析，得出不同自然边坡角对应的地表下沉曲线、地表水平移动曲线、水平变形曲线分别见图2～图4，地表不同位置水平移动、水平变形值见表1、表2。

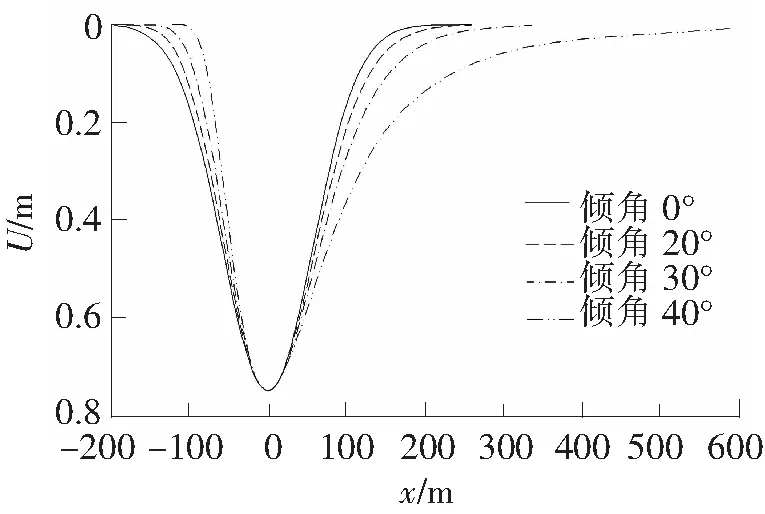
图3 地表水平移动曲线

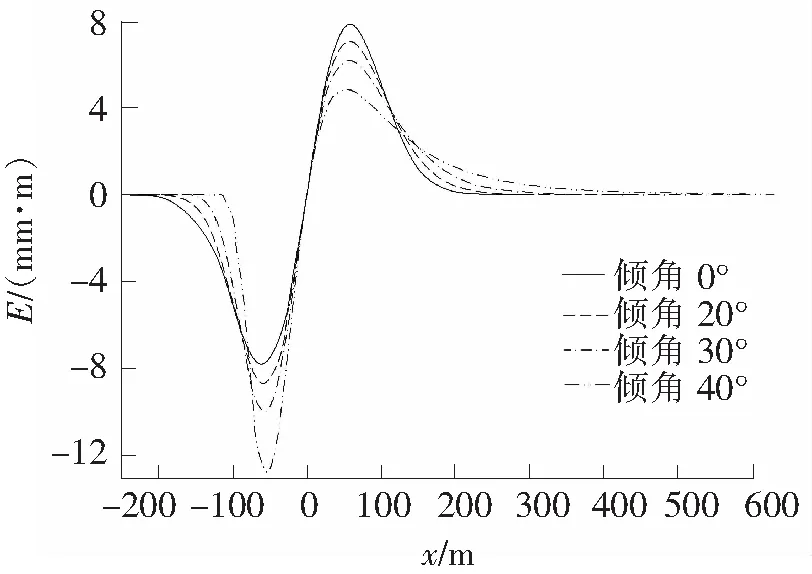
图4 地表水平变形曲线

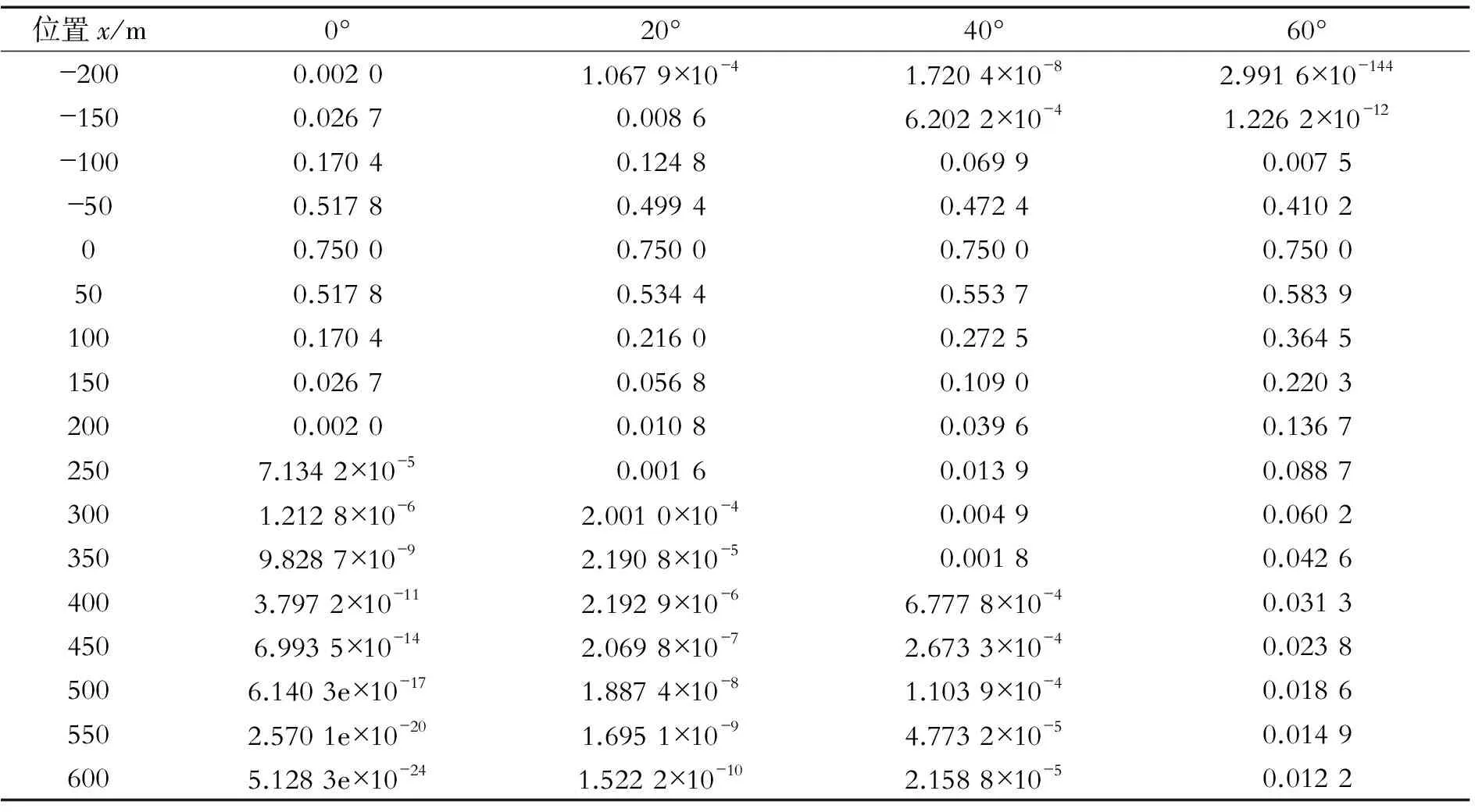
表1 α取不同角度时地表水平移动值 m

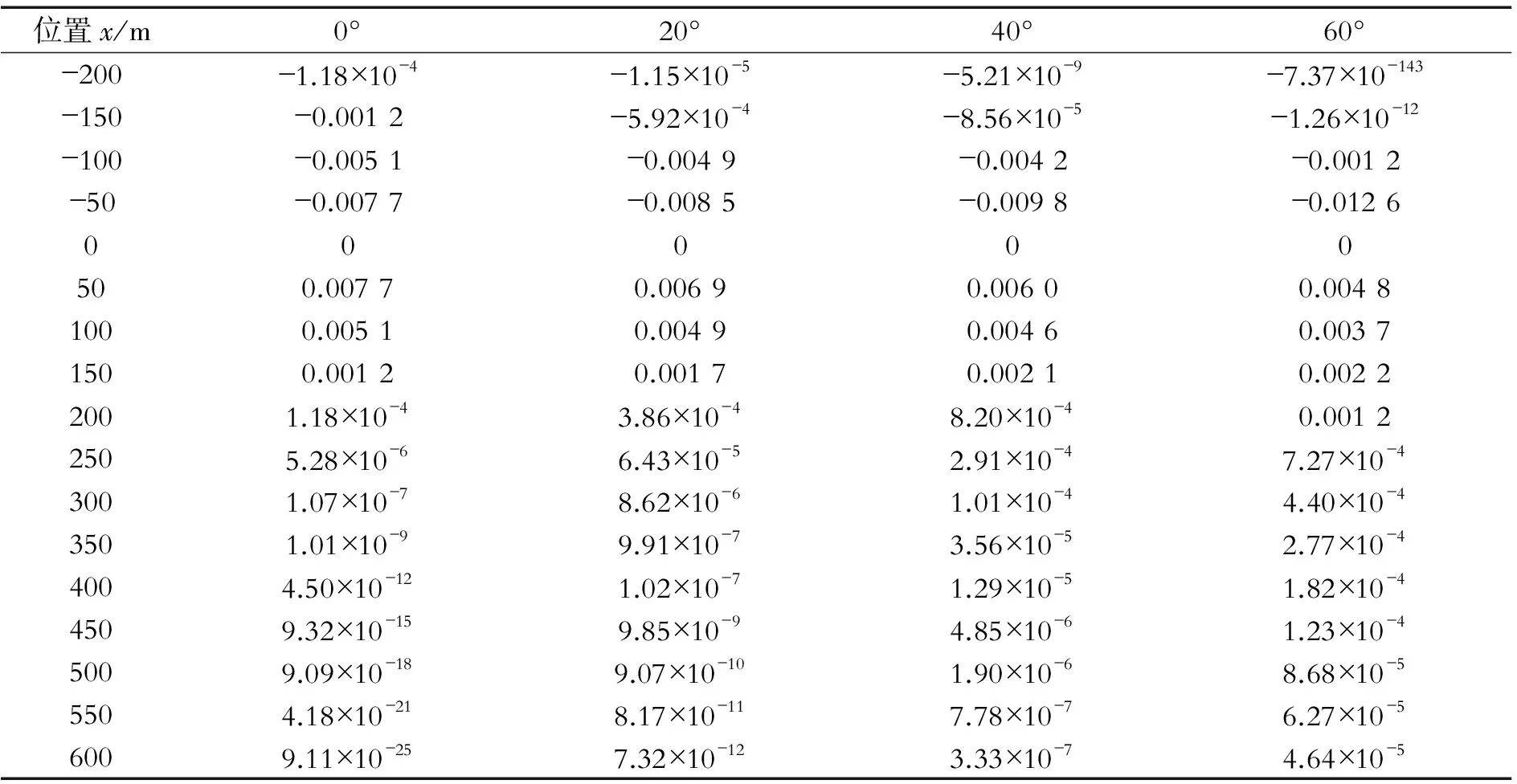
表2 α取不同的角度时地表水平变形 mm·m-1

由图4及表2可得，当边坡角α分别取0°、20°、40°、60°时，最大水平拉伸变形Emax分别为0.007 7，0.006 9，0.006 0，0.004 8。

随着边坡角α的增大，地表最大下沉值有所减小，最大下沉点偏向坡脚方向。水平移动系数确定时，随着边坡角α的增大，水平移动最大值相同，水平移动影响范围在坡顶方向影响更远，而坡脚方向影响范围更近。地表自然坡坡角不同时，最大水平拉伸变形不同，随着坡度的增加，最大水平拉伸变形有所减小。

2.2 水平移动系数对地表变形影响分析

当边坡角α=0°，水平移动系数b1分别取0.1，0.2，0.3时，地表水平移动见图5。当α=40°，水平移动系数b1分别取0.1，0.2，0.3时，地表水平移动见图6。

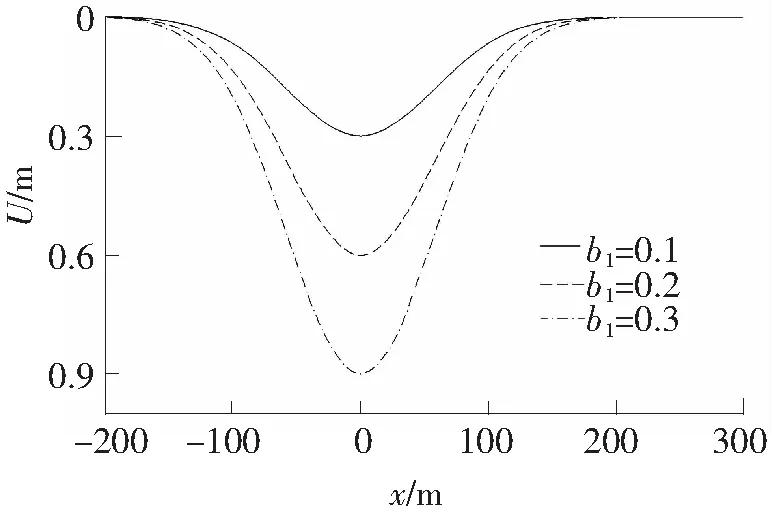
图5 地表水平移动曲线(α=0°)

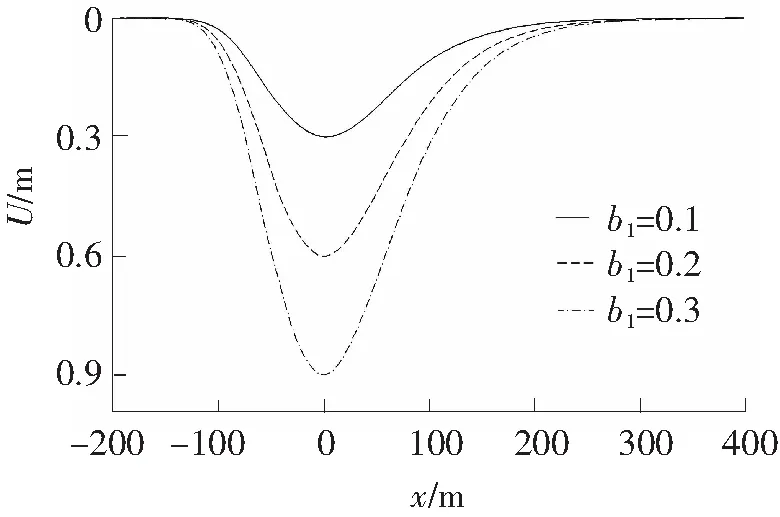
图6 地表水平移动曲线(α=40°)

由图5、图6可知，水平移动系数对山区地表的水平变形影响显著，随着水平移动系数的增大，地表水平移动最大值增加，但水平移动影响范围变化不大，最大水平变形发生在靠近山脚的地段。

3 结论

(1)利用概率积分法理论推导出的山区地表移动变形数学模型适用于山区地下开采地表移动变形分析，为矿区地表工程的设计和施工提供了可靠的计算方法。

(2)随着边坡角α的增大，地表最大下沉值有所减小，最大下沉点偏向坡脚方向。山地边坡角α不同时，最大水平拉伸变形不同，随着坡度的增加，最大水平拉伸变形有所减小。

(3)山区地表水平移动较大，最大水平变形发生在靠近山脚处，水平移动系数对地表的水平变形影响显著。

[1]颜荣贵. 地基开采沉陷及其地表建筑[M]. 北京：冶金工业出版社，1995.

[2]刘宝琛，廖国华. 煤矿地表移动的基本规律[M]. 北京：中国工业出版社，1965.

[3]李文秀，赵胜涛. 宜昌磷矿地下开采岩体移动分析[J]. 岩土力学，2006，27(1)：137-140.

[4]闻磊. 地下开挖地表移动变形可视化系统开发[J]. 金属矿山，2010，10：126-128.

[5]任伟中，白世伟，葛修润. 厚覆盖层条件下采矿引起的地表变形陷落特征模型试验研究[J]. 岩石力学与工程学报，2004，23(10)：1715-1719.

[6]张雪峰， 王延兵， 陈英鹏，等. 浅埋小净距隧道下穿多股铁路的风险分析及对策[J].石家庄铁道大学学报：自然科学版，2015，28(3):49-55.

[7]谭志祥，邓喀中. 综放面地表变形预计参数综合分析及应用研究[J]. 岩石力学与工程学报，2007，26(5)：1041-1047.

[8]秋兴国， 刁瑞朋， 龚尚福. “三下”采煤地表变形预计系统的开发及应用[J]. 工矿自动化，2008，5：4-8.

[9]胡海峰，赵阳升，康建荣，等. 煤矿采空区跨度和延续时间与地面残余变形的相关规律及实证[J]. 岩石力学与工程学报，2008，27(1)：65-71.

StudyofSurfaceDeformationDuetoUndergroundMininginMountainAreas

ZhangYugen1，AnYanwei1，WangYongbin1，WenLei2，YuanWei3，WangWei3

(1.The 2nd Engineering Co. Ltd., China Railway 3rd Bureau Group，Shijiazhuang 050031，China；2.Mechanics Engineering Department，Shijiazhuang Tiedao University，Shijiazhuang 050043，China；3.School of Civil Engineering，Shijiazhuang Tiedao University，Shijiazhuang 050043，China)

The buildings and structures could be damaged by the surface movement due to underground mining. The analysis of geotechnical deformation due to underground mining is very useful for design and construction of the buildings. The mathematical models for analysis of surface movement due to underground mining in mountain areas are given using probability integration method. This model can be used for analysis of surface displacement and can get theoretical analysis results. The results show that the maximum horizontal tensile deformation decreases with the slope increase. Horizontal deformation is larger near the foothills. The model can be a novel approach to evaluating the deformation due to underground mining in mountain areas, and can be used for design and construction of surface structures in these areas.

mining engineering；rock displacement and deformation；mountain areas； probability integration method

TD26

A

2095-0373(2017)04-0031-05

2016-08-07责任编辑车轩玉

10.13319/j.cnki.sjztddxxbzrb.2017.04.06

张玉根(1973-)，男，高级工程师，主要从事铁道工程方面的研究。E-mail: zhangyugen1@163.com

张玉根，安延伟，王永彬，等.山区地下开采地表移动变形分析[J].石家庄铁道大学学报:自然科学版,2017,30(4):31-35.