玛纳斯河出山口径流EEMD-ARIMA预测

2017-12-18刘艳宋秋宇

水土保持研究 2017年6期

刘艳, 杨耘, 聂磊, 宋秋宇

(1.中国气象局乌鲁木齐沙漠气象研究所, 乌鲁木齐 830002;2.中亚大气科学研究中心, 乌鲁木齐 830002; 3.长安大学地质工程与测绘学院, 西安 710054;4武汉大学测绘遥感信息工程国家重点实验室, 武汉430079;5 新疆维吾尔自治区气象局, 乌鲁木齐 830002)

刘艳1,2, 杨耘3, 聂磊4, 宋秋宇5

定量估算暖湿化背景下干旱内陆河径流变化尤其是非线性变化和未来发展趋势对区域水资源配置具有指导意义。以干旱区典型流域——玛纳斯河流域流量最大的玛纳斯河为例，运用曼—肯德尔(Mann-Kendal1)，集合经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)和自回归积分滑动平均模型(Autoregressive Integrated Moving Average Model，ARIMA)多种方法对出山口水文控制站肯斯瓦特1957—2012年年均径流进行了分析，得到年均径流非线性和多年代趋势定量特征。结果表明：1957—2012年年均径流显著增加；经EEMD分解后获取年均径流时间序列4个模态IMF分量和一个趋势项，各模态中心频率不一样，表明年均径流存在多种周期规律。将表征多年代际震荡的IMF分量引入ARIMA预测年均径流，预测精度明显高于直接应用年均径流的ARIMA预测精度，这表明EEMD-ARIMA组合径流预测法对短期径流预测具有一定参考价值。

径流变化; 非线性变化; 演变; 水文控制站

玛纳斯河作为天山北麓流入准噶尔盆地流量最大的河流倍受关注，关于径流的研究主要集中在以下几个方面，一是近50 a玛纳斯河流域流量变化对气候变化的响应研究，南峰[1]，徐素宁[2]，唐湘玲[3]，姜亮亮[4]等指出流量与夏季气温和降水相关密切；陈伏龙等[5]发现肯斯瓦特水文站径流量、降水量和蒸发量存在线性相关并呈一致性增加趋势；凌红波[6]利用径流量年内分配特征指数指出54a来玛纳斯河径流量年内分配集中程度逐渐增强，同时最大径流出现时间有所提前。二是玛纳斯河流域流量多尺度分析，主要采用Morlet小波函数以获取主周期和主要次周期特征，判定结果上存在差异。沈雪峰等[6]指出玛纳斯河年径流存在7 a和25 a的主周期、凌红波等[7]指出年径流变化主周期分别为15 a，18 a和22 a，18 a为第一主周期、张伟等[8]指出径流变化第1主周期为27 a，第2～5主周期依次为16 a，20 a，9 a和2 a、吉磊等[9]指出第1主周期为32 a左右，第2主周期为10 a，第3～5主周期依次为17 a，2 a和6 a。三是基于模型的流域流量模拟，李慧等[10]运用SWAT实现了流域山区日径流模拟，为研究雪冰融水河流径流模拟提供了有效途径，李文倩等[11])基于TOPMODEL模拟了流域日降雨径流过程。已有研究表明，EMD/EEMD比小波分析法具有更强的局部表现能力，在处理非平稳、非线性信号时是一种更有效方法[12-16]，水文时间序列(暴雨、洪水、径流等)是典型的非平稳、非线性时间序列。因此，本文运用EEMD从径流时间序列中提取径流信号中各个尺度的变化，对玛纳斯河流域近50 a年均径流进行多尺度分析，以揭示不同时间尺度的振荡模态结构特征，探究过去50多年来径流变化由哪些时间尺度的振荡变化构成，这些不同尺度的振荡变化有何演变特征，各尺度的振荡对径流变化的贡献如何，哪些尺度的振荡是显著的或非显著，在不同时期内各个尺度的振荡对整个气候变化起何作用？在EEMD分解获取平稳IMF分量的基础上，组合EEMD-ARIMA预测模型，定量评估全球气候暖湿化背景下，径流变化趋势尤其是非线性发展趋势，更好地预测水资源未来变化方向，对区域水资源合理配置和生态可持续发展具有指导意义。

1 研究区概况

玛纳斯河流域呈南高北低走势，源头海拔5 000～5 500 m，拥有现代冰川，流域内冰川面积占天山北坡冰川面积的32%，另有少量森林和高山草甸。在天山山地中山区和前山区汇合了众多支流，至前山肯斯瓦特水文站流出山区进入山前平原，海拔高度随之降到500 m左右，山地垂直地带性特征十分明显，冬季降水(12—3月)以积雪形式储蓄在天山北坡中低山一带，到了夏季(6—8月)主要融水进入河槽，使得该流域河流具有明显的夏汛特点。

2 数据来源

玛纳斯河上游布设红沟煤窑、清水河子、肯斯瓦特和红山嘴站4个水文要素观测站，其中肯斯瓦特是玛纳斯河干、支流汇合后的出山口控制站，海拔910 m，控制面积约4 926 km2。所用肯斯瓦特水文站径流数据来自石河子水文局，观测周期1957—2012年，观测步长为日，数据单位m3/s。由每日径流数据计算取得年均流量，用于趋势分析和突变检验。年均径流进行归一化后进行EEMD分解，获取尺度信息。

3 研究方法

3.1 径流序列集合经验模态分解法(EEMD)多尺度分解

3.2 径流序列变异诊断方法及趋势分析

采用世界气象组织推荐的曼—肯德尔(Mann-Kendal1)非参数统计检验法对年均径流量序列进行趋势分析和突变检验。Mann-Kendall法是一种非参数统计检验方法，不需要样本遵从一定的分布，也不受少数异常值的干扰，计算简单且结果易于分析[20]。分析绘出顺序/逆序统计量曲线UFk/UBk，若UFk>0或UBk>0，表明序列呈上升趋势；若UFk<0或UBk<0，表明呈下降趋势；若UFk或UBk的值超过临界线，表明上升或下降趋势显著；若UFk和UBk曲线出现交点且交点位于临界线之间，交点对应时刻即为突变开始时间。

3.3 ARIMA-EEMD径流预测模型及精度检验

自回归积分滑动平均模型(Autoregressive Integrated Moving Average Model,ARIMA)指将非平稳时间序列转化为平稳时间序列后因变量仅对它的滞后值和随机误差项现值和滞后值进行回归建立的模型[21]。ARIMA模型表示为：

(1)

φp≠0，θp≠0

(2)

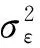
(3)

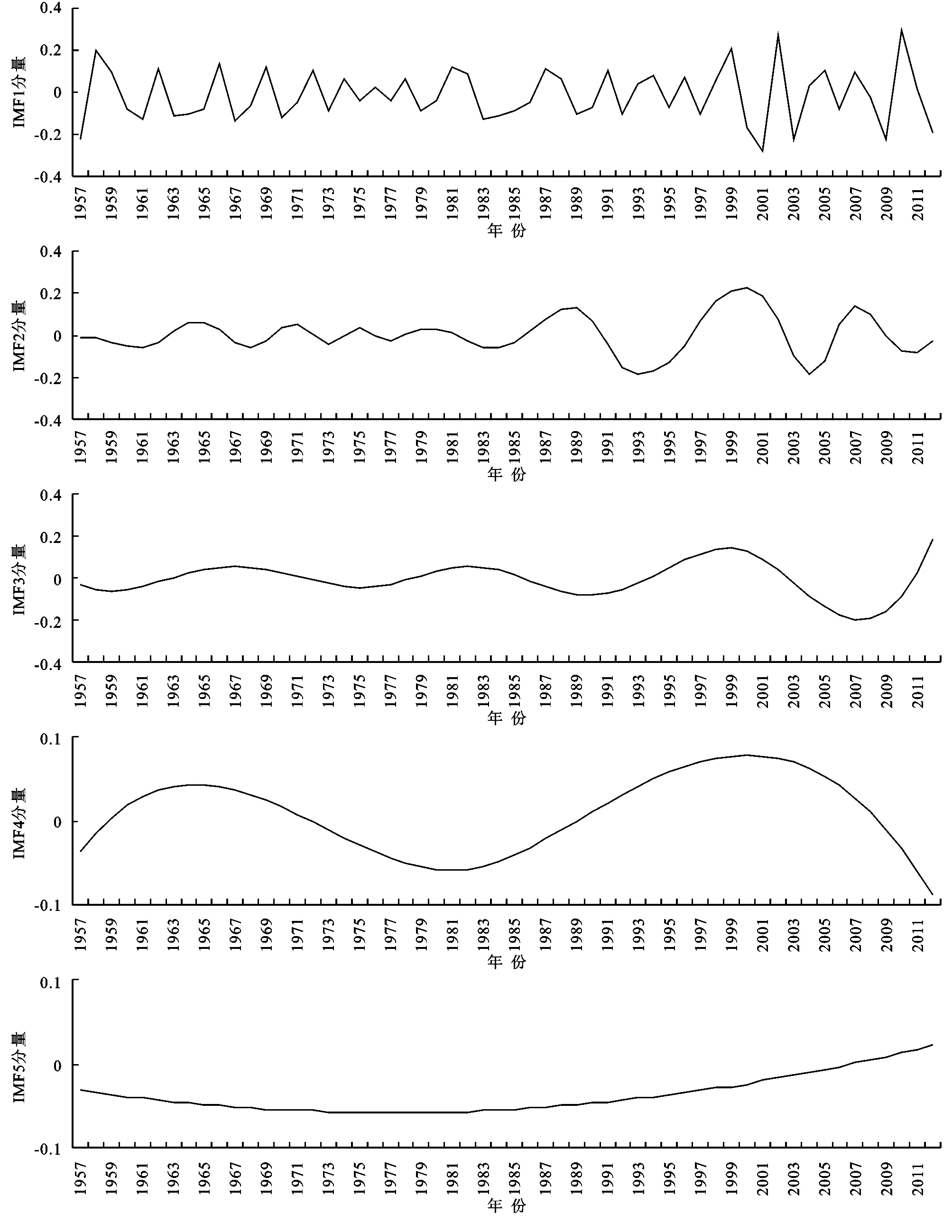
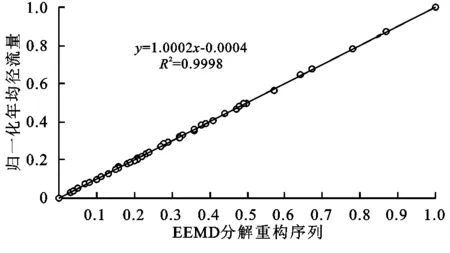
Exsεt=0,∀s

(4)

式中：L是滞后算子。ARIMA根据原序列是否平稳及回归中所含部分的不同，包括移动平均过程(Moving-Average，MA)表明误差序列能用其前面的q项白噪声序列的移动平均表出、自回归过程(Auto-Regression，AR)表明时间序列能用其前面的p项的回归表出、自回归移动平均过程(Auto Regressive Moving Average，ARMA)表明时间序列基本是平稳的，不用进行差分就可以拟合和ARIMA过程(Box et al.1994)表明时间序列的d阶差分能满足ARMA(p，q)模型。基于EEMD实现肯斯瓦特年均径流时间序列高频到低频的分解，得到表征多年代际震荡的本征模态函数(IMF分量)和趋势项(Res分量)，将IMF分量引入ARIMA对年均径流进行各分量的趋势预测[22-25]。径流数据分为模型调试阶段(1957—2005年)验证阶段(2006—2012年)和预测阶段(2013—2020年)，采用均方根误差(Root mean square error，RMSE)[26]，相对百分误差(Mean absolute relative error,MARE)[27]，纳什效率系数(Nash-Sutcliffe efficiency coefficient,NSEC)[28]和模型决定系数(Coefficient of correlation,R)[29,30]4类指标对模型精度进行定量评估。具体公式如下：

(5)

(6)

(7)

(8)

4 结果与分析

4.1 径流量Mann-Kendall特征分析

肯斯瓦特水文站年均径流的Mann-Kendall统计量Zc=2.650 59，p-value=0.0040176，alpha=0.05，表明年均径流显著增加。非参数检验只是考察了整个时间序列的变化趋势，对河流径流而言，突变指时间序列在某时刻发生急剧变化的一种形式，表现为突变点前后平均河流径流量发生陡升或陡降(图1)。

图1肯斯瓦特水文站1957-2012年年均径流Mann-Kendall统计量曲线

采用Mann-Kendall法对肯斯瓦特水文站年均径流序列进行突变检验(图1)，设置信水平a=0.05，查正态分布表得临界值U0.05/2=1.96。检验结果显示：(1) 除去1961年、1975—1997年，肯斯瓦特水文站年均径流的UFk统计值为正值表示期间径流呈上升趋势。其中，2007—2012年统计值超过显著性水平0.05，突破了95%的置信区间，统计量绝对值超过了2.038 6，显示近年来年均径流有十分显著的上升趋势。(2) 1975—1997年UFk统计值为负值切在95%的置信区间内，表示这段时间内年均径流呈下降趋势但趋势不明显。(3) 由UFk与UBk曲线交点所在位置可以确定年均径流的突变时段。由图1可见，1996年UFk与UBk两条曲线出现相交，突变点在置信区间内，即拒绝无突变的原假设或突变成分显著，随后UFk曲线在2007年突破了95%的置信区间，说明年均径流的突变时段发生在1996年。(4) 由年均径流统计值(图2)，1957—1996年径流量年平均值是37.21 m3/s，1996—2012年径流量多年平均值是46.675 m3/s。可见，1996年的突变是年均径流量由低值向高值跳跃。

图2肯斯瓦特水文站1957-2012年年均径流曲线

4.2 集合经验模态分解下径流时间尺度分解

运用EEMD对年均径流数据进行多时间尺度分解，白噪声标准差取ε=0.4，n=200，年均径流序列被自适应分解为频率和周期不同的4个本征模态函数(IMF分量)和一个趋势项Res分量(图3)。各IMF分量依次反映了从高频到低频不同时间尺度的波动特征，周期不同的IMF代表不同周期影响年径流走势的分量，趋势项表示原数据总体随时间变化的趋势，体现了影响年径流的长期内在趋势。为验证分解结果的可靠性，分解得到的IMF1，IMF2，IMF3，IMF4和Res趋势项依次相加得到1个重构序列(图6)，发现重构序列与原始径流序列基本吻合，重构序列很好地恢复了原始序列中的各种状态，由此说明EEMD分解具有较高的准确性，分解结果是可信的，可以利用分解结果进行预测。

分解得到的IMF相互独立，IMF方差比可以比较不同IMF对年均径流序列波动的贡献率，进而比较不同周期的IMF序列对年均径流序列波动的影响。表1给出了年均径流各分量的方差贡献率和平均周期。平均周期法定义如下：

(9)

式中：T为变化周期；N1为总体数据数；N2为极小值点或极大值点数。通过统计波峰和波谷的数量来计算年均径流的变化周期(表1)。

图3可见每个IMF分量信号波动具有相对稳定的准周期性，在相同的时段内不同时间尺度的准周期振荡随时间呈现或强或弱的非均匀变化，根据各IMF分量波动特点可以发现，IMF1-IMF4频率依次减小，周期依次变长，平均幅值依次变小。综合图3和表1，IMF1表示的准3 a周期贡献率最大，达到了34.96%，振荡信号极为明显，径流振幅呈现出增大—减小—增大趋势，1958年、1999年、2002年、2010年径流振幅明显高于其他时段；IMF2表示准8 a周期方差贡献率约为17.99%，20世纪80年代后期(1986—1991年)，90年代末期和2000年初(1996—2013年)径流振幅较其余时期偏大；IMF3分量表示的准18 a周期方差贡献率为12.40%，在1957—1986年这个时段内的振幅相对较小，1994—2003年处于偏多状态；IMF4分量表示的是径流准28 a的周期变化，其方差贡献率为5.02%，在此时间尺度上，径流在1972—1989年处于偏少状态；趋势项分量的方差贡献率高30.05%，1957—2012年期间径流整体上呈近似线性但实为非线性显著增多趋势。

一般情况下，每个IMF分量都具有物理意义，各自反映了原序列中固有的不同特征尺度的振荡。分解得到几个本征模函数(IMF)，怎样知道这些周期哪些是显著的，哪些是不显著的？可通过分析IMF能量谱密度—周期的分布关系判断其属性，即在以lnT—lnE为轴的平面直角坐标系中，白噪声的IMF应分布在斜率为-1的直线上[31]。图5横轴为IMF分量所对应的固有波长特征尺度的自然对数，越靠左的IMF分量，频率就越高，波长越小。纵轴为IMF分量所具有的能量谱密度的自然对数，越靠近上方的IMF分量，表示具有的能量越高，振幅越大。可见，IMF4处于95%～99%的置信区间，说明IMF4分量最为显著，包含的具有实际物理意义的信息最多，对应的振荡周期为径流序列的主要振荡周期。IMF2落在80%～90%的置信区间，所包含的具有实际物理意义的信息相对略少，对应的振荡周期为径流序列的第二振荡周期。IMF1和IMF3置信度较差，落在50%的置信区间之下，说明其包含的周期性振荡不显著。这一结果与沈雪峰等[7]应用Morlet小波和小波方差检验所得玛纳斯河年均径流存在7 a和25 a的主周期比较吻合。与张伟等[9]运用小波分析指出27 a左右为径流变化的第1周期最为吻合，但其指出径流存在2～5的主周期，依次为16 a，20 a，9 a和2 a。与凌红波[8]应用小波变换指出年径流变化的主周期分别为15 a，18 a和22 a，其中18 a为第一主周期的结果差异显著。与吉磊[9]指出32 a左右为第1主周期差异较大，10 a左右为第2周期的结果比较接近，但其指出径流存在3～5的主周期依次为17 a，2 a和6 a。这些研究说明，径流在演化过程中，并不存在真正意义上的变化周期，而是其变化周期随着研究尺度的不同而发生相应的变化，这种变化一般表现为小时间尺度的变化周期往往嵌套在大尺度的变化周期之中。也就是说，径流变化在时间域中存在多层次的时间尺度结构和局部变化特征。

图31957-2012年归一化年均径流各IMF分量及趋势项

图4 1957-2012年归一化年均径流及各IMF分量及趋势项重构径流序列

4.3 EEMD-ARIMA径流预测

4.3.1 时间序列的平稳化检验运用ARIMA建模前，首先需要对时间序列平稳性进行检验。本文采用ADF(Augmented Dickey-Fuller,ADF)单位根(unit root test)检验精确判断序列的平稳性[32]。对于非平稳时间序列，如果存在异方差，需要先对序列进行对数转换；如果时间序列存在一定变化趋势，需要对序列进行差分处理，使之转化为平稳的时间序列，此时差分次数即是ARIMA(p，d，q)阶数d。以年均径流为例，表4中ADF统计量为0.405 073，大于1%临界值(-2.614 029)，5%临界值(-1.947 816)，10%临界值(-1.612 492 6)表明存在单位根，年均径流序列不平稳。年均径流1阶差分数据的ADF统计量-4.557 321，小于1%临界值(-2.614 029)，拒绝单位根假设，表明年均径流经过一阶差分后序列平稳，ARIMA(p,d,q)中阶数d=1。ADF检验结果表明各IMF分量序列平稳，可直接应用ARIMA建模。

图5 各IMF分量趋势的显著性检验

注：h=1表示通过ADF检验；h=0表示未通过ADF检验。

4.3.2 IMF分量得ARIMA预测年均径流1阶差分数据序列已经平稳，对其应用ARIMA(p,d,q)进行预测，观察ACF从多少阶衰减确定q=2，观察PACF从多少阶衰减确定p=5；比较赤池信息准则(Akaike info criterion,AIC)和施瓦茨准则(Schwarz criterion,SC)的值，根据值越小，模型越适合的原则，优选ARIMA(p,d,q)，结果见表3。

4.3.3 Res分量回归拟合及预测利用最小二乘法对趋势项Res进行估计，回归拟合方程如下：Y=0.0003t2-1.2966t+1282 (R2=1)，式中t是对应年，Y是Res模拟值。

4.3.3 年均径流预测和精度分析根据所取得的径流序列数据，本文将年均径流数据和年均径流EEMD分解获取的各个IMF分量数据及趋势项Res分为3部分，其中1957—2005年实测径流数据用于EEMD-ARIMA和Runoff-ARIMA模型参数调试和应用(图6)，2006—2012年实测径流数据用于EEMD-ARIMA和Runoff-ARIMA径流预测结果的精度验证，在精度可信的基础上，应用EEMD-ARIMA和Runoff-ARIMA实现2012—2020年径流的预测(图7)。精度检验结果显示，集合EEMD-ARIMA径流预测精度检验R值为0.956，年均径流直接运用ARIMA的径流模拟精度R为0.344，根据R越大模拟精度越高的判识原则，EEMD-ARIMA模拟精度远远大于常规Runoff-ARIMA径流模拟精度。

预测结果表明，2013—2020年这段时间内，肯斯瓦特径流量将以较快的速度上升。这一预测结果与凌红波[7]运用周期性叠加趋势模型预测在从2012年的未来5 a玛纳斯河源流来水量将呈增加走势的结果是一致的。

表3 优选ARIMA(p,d,q)模型结果

注：ARIMA(p，d，q)AR是自回归；p为自回归项；MA为移动平均；q为移动平均项数；d为时间序列成为平稳时所做的差分次数。

图6 试验阶段(1957-2005)和检验阶段(2006-2012)年均径流预测

图7 EEMD-ARIMA和Res回归拟合值预测径流(2013-2020年)

5 结论

运用集合经验模态分解法(EEMD)肯斯瓦特水文站近55 a年均径流序列被分为4个模态(IMF)和1个趋势项(Res)，各模态中心频率不一样，表明年均径流存在多种周期规律，呈显著年际和年代际尺度振荡特征，通过显著性检验，年均径流主要表现为28 a左右的年代际变化和8 a左右的年际变化。各分量方差贡献率显示，年际振荡在径流长期变化中占据主导地位；综合已有径流周期特征的研究成果看[6-9]，径流在演化过程中并不存在真正意义上的变化周期，而是其变化周期随着研究尺度的不同而发生相应的变化，这种变化一般表现为小时间尺度的变化周期往往嵌套在大尺度的变化周期之中。也就是说，径流变化在时间域中存在多层次的时间尺度结构和局部变化特征。趋势项表明，自1957年以来肯斯瓦特水文站径流长期变化趋势表现为持续上升趋势。EEMD成功了实现了对肯斯瓦特水文站径流的时间序列进行从高频到低频的分解，EEMD有效的揭示了肯斯瓦特近55 a来径流长时序列在不同时间尺度上的变化规律，有效诊断了径流这一典型非线性、非平稳性信号变化的复杂性特征。EEMD分解获取的各个4个模态(IMF)均为平稳序列，自回归积分滑动平均模型(ARIMA)进行组合预测，发现EEMD-ARIMA组合预测可有效地提高径流的预测精度。

[1] 南峰,李有利,史兴民.新疆玛纳斯河水量波动与气候变化之间的关系[J].水土保持研究,2003,10(3):59-61.

[2] 徐素宁,杨景春,李有利.近50a来玛纳斯河流量变化及对气候变化的响应[J].地理与地理信息科学,2004,20(6):65-68.

[3] 唐湘玲,龙海丽,邢永建.玛纳斯河流域降水与径流变化及其人类活动的影响[J].新疆师范大学学报:自然科学版,2005,24(3):145-152.

[4] 党新成,李新贤,高建.玛纳斯河流域水文与环境特征分析[J].水文,2006,26(5):89-90.

[5] 凌红波,徐海量,张青青,等.新疆玛纳斯河年径流时序特征分析[J].中国沙漠,2011,31(6):1639-1646.

[6] 沈雪峰,艾成.新疆玛纳斯河径流时间变化特征及其趋势分析[J].干旱区资源与环境,2012,26(7):14-19.

[7] 凌红波,徐海量,张青青,等.新疆玛纳斯河径流过程的非线性特征[J].自然资源学报,2011,26(4):683-693.

[8] 张伟,何新林,刘兵,等.天山北麓玛纳斯河径流规律的分析[J].石河子大学学报:自然科学版,2008,26(1):80-82.

[9] 吉磊,何新林,刘兵,等.近60年玛纳斯河径流变化规律的分析[J].石河子大学学报:自然科学版,2013,31(6):765-769.

[10] 李慧,雷晓云,包安明,等.基于SWAT模型的山区日径流模拟:在玛纳斯河流域的应用[J].干旱区研究,2010,27(5):686-690.

[11] 李文倩,汤骅,薛联青.基于融雪TOPMODEL模型对玛纳斯河流域径流的模拟[J].石河子大学学报:自然科学版,2015,33(6):779-786.

[12] 冯平,丁志宏,韩瑞光.基于EMD的洮河年径流量变化多时间尺度分析[J].干旱区资源与环境,2008,22(12):73-76.

[13] 王兵,李晓东.基于EEMD分解的欧洲温度序列的多尺度分析[J].北京大学学报:自然科学版,2011,47(4):627-634.

[14] Ayenu-Prah A Y, Attoh-Okine N O. Comparative study of Hilbert-Huang transform, Fourier transform and wavelet transform in pavement profile analysis[J]. Vehicle System Dynamics, 2009,47(4):437-456.

[15] Alexandrov T. A method of trend extraction using singular spectrum analysis[J]. Revstat-Statistical Journal, 2009,7(1):1-22.

[16] Flandrin P, Rilling G, Gonçalves P. Empirical mode decomposition as a filter bank[J]. IEEE Signal Proc. Lett.,2004,11(2):112-114.

[17] Wu Z H, Huang N E. Ensemble empirical mode decomposition:a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009,1(1):1-41.

[18] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J]. Proceedings of the Royal of Society A,1998,454:903-995.

[19] Wu Z, Huang N E. Ensemble empirical mode decomposition:A noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009,1(1):1-41.

[20] 郭小芹,刘明春,钱莉,等.从Mann-Kendall特征看石羊河流域降水量的演变规律[J].干旱区地理,2010,33(4):593-599.

[21] Box G E P, Jenkins G M, Reinsel G C, et al. Time Series Analysis:Forecasting and Control[M]. John Wiley & Sons, 2015.

[22] Xu J Y， Chen L， Bai Y X. A hybrid model to simulate the annual runoff of Kaidu River in northwest China[J]. Hydrology & Earth System Sciences Discussions, 2016,20(4):1-33.

[23] Zhang G P. Time series forecasting using a hybrid ARIMA and neural network model[J]. Neurocomputing, 2003,50(1):159-175.

[24] Duan W Y, Huang L M, Han Y, et al. A hybrid EMD-AR model for nonlinear and non-stationary wave forecasting[J]. Journal of Zhejiang Universityence A,2016,17(2):115-129.

[25] Wang W C, Chau K W, Xu D W, et al. Improving Forecasting Accuracy of Annual Runoff Time Series Using ARIMA Based on EEMD Decomposition[J]. Water Resources Management, 2015,29(8):2655-2675.

[26] Dawson C W, Abrahart R J, See L M. HydroTest:A web-based toolbox of evaluation metrics for the standardised assessment of hydrological forecasts [J]. Environmental Modelling & Software, 1995,22(7):1034-1052.

[27] Karunanithi N, Grenney W J, Whitley D, et al. Neural networks for river flow prediction[J]. Journal of computing in Civil Engineering, 1994,8(2):201-220.

[28] Nash J E, Sutcliffe J V. River flow forecasting through conceptual models. part I: A discussion of principles[J]. Journal of Hydrology, 1970,10(3):282-290.

[29] Legates D R, McCabe G J. Evaluating the use of‘goodness-of-fit’ measures in hydrologic and hydroclimatic model validation[J]. Water Resources Research, 1999,35(1):233-241.

[30] Wang W C, Chau K W, Cheng C T, et al. A comparison of performance of several artificial intelligence methods for forecasting monthly discharge time series[J]. Journal of Hydrology, 2009,374(3):294-306.

[31] Wu Z, Huang N E. A study of the characteristics of white noise using the empirical mode decomposition method[C]∥Proceedings of the Royal Society of London A:Mathematical, Physical and Engineering Sciences. The Royal Society, 2004,460(2046):1597-1611.

[32] Adak S. Time-dependent spectral analysis of nonstationary time series[J]. Journal of the American Statistical Association, 1998,93(444):1488-1501.

TheEEMD-ARIMAPredictionofRunoffatMountainPassofManasRiver

LIU Yan1,2, Yangyun3, NIE Lei4, SONG Qiuyu5

(1.InstituteofDesertMeteorology,CMA,Urumqi830002,China; 2.CenterofCentralAsiaAtmosphericScienceResearch,Urumqi830002,China; 3.CollegeofGeologyEngineeringandGeomatics,Chang′anUniversity,Xi′an710054,China; 4.StateKeyLaboratoryofInformationEngineeringinSurveying,MappingandRemoteSensing,WuhanUniversity,Wuhan430079,China; 5.XinjiangUygurMeteorologicalBureau,Urumqi830002,China)

Quantitative estimation under warm-humid climate of the runoff variation of arid endorheic river, especially the nonlinear variation, and its trend in the future has directive significance for disposing regional water resources. Taking Manas River estimation under warm-humid climate of the runoff variati Manas Basin for example, in this context, we analyzed the annual average runoff data from 1957 to 2012 of mountain-pass hydrological station Ken Swart by using diversiform algorithms such as Mann-Kendall, Ensemble Empirical Mode Decomposition ( EEMD) and Autoregressive Integrated Moving Average Model (ARIMA), then ultimately got the quantitative characteristic of the nonlinear variation of annual average runoff and the trend between years. The results indicated that the annual average and general stream flow increased significantly. After decomposing through EEMD, we obtained 4 IMF components and 1 trend term of the time series of annual average runoff which differed from each other in central frequency, showing that there are varieties of periodic laws of annual average runoff. Introducing the IMF components representing years of intergenerational oscillation into ARIMA to predict annual average runoff, comparing with straightly using ARIMA to predict, we found that its result was more accurate, showing that using EEMD-ARIMA to predict short-term runoff could be positively valuable.

change of runoff; nonlinear variation; evolution; hydrological station

P96

1005-3409(2017)06-0273-08

2016-09-18

2016-10-31

国家自然基金(41471358,41301386)；风云三号(02)批气象卫星地面应用系统工程应用示范系统项目(FY-3(02)-UDS-1.5.1,FY-3(02)-UDS-1.5.3)

刘艳(1978—),女,河南省扶沟县,副研究员,硕士,主要从事遥感在积雪、植被变化监测等方面的研究。E-mail：liuyan@idm.cn